Cím: 1954. évi Kürschák József matematikai tanulóverseny feladatainak megoldása
Szerző(k):  Hajós György 
Füzet: 1955/április, 100 - 105. oldal  PDF  |  MathML 
Témakör(ök): Kürschák József (korábban Eötvös Loránd)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Első feladat. Az ABCD konvex négyszögben AB+BD nem nagyobb, mint AC+CD. Bizonyítandó, hogy akkor az AB oldal kisebb az AC átlónál.

 

Megjegyzések: 1. Mivel a feladat négyszögről szól, az A, B, C, D pontoknak egymástól különbözőknek kell lenniök. Ezért téved, aki szerint a feladatnak azt kellene állítania, hogy az AB oldal nem nagyobb az AC átlónál, hiszen AB=AC, ha B és C egybeesik (?).
2. A következő okoskodás alátámasztja azt, hogy a feladat állítása helyes. Rajzoljunk ellipszist, amelynek fókuszai A és D, és amelyik áthalad a B ponton (1. ábra).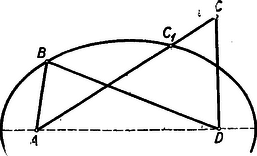
 
 
1. ábra
 

A feladat feltevéséből következik, hogy C ezen az ellipszisen kívül van, vagy esetleg rajta. Ezért az AC szakasznak egy C1 pontja az ellipszisen van, C1 esetleg azonos a C ponttal. Minthogy >>az ellipszisnek A-ból induló rádiuszvektora állandóan növekszik, amint végpontja az ellipszisen a nagytengely A-hoz közelebb eső végpontjától a D-hez közelebb eső végpont felé mozog<<, következik az, hogy AB kisebb AC1-nél, s így még inkább kisebb AC-nél. ‐ Ezt az okoskodást bizonyításnak nem nevezhetjük, hiszen az idézőjelek közé foglalt állítást a szemlélet alapján elhisszük ugyan, de bizonyítva nem látjuk. ‐ Bizonyítássá válik ez az okoskodás, ha ezt az állítást nemcsak kimondjuk, hanem bizonyítjuk is. Ennek kifogástalan elvégzése azonban elég körülményes feladat (hacsak nem éppen feladatunknak más megoldása alapján következtetünk ennek az állításnak helyességére). ‐ Az említett bizonyítás kevés munkával elvégezhető, ha a trigonometriát használjuk, és arra az előismeretre építünk, hogy pl. a cosinus-függvény 0∘ és 180∘ között állandóan fogy. Az ilyen bizonyítás eleminek és ötletesnek semmiképpen sem volna nevezhető.
 

I. megoldás. Tegyük fel, hogy állításunkkal ellentétben AB≥AC, hogy tehát az A pont a BC szakasz felezőmerőlegesén, vagy pedig ennek C felőli oldalán helyezkedik el (2. ábra).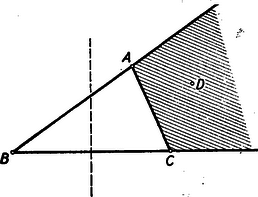
 
 
2. ábra
 

Mivel az ABCD négyszög konvex, következik, hogy a D pont az AB oldalegyenesnek C felőli oldalán, a BC oldalegyenesnek A felőli oldalán, végül az AC átlóegyenesnek B-vel átellenes oldalán van. A D pont tehát annak (az ábrán vonalkázott) tartománynak belsejében van, amelyet megkapunk, ha az ABC∢ tartományából az ABC háromszöget levágjuk. Ennek a tartománynak a belseje azonban egészben a BC szakasz felezőmerőlegesének C felőli oldalán van, hiszen határvonalainak pontjai közül legfeljebb csak A lehet a felezőmerőlegesen. Ezért a D pont is ebben a félsíkban van, és BD>CD. Ezt az egyenlőtlenséget az igaznak elfogadott egyenlőtlenséggel összegezve AB+BD> >AC+CD adódik, ami ellentmond a feladat kirovásának. Ez az ellentmondás feltevésünk lehetetlenségét és a feladat állításának helyességét bizonyítja.
 

II. megoldás. Ha BD>CD, akkor ebből és AB+BD≤AC+CD fennállásából (kivonással) következik, hogy AB<AC. Ezért a bizonyításnál jogosan szorítkozhatunk arra az esetre, amidőn BD≤CD (3. 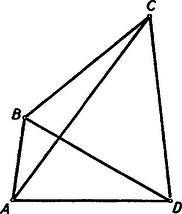ábra).
 
 
3. ábra
 

Ebben az esetben ‐ hivatkozva arra a tételre, hogy a háromszögben nagyobb oldallal szemben nagyobb szög van ‐ a BCD▵-ből adódik, hogy BCD∢≤DBC∢. Így tehát BCA∢<ABC∢, hiszen az előző egyenlőtlenség baloldalán szereplő szöget csökkentettük, a jobboldalon állót meg növeltük. Az utóbbi egyenlőtlenségből azonban ‐ a már idézett tételt az ABC▵-re alkalmazva ‐ adódik, hogy AB<AC.
 

III. megoldás. Ismeretes (és a háromszög oldalaira vonatkozó egyenlőtlenségből nyomban következik), hogy egy konvex négyszög két átellenes oldalának összege az átlók összegénél kisebb, esetünkben tehát AB+CD<AC+BD. A feladat feltevése szerint AB+BD≤AC+CD. Ezeket az egyenlőtlenségeket összegezve, rendezés után 2⋅AB<2⋅AC adódik, ami állításunkat bizonyítja.
 

Második feladat. Bizonyítandó, hogy ha egy test minden síkmetszete kör, akkor a test gömb.
 

Megjegyzések: 1. Legrövidebben a következő módon indokolhatjuk az állítás helyességét: Tekintsük a testnek egy leghosszabb húrját. E húron átfektetett sík körben metsz, s a húr ennek a körnek átmérője, hiszen különben ennek a körnek, tehát magának a testnek is volna a kiszemeltnél hosszabb húrja. Ebből azonban az következik, hogy a test azonos avval a gömbbel, melynek egyik átmérője a kiszemelt húr. ‐ Ez az okoskodás hiányos, mert nem bizonyítja, hogy van leghosszabb húr. Okoskodásunk bizonyítássá válnék, ha ezt is bizonyítanók, ehhez azonban a felsőbb matematika eszközeinek használatára volna szükség.
2. A feladat szövegezése félreértésre nem ad lehetőséget. Felvethető mégis a kérdés, mit jelent a >>test<< szó a szövegben. Felelhetjük, hogy térbeli pontoknak tetszőleges összességét, halmazát jelentheti. Feladatunknak ilyen irányban is szabatos megszövegezése így hangzik: Legyen egy térbeli ponthalmaznak egynél több pontja; rendelkezzék e ponthalmaz avval a tulajdonsággal, hogy ha egy síkban egynél több pontja van, akkor e síkban levő pontjai egy körlemezt (egy kör belső és határpontjai által alkotott halmazt) alkotnak; bizonyítandó, hogy e térbeli ponthalmaz gömb (egy gömb belső és határpontjainak halmaza). A következő megoldások akkor is hiánytalanok, ha azokat e szabatosabb feladatszövegezés szemüvegén át tekintjük.
I. megoldás. Tekintsük testünknek két párhuzamos síkmetszetét. Ezeknek középpontjain át síkjaikra merőleges síkot fektetünk. E sík a két kört négy pontban metszi (4. ábra).
 
 
4. ábra
 

E négy pont által meghatározott trapéz húrnégyszög, hiszen síkja a testet körben metszi; ezért e trapéz szimmetrikus (szemközti szögei kiegészítő szögek, ezért egy párhuzamos oldalon egyenlő szögek nyugszanak). Szimmetrikus trapéznál a párhuzamos oldalak felezőpontjait összekötő egyenes merőleges a párhuzamos oldalakra, így tehát a körközéppontokat összekötő egyenes merőleges a körök síkjaira.
Ezek szerint, ha a két sík egyikét párhuzamosan eltoljuk, az adódó körmetszet középpontja mindig rajt van a másik kör középpontjában síkjára emelt merőlegesen. Ez az egyenes tehát forgástengelye testünknek, testünk forgástest. A forgástengelyen átfektetett sík is körben metszi azonban a testet, és a szimmetria miatt e kör középpontja a forgástengelyen van. A szereplő forgástest tehát gömb.
II. megoldás. Tekintsük a testnek egy C középpontú k körmetszetét (5. ábra).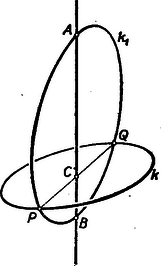
 
 
5. ábra
 

Ennek síkjára C pontban merőlegest állítunk. Fektessünk át egy síkot e merőlegesen. Ez a sík a k kört P és Q pontban, a testet pedig egy k1 körben metszi. Mivel PQ húrja ennek a körnek, e húr felezőmerőlegese, tehát az eredetileg szerkesztett merőleges k1-nek egy AB átmérőjét tartalmazza. Mivel a metsző síkot önkényesen vettük fel, kimondhatjuk, hogy az AB egyenesen átfektetett minden sík AB átmérőjű körben metszi a testet. Testünk ezért az AB átmérőjű gömbbel azonos.
 

III. megoldás. Ha testünknek egy AB húrján át két síkot fektetünk (6. ábra), két körmetszethez, az egymást A, B pontokban metsző k1 és k2 körökhöz jutunk.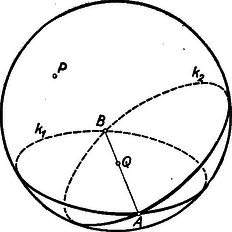
 
 
6. ábra
 

E két kör egy G gömböt határoz meg (középpontja a két körközéppontban a körsíkokra emelt merőlegesek metszéspontja, s ezeknek van metszéspontjuk, mert AB felezőmerőleges síkjában vannak, és nem párhuzamosak).
Legyen P testünk felületén egy pont. Fektessünk egy síkot a P ponton és az AB húrnak egy belső Q pontján át. Ez a sík a k1 és k2 kört négy pontban metszi, hiszen áthalad mindkét körnek belső pontján, a Q ponton. Ez a négy pont a G gömb felületén egy kört határoz meg. A felvett sík körmetszete is áthalad e négy ponton, ez a két kör tehát azonos. Ezek szerint P is G felületén van, és minden, a Q ponton áthaladó sík által G-ből kimetszett kör testünknek felületén helyezkedik el. Testünk ezért a G gömbbel azonos.
 

IV. megoldás. Legyen k1 a testnek egy körmetszete (6. ábra), legyen Q ennek a körlemeznek belső pontja, legyen P a test felületén, de nem a k1 körön, legyen végül G az a gömb, amelyik áthalad a P ponton és tartalmazza a k1 kört. A PQ egyenesen átfektetett sík a k1 kört A és B pontban metszi (hiszen tartalmazza a körnek belső Q pontját), továbbá testünket és a G gömböt is körben metszi. E két kör azonos, mert P, A és B közös pontjaik. E síkmetszetek azonosságából a test és a G gömb azonossága következik.
 

Harmadik feladat. Egy körmérkőzés során mindenki mindenkivel egyszer mérkőzött, és egyetlen mérkőzésnek sem volt döntetlen az eredménye. Bizonyítandó, hogy van olyan résztvevő, aki minden versenytársát megemlíti akkor, ha felsorolja az általa legyőzötteket, valamint azokat, akiket az általa legyőzöttek legyőztek.
 

I. megoldás. Legyen A olyan résztvevő, akinél több győzelmet senki sem aratott. Ha A nem felelne meg a feladat követelményének, akkor volna olyan B versenyző, akit sem A, sem az A által legyőzöttek nem győztek le, aki tehát mindezeket megverte, s így legalább eggyel több győzelmet aratott, mint A. Ez azonban lehetetlenség, mert A-nál több győzelmet senki sem aratott, ezért A megfelel a feladat követelményének.
 

II. megoldás. Legyen A1 a versenyzők egyike. Ha az A1 által a feladat előírása szerint végzett felsorolásban nem szerepel minden más versenyző, akkor jelöljük az általa nem említett versenyzők összességét H1-gyel. Minthogy A1 ezeket nem említette, mindegyikük megverte A1-et és az A1 által legyőzötteket. Ezért a H1 csoport minden tagja megemlíti az A1 által említetteket, ha az előírt felsorolást elvégzi. Legyen A2 egy tagja a H1 csoportnak. Ha A2 felsorolásában nem szerepel minden más versenyző, akkor tehát a nem említettek mind H1-be tartoznak, s ezek összességét H2-vel jelöljük. Mivel A2 ezeket nem említette, mindegyikük megverte A2-t és az A2 által legyőzötteket, ezért a H2 csoport minden tagja megemlíti felsorolásában az A2 által említetteket. Így tovább haladva egyre kevesebb versenyzőből álló H1, H2, ... csoportokhoz jutunk, amíg el nem érünk olyan An versenyzőhöz, akinek felsorolásában minden versenytársa szerepel. Minthogy a csökkenő csoportok sorozata nem lehet végtelen, el kell hogy jussunk ilyen versenyzőhöz.
 

Megjegyzés: A közölt megoldás burkoltan teljes indukcióra épül. Okoskodását a következőképpen is előadhatjuk: Ha csak két résztvevő van, a feladat állítása helyes; tegyük fel, hogy az állítás helyes, ha a résztvevők száma n-nél kevesebb; az n versenyző közül kiválasztott A1 versenyző egy H1 csoportot határoz meg, hacsak maga meg nem felel a követelménynek; H1-ben n-nél kevesebb résztvevő van, az indukciós feltevés szerint van tehát közöttük olyan, akinek felsorolásában H1-nek minden más tagja szerepel, a fentebbiek szerint viszont a H1-be nem tartozók mindegyikét is említi, ez a versenyző tehát megfelel a feladat követelményének.
 

III. megoldás. Az állítást teljes indukcióval bizonyítjuk. Ha csak két résztvevő van, az állítás nyilván helyes. Tegyük fel, hogy helyes az állítás, ha n résztvevő van. Ha tehát n+1 résztvevő van, akkor van az első n között olyan A résztvevő, akinek felsorolásában minden más versenyző szerepel az első n közül. Legyen B az (n+1)-edik résztvevő. Ha B is szerepel A felsorolásában, akkor A megfelel a követelménynek. Ha B nem szerepel A felsorolásában, akkor B le kellett hogy győzze A-t és azokat, akiket A legyőzött; ezért B-nek felsorolásában szerepel A és mindazok, akiket A felsorolt; ekkor tehát B megfelel a követelménynek.
 

IV. megoldás. A versenyzők egy teremben helyezkednek el. Az egyik versenyző kivezeti a teremből azokat, akiket legyőzött (esetleg senkit sem). Ha van még, aki a teremben marad, egyikük újból kivezeti azokat, akiket legyőzött a teremben maradottak közül. Ezt folytatják mindaddig, amíg valaki a termet ki nem üríti. A kiürítő legyőzte azokat, akiket kivezet, és azokat, akik korábban kivezettek, hiszen a teremben maradhatott, ez utóbbiak viszont legyőzték az általuk kivezetetteket. A kiürítő tehát minden társát megemlíti felsorolásában.
 

Megjegyzések: 1. Az első megoldás mutatja, hogy a győztes (vagy a győztesek bármelyike) megfelel a követelménynek. Nem igaz azonban, hogy csak győztes felelhet meg. Sőt még a vesztes is megfelelhet, ezt az alábbi eredménytáblázat példája bizonyítja:
ABCDE|A-1110|B0-101|C00-11|D010-1|E1000-

2. Az is lehetséges, hogy a verseny minden résztvevője megfelel a feladat követelményének. A fenti eredménytáblázat erre is példát nyújt. Mutatja, hogy 5 versenyző esetében ez is lehetséges. Felvetjük a kérdést, hogy hány résztvevős versenyben lehetséges ez.
Ha két résztvevő van, nyilvánvaló, hogy csak egyikük (a győztes) felel meg a követelménynek. Négy résztvevős versenyben sem felelhetnek meg mind a négyen a feladat követelményének. Ha ugyanis van közöttük olyan résztvevő, aki három győzelmet aratott, akkor a többinek felsorolásában ez a versenyző nem szerepel. Ha van olyan résztvevő, akit mindenki legyőzött, akkor ennek felsorolásában senki sem szerepel. Ha viszont mindannyian egy vagy két győzelmet arattak, akkor ketten egyszer-egyszer, ketten pedig kétszer-kétszer győztek, hiszen összesen hat mérkőzés volt; a két egygyőzelmes versenyző egyike legyőzte a másikat, az elsőnek felsorolásában tehát csak két versenytársa (a másik és akit az legyőzött) szerepel.
Bizonyítjuk, hogy ha a résztvevők száma nem 2 vagy 4, akkor lehetséges olyan versenyeredmény, hogy minden versenyző megfelel a feladat követelményének.
Ezt először arra az esetre bizonyítjuk, amikor a versenyzők száma, n páratlan. Állítsuk a versenyzőket egy szabályos n-szög csúcsaiba, arccal a sokszög középpontja felé. Ha mindenki azokat győzte le, akik jobboldalt állnak, akkor mindenki mindenkit felsorol. Ezt könnyű ellenőrizni.
Ha a versenyzők száma páros és 4-nél több, legyen közöttük n férfi és n nő. Ismét egy szabályos 2n-szög csúcsaiba állítjuk őket, váltakozva férfiakat és nőket. Győzze le mindenki a jobbján állókat azzal a kivétellel, hogy a nők jobboldali másodszomszédjuktól vereséget szenvednek. Ilyen versenyeredménynél mindenki felsorolja minden versenytársát függetlenül attól, hogy a sokszög átellenes csúcsaiban állók milyen eredménnyel mérkőznek. Ennek ellenőrzése sem nehéz.
A 7. ábra bemutatja az előírásunk szerinti versenyeredményeket 5 és 6 résztvevő esetében.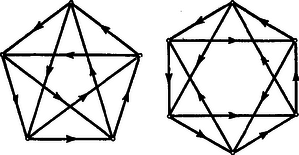
 
 
7. ábra
 

Az ábrán a nyíl a győztestől a vesztes felé irányul. A 6 versenyzős esetben az átellenesen állók mérkőzéseinek (elő sem írt) eredményét ábránk nem is jelzi.