Kezdőlap


Cím:	Képek a magyar matematika múltjából 5. -Beke Manó (1862 ápr.24-1946 jún. 27)
Szerző(k):	Obláth Richárd
Füzet:	1955/február, 33 - 42. oldal	PDF \| MathML
Témakör(ök):	Egyéb írások

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

BEKE MANÓ, akit ezekben a sorokban ifjú olvasóinknak bemutatunk, a felsőbb matematika kiváló tudósa volt, a magyar matematika történetében azonban elsősorban mint egyik legjobb tanárunk tűnik ki. Mégpedig nemcsak mint egyetemi tanár, hanem már középiskolai tanár korában országos hírű volt. Előbb a budapesti V. kerületi, Markó-utcai állami főreáliskolában (ma textilipari technikum), majd a gyakorló főgimnáziumban ‐ az úgynevezett minta gimnáziumban tanított. Mintagimnáziumnak hívták, mert a tanári pályára készülő fiatal emberek az egyetem elvégzése után többnyire ott sajátították el, kiváló mesterek vezetése mellett, a tanítás művészetét. Beke ezek között a kiváló tanárok között is a legkiválóbbak közé tartozott. Hogy szívvel-lélekkel tanár volt, az onnan is látszik, hogy 1900-ban történt egyetemi tanári kinevezése után sem mondott teljesen búcsút a középiskolának, hanem egy darabig, több országos hírnevű egyetemi tanárral együtt, tanított még a Nőképző gimnáziumban (ma Veres Pálné leánygimnázium). Mindenféle iskolafajnak szánt tankönyveket egész pályája folyamán írt, mi több, a gimnáziumi tantervek készítésében, amint egy hozzám intézett levelében írja >>tevékeny részt vett<<. Legnevezetesebb középiskolai tankönyve a >>Kőnig-Beke<<. Ez KŐNIG GYULA, a nagy magyar matematikus tankönyvének átdolgozása az újabb tanterveknek megfelelően. KÜRSCHÁK JÓZSEF írja erről az átdolgozásról, hogy igen hozzáértő, szerető, de erős kéz munkája.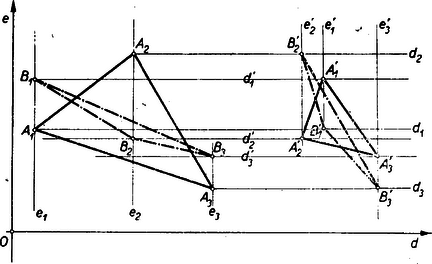
Beke Manónak a középiskolai tanításban való közreműködése mindezekkel nincs kimerítve. Századunk elején KLEIN FÉLIX, a németországi göttingeni egyetem világhírű tanára ‐ akinek hazánk kultúrájára is igen nagy befolyása volt, sőt ma is tart ‐ mozgalmat indított a középiskolai tanítás reformja érdekében. Ez a mozgalom rohamosan terjedt az egész civilizált világon, Magyarországon is. Nálunk a mozgalom lelke BEKE MANÓ és GOLDZIHER KÁROLY munkássága volt. A mozgalom fő célkitűzése, a matematika tanítás közelebb hozatala az élethez, hogy a tanuló képes legyen az iskolában tanult matematikát az életben előforduló jelenségekre alkalmazni. Ehhez szükségesnek látszott a differenciál- és integrál-számítás elemeinek és a grafikus módszernek a középiskolába való bevitele. Mindketten az iskola mindennapi életében jól használható mintákat is adtak. Beke a differenciál- és integrálszámítás elemeiről igen jó középiskolai tankönyvet írt, Goldziher pedig számos cikkben mutatta meg a grafikus módszer alkalmazását a legkülönbözőbb kérdésekre a középiskolában. Beke továbbá széles köröknek igen látogatott bevezető előadásokat tartott a differenciál- és integrálszámításba. Ezek könyv alakban is megjelentek és fényesen mutatják Beke tanári képességeit. A differenciálszámítást ma nem tanítják a középiskolában, de azoknak az olvasóinknak, akik benne tájékozódni akarnak, ma is melegen ajánlható Bekének ez a kis könyvecskéje. Beke egyetemi használatra szánt kétkötetes nagy differenciál- és integrálszámítási tankönyvet is irt, ez azonban felülmúlja olvasóink igényeit.
Nem hagyhatom szó nélkül Beke tanári sikereinek egyik titkát. Ez elbájoló kedves egyénisége. Minden tanítványával törődött. Lehetetlen volt őt nem szeretni. Tanítványainak nagy serege tényleg késő öreg koráig ragaszkodott hozzá. És ezt a kiemelkedő tanári pályát derékban törte ketté 1919-ben, a Tanácsköztársaság bukását követő fehér terror; nevetséges, mondva csinált ürüggyel megfosztották tanári állásától.
Áttérek a tudós jellemzésére. Már eddigi cikkeimben is¹ említettem, hogy a magyar matematika kezdő korának ‐ HUNYADI JENő műegyetemi tanár kiemelkedő egyéniségének hatása alatt ‐ egyik fő jellemvonása a determinánsok virtuóz kezelése volt. Ez alól a szabály alól Beke sem kivétel. A determináns elméletről igen jó tankönyvet is írt. Beke önálló eredményei egy részében, mint az akkori magyar matematikai iskola általában, főleg RADOS GUSZTÁV műegyetemi tanár eredményeit használja fel a matematika egy másik ágában, a lineáris differenciálegyenletek elméletében.
Ez az elmélet mind tudományos, mind gyakorlati, főleg műszaki szempontból igen fontos, de a felsőbb matematika magas részeihez tartozik, tehát nem beszélhetek róla. Mégsem hagyhatom szó nélkül, hogy ennek az oly fontos elméletnek a múlt század végén és századunkban sokáig PAINLEVÉ (ejtsd: Penlövé) francia miniszterelnök mellett magyar tudós, SCHLESINGER LAJOS kolozsvári egyetemi tanár volt a legnevezetesebb művelője.
Nem ismertethetem Beke egyéb felsőbb mennyiségtani kutatásait sem, azonban van érdekes elemi matematikai eredménye is, ezeket bemutatom.
Először egy elemi geometriai tételét ismertetem, amelynek bizonyításánál felhasználja a komplex számok néhány sajátságát. A tétel így szól:
Legyen adva két hasonló sokszög

\begin{matrix} A_{1} A_{2} ... A_{k} ... A_{n} és A'_{1} A'_{2} ... A'_{k} ... A'_{n} \end{matrix}

és az egymásra merőleges (de egyébként tetszőleges)

d

és

e

egyenesek. Húzzunk a két hasonló sokszög csúcsaiból párhuzamosakat a

d

és

e

egyenesekkel. Az

A_{k}

csúcson átmenő párhuzamosak legyenek

d_{k}

és

e_{k}

A'_{k}

csúcson átmenők

d'_{k}

és

e'_{k}

d_{k}

és

e'_{k}

metszéspontja

(d_{k}, e'_{k})

és

d'_{k}

e_{k}

-é (

d'_{k}

e_{k}

). Akkor a

(d_{1} e'_{1}) (d_{2} e'_{2}) ... (d_{n} e'_{n})

és

(d'_{1} e_{1}) (d'_{2} e_{2}) ... (d'_{n} e_{n})

két sokszög területe egyenlő (1. ábra).

1. ábra

A bizonyításnál elég hasonló háromszögekre szorítkozni, hiszen a sokszög háromszögekből tehető össze.
A sík

A_{k}

pontjának koordinátái valamely

O

kezdőpontú koordinátarendszerben

x_{k}

y_{k}

ehelyett mondhatom, hogy az

A_{k}

pont helyzetét a

\begin{matrix} z_{k} = x_{k} + i y_{k} \end{matrix}

komplex szám jellemzi, a

z_{k}

komplex szám képe pedig az

A_{k}

pont. A komplex szám azonban, mint olvasóink tudják, az

O A_{k}

vektornak is felfogható, amelyet hosszúsága és iránya jellemez.
A két adott hasonló háromszög tehát

A_{1} A_{2} A_{3} Δ

és

A'_{1} A'_{2} A'_{3} Δ

, vagy ha a csúcsokkal meghatározott komplex számokat adjuk meg

(z_{1} z_{2} z_{3}) Δ

és

(z'_{1} z'_{2} z'_{3}) Δ

. A feltétel szerint

\begin{matrix} (z_{1} z_{2} z_{3}) Δ \sim (z'_{1} z'_{2} z'_{3}) Δ, \end{matrix}

ami ‐ amint rögtön ki fogjuk mutatni ‐ így is kifejezhető

\begin{matrix} \frac{z_{1} - z_{2}}{z_{2} - z_{3}} = \frac{z'_{1} - z'_{2}}{z'_{2} - z'_{3}} \end{matrix}

(1)

Az egyenlőség mindkét oldalán komplex számok állnak. Két komplex szám pedig csak akkor egyenlő, ha abszolút értékeik is, argumentumaik is egyenlők.² (Az olvasó emlékezetébe idézem:

| z |

, a komplex szám abszolút értéke az őt ábrázoló vektor hosszúsága, argumentuma pedig irányának hajlásszöge a valós tengellyel.)
Az (1) egyenlőség tehát azt fejezi ki, hogy egyrészt

\begin{matrix} | \frac{z_{1} - z_{2}}{z_{2} - z_{3}} | = | \frac{z'_{1} - z'_{2}}{z'_{2} - z'_{3}} |, \end{matrix}

azaz

\begin{matrix} A_{1} A_{2} : A_{2} A_{3} = A'_{1} A'_{2} : A'_{2} : A'_{3}, \end{matrix}

másrészt pedig

\begin{matrix} arg \frac{z_{1} - z_{2}}{z_{2} - z_{3}} = arg \frac{z'_{1} - z'_{2}}{z'_{2} - z'_{3}} \end{matrix}

azaz, hogy

\begin{matrix} A_{1} A_{2} A_{3} ∢ = A'_{1} A'_{2} A'_{3} ∢, \end{matrix}

vagyis, hogy a két háromszög hasonló.
Az (1) alatti hasonlósági feltétel ebben a determináns alakban is írható³

\begin{matrix} | \begin{matrix} z_{1} & z'_{1} & 1 \\ z_{2} & z'_{2} & 1 \\ z_{3} & z'_{2} & 1 \end{matrix} | = 0, \end{matrix}

(2)

mert a determinánsnak a >>Függelék<< értelmében való kifejtése az (1) relációt adja. Írjuk be (2)-be a

z_{k}

-k és

z'_{k}

-k helyett értékeiket

z_{k} = x_{k} + i y_{k}

;

z'_{k} = x'_{k} + i y'_{k} (k = 1,2,3)

ahol

x_{k}

y_{k}

A_{k}

pont koordinátái, és a (2) egyenlet képzetes része a >>Függelékben<< adott tétel szerint

\begin{matrix} | \begin{matrix} x_{1} & y'_{1} & 1 \\ x_{2} & y'_{2} & 1 \\ x_{3} & y'_{3} & 1 \end{matrix} | - | \begin{matrix} x'_{1} & y_{1} & 1 \\ x'_{2} & y_{2} & 1 \\ x'_{3} & y_{3} & 1 \end{matrix} | = 0. \end{matrix}

(3)

x_{k}

y'_{k}

azon pont koordinátái, amelyben az

A_{k}

pontból az

y

tengellyel és az

A'_{k}

pontból az

x

tengellyel vont párhuzamosak egymást metszik, ha tehát a

d

irányt választjuk

x

tengelynek és az

e

irányt

y

tengelynek, akkor (

x'_{k}

y_{k}

) az

(e_{k}, d'_{k}) = B_{k}

pont koordinátái. Éppen így (

x_{k}

y'_{k}

) a

B'_{k} = (d, e')

pont koordinátái. A (3) egyenlet tehát azt fejezi ki, hogy ez a két háromszög

\begin{matrix} (d_{1}, e'_{1}) (d_{2}, e'_{2}) (d_{3}, e'_{3}) és (d'_{1}, e_{1}) (d'_{2}, e_{2}) (d'_{3}, e_{3}) \end{matrix}

egyenlő területű, vagyis tételünk bizonyítva van.
A tételnek sikere volt, több magyar szerző foglalkozott vele. Maga Beke megjegyzi, hogy ha a hasonló háromszögek megfelelő oldalai párhuzamosak,

d

-nek és

e

-nek nem kell merőlegeseknek lenniük. PERÉNYI KANDID ábrázoló geometriai bizonyítást ad Beke tételére. KLUG LIPÓT pedig lényegesen általánosítja és tiszta geometriai bizonyítást ad rá.
Ezekben a Lapokban egy régebbi,

^{1}

alatt idézett cikkemben felemlítettem KÜRSCHÁK JÓZSEF első dolgozatát, amelyben bebizonyította, hogy a körbe írható

n

-oldalú sokszögek közül a szabályos

n

-szög a legnagyobb területű és kerületű, a kör köré írható

n

-szögek közül pedig a szabályos

n

-szög a legkisebb területű és kerületű. Ezt a tételt Beke Manó is bebizonyította, ha nem is olyan elemien, mint Kürschák, de szintén igen elegánsan. Íme az érdekes bizonyítás.
Ha az

x = a

és

x = b

(b > a)

között az

y = f (x)

görbe az

x

tengelyhez mindenütt homorú (vagy mindenütt domború) oldalával fordul és a görbén

n

számú tetszés szerinti pontot választunk, és a

k

-ik pontban

m_{k}

tömeget helyezünk el, akkor ennek az

n

számú tömegpontnak tömegközéppontja (= súlypontja) a görbe és az

x

tengely közé esik (illetve konvex görbénél a görbe fölé). Ez magától értetődő, mert hiszen két-két pont tömegközéppontja mindig az összekötő húron van, márpedig ez a húr homorú görbénél a görbe alatt, domborúnál felette halad el. A súlypont ordinátája ezért az első esetben kisebb, a másodikban pedig nagyobb a görbe ugyanazon abszcisszájához tartozó ordinátájánál, azaz ezt a tényállást formulákkal kifejezve, az első esetben

\begin{matrix} \frac{m_{1} f (x_{1}) + m_{2} f (x_{2}) + ... + m_{n} f (x_{n})}{m_{1} + m_{2} + ... + m_{n}} < f (\frac{m_{1} x_{1} + ... + m_{n} x_{n}}{m_{1} + ... + m_{n}}) \end{matrix}

és

\begin{matrix} \frac{m_{1} f (x_{1}) + m_{2} f (x_{2}) + ... + m_{n} f (x_{n})}{m_{1} + m_{2} + ... + m_{n}} > f (\frac{m_{1} x_{1} + ... + m_{n} x_{n}}{m_{1} + ... + m_{n}}) \end{matrix}

a második esetben. Ha

m_{1} = m_{2} = ... = m_{n} = 1

, akkor homorú görbénél

\begin{matrix} f (x_{1}) + f (x_{2}) + ... f (x_{n}) < n f (\frac{x_{1} + x_{2} + ... + x_{n}}{n}), \end{matrix}

(4)

domborúnál

\begin{matrix} f (x_{1}) + f (x_{2}) + ... + f (x_{n}) > n f (\frac{x_{1} + ... + x_{n}}{n}) . \end{matrix}

(4,a)

y = sin x

görbe a

0

...

π (= 180^{\circ})

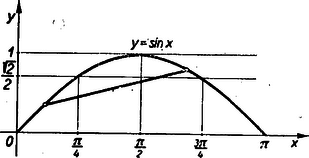
számközben mindenütt homorú oldalával fordul az

x

tengelyhez (2. ábra), tehát

π = 180^{\circ}

-nál kisebb szögekre a (4) egyenlőtlenséget alkalmazva

\begin{matrix} sin x_{1} + sin x_{2} + ... + sin x_{n} < n sin \frac{x_{1} + x_{2} + ... + x_{n}}{n} . \end{matrix}

(5)

2. ábra

Ha tehát az

O

középpontú

r

sugarú kör kerületén felvesszük az

A A_{1} A_{2}

...

A_{n - 1} A_{n}

pontokat és meghúzzuk az

A A_{1}

A_{1} A

...

A_{n - 1} A_{n}

egymást nem metsző húrokat és az

A O A_{1}

A_{1} O A_{2}

...

A_{n - 1} O A_{n}

középponti szögeket

x_{1}

x_{2}

...

x_{n}

-nel jelöljük (mindannyian kisebbek

π

-nél), akkor az

O A A_{1} A_{2}

...

A_{n} O

sokszögcikk területe (3. ábra)

\begin{matrix} t = \frac{r^{2}}{2} (sin x_{1} + sin x_{2} + ... + sin x_{n}) . \end{matrix}

Ha most az

A A_{n}

körívet

n

egyenlő részre osztjuk és az így keletkező sokszögcikket rajzoljuk meg, ennek területe

\begin{matrix} τ = \frac{n r^{2}}{2} sin \frac{x_{1} + x_{2} + ... + x_{n}}{n} . \end{matrix}

3. ábra

Az (5)-ből következik, hogy

\begin{matrix} t < τ . \end{m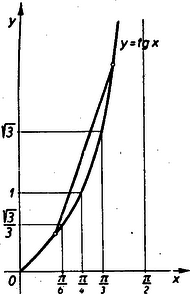atrix}

Ha tehát

x_{1} + x_{2} + ... + x_{n} = 2 π

, akkor ennek az egyenlőtlenségnek az az értelme, hogy a szabályos

n

-szög területe nagyobb bármely beírt

n

-szög területénél.
Az

A A_{1} A_{2} ... A_{n}

törtvonal hossza

\begin{matrix} s = 2 r (sin \frac{x_{1}}{2} + sin \frac{x_{2}}{2} + ... + sin \frac{x_{n}}{2}) . \end{matrix}

Ha pedig az

A A_{n}

ívet

n

egyenlő részre osztjuk fel, az így keletkező törtvonal hossza

\begin{matrix} σ = 2 r n sin \frac{x_{1} + x_{2} ... + x_{n}}{2 n} \end{matrix}

és ismét (5) szerint

\begin{matrix} s < σ, \end{matrix}

és ha megint

x_{1} + x_{2} + ... + x_{n} = 2 π

azt kapjuk, hogy a szabályos

n

-szög kerülete nagyobb bármelyik beírt

n

-szög kerületénél.

4. ábra

Teljesen hasonló módon kapja a kör körül írt sokszögről szóló megfelelő tételt. De mivel itt a sokszög oldalai érintik a kört, az oldalak hosszúságát a tangensfüggvény fejezi ki, ez pedig a

0

...

\frac{π}{2} (= 90^{\circ})

intervallumban domború oldalát fordítja az

x

tengely felé (4. ábra), tehát a (4,a) egyenlőtlenség értelmében⁴

\begin{matrix} tg x_{1} + tg x_{2} + ... + tg x_{n} > n \end{matrix}

(5,a)

amelyből ‐ teljesen ugyanúgy mint a beírt sokszög esetében ‐ következik a körülírt sokszögekre vonatkozó tétel.
Nem hallgatom el, hogy a most bemutatott bizonyításban van némi hézag, mert itt bizonyítás nélkül, csupán a jól ismert sinus- és tangens-görbékre hivatkoztam, a homorúság, illetve domborúság bizonyítása helyett. A görbék ezen sajátságai a differenciálszámítás legelemibb jól ismert tételei közé tartoznak, Beke bizonyítása tehát teljesen kifogástalan.
Beke kombinatorikus kérdésekkel is foglalkozott. Az alapfogalmakat az olvasó emlékezetébe idézem. Adott elemeknek (pl. osztályod tanulói, vagy az ábécé betűi, vagy számok stb.) bizonyos sorrendben való elrendezését, ha valamennyi elemet felhasználjuk permutációnak nevezzük, ha azonban az elemeknek csak egy részét vettük ki belőlük, pl.

n

elem közül

k

számút

(k < n)

a sorrendre való tekintet nélkül, akkor

n

elem

k

-ad osztályú kombinációit alkottuk meg. Ha a permutálandó elemek közül egyezők is vannak, akkor permutációról beszélünk azonos elemekkel. (Szokás ismétléses permutáció beszélni, azonban ez nem célszerű, mert) ismétléses kombinációról beszélünk, ha adott elemekből úgy kell bizonyos számút kiválasztani, hogy mindegyik elem többször is, akármennyiszer előfordulhat. (A permutációk esetében viszont mindegyik elem megadott számszor kell hogy előforduljon. Ezért célszerű az elnevezésben is különbséget tenni.)
Ha például csak két különböző elem

a

és

b

-nek

n

-ed osztályú permutációját akarjuk képezni úgy, hogy benne

k

számú helyet az

a

elemek és így

n - k

számú helyet a

b

elemek töltenek be ‐ tüstént látjuk, hogy az ilyen azonos elemű permutációk száma

\begin{matrix} \frac{n!}{k! (n - k)!} . \end{matrix}

(6)

Csakugyan, mivel

n

különböző elem permutációinak száma

n!

és bárhogyan cserélem is az

a

elemeket egymás között, mindig ugyanazt a permutációt kapom,

k

számú elem pedig

k!

számú módon cserélhető, az

n - k

számú

b

elem egymás között való cseréje is változatlanul hagyja a permutációt, vagyis két elemből a (6) alatti számú különböző a tagú permutáció írható fel. Gondoljuk meg most, hogy

n

elemből, hány

k

-ad osztályú kombináció készíthető? Olvasóink tudják, hogy

\begin{matrix} (\binom{n}{k}) = \frac{n (n - 1) ... (n - k + 1)}{1,2, ... k} = \frac{n!}{k! (n - k)!} \end{matrix}

tehát ugyanannyi, ahány ismétléses permutáció.
Beke ennek a két számnak megegyezését így indokolja közvetlenül: amikor a font leírt

n

elem permutációit alkotjuk, nem teszünk egyebet, mint, hogy

n

elem közül

k

elemet minden lehető módon kiválasztunk, azzal

n

elemből

k

-ad osztályú kombinációkat is alkotunk; ha ugyanis az

n

elemből egy permutációcsoportot akarunk csinálni, akkor csakis a

k

számú megegyező

a

elemet kell bizonyos módon elhelyeznünk az

n

közül

k

helyen, vagyis a megegyező elemek mindegyikének valamely sorszámot kell adnunk

1

-től

n

-ig, s a többi, üresen maradt helyet kell az egymással megegyező

n - k

számú

b

elemmel kitölteni. Így a permutációk megalkotásánál az egyetlen kombinatorikus művelet az

n

sorszám közül

k

sorszám kiválasztása, vagyis a permutációk képzése és az

n

szám (elem) közül

k

-ad osztályú kombinációk megalkotása lényegében ugyanaz a művelet.
Ugyanez a gondolat vezet a következő általánosításra is; ha az

n

elem között

k_{1}

számú elem egymás között,

k_{2}

ismét egymás között és ugyanígy

k_{3}

k_{4}

...

k_{s}

, megegyezik, ahol tehát

\begin{matrix} k_{1} + k_{2} + ... + k_{s} = n, \end{matrix}

akkor a permutációk száma

\begin{matrix} P = \frac{n!}{k_{1}! k_{2}! ... k_{s}!} = \\ = \frac{n!}{k_{1}! (n - k_{1})!} \frac{(n - k_{1})!}{k_{2}! (n - k_{1} - k_{2})!} ... \frac{[n - (k_{1} + k_{2} + ... + k_{s - 2})]!}{k_{s - 1}! k_{s}!} = \\ = (\binom{n}{k_{1}}) (\binom{n - k_{1}}{k_{2}}) ... [\binom{n - (k_{1} + ... + k_{s - 2})}{k_{s - 1}}] . \end{matrix}

Beke utóbb észrevette, hogy ez a minden számítást mellűző bizonyítási mód az ismétléses kombinációkra is kiterjeszthető, megmutatja ugyanis, hogy

n

elemnek ismétléses

k

-ad osztályú kombinációinak képzése ugyanaz a művelet, mint

n + k - 1

elem egyszerű

k

-ad osztályú kombinációinak megalkotása. A bizonyítás tovább, részletezésébe nem bocsátkozom.⁵
Most Beke algebrai dolgozatairól számolok be. Az egyik a harmadfokú egyenletről szól. Az ógörögök geometriai úton, körzővel és vonalzóval való szerkesztés útján meg tudták oldani a másodfokú egyenletet, ezt körülbelül ezer évvel ezelőtt MOHAMED BEN MUSA ALCHOVARIZMI híres arab tudós számolással végezte el. Képletét, hiszem, minden olvasóm ismeri. A harmadfokú egyenlet is korán felkeltette a matematikusok érdeklődését. A babilonok már közel 6000 évvel ezelőtt

x^{3} + x

értékeire táblázatokat készítettek, amelyek segítségével közelítőleg meg tudtak oldani harmadfokú egyenleteket. A pontos megoldás csak jóval később, időszámításunk XVI. századának elején sikerült SCIPIONE DAL FERRONE olasz tudósnak. Ez volt ezer évnél jóval hosszabb idő alatt ‐ az ógörög világ letűnése után ‐ az első nagy matematikai felfedezés. Még a XVI. század első felében 1545-ben megjelent könyvében CARDANO (ejtsd Kárdáno; az első á rövid) olasz tudós bőven foglalkozott a harmadfokú egyenlettel, melynek megoldó formuláját róla ma is Cardano-féle képletnek hívják. Már Cardanonak is feltűnt, hogy az esetben, ha az egyenlet mindhárom gyöke valós, a megoldó formulában komplex számból kell gyököt vonni. Ez a XVI. század matematikusainak jóformán leküzdhetetlen nehézséget okozott. (Ne feledjük el, hogy ekkor a betűszámtan még nem volt feltalálva.) Ezt az esetet azért >>casus irreducibilis<<-nek (= >>nem visszavezethető<< esetnek) nevezték el. Közel 350 éven át igyekeztek a legkiválóbb matematikusok ezt a zátonyt elkerülni, hogy tehát mindhárom valós gyököt valós számból vont gyökvonással megkaphassák. Hiába! Mindinkább lábra kapott az a nézet, hogy ez nem a matematikusok ügyetlenségén múlott, hanem a nehézség magában a tárgyban van, de ezt bebizonyítani igen sokáig senki sem tudta. Csak 1890-ben sikerült MOLLAME olasz tudósnak (és röviddel utána és tőle függetlenül KNESER és HÖLDER német matematikusoknak) kimutatni, hogy a casus irreducibilis esetén nem lehet a gyököket valós számból való gyökvonás segítségével megtalálni. A komplex számból való gyökvonás elkerülhetetlen, sőt ez harmadfokúnál magasabb fokú egyenletekre is áll. 1922-ben ugyanis Alfréd LÖWY (német) bebizonyította azt a szép tételt, hogy ha valamely páratlan fokú egyenletnek egynél több valós gyöke van, ezeket semmi esetre sem lehet pusztán valós számból vont gyökvonással megkapni. Beke említett dolgozatában KNESER ‐ akkor új ‐ bizonyítását ismerteti a harmadfokú egyenlet casus irreducibiliséről. (Félreértések elkerülése végett külön kiemeljük, hogy ezek a tételek nem azt állítják, hogy semmiféle valós úton nem lehet a valós gyökökhöz jutni, hanem csak azt, hogy valós számból vont gyökvonással nem lehet a gyököket megkapni. Olvasóim egy része valószínűleg ismeri a harmadfokú egyenlet >>trigonometrikus megoldását<<, amelyet még a XVI. században talált fel VIETA hírneves francia tudós, de ő nem gyökvonással, hanem a cosinus-függvény felhasználásával jut célhoz.)
A negyedfokú egyenlet megoldása csakhamar követte a harmadfokúét. Ez 1542-ben sikerült az előbb említett Cardano tanítványának, FERRARI-nak, 22 éves korában! Megoldását Lapunkban ismertettem.⁶ Azóta sok más megoldási módszert találtak a negyedfokú egyenletre. (Megjegyzem, hogy a negyedfokúnál magasabb fokú egyenleteket gyökjelek segítségével általában nem lehet megoldani. Ez a felsőbb algebra egyik nevezetes és fontos tétele.)
A negyedfokú egyenlet bármely megoldási módszerének van egy közös alapgondolata. Szükséges előzőleg egy harmadfokú egyenlet, a resolvens (=megoldó) egyenlet megoldásának ismerete, melynek gyökei szoros kapcsolatban állnak a negyedfokú egyenlet keresett gyökeivel. Minthogy a harmadfokú egyenlet megoldását a Cardano-féle formula explicite megadja, ezzel a negyedfokú egyenlet meg van oldva. Ha a megoldandó negyedfokú egyenlet keresett gyökei

x_{1}, x_{2}, x_{3}, x_{4}

akkor minden módszerben az a közös mag rejlik, hogy e gyökökből alkotható valamely racionális függvényre állítanak fel tulajdonképpen egyenletet. Ferrarinál az

x_{1} x_{2} + x_{3} x_{4}

függvényre adódik egyenlet. Könnyen látható, hogy ez a kifejezés az

1

2

3

4

indexek minden cserélésével csak három különbözőbe mehet át:

x_{1} x_{2} + x_{3} x_{4}

x_{1} x_{3} + x_{2} x_{4}

x_{1} x_{4} + x_{2} x_{3}

. Szokás egy ilyen függvényt röviden három értékűnek nevezni. DESKARTES (ejtsd Dékárt, az á rövid; 1596‐1650, a nagy filozófus, az analitikai geometria megteremtője) az

x_{1} + x_{2}

-re ad hatodfokú egyenletet, mely ha

x^{3}

együtthatója

0

, másod- és harmadfokú egyenletre vezet; Euler (1707‐1783), a tizennyolcadik század kimagasló jelentőségű nagy matematikusa

{(x_{1} + x_{2})}^{2}

-re állít fel harmadfokú egyenletet. Beke az

x_{1} x_{2}

szorzatra állít fel harmadfokú revolvens egyenletet, mégpedig a már említett Rados Gusztáv ugyanazon determináns tételei alapján, amelyeket a lineáris differenciálegyenletek elméletében is felhasznált. Így tehát ez a munkája is a magyar determináns iskolához kapcsolódik, ennek termékeny voltának igen szép bizonyítéka, épp ezért nem oly elemi, hogy részletesebben ismertethetném.
Beke nevét szép eredményei mellett elsősorban mégis szerető, lelkes nevelőmunkájával tette örökké feledhetetlenné. Ő maga írja nagyon találóan nagy analízis tankönyvének előszavában: >>Fogyatékosságai bizonnyal vannak e munkának; de azt tudom, hogy egyet minden elfogulatlan olvasó meg fog érezni benne, azt, hogy szeretettel írtam. A tárgy, a tanítás iránti szeretettel, hallgatóim és a mathematikával foglalkozó olvasóim iránti kötelességből.<< A Bolyai János Matematikai Társulat évente megjutalmazza azokat, akik kiemelkedő munkát végeznek a matematika népszerűsítése és terjesztése területén. Aligha örökíthette volna meg méltóbban a Társulat Beke Manó nevét, mint hogy ezt a díjat róla nevezte el, s az ő emlékére adja ki.

Függelék: A deteminánsokról
A szöveg okoskodását nem akartam a felhasznált segédtételek bizonyításával megszakítani. Ezért itt elmondok a determinánsokról annyit, amennyi a szövegben foglalt bizonyítás megértéséhez szükséges. Kiemeljük, hogy az ebben a >>Függelék<<-ben foglalt tárgyak, önmagukban érdekesek.
Másodrendű determinánsnak az alábbi kifejezést nevezzük és így jelöljük

\begin{matrix} | \begin{matrix} a_{1} & a_{2} \\ b_{1} & b_{2} \end{matrix} | = a_{1} b_{2} - a_{2} b_{1}, \end{matrix}

ahol

a_{1}

a_{2}

b_{1}

b_{2}

tetszőleges számok.
A harmadrendű determinánst így jelöljük

\begin{matrix} | \begin{matrix} a_{1} & a_{2} & a_{3} \\ b_{1} & b_{2} & b_{3} \\ c_{1} & c_{2} & c_{3} \end{matrix} | \end{matrix}

itt

a_{1}

a_{2}

a_{3}

b_{1}

b_{2}

b_{3}

c_{1}

c_{2}

c_{3}

a determináns elemei, az ugyanazon vízszintes sorban levő elemek, pl.

b_{1}

b_{2}

b_{3}

a determináns sorai, az ugyanazon függőleges oszlopban álló elemek, pl.

a_{1}

b_{1}

c_{1}

a determináns oszlopai. A harmadrendű determinánst úgy értelmezzük, hogy másodrendűekre vezetjük vissza

\begin{matrix} | \begin{matrix} a_{1} & a_{2} & a_{3} \\ b_{1} & b_{2} & b_{3} \\ c_{1} & c_{2} & c_{3} \end{matrix} | = a_{1} | \begin{matrix} b_{2} & b_{3} \\ c_{2} & c_{3} \end{matrix} | - a_{2} | \begin{matrix} b_{1} & b_{3} \\ c_{1} & c_{3} \end{matrix} | + a_{3} | \begin{matrix} b_{1} & b_{2} \\ c_{1} & c_{2} \end{matrix} | = \end{matrix}

\begin{matrix} = a_{1} b_{2} c_{3} - a_{1} b_{3} c_{2} - a_{2} b_{1} c_{3} + a_{2} b_{3} c_{1} + a_{3} b_{1} c_{2} - a_{3} b_{2} c_{1} . \end{matrix}

Ez >>soronként<< való kifejtés, de a tényleges kiszámítás mutatja, hogy bármely >>oszloponként<< kifejtve ugyanazt az értéket kapjuk, pl. a második oszlop szerint kifejtve

\begin{matrix} = - a_{2} | \begin{matrix} b_{1} & b_{3} \\ c_{1} & c_{3} \end{matrix} | + b_{2} | \begin{matrix} a_{1} & a_{3} \\ c_{1} & c_{3} \end{matrix} | - c_{2} | \begin{matrix} a_{1} & a_{3} \\ b_{1} & b_{3} \end{matrix} | = \end{matrix}

\begin{matrix} = - a_{2} b_{1} c_{3} + a_{2} b_{3} c_{1} + b_{2} a_{1} c_{3} - b_{2} a_{3} c_{1} - c_{2} a_{1} b_{3} + c_{2} a_{3} b_{1} . \end{matrix}

A kifejtésnél minden elemet megszorzunk azzal a determinánssal, az ún. >>aldeterminánssal<<, mely az adottból megmarad, ha kihagyjuk azt a sort és azt az oszlopot, melyekben a kiemelt elem van; az előjel pozitív, ha ezen sor és oszlop sorszámainak összege páros, negatív, ha páratlan, pl.

c_{2}

a harmadik sor második oszlopában áll

3 + 2 = 5

páratlan, tehát

c_{2}

-nek aldeterminánsával való szorzatát negatív előjellel kell venni. Látjuk, hogy a kétféle kifejtéssel ugyanahhoz az értékhez jutottunk, ez a harmadrendű determináns értéke.
A szövegben szereplő determináns tehát

\begin{matrix} | \begin{matrix} z_{1} & z'_{1} & 1 \\ z_{2} & z'_{2} & 1 \\ z_{3} & z'_{3} & 1 \end{matrix} | = z_{1} (z'_{2} - z'_{3}) - z_{2} (z'_{1} - z'_{3}) + z_{3} (z'_{1} - z'_{2}) . \end{matrix}

Írjuk be ide

z_{1}

z_{2}

z_{3}

értékét, mely a szöveg szerint

x_{1} + i y_{1}

x_{2} + i y_{2}

x_{3} + i y_{3}

| \begin{matrix} x_{1} + i y_{1} & z'_{1} & 1 \\ x_{2} + i y_{2} & z'_{2} & 1 \\ x_{3} + i y_{3} & z'_{3} & 1 \end{matrix} | = (x_{1} + i y_{1}) (z'_{2} - z'_{3}) - (x_{2} + i y_{2}) (z'_{1} - z'_{3}) - (x_{3} + i y_{3}) (z'_{1} - z'_{2}) =

= x_{1} (z'_{2} - z'_{3}) - x_{2} (z'_{1} - z'_{3}) - x_{3} (z'_{1} - z'_{3}) + i y_{1} (z'_{2} - z'_{3}) - y_{2} (z'_{1} - z'_{3}) - y_{3} (z'_{1} - z'_{3}) =

\begin{matrix} \begin{matrix}  \end{matrix} = | \begin{matrix} x_{1} & z'_{1} & 1 \\ x_{2} & z'_{2} & 1 \\ x_{3} & z'_{3} & 1 \end{matrix} | + i | \begin{matrix} y_{1} & z'_{1} & 1 \\ y_{2} & z'_{2} & 1 \\ y_{3} & z'_{3} & 1 \end{matrix} | \end{matrix}

A szöveg felhasználja továbbá az analitikus geometriának azt a tételét, hogy ha az

A_{1}

pontkoordinátái

x_{1}

y_{1}

; pontéi

x_{2}

y_{2}

; az

A_{3}

pontéi

x_{3}

y_{3}

; akkor az

A_{1} A_{2} A_{3}

háromszög kétszeres területe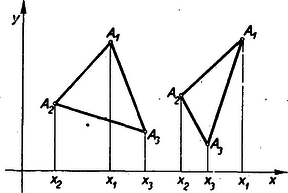

\begin{matrix} 2 T = | \begin{matrix} x_{1} & y_{1} & 1 \\ x_{2} & y_{2} & 1 \\ x_{3} & y_{3} & 1 \end{matrix} | \end{matrix}

Bizonyítsátok ezt be. Útba igazításul előrebocsátjuk, hogy a képlet adhat negatív eredményt is. Ez akkor és csak akkor következik be, ha a csúcsok megadott sorrendje a háromszög óramutató járásával megegyező irányú körüljárásának felel meg. Általában célszerű a koordináta-geometriában pozitív vagy negatív előjelet tulajdonítani sokszögek területének aszerint, hogy az óramutató járásával ellenkező, vagy egyező körüljárási iránynak megfelelő sorrendben vannak-e megbetűzve a csúcsai.

5. ábra

Könnyen beláthatjátok, hogy ilyen előjeles területekkel számolva, a háromszög bármilyen helyzete és megbetűzése mellett is (5. ábra), fennáll a

\begin{matrix} t_{A_{1} A_{2} A_{3}} = t_{A_{1} A_{2} X_{2} X_{1}} + t_{A_{2} A_{3} X_{3} X_{1}} + t_{A_{3} A_{1} X_{1} X_{3}} \end{matrix}

egyenlőség, és ebből könnyen levezethetitek a fenti területképletet. Ez mutatja az előjeles terület bevezetésének célszerűségét.

¹Obláth R.: Képek a magyar matematika múltjából, III. Kürschák József: Középiskolai Matematikai Lapok VIII. kötet, 1954., 97‐104. oldal, ugyanez IV. Arany Dániel: uitt. IX. kötet, 1954, 65‐71. oldal.

²Az érdeklődő bővebb felvilágosítás nyerhet egy kitűnő szakköri füzetből: Rieger R.: A komplex számok.

³Lásd a >>Függelék<<-et a cikk végén.

⁴Ebben a bizonyításban [az (5) formula bizonyításánál] felhasználtuk azt a tételt, hogy az $r$ sugarú kör $2 α$ nyílású központi szögével befogott húrja $2 r sin α$ , felhasználjuk majd azt is, hogy a szög száraival befogott, a szögfelezőre merőleges érintő pedig $2 r$