Cím: Egy geometriai rokonságról
Szerző(k):  Gönyei Antal 
Füzet: 1955/január, 1 - 7. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek
Hivatkozás(ok):Feladatok: 1955/február: 665. matematika feladat, SCMF0675 feladat dekódolása nem sikerült.
1955/március: SCMF0675

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Néhány egyszerű összefüggést mutatok be, amelyek segítségével bizonyos elemi geometriai tételeket egyszerűen bizonyíthatunk.
Vegyünk szemügyre a síkháromszögre vonatkozó néhány egyszerű tételt: a háromszög magasságai egy pontban metszik egymást; az oldalak felezési pontjában állított merőlegesek metszőpontja a háromszög köré írható kör középpontja; a háromszög köré írható kör kerületének bármely pontjáról a háromszög oldalaira bocsátott merőlegesek talppontjai egy egyenesre esnek (Simson egyenes); a háromszög magassági pontja, súlypontja és a körülírható kör középpontja egy egyenesen fekszik (Euler-egyenes). Mindezekben a tételekben a merőleges egyenesek nagy szerepet játszanak. Ezért helyesnek látszik általánosságban felvetni a kérdést, hogy milyen viszonyok keletkeznek akkor. ha a sík egy pontjából két egymást metsző egyenesre merőlegest bocsátunk és e merőlegesek talppontjait összekötjük? Az itt mutatkozó összefüggéseket alkalmazhatjuk a többi között a háromszög tulajdonságainak felderítésénél is. Részben a pont és a hozzárendelt egyenes közti ezen rokonságban fellépő összefüggésekkel, részben paralelogrammák néhány egyszerű tulajdonságával fogunk az alábbiakban foglalkozni és alkalmazásukkal főleg a háromszög tulajdonságaira.
2. A síkban felveszünk két egymást a szöggel metsző egyenest. Nevezzük ezeket tengelyeknek és ezt az egyszerű rendszer ∑(α) rendszernek. Legyen O a tengelyek metszéspontja és S egy ettől különböző pont. Bocsássunk S-ből mindkét tengelyre merőlegest és kössük össze e merőlegeseknek a tengelyekkel való metszéspontjait, az így nyert s egyenest az S ponthoz adjungáltnak fogjuk nevezni a ∑(α) rendszerben (1. ábra).

 
 

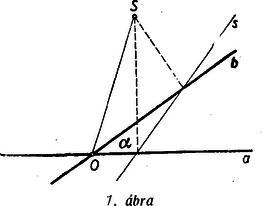
Fordítva bármely a tengelyektől különböző egyeneshez egyértelműen megszerkeszthető az a pont, amelyhez az egyenes van adjungálva. Az egyik tengelyre a metszéspontjukban állított merőleges bármely pontjához a másik tengely tartozik, s így a tengelyekhez nem rendelhetünk egyértelműen egy pontot. Viszont minden az O ponton átmenő egyeneshez az O pontot kapjuk meg.
Legyen a tengelyek metszéspontja O, akkor vizsgálni fogjuk az S ponthoz vezető OS sugarat is.
3. Az így nyert rendszerben először szögösszefüggéseket fogunk vizsgálni, célszerű lesz azonban a szokásostól kissé eltérő módon számítanunk a szögeket, mégpedig a következő módon:
Két egyenes szögén az alábbiakban azt a szöget fogjuk érteni, amivel az elsőt az óramutató járásával ellentétes irányba elforgatva valamely pontja körül először kerül a másodikkal párhuzamos helyzetbe (2. ábra).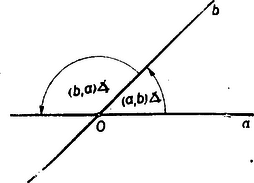
 
 
2. ábra
 

Az így meghatározott szög mindig 0 és 180∘ közti érték. Az ≫először≪ szót el is hagyhatjuk a meghatározásból, ha megegyezünk abban, hogy két szöget, mely csak 180∘ egy egész többszörösében különbözik, nem tekintünk különbözőnek. A továbbiakban ezzel a megállapodással fogjuk számítani a szögeket, és két nem lényegesen különböző szög közé egyenlőségjelet fogunk írni, akkor is ha (pl. fokokban mért) mérőszámaik ugyan nem egyeznek meg, de csak 180∘ egy egész többszörösében különböznek, s így egyenlő szögek alatt hajló egyenespárok szögeit mérik; ilyen értelemben tehát 180∘=0∘. Az így számított szög definíció szerint függ az egyenesek sorrendjétől is. Nyilvánvaló, az előbbi megjegyzés értelmében használva az egyenlőségjelet, hogy
(a,b)∢+(b,a)∢=0(=180∘),vagyis(b,a)∢=-(a,b)∢
(Negatív szögön érthetjük az óramutató járásával egyező irányban mért szöget, vagy érthetünk olyan 0 és 180∘ közti szöget is, amelyik az adott negatív szögből 180∘ egy alkalmas többszörösének hozzáadásával keletkezik.) Azt, hogy (a,b)∢=α fogjuk úgy is mondani, hogy a b egyenes a-hoz α szög alatt hajlik. Megjegyezzük, hogy a kerületi szögek tétele a szög ilyen számítása mellett egyöntetűen úgy fogalmazható, hogy ha A és B a kör két adott pontja, P pedig tetszésszerinti pontja a körnek, akkor az APB∢ (vagyis a (PA,PB)∢) független a P pont helyzetétől ‐ még attól is, hogy az A és B közti melyik íven van 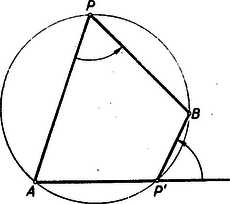P.
 
 
3. ábra
 

Ha ugyanis P és P' a két különböző íven van (3. ábra), akkor az APB∢ és AP'B∢ egyikét az APBP' húrnégyszög egyik belső szöge méri, a másikat a szemközti szög külső szöge; ezek pedig a húrnégyszögek tétele szerint egyenlők, s így
APB∢=AP'B∢

4. Térjünk most vissza az előző pont elején felvetett kérdésre. Legyen adva az a és b tengelyek alkotta ∑(α) rendszer (α=(a,b)∢,) legyen a tengelyek metszéspontja O. Legyen S tetszés szerinti pont, vetületei az a, illetőleg b tengelyen legyenek A és B, a rajtuk átmenő egyenes pedig s. Legyen (a,OS)∢=ζ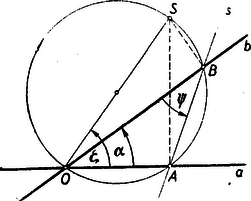,(b,s)=ψ (4. ábra).
 
 
4. ábra
 

Mivel merőlegeseket bocsátottunk a tengelyekre, O,S,A és B egy körön vannak, O és S e kör átellenes pontjai. A ζ szög az AS^ íven nyugszik, ψ szög pedig az OA^ íven. Mivel a két ív együtt az OS félkört adja, (mindig az óramutató járásával ellentétes irányban bejárható ívet számítva) így a ζ+ψ összeg a félkörön nyugvó kerületi szöggel, azaz 90∘-kal egyenlő (természetesen megállapodásainknak megfelelően 180∘ egy egész többszörösétől esetleg eltekintve). Az olvasó ellenőrizze, hogy okoskodásunk hegyes és tompaszögű, valamint (a,b)∢-nél kisebb és nagyobb ζ szögekre egyaránt helyes*. (A kör teljes körüljárását természetesen figyelmen kívül hagyhatjuk, mert annak 180∘-os kerületi szög felel meg.)
Bebizonyítottuk tehát, hogy
ζ+ψ=(a,OS)∢+(b,AB)∢=90∘

5. A fenti tétel alkalmazhatóságát a háromszögekre vonatkozó néhány tétel bizonyításán mutatjuk be.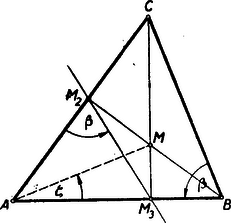
 
 
5. ábra
 

a) Tekintsük az ABC háromszög (5. ábra) AB és AC oldalát egy ∑(α) rendszernek. Akkor a CM3 és BM2 magasságok M metszéspontjához adjungált egyenes a talppontokat összekötő M2M3 egyenes. Bizonyítsuk be, hogy a háromszög magasságai egy pontban metszik egymást. Azt fogjuk belátni, hogy AM⊥BC, vagyis AM a harmadik magasság egyenese. Az előző pont eredményeinek felhasználásához a ψ=(AC,M2M3)∢=AM2M3∢ értékét kell megállapítanunk. Mivel C,M2,M3 és B pontok egy körön fekszenek CM2M3∢=CBM3∢=β, s így az említett összefüggés szerint
BAM∢=ζ=90∘-ψ=90∘-β,
de ez éppen azt fejezi ki, hogy AM⊥BC, és ezt akartuk igazolni. (Az olvasó ellenőrizze, hogy a bizonyítás ‐ éppen a szögekre tett megállapodások következtében ‐ hegyes és tompaszögű háromszögre egyaránt érvényes.)
b) Hasonlóképp könnyen következik a nyert szögösszefüggésekből, hogy a felezési pontokban emelt merőlegesek egy pontban metszik egymást. Ugyanis ‐ a BC,CA,AB oldalak felezőpontját rendre F1,F2,F3-mal jelölve ‐ az F2F3 egyenes az AB és AC oldalak felező merőlegesének O metszéspontjában adjungált egyenes az AB,AC egyenesek ∑(α) rendszerére nézve (6, ábra).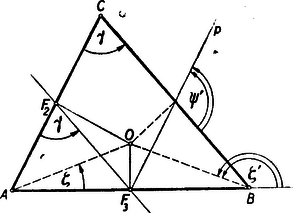
 
 
6. ábra
 

Mivel F2F3||BC, így ψ=(AC,F2F3)∢=AF2F3∢=γ, így ζ=F3AO∢=90∘-γ. Az O pont az AB oldal felező merőlegesén van, tehát AOB▵ egyenlőszárú. Vizsgáljuk most a BA,BC alkotta ∑(180∘-β) rendszerre vonatkozóan az O ponthoz adjungált p egyenest. Ez mindenesetre átmegy F3-on. Ezenkívül meghatározhatjuk a BC egyenessel bezárt szögét. Az AOB egyenlőszárú háromszögből
ζ'=(BA,BO)∢=180∘-BAO∢=180∘-F3AO∢=90∘+γ,
s így
ψ'=(BC,p)=90∘-ζ'=-γ,
vagyis
(p,BC)∢=γ.
Ez azonban azt jelenti, hogy p||AC, tehát p középvonala a háromszögnek, s így BC-t F1 felezőpontjában metszi. Ez a pont azonban O merőleges vetülete is a BC egyenesen, tehát a harmadik oldal felező merőlegesen is átmegy O-n.
c) Bocsássunk most egy tetszés szerinti P pontból merőlegest egy háromszög oldalaira. A BC,CA,AB oldalakra bocsátott merőlegesek talppontjai legyenek rendre P1,P2,P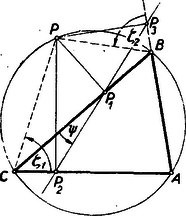3 (7. ábra).
 
 
7. ábra
 

Mikor esik a három pont egy egyenesbe, azaz mikor teljesül pl. a (BC,P1P2)∢=(BC,P1P3)∢ egyenlőség? A kérdés úgy is fogalmazható, hogy mikor esik egybe a P-hez a CA,CB egyenesekből álló ∑(180∘-β) rendszerben adjungált egyenes a BA,BC alkotta ∑(180∘-β) rendszerben P-hez adjungált egyenessel. Ennek azonban szükséges és elégséges feltétele, hogy
ζ1=(CA,CP)∢=ζ2=(BA,BP)∢;
ez az egyenlet pedig éppen azt jelenti, hogy P,A,B,C egy körön vannak. A P pontnak az oldalakon való merőleges vetületei tehát akkor és csakis akkor esnek egy egyenesbe, ha P az ABC▵ köré írt körön van. Ezzel a Simson-egyenesekre vonatkozó tételt nyertük mindjárt annak megfordításával együtt. Meggondolásunk azt is mutatja, hogy ha a P pont a körön elmozdul, akkor a hozzátartozó Simson-egyenes akkora szöggel fordul el, de ellentétes irányban, mint amekkora szögben a P pont elmozdulása látszik a kerület valamely pontjából (pl. valamelyik háromszögcsúcsból.) Átellenes pontokhoz tartozó Simson-egyenesek pl. merőlegesek egymásra.
6. Tekintsünk most egy egyenesre illeszkedő S1,S2,S3,... pontsort. Legyenek a pontok vetületei egy ∑(α) rendszer a, ill. b tengelyén A1,A2,A3,..., ill. B1,B2,B3,.... Ekkor S1S2:S1S3=A1A2:A1A3=B1B2:B1B3, és ez fennáll a pontsorok bármely három-három megfelelő pontjára, hacsak az Ai, vagy Bi pontok nem esnek egybe. Ilyenkor azt mondjuk, hogy az egymásnak megfeleltetett pontok hasonló pontsort alkotnak. A föntieket ekkor úgy fejezhetjük ki, hogy egy egyenesen sorakozó pontokhoz adjungált egyenesek a rendszer két tengelyén az eredeti S1,S2,S3... pontsorhoz hasonló pontsorokat metszenek ki, s így természetesen egymáshoz is hasonló a két tengelyen kimetszett pontsor.
A tételt meg is fordíthatjuk:
Ha a két tengelyen hasonló pontsorokat jelölünk ki, akkor a megfelelő pontokat összekötő egyenesekhez adjungált; pontok egy egyenesen sorakoznak.
Nyilvánvaló az állítás abban az esetben, ha a tengelyen kijelölt hasonló pontsoroknak egy-egy megfelelő pontja összeesik a tengelyek O metszéspontjában. Ebben az esetben a megfelelő pontokat összekötő egyenesek párhuzamosak. Így pl. az S1A1B1▵-ből egy O középpontú nyújtással származtathatók az S2A2B2▵, S3A3B3▵... háromszögek, s így S1,S2,S3,... csúcsaik is egy O-n átmenő egyenesen sorakoznak.
Legyen most kijelölve a tengelyeken tetszőlegesen két hasonló pontsor. Az a tengelyen kijelölt két pontnak, A1-nek és A2-nek a megfelelője legyen B1 és B2 (8. 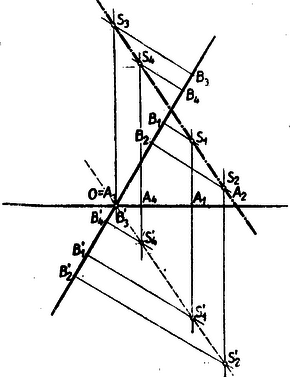ábra).
 
 
8. ábra
 

Keressük meg a b tengely azon B3 pontját, amely az a tengely A3=O pontjának felel meg (tehát melyre B1B2:B1B3=A1A2:A1O és amely aszerint van a B1B2 szakaszon, vagy azon kívül, amint O belül vagy kívül van az A1A2 szakaszon). Toljuk ezután el a B-pontsort a b tengely mentén úgy, hogy B3 egybeessék az O ponttal. Ha az így keletkezett B'1,B'2... pontsor pontjait kötjük össze az A-pontsor megfelelő pontjaival, akkor a keletkező párhuzamos egyenesekhez adjungált pontokról már láttuk, hogy egy O-n átmenő egyenesen sorakoznak. Húzzuk meg az A-pontsor, ill. B' pontsor pontjain át a megfelelő tengelyre merőleges egyeneseket, ezek paralelogrammákat alkotnak. Ha most a B'-pontsort a merőleges egyenesekkel együtt visszatoljuk az eredeti helyére, akkor a keletkezett paralelogrammarendszer nem változtatja alakját, csak párhuzamosan eltolódik az a tengelyre merőleges egyenesek között és így az S'1,S'2,... pontok is egy, az előbbivel párhuzamos egyenesen fekvő S1S2,... pontokba mennek át; ez volt a bizonyítandó állítás.
Megjegyezzük, hogy az eddigiekben nem volt lényeges szerepe annak, hogy merőlegeseket bocsátottunk a tengelyekre. A talált összefüggések változatlanul érvényben maradnak, ha az a és b tengelyen kívül két irányt, i1-et és i2-t adunk meg (i1∦a,i2∦b) és egy S pontból i1 irányú egyenessel metsszük az a tengelyt, 2 irányúval b-t, és a metszéspontok összekötését rendeljük az S ponthoz. Alkalmazásképpen megmutatjuk, hogy a háromszög köré írt kör O középpontja, M magasságpontja és S súlypontja egy egyenesen van. Az előbbi két pont létezését 5a) és b)-ben bizonyítottuk, a súlypont létezését fogadjuk egyelőre el és azt a tulajdonságát is, hogy a súlyvonalat a csúcstól számítva 2:1 arányban osztja. Világos, hogy az M,S,O pontoknak az AB oldalon való M3,S3,F3 vetületei (9. ábra) megegyeznek a C,S és F3 pontok vetületeivel.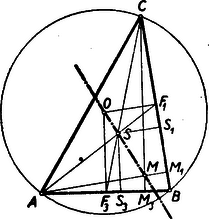
 
 
9. ábra
 

Az utóbbiak egy egyenesen fekszenek és az AB oldalon 2:1 arányt létesítenek, mert CS=2SF3. Hasonló érvényes azonban pl. a BC oldalon levő M1,S1,F1 vetületekre is, amelyek az A,S és F1 vetületének tekinthetők. A megfelelő pontokat összekötő egyenesek tehát e két oldalon egyenlő arányokat metszenek ki és így ezen egyenesek olyan pontokhoz vannak adjungálva, melyek egy egyenesre esnek. Mivel ezek a pontok az M,S és O pontok, tehát ezek egy egyenesre esnek és távolságuk aránya MS:SO=2:1, mint a vetületeiké.
7. Ha az előző pontban szerepelt párhuzamos oldalból paralelogrammákból összetett rendszert közelebbről megvizsgáljuk, ezek átlóira olyan önmagában is érdekes tételt fogunk találni, amelynek speciális esete lesz a súlyvonalak metszéséről szóló tétel, amit az előzőkben ismertnek tettünk fel.
Legyen adva egy ABCD paralelogramma. Valamely P pontból húzzunk az oldalakkal párhuzamos EF és GH egyeneseket. (A betűzést a 10. ábra mutatja.)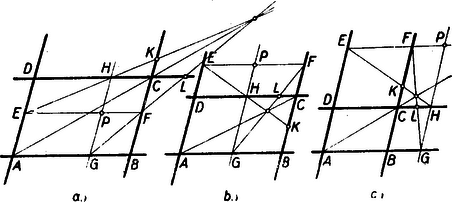
 
 
10. ábra
 

Négy olyan paralelogramma keletkezik, amelyek egyik csúcsa P, és az ezzel szemközti csúcsai az eredeti paralelogrammában átellenes csúcsok. Húzzuk meg az eredeti paralelogramma másik két csúcsát összekötő átlót és a kiválasztott két paralelogramma P-n át nem menő átlóját. (10. ábra.) Bebizonyítjuk, hogy ez a három átló. egy ponton halad keresztül. Legyen EH és BC metszéspontja K, továbbá FG és CD metszéspontja L, ekkor elegendő megmutatni, hogy
CKAE=CLAG,
mert ebből következik, hogy EH és FG olyan pontokban metszik AC-t, amelyektől a C-ig és A-ig terjedő szakaszok aránya egyenlő. tehát e két metszéspont egybeesik*.
A kívánt egyenlőséget megkaphatjuk, ha CK-t az egymáshoz hasonló KCH▵ és HPE▵ háromszögek segítségével HC-vel hasonlítjuk össze, CL-t pedig a HC-vel egyenlő PF szakasszal, azt használva, hogy LCF▵∼FPG▵. Az előbbi hasonlóság folytán
KCCH=HPPE=CFAG
az utóbbiból pedig
CLCF=FPPG=CHAE,
amiből
CLCH=CFAE.
Osszuk el az utolsó egyenlőséggel az elsőt, nyerjük, hogy
KCCL=AEAG,
ami csak átrendezett alakja. Ezzel állításunkat igazoljuk. Ellenőrizzük, hogy a bizonyítás a P pont minden lehetséges helyzetére érvényes (a), b), c) ábra).
Válasszuk P pont gyanánt az adott paralelogramma AC átlóján azt a P pontot, melyre nézve CP=AC, ekkor a 11. ábra mutatja, hogy tételünk az EGP▵-re vonatkozóan a súlyvonalak találkozására vonatkozó tételbe megy át (10c ábra speciális esete), és az ábráról leolvasható az osztásarányra vonatkozó állítás is.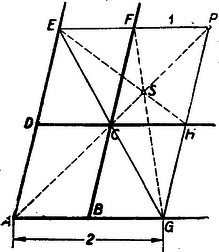
 
 
11. ábra
 

Megjegyezzük még a következőt: Három-három párhuzamos egyenest húzva a keletkezett ábrában, hat különböző módon választható ki a három-három egy ponton átmenő átló. A keletkező hat metszéspontról megmutatható, hogy ezek közül három-három egy egyenesen van, amint azt a 12. ábra mutatja.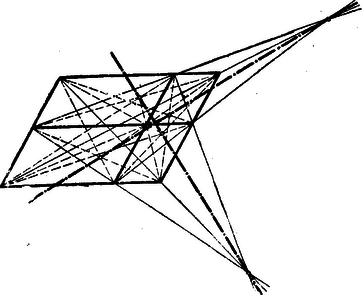
 
 
12. ábra
 

Az elmondottak gyakorlására jövő számtól kezdve fog néhány feladat megjelenni.
*Ez az összefüggés is általánosítható: ha csak annyit kötünk ki, hogy
(a,AS)∢=(b,BS)∢=λ legyen, akkor hasonló gondolatmenettel (a,OS)∢+(b,AB)∢=λ adódik.

*Az ábrából leolvasható az is, hogy vagy mindkét átló A és C közt, vagy mindkettő az AC szakaszon kívül metszi az AC átlót, s így valóban egybe kell esnie a két metszéspontnak.