Cím: Az 1954. évi Arany Dániel matematikai tanulóverseny (3., befejező közlemény)
Füzet: 1954/november, 82 - 96. oldal  PDF  |  MathML 
Témakör(ök): Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az alábbiakban közöljük a haladók (II. osztályosok) versenyén kitűzött feladatok megoldását.

 

Az I. forduló feladatai
 

I. feladat: Szerkesszünk derékszögű háromszöget, ha adott az átfogó c és tudjuk azt, hogy az átfogóhoz tartozó súlyvonal mértani középarányos a két befogó között.
 

I. megoldás: Nem megy az általánosság rovására, ha egyszer és mindenkorra feltételezzük, hogy a>b. Pythagoras tétele szerint
a2+b2=c2,(1)
feltételünk szerint (mivel a súlyvonal c2)
2ab=c22(2)
(1) és (2)-t összeadva, ill. kivonva nyerjük
(a+b)2=3c22,(a-b)2=c22,
amiből
a+b=c32=c62,(3)a-b=c22(4)

A szerkesztés ezek alapján többféleképpen is történhetik.
α) (3) és (4) összeadásából nyerjük, hogy a=c6+c24, amely szakasz könnyen szerkeszthető (c6 mértani középarányos 2c és 3c között, c2 pedig c és 2c között). a és c birtokában a keresett háromszög szerkesztése triviális.
β) (3) alapján a+b, mint mértani középarányos c és 32c között megszerkeszthető. Az a+b és c szakaszok birtokában a háromszög szerkesztése a tankönyvből ismeretes (1. ábra).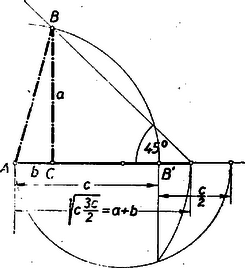
 
 
1. ábra
 

γ) (4) szerint a-b olyan négyzet átlója, melynek oldala c2. a-b és c birtokában a derékszögű háromszög ismert módon (2. ábra) megszerkeszthető.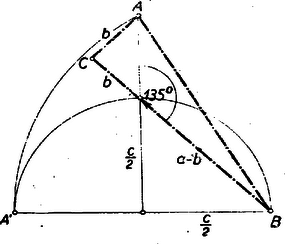
 
 
2. ábra
 

Mindhárom esetben könnyen kimutatható, hogy az így megszerkesztett háromszög tényleg eleget tesz követelményünknek. Pl. az utóbbi esetben Pythagoras-tétele alapján
(a-b)2=a2+b2-2ab=2⋅c24=c22,
amiből
2ab=a2+b2-c22=c2-c22=c22,
és így tényleg
ab=c24.
Oldalak helyett szögeket is kiszámíthatunk, mint azt az alábbi II‐V. megoldások mutatják.
 

II. megoldás: Képzeljük a feladatot megoldottnak. A betűzést a 3. ábra mutatja.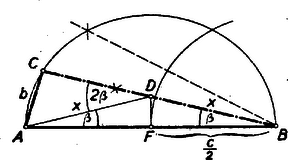
 
 
3. ábra
 

Jelöljük az AB átfogó felező pontját F-fel, tehát FA=FB=c2. Az F-ben az átfogóra emelt merőleges messe a BC=a befogót D-ben. Legyen AD=DB=x.
A szögek egyenlősége miatt
ABC▵∼DBF▵,
és így
x:c2=c:a,
amiből
x=c22a.
De a feltétel szerint
c2=4ab,
és így
x=2b

Az ACD derékszögű háromszögben sinCDA∢=sin2β=bx=b2b=12, amiből
2β=30∘,vagyisβ=15∘,
mely szög könnyen szerkeszthető.
 

III. megoldás: A jelöléseket megtartva
a=csinα,b=ccosα.
A feltétel szerint
ab=c2sinαcosα=c24,
vagyis, 2c2-tel szorozva
2sinαcosα=12,
azaz
sin2α=12,
ahonnan (0<2α<180)
2α=30∘ill.150∘,
a>b miatt
α=75∘.

IV. megoldás: Az előbbi jelöléseket megtartva jelöljük az AFC∢-et φ-vel (4. 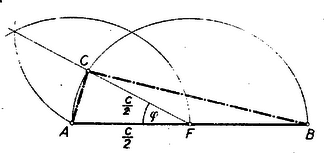ábra).
 
 
4. ábra
 

Az AFC▵ területe a fele az ABC▵ területének. Tehát
12⋅c2⋅c2sinφ=ab4,
vagyis c2sinφ=2ab, amiből sinφ=2abc2.
De a feltétel szerint ab=c24, vagyis 2ab=c22, és így sinφ=12, vagyis φ=30∘. A C pont megszerkesztése a körülírt körön egyszerűbb már nem lehet.
 

V. megoldás: A legegyszerűbb megoldáshoz (ha nem is a legegyszerűbb szerkesztéshez) jutunk, ha feltételünket >>helyesen<< olvassuk.
Feltételünk szerint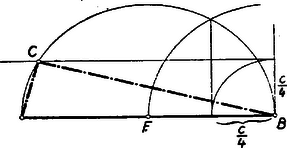
ab=c24=c⋅c4.
ab a háromszög kétszeres területe, tehát c⋅c4 is az, vagyis c4 a háromszögnek az átfogóhoz tartozó magassága. A szerkesztést az 5. ábra mutatja.
 
 
5. ábra
 

Az utóbbi megoldásnál közvetlenül nyilvánvaló, hogy a megszerkesztett háromszög teljesíti a feladatban kirótt feltételt: ab=c⋅c4=c24. A II‐IV. megoldásnál (ahol tulajdonképpen kiszámítottuk, hogy α=75∘ és β=15∘) a következőképpen igazolhatjuk szerkesztésünk helyességét:
a=ccos15∘,b=csin15∘,
és így
ab=c2sin15∘cos15∘=c2sin30∘2=c24.

De anélkül, hogy a háromszög oldalait vagy szögeit kiszámítanánk, is megoldhatjuk feladatunkat, amint azt az alábbi VI‐VII. megoldások mutatják.
 

VI. megoldás: Képzeljük a feladatot megoldottnak. A betűzést a 6. ábra mutatja.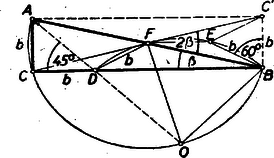
 
 
6. ábra
 

Szerkesszük meg azt a kört, amely a CF egyenest F-ben érinti és a B csúcsponton is átmegy. Legyen ennek a körnek középpontja O és messe ez a kör a BC befogót másodszor D-ben. Mivel CF2=CB⋅CD, vagyis (c2)2=a⋅CD, azért a feladat szerint CD=b. Ha kimutatjuk, hogy O rajta van az AB fölé, mint átmérő fölé rajzolt körön és BO=c2, továbbá, hogy a D pont rajta van az AO egyenesen, akkor lényegében a II. megoldásban nyert szerkesztéshez jutottunk, de más indokolással.
Mivel BFC egyenlőszárú háromszögből
FCD'∢=FBD∢=β,
másrészt CFD∢=β, mint az FD^ ív fölötti húr-érintőszög, azért CDF egyenlő szárú háromszög és
FD=CD=b.
Az FB^ ívhez tartozó húr-érintő szög, mint a BFC▵ külső szög 2β, tehát ez az ív kétszerese az FD^ ívnek. Az E felezőpontját berajzolva, a húrokra FE=EB=b és FE∥DB.
Az ABC▵-et téglalappá egészítve ki FE ennek a középvonalán fekszik. Így C'E=EB=b, másrészt BC'=AC=b, tehát a BEC' szabályos háromszögből C'BE∢=60∘, s így
EBD∢=2β=30∘,

Ugyanekkorák az FB^ íven nyugvó kerületi szögek, és így a középponti szög
BOF∢=60∘ésBO=FO=BF=c2
a kör sugara. A BOD egyenlőszárú háromszög alapján nyugvó szög
DBO∢=60∘-β=60∘-15∘=45∘=BDO∢.

Ebből következik, hogy ez a háromszög derékszögű, továbbá A, D és O egy egyenesbe esnek és O (a C-vel együtt) az AB fölötti félkörön van.
Eszerint a szerkesztés menete: az AB=c átmérő fölötti félkört a BO=c2 távolsággal elmetszve, majd az AO egyenest az OD=c2 távolsággal elmetszve, a BD egyenes metszi ki az AB fölötti félkörből a keresett háromszög C csúcsát.
A szerkesztés igazolása: Mivel az ABO▵ szögei 30∘, 60∘ és 90∘, azért az O körüli c2 sugarú körnek az AB-vel való F metszéspontjára FOB▵ szabályos, mert FBO∢=60∘, tehát F felezőpont, CF=c2, mint a derékszögű háromszög súlyvonala, továbbá BFO∢=60∘. BOD egyenlőszárú derékszögű háromszög, tehát ADC∢=DAC∢=45∘, CD=CA=b; másrészt az AFC egyenlőszárú háromszögben CAF∢=45∘+30∘=75∘, s így az AFC∢=30∘. Ebből következik, hogy
CFO∢=180∘-30∘-60∘=90∘.
Így CF érinti az O középpontú kört, s így
CF2=CD⋅CB=ba,
tehát az ABC▵ megfelel a kívánalmaknak.
 

VII. megoldás: Az adott AB=c átfogó fölé rajzolt F középpontú Thales-körben az AB átmérőre merőleges sugár végpontját jelöljük O-val (7. ábr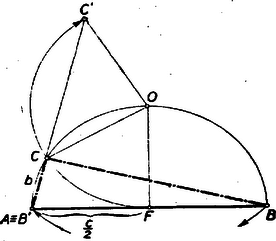a).
 
 
7. ábra
 

O körül OF=c2 sugárral rajzolt kör metszi ki a Thales-körből a keresett C pontot. (Ez tulajdonképpen az V. megoldásban nyert szerkesztés, ismét más megindokolással.)
Forgassuk el a BC=a befogót O körül 90∘-kal az óra járásával megegyező irányban, akkor a B elforgatása a B' az A pontba kerül, C elforgatása pedig C', és B'C'≡AC'⊥BC. Mivel AC is merőleges BC-re, azért a C' pont az AC befogó meghosszabbításán fekszik.
A szerkesztés szerint az AF=c2 az O körül rajzolt körnek az A pontból húzott érintője, és így
AC'⋅AC=ab=(c2)2.

2. feladat: Oldjuk meg a következő egyenletrendszert:
(x+y)(x2+y2)=a,(x-y)(x2-y2)=b.



I. megoldás: A baloldalakat polinommá alakítva
x3+x2y+xy2+y3=a,(1)x3-x2y-xy2+y3=b(2)
egyenletekhez jutunk. Miután mind a két egyenlet harmadfokú és az egyik sem látszik alacsonyabb fokúra redukálhatónak, az egyenletrendszer megoldásánál majd köbgyökvonást kell végeznünk. Arra törekszünk tehát, hogy a változók lehető egyszerű kifejezésének teljes köbét állítsuk elő.
Összeadva (1)-et és (2)-t, továbbá osztva kettővel
x3+y3=a+b2.(3)
A baloldalt 3x2y+3xy2 egészítené ki (x+y) köbére. Vegyük észre, ha kivonjuk (2)-t, éppen ilyen alakú kifejezéshez jutunk:
2x2y+2xy2=a-b.
Mindkét oldalt 32-vel szorozva nyerjük
3x2y+3xy2=3(a-b)2(4)

(3) és (4) összege
x3+3x2y+3xy2+y3=(x+y)3=a+b+3a-3b2=2a-b.
Köbgyököt vonva
x+y=2a-b13.(5)
Másrészt (4)-et így alakíthatjuk át:
xy(x+y)=a-b2,
melybe x+y (5) alatt nyert értékét behelyettesítve,
xy=a-b22a-b13.(6)
Eszerint x és y a következő másodfokú egyenlet gyökei
z2-2a-b13⋅z+a-b22a-b13=0.
Megoldva az egyenletet:
z1=x1=y2=2a-b13+(2a-b)213-2(a-b)2a-b132,z2=x2=y1=2a-b13-(2a-b)213-2(a-b)2a-b132.



II. megoldás: Vezessünk be új változókat. Legyen
x+y=u,ésxy=v.
Az új változók behelyettesítése céljából átalakítjuk egyenleteinket
(x+y)(x2+y2)=(x+y)[(x+y)2-2xy]=a(x-y)(x2-y2)=(x-y)2(x+y)=[(x+y)2-4xy](x+y)=b.


Elvégezve a behelyettesítést
u(u2-2v)=u3-2uv=a,(1)(u2-4v)u=u3-4uv=b.(2)


Vonjuk ki (1) kétszereséből (2)-őt
u3=2a-b;u=2a-b13=x+y(3)
(1)-ből kifejezzük v-t u-val, majd behelyettesítjük u-nak (3)-ból nyert értékét
v=u3-a2u=a-b22a-b13=xy.(4)
Minthogy (3) és (4) megegyezik az I. megoldás (5) és (6) egyenletével az I. megoldás szerint számolhatunk tovább.
 

Megjegyzés: Mindkét adott függvény az x és y szimmetrikus kifejezése, amin azt értjük, hogy x és y felcserélésével változatlan marad. Az u=x+y és v=xy kifejezéseket a két változó elemi szimmetrikus kifejezéseinek nevezzük. Bebizonyítható, hogy bármely szimmetrikus kifejezés pusztán a négy alapművelet segítségével kifejezhető az elemi szimmetrikus kifejezésekkel, mégpedig egyértelműen. A II. megoldásban ezt tettük.
 

3. feladat. Két szám összege 173717. A két szám 4-jegyű különbségének törzstényezői között nincsen egyjegyű szám. Az egyik szám osztható 1558-cal. Melyik ez a két szám ?
 

I. megoldás: Az egyik szám nyilván annyival kisebb az összeg felénél, amennyivel a másik az összeg felénél nagyobb. Mivel a két szám különbsége kisebb, mint 10000, ezért a keresett számok, ha 1731772=86858,5 helyébe m-et írunk, m-5000 és m+5000, vagyis 81859 és 91859 között vannak.
Keressük az első 1558-cal osztható számot a természetes számok sorában 81858 után. Mivel
52<818581558<53
azért 1558⋅53=82574=m-4284,5 az első szám, a szóban forgó számközben, mely osztható 1558-cal. Az m-4284,5 számnak párja m+4284,5 s így a különbség 2⋅4284,5=8569. A következő két megfelelő számpár különbsége nyilván 8569-2⋅1558=5453, végül az utolsó számpár különbsége 5453-3116=2337.
2337-nek és 5453-nak van egyjegyű osztója (3 illetőleg 7), azonban 8569(=11⋅19⋅41)-nek nincs egyjegyű osztója, és így az egyetlen megoldás 82574 és 82574+8569=91143.
 

II. megoldás: Az összeg és az egyik szám minden közös osztója osztja a másik számot is, és így osztója a két szám különbségének.
Tehát (173717, 1558)=779=19⋅411 a két szám különbségének is osztója.
Tehát a különbség 19⋅41⋅k alakú, ahol k nem tartalmazhat egyjegyű törzstényezőt.
Mivel a feladat szerint 1000≤19⋅41⋅k≤9999, azért
1000779≤k≤9999772=12,...,
vagyis
2≤k≤12.

Tehát feltételeinknek csak a k=11 érték felel meg, és így a különbség
779⋅11=8569.
Ha a keresett két számot x és y-nal jelöljük, akkor
x+y=173717,x-y=178569,
amiből
x=91143(=3⋅13⋅19⋅41)y=82574(=2⋅19⋅41⋅53).

A II. forduló feladatai
 

1. feladat: Két futó α és β versenyt futnak egy körpályán. A táv egy kör, rajt és cél a P pontban. Mikor α eléri a táv felét jelentő Q pontot, β 16 m-rel van mögötte. Egy későbbi időpontban a két futó helyzete tükrös a PQ átmérőre nézve. 1215 másodperccel ezen időpont után β eléri Q pontot és további 131315 másodperc múlva α célba ér. Mekkora a futók sebessége és mekkora a táv ? (Feltételezzük, hogy mind a két futó egyenletes sebességgel fut.)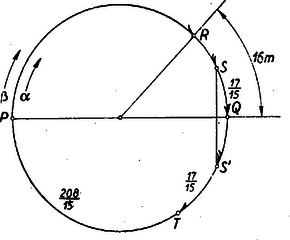
 
 
1. ábra
 

I. megoldás: Az 1. ábrán a kör belső oldalán α helyzetét, a külsőn ugyanakkor β helyzetét tüntettük fel egyforma fél nyilakkal és köztük a megfelelő futóknak egy-egy ív befutására szükséges idejét.
Válasszuk a befutási időket ismeretlennek: fussa be α a félkört x másodperc alatt, β pedig y másodperc alatt. Mivel egyenletesen futnak, α bármely utat xy-szor annyi idő alatt fut be, mint amennyi alatt β ezt az utat befutja. Az SQ^ utat β befutotta 1715 sec alatt, α tehát 1715xy sec alatt futja be ezt az utat és a vele egyenlő QS'^ utat is; ugyanannyi idő alatt β viszont R-ből S-be érkezett.
Nézzük meg, mennyi idő alatt tette meg α a QP második félkört és mennyi alatt β a PQ^ első félkört. Tudjuk, hogy ezen idő éppen x-szel, ill. y-nal egyenlő. A QS'^, S'T^, TP^ ívek befutására α-nak szükséges időket összeadva
x=1715xy+1715+20815=17x15y+15.(1)
Míg β elért P-ből R-be, addig α a félkört futotta be, tehát ezalatt x sec telt el. Az RS^ úthoz pedig, amint láttuk, 1715xy sec kellett, tehát
y=x+17x15y+1715.(2)
(1)-et (2)-ből levonva
y-x=x-20815,azaz15y=30x-208.
15y ezen értékét (1)-be helyettesítve
x=17x30x-208+15,30x2-675x+3120=0.
15-tel egyszerűsítve
2x2-45x+208=0,ahonnanx1=16,[x2=6,5].

A második gyök negatív y értéket adna, így feladatunk megoldása x=16 sec, y=27215=18215 sec.
Ezek szerint a 16 m-es RQ^ út befutására β-nak
1715xy+1715=1715(16⋅15272+1)=1715⋅3217=3215sec-ra
volt szüksége, tehát sebessége
vβ=16⋅1532=152=7,5m/sec;
α sebessége
vα=vβyx=152⋅27215⋅16=152⋅1715=172=8,5m/sec.

A pálya s fél hossza annyiszorosa a 16 méternek, mint y a 3215-nek, tehát az egész pálya hossza
2s=2⋅16⋅27215⋅1532=272m.

II. megoldás: Válasszuk a pálya s félhosszát és az SQ^=QS'^=d távolságot (méterben mérve) ismeretlennek. Míg α a PS'^=s+d utat teszi meg, β befutja a PS^=s-d utat, tehát (tekintettel arra, hogy egyenletesen fut a két futó) ugyanazon idő alatt α mindig s+ds-d-szer akkora utat tesz meg, mint β. Így míg β az RS^ utat teszi meg, α útjára (amely QS'=d)
RS^s+ds-d=d,tehátRS^=ds-ds+d
adódik. Így
RS^+SQ^=ds-ds+d+d=16.(1)

Másrészt míg β az SQ^=d utat futja be, α útja
S'T=ds+ds-d,
és nyilván
TP^=20817S'T^=208d(s+d)17(s-d).
Így
QP^=s=d+d(s+d)s-d+208d(s+d)17(s-d)=d+225d(s+d)17(s-d).

Ebből az egyenletből meghatározhatjuk az sd=z arányt. d-vel osztva és a törtet d-vel egyszerűsítve
z=1+225(z+1)17(z-1),17(z-1)2=225(z+1)=225(z-1)+450.

Innen z-1=u-ra
17u2-225u-450=0.

Csak a pozitív gyök felel meg a feladatnak, tehát
u=15,sd=u+1=16,s=16d,
s ezen értékét (1)-be helyettesítve
d1517+d=3217d=16,d=17⋅1632=172m.
Így
s=16⋅172=136m,
a teljes pálya hossza pedig
2s=272m.
1715 sec alatt α az
S'T=d(s+d)s-d=1715d=1715⋅172
utat teszi meg, β pedig d utat. Így sebességük
vα=172=8,5m/sec,vβ=172:1715=7,5m/sec.

Megjegyzés: Az egyenletrendszert többféle alakban is felírhatjuk, aszerint, hogy milyen mennyiségeket választunk ismeretlennek. Az itt adott megoldások megmutatják, hogy egy a tényeket jól szemléltető vázlat megkímél fölösleges ismeretlenek bevezetésétől és megóv attól a veszélytől, hogy a köztük felállított egyenletek esetleg nem függetlenek egymástól. A versenyzők kivétel nélkül 3‐4 ismeretlennel dolgoztak. Kétségtelen, hogy az egyes egyenletek felállítása így egyrészt könnyebb, de másrészt könnyen előfordulhat ‐ és több versenyzővel meg is esett ‐ hogy a feladat valamelyik állítását kétféleképpen írjuk fel egyenlet alakjában, míg egy másik állítást figyelmen kívül hagyunk. Ez esetben is megegyezik az ismeretlenek száma az egyenletek számával, de az utóbbiak nem függetlenek egymástól, és így a végén határozatlan egyenlethez jutunk, végtelen sok megoldással. Ilyen esetben az első gondolatunk az legyen, hogy talán nem minden feltételt használtunk fel.
A másodfokú egyenletrendszer megoldása bizonyos ügyességet kíván, mert a helyettesítésekkel könnyen magasabbfokú egyenletre juthatunk. Ez nem következik be abban az esetben, ha az egyik ismeretlent első fokú egyenletből fejezzük ki és a nyert elsőfokú kifejezést helyettesítjük be a másodfokú egyenletbe. Gyakorlati okokból jó, ha első pillanatra lényegtelennek látszó körülményeket sem hagyunk figyelmen kívül. Példánkban vα-ra, vβ-ra és d-re eleve kisebb számértéket várunk, mint s-re. Ezért, ha módunkban van, az ismeretlenek közül legelőször s-et küszöböljük ki, mert ha végül vα-ra, vβ-ra vagy d-re nyerünk egy másodfokú egyenletet, ez bizonyára egyszerűbb alakú lesz, mintha s kiszámítására nyerünk egyenletet és így sok numerikus számítást takaríthatunk meg. Sok versenyző saját kárán jöhetett rá, hogy érdemes átgondolni ilyen mellékesnek látszó körülményeket is.
 

III. megoldás: A mozgási feladatokat előnyösen oldhatjuk meg grafikus úton. A vízszintes tengelyre az időt, a függőlegesre a megtett utat mérjük rá. Az út és idő összetartozó értékeit pontokkal ábrázoljuk; e pontok összessége a mozgás grafikonja. Az egyenletes mozgás grafikonja egyenes vonal. Az idő-tengellyel bezárt szögének tangense a mozgó test sebességét adja meg.
Példánkban az út-tengelyre a pályát kiegyenesítve rakjuk rá, kezdőpontja és a végpontja egyaránt P (utóbbit a 2. ábrán P*-gal jelöltük), a táv felezési pontja Q. A távot és a mozgások sebességét nem ismerjük, ezért csak vázlatszerű grafikont tudunk készíteni, amelyről az ismeretlenek számértékét nem fogjuk tudni közvetlenül leolvasni, de könnyű lesz azokat kiszámítani a vázlatszerű grafikonról is leolvasható egyszerű összefüggésekből.
α mozgását a P pontból kiinduló ugyancsak α-val jelölt egyenessel ábrázoljuk; β sebessége kisebb, ezért a mozgását az α-nál kevésbé meredek β egyenes ábrázolja (2. ábra).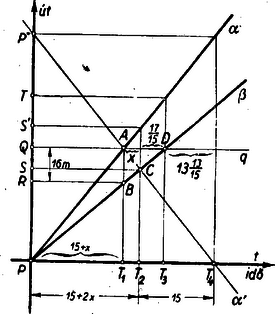
 
 
2. ábra
 

T1 időpontban, mikorra α megtette a táv felét. β hátrább van 16 m-rel, melyet függőlegesen bejelöltünk: AB=16 m. A tükrös helyzet időpontja T2, amikor β helyzetét a C pont jellemzi. A C pontot α tükörképe az α' egyenes metszi ki a β egyenesből.
β a táv felét T3 időpontban éri el. Ennek a helyzetnek a grafikonon a D pont felel meg, amelyben a β egyenes metszi a Q-n átmenő, t idő-tengellyel párhuzamos q egyenest.
α célbaérésének időpontját T4-gyel jelöltük. Ez a pont az időtengelyen a P kezdőponttól kétszer akkora távolságra van, mint T1 és az α' egyenes keresztül megy T4-en.
Az időkülönbségeket a q középvonalon tüntettük fel: T2-T1-et x-szel jelöltük, a feladatból ismert T3-T2=1715, T4-T3=131315, T4-T2=15, T1-0=T4-T1=15+x.
A t és a vele párhuzamos q egyenes metszi a C ponton átmenő egyeneseket. Tekintsük a metszéspontokat megfelelő pontoknak és a megfelelő pontok által határolt egyenes szakaszokat megfelelő szakaszoknak. (Tehát A-nak megfelel T4 pont, D-nek megfelel P; az AD szakasznak megfelel a T4P szakasz.) A megfelelő szakaszok aránya egyenlő, tehát
x:15=1715:(15+2x),átalakítva2x2+15x-17=0.

Ennek az egyenletnek egyik gyöke x=1, a másik negatív, tehát a feladat szerint értelmetlen.
Ezután x segítségével az ismeretleneket az ábrából tüstént kifejezhetjük és kiszámíthatjuk.
β sebességét vβ-t (a β egyenes emelkedési szögének tangensét) az ADB derékszögű háromszögből határozhatjuk meg:
vβ=16x+1715=161+1715=24032=7,5m/sec.

A PDT3 derékszögű háromszögből a táv fele:
s=DT3=PT3⋅vβ=(15+2x+1715)⋅7,5=136m.

Végül a PAT1 derékszögű háromszögből, α sebessége:
vα=AT1PT1=s15+x=13616=8,5m/sec.

Feladatunkat ezzel megoldottuk és a hosszúság-egység és idő-egység megválasztása után a két mozgást grafikusan, léptékhelyesen is ábrázolhatjuk.
 

2. feladat: Adva van egy kör, továbbá 3 egyenes a, b, i melyek közül a és b metszi a kört. Szerkesszünk i-vel párhuzamos oly egyeneseket, amelyek a másik két egyenest és a kört úgy metszik, hogy az egyik kör metszésponttól az egyik egyenesig terjedő szakasz egyenlő a másik körmetszésponttól a másik egyenesig terjedő szakasszal.
 

Megoldás: A kör minden pontjából húzzunk az i egyenessel párhuzamos egyenest, messe ez b-t a B pontban, a kört pedig másodszor az L pontban. L-ből mérjük rá a KL egyenesre mindkét irányban a KB távolságot. A keletkező mértani helynek az a egyenessel való metszéspontjaiban i-vel párhuzamosan húzott egyenesek adják a feladat megoldásait.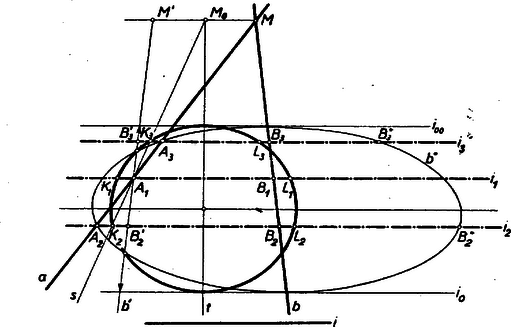
 
 
3. ábra
 

Jelöljük az i-vel párhuzamos körérintőket i0- és i00-val, a b-nek a i irányra merőleges t körátmérőre vonatkozó tükörképét b'-vel.
Ha KB-vel ellentétes irányú LB' távolságokat mérünk fel (lásd az ábrán az i2 és i3 egyeneseken a B'2 ill. B'3 pontokat), akkor, ha a K végigfut a körön a B' pontok kétszer futják be a b'-n ennek i0 és i00 közti szakaszát. (Az ábrán a két végpontot nyíllal jelöltük.) Ennek a szakasznak az a egyenessel való A1 metszéspontján át ‐ ha van ilyen ‐ az i-vel párhuzamosan húzott i1 egyenes szolgáltatja a feladat egyik megoldását. (Nevezhetjük >>tükrös megoldás<<-nak, mert K1A1=L1B egymásnak tükörképei t-re nézve.)
A mértani hely másik részét megkapjuk, ha az i-vel párhuzamos egyenesekre a KB szakaszokkal egyirányú LB* távolságokat mérünk. Ha K befutja a teljes kört (tehát a K és L pontok felcserélődnek) a B* pontok zárt görbét futnak be, mely görbéből minden i0 és i00 közti párhuzamoson 2‐2 pont fekszik. Ennek a görbének az a egyenessel lehetséges metszéspontjait (A2A3) kellene megszerkeszteni. Erre azonban a talált mértani hely már nem alkalmas. Hasznát vehetjük azonban itt is a b' egyenesnek.
Tegyük fel, hogy az A2-n átmenő i2 megoldás már meg van szerkesztve; ennek metszéspontja a körrel K2 és L2, a b és b' egyenesekkel és B2 és B'2, végül K2A2=L2B2 és e távolságok egyirányúak. Mivel b' szerkesztése szerint L2B2=K2B2', azért K2A2=K2B'2 és e távolságok már ellentétes irányúak, azaz K2 az A2B'2 szakasz felezőpontja. Így a K2 és hasonlóképpen a K3 is, rajta van azon a vonalon, melyet az i0 és i00 közti i-vel párhuzamos egyenesek a és b' közé eső szakaszainak felezőpontjai alkotnak. Tudjuk azonban, hogy ilyen szakaszt bárhol megrajzolva, a keletkező háromszögnek s súlyvonalán vannak az összes felezőpontok, tehát a súlyvonalnak az i0 és i00 közé eső szakaszán lesz az újabb mértani hely, melynek közös pontjai a körrel adják a K2-t és K3-at. (Ha a és b metszéspontja M a rajz keretén belül van, akkor az MM' szakasz felezőpontja M0 nyilván a t tengelyen van és az A1M0 egyenes az A1MM'▵ keresett s súlyvonala.) A K2 és K3 pontokon át i-vel húzott párhuzamosak i2 és i3 megoldások, amelyeken K2A2=L2B2 ill. K3A3=L3B3 egyirányúak. Ilyen fajta (nem tükrös) megoldások száma 2, 1 (2 egybeeső), ill. 0 aszerint, amint s két különböző pontban metszi a kört, érinti a kört, vagy nem metszi a kört.
Az összes megoldások száma tehát 3, 2, 1 vagy 0.
 

Megjegyzés: A b* görbe úgy keletkezett az adott körből, hogy azt a b' egyenestől mindkét oldalon egy adott i irányban kétszeresre nyújtottuk. Ha speciálisan az egyenes átmérő és az irány erre merőleges (a nyújtás vagy zsugorítás pedig tetszés szerinti arányú), akkor a III. osztály tananyagában szerepel annak bizonyítása, hogy a körből így keletkező görbe ellipszis. A IV. reálosztályosok az ábrázoló-geometriai órákról azt is tudják, hogy tetszőleges egyenes, tetszőleges irányú és tetszőleges arányú nyújtás (vagy zsugorítás) esetén is, a kör ellipszisbe megy át, és a kör- és ellipszis-rendszer közötti geometriai rokonságot >>affinitás<<-nak hívjuk. A IV. reálosztályosok még azt is tudják, hogy pl. a tengelyeivel megadott ellipszisnek egy egyenessel való metszéspontjait úgy szerkeszthetjük meg, hogy az ellipszist affin vonatkozásba hozzuk egy körrel, az ellipszis-rendszerben megadott egyenesnek megszerkesztjük az affin megfelelőjét a körrendszerben, ez utóbbinak a körrel való metszéspontjait visszavisszük az ellipszis-rendszerbe. Jelen esetben tulajdonképpen az ellipszis-rendszerben megadott a≡s* egyenesnek megszerkesztettük a körrendszerbe a megfelelőjét s-et, 1:2 arányú zsugorítással.
Figyeljük végül meg, hogy az i1 megoldáson egyszerre fennáll K1A1=L1B1 és K1B1=L1A1. Ez is és az a tény is, hogy míg K befutja a kört, B' kétszer halad végig a b' szóbajövő szakaszán (a mértani helynek ez a része egyenes szakasszá fajuló ellipszisnek tekinthető), vagyis az A1 pont, mint e mértani helynek és az a egyenesnek metszéspontja, kétszeresen számít, azt mutatja, hogy tulajdonképpen az i1 megoldás is kétszeresen számít.
 

3. feladat: Az
x2+2xy+5y2-6xz-22yz+16z
kifejezést alakítsuk át egy háromtagú, egy kéttagú és egy egytagú kifejezés teljes négyzetének algebrai összegére.
 

Megoldás: A keresett kéttagú kifejezésben az egyik változó nem fordulhat elő. Határozzuk meg a háromtagú kifejezést úgy, hogy négyzetét levonva az adott kifejezésből, a különbség már csak két változót tartalmazzon, pl. ne tartalmazza x-et. Ezt úgy érhetjük el, hogy az adott kifejezést x szerint rendezzük.
F(x,y,z)=x2+2x(y-3z)+(5y2-22yz+16z2).(1)

Ezután az első két, x-et tartalmazó, tagot teljes négyzetté egészítjük ki
x2+2(y-3z)=[x+(y-3z)]2-(y-3z)2.

Ezt (1)-be helyettesítve és összevonva
F(x,y,z)=(x+y-3z)2-4y2-16yz+7z2.(2)

Most az y-os tagokat egészítsük ki teljes négyzetté.
4y2-16yz=(2y-4z)2-16z2.

Ezt (2)-be helyettesítve
F(x,y,z)=(x+y-3z)2+(2y-4z)2-16z2==(x+y-3z)2+(2y-4z)2-(3z)2.



Megjegyzés: A bemutatott eljárással bármely háromváltozós polinom, melynek minden tagja csak egy változó négyzetét vagy csak két változó szorzatát tartalmazza, átalakítható egy háromtagú, egy kéttagú és egy egytagú polinom teljes négyzetének algebrai összegévé. Az átalakítás azonban általában irracionális együtthatókat hozhat be, még ha az eredeti kifejezés együtthatói racionális vagy éppen egész számok voltak is. Természetesen előfordulhat, hogy az egyes kifejezésekben egyes tagok hiányoznak (együtthatójuk 0), esetleg a 3 négyzetes kifejezés közül valamelyik teljesen hiányozhat.
Végül megemlítjük azt is, hogy a négyzetösszeggé alakítás másképpen is lehetséges. pl. a fenti kifejezésre igazolható az
F(x,y,z)=(34x+114y-4z)2-(17441x+414y)2+(641x)2
átalakítás helyessége is és sok másé.
1Ilyenkor a zárójel jelenti a zárójelbe foglalt, vesszővel elválasztott számok legnagyobb közös osztóját.