Kezdőlap


Cím:	Az 1954. évi Arany Dániel matematikai tanulóverseny (2. közlemény)
Füzet:	1954/október, 33 - 39. oldal	PDF \| MathML
Témakör(ök):	Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Alábbiakban közöljük a kezdők (I. osztály) versenyén kitűzött feladatok megoldásait.

Az I. forduló feladatai

1. feladat. Egy háromszög két csúcsát a kör kerületén rögzítjük, a harmadik csúcs végigfut a körön. Mi a háromszögbe írható körök középpontjának mértani helye?

I. megoldás: Legyen

A

és

B

a két rögzített pont,

F_{1}

és

F_{2}

A B

húrra merőleges átmérőnek végpontjai és

C

a harmadik csúcs, mely egyelőre mozogjon az

A F_{2} B

köríven (1. ábra).

1. ábra

A kerületi szögek tétele alapján az

A C B ∢ = γ

szög állandó. A beírt kör

O

középpontja a szögfelezők metszéspontja, így az

\begin{matrix} A O B ▵ - ből az A O B ∢ = 180^{\circ} - \frac{α + β}{2} = 180^{\circ} - \frac{180^{\circ} - γ}{2} = 90^{\circ} + \frac{γ}{2}, \end{matrix}

vagyis az

O

pontból az

A B

húr az állandó

90^{\circ} + \frac{γ}{2}

szög alatt látszik. Tehát az

O

pontok mértani helyének egy része az

A B

húrhoz tartozó,

90 + \frac{γ}{2}

szögnek megfelelő látókörív. E látókörív középpontja az

A B

húrra merőleges

F_{1} F_{2}

egyenesnek az a pontja, amelyben az ugyanazon íven nyugvó középponti szög

2 (90 + \frac{γ}{2}) = 180^{\circ} + γ

, vagyis amelyből az

A B

húr

360^{\circ} - (180^{\circ} + γ) = 180^{\circ} - γ

szög alatt látszik; ez a pont pedig az

F_{1}

pont, mert az

A C B F_{1}

húrnégyszögben az

A F_{1} B ∢ = 180^{\circ} - γ

, mint a

γ

szöggel szembenfekvő szög.
Ugyanúgy kimutatható, hogy ha a

C

pont a

B F_{1} A

íven mozog, akkor az

O

pont leírja az

F_{2}

középpontú

B A

ívet. Tehát a feltételeket kielégítő

O

pontok szükségképpen az

F_{1}

és

F_{2}

középpontú, a kör belsejében fekvő,

A B

köríveken fekszenek. Meg kell még mutatnunk, hogy ‐ fordítva ‐ e köríveknek minden pontja eleget tesz a követelményeknek. Az

A O B ∢ = 90^{\circ} + \frac{γ}{2}

szög

A O

, ill.

B O

szárára tükrözzük az

A B

egyenest (1. ábra). A tükörképek az

A B

egyenessel, annak az

F_{2}

-t tartalmazó oldalán

2 \cdot O A B ∢

és

2 \cdot O B A ∢

nagyságú szögeket zárnak be. E két szög összege

\begin{matrix} 2 (O A B ∢ + O B A ∢) = 2 [180^{\circ} - (90^{\circ} + \frac{γ}{2})] = 180^{\circ} - γ \end{matrix}

tompaszög, tehát ezek az egyenesek metszik egymást az

A B

határolta,

F_{2}

-t tartalmazó félsíkban és

γ

nagyságú szöget zárnak be. Ezek szerint

C

metszéspontjuk rajta van az

A F_{2} B

köríven és

O

, mint két szögfelező metszéspontja, az

A B C ▵

beírt körének középpontja, tehát megvan a mértani helyet definiáló tulajdonsága.
Most már kimondhatjuk, hogy a keresett mértani hely: az

F_{1}

és

F_{2}

középpontú, a kör belsejében fekvő,

\hat{A B}

körívek.

II. megoldás: Ha

C_{1} \equiv F_{2}

, akkor az

A C_{1} B ▵

-be írt kör középpontja legyen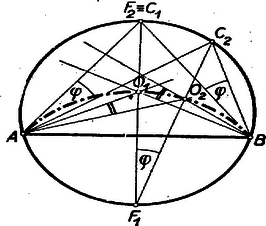

O_{1}

(2. ábra).

2. ábra

A F_{2} B

körív egy tetszőleges

C_{2}

pontjához tartozó

A B C_{2} ▵

beírt körének középpontja, vagyis szögfelezőinek metszéspontja legyen

O_{2}

. A változó

C

csúcspontból kiinduló szögfelező, a kerületi szögek tétele alapján, mindenkor átmegy az

F_{1}

ponton

\begin{matrix} C_{1} A C_{2} ∢ = C_{1} F_{1} C_{2} ∢ = C_{1} B C_{2} ∢ = φ, \end{matrix}

mint ugyanazon a köríven

(\hat{C_{1} C_{2}})

nyugvó kerületi szögek.
Ebből következik, hogy ha a háromszög

f_{c}

szögfelezője

F_{1}

körül

φ

szöggel elfordul, akkor
1. az

a

és

b

oldal is

φ

szöggel fordul el és következésképpen
2. a másik két szögfelező

\frac{φ}{2}

szöggel (az ábrán kétszeres ívvel jelölve) fordul el.
Tehát

\begin{matrix} O_{1} A O_{2} ∢ = O_{1} B O_{2} ∢ = \frac{φ}{2} . \end{matrix}

Mivel a kerületi szögek tétele megfordítható, ez azt jelenti, hogy az

O_{1}

és

O_{2}

pontok rajta vannak azon az

\hat{A B}

köríven, melynek az

O_{1} O_{2}

ívhez tartozó középponti szöge

2 \cdot \frac{φ}{2} = φ

, és maga a középpont pedig rajta van az

A B

húrt merőlegesen felező

F_{1} F_{2}

egyenesen. Mivel ‐ mint láttuk ‐ éppen

O_{1} F_{1} O_{2} ∢ = φ

, azért az

O

pontokat tartalmazó

\hat{A B}

körív középpontja

F_{1}

. A fenti bizonyítás megfordításával kimutatható, hogy a szóbanforgó körív minden pontja eleget tesz feltételeinknek.
Ugyanígy végezhető a bizonyítás az

A F_{1} B

körívre nézve.

III. megoldás:

F_{1} A B ∢ = F_{1} C B ∢ = \frac{γ}{2}

, mint kerületi szögek (3. ábra).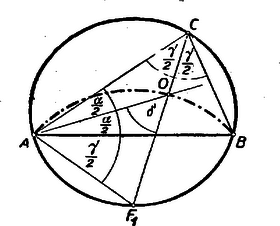

3. ábra

A O C ▵

O

-nál fekvő külső szöge

δ

egyenlő a két belső szög összegével, vagyis

δ = \frac{α}{2} + \frac{γ}{2}

, amiből következik, hogy az

A O F_{1} ▵

egyenlő szárú, tehát

\begin{matrix} F_{1} O = F_{1} A . \end{matrix}

Ugyanígy végezhető a szükségesség e bizonyítása az

\hat{A F_{1} B}

köríven fekvő

C

pontokhoz tartozó

O

pontokra nézve is. E bizonyítások megfordításból következik, hogy a szükséges feltétel elégséges is, és ezzel bebizonyítottuk, hogy az

O

pontok mértani helye az

F_{1}

, és

F_{2}

középpontú,

A

(és

B

) ponton átmenő köröknek, az adott kör belsejébe eső ívei.

2. feladat. Bizonyítsuk be, hogyha négy egymásután következő természetes szám szorzatához

1

-et adunk, négyzetszámot kapunk.

I. megoldás: Legyenek a számok:

a

a + 1

a + 2

a + 3

, ahol

a \geq 1

. Feladatunk tehát az

\begin{matrix} a (a + 1) (a + 2) (a + 3) + 1 \end{matrix}

kifejezést polinommá alakítani és arról kimutatni, hogy ez egy másik polinom négyzete.

\begin{matrix} (a^{2} + a) (a^{2} + 5 a + 6) + 1 = a^{4} + 6 a^{3} + 11 a^{2} + 6 a + 1. \end{matrix}

Ez a polinom csak olyan háromtagú polinom négyzeteként keletkezhetett, amelynek első tagja

a^{2}

és harmadik tagja

1

. A középső tagját,

x

-et, meg kell határozni.

\begin{matrix} {(a^{2} + x + 1)}^{2} = a^{4} + 2 a^{2} x + x^{2} + 2 a^{2} + 2 x + 1. \end{matrix}

A nyert kifejezést összehasonlítva polinomunkkal nyerjük, hogy

x = 3 a

esetén a két polinom tagról-tagra megegyezik, tehát

\begin{matrix} a (a + 1) (a + 2) (a + 3) + 1 = {(a^{2} + 3 a + 1)}^{2} . \end{matrix}

II. megoldás: Ügyesebb a szorzatot úgy csoportosítani, hogy az első és utolsó, továbbá a két középső tényezőt szorozzuk össze:

\begin{matrix} a (a + 1) (a + 2) (a + 3) + 1 = (a^{2} + 3 a) (a^{2} + 3 a + 2) + 1 = \\ = {(a^{2} + 3 a)}^{2} + 2 (a^{2} + 3 a) + 1 = {(a^{2} + 3 a + 1)}^{2} . \end{matrix}

3. feladat. Adva van egy háromszög két oldalának összege és a két oldal bezárta szög. Szerkesszük meg a háromszöget úgy, hogy a harmadik oldal a lehető legkisebb legyen.

I. megoldás: Legyen adva a

d = a + b

távolság és a

γ

szög. Képzeljük a feladatot megoldottnak (1. ábra).

1. ábra

Ha az

a = B C

oldalt

C

-n túl

b

-vel meghosszabbítjuk:

C D = b

és így

B D = a + b = d

.
Az

A D C

egyenlőszárú háromszögnek a

C

csúcsnál fekvő külső szöge

γ

, és így az

A D B ∢ = \frac{γ}{2}

.
A szerkesztés kiindulása tehát: Az adott

d = B D

távolság

D

végpontjában felmérjük az adott

γ

szög felét. Az így nyert száron lesz rajta az

A

pont. A

c = A B

oldal pedig akkor lesz minimális, ha

B A ⊥ A D

. A szerkesztés következő lépése tehát: a

B

-ből a

\frac{γ}{2}

szög megszerkesztett szárára bocsátott merőleges metszi ki az utóbbiból a keresett

A

csúcspontot. A szerkesztés befejező része: az

A D

szakaszt merőlegesen felező egyenes, amely fentiek szerint párhuzamos

A B

-vel, metszi ki

B D

-ből a

C

csúcspontot, amely e szerint felezőpontja a

B D

-nek, vagyis

a = b

II. megoldás: Az előbbiek alapján a legegyszerűbb szerkesztés a következő: a

C

csúcspontú

γ

szög száraira rámérjük a

\frac{d}{2} = C A = C B

távolságot (2. ábra).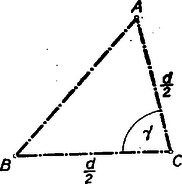

2. ábra

A II. forduló feladatai

1. feladat. Legyen

\begin{matrix} a + b + c & = 0, & (1) \\ A + B + C & = 0, & (2) \\ \frac{a}{A} + \frac{b}{B} + \frac{c}{C} & = 0 & (3) \end{matrix}

Mennyi az

\begin{matrix} a A^{2} + b B^{2} + c C^{2} \end{matrix}

kifejezés értéke?

I. megoldás: Jelöljük a keresett kifejezés értékét

X

-szel. Mivel (2) alapján

A = - (B + C)

B = - (A + C)

és

C = - (A + B)

, azért

\begin{matrix} X = a A^{2} + b B^{2} + c C^{2} = - [a A (B + C) + b B (A + C) + c C (A + B)] = \\ = - a A B - a A C - b B A - b B C - c C A - c C B = \\ = - A B (a + b) - B C (b + c) - C A (c + a) . \end{matrix}

De (1)-ből

a + b = - c

b + c = - a

c + a = - b

, és így a keresett

\begin{matrix} X = A B c + a B C + A b C = A B C (\frac{a}{A} + \frac{b}{B} + \frac{c}{C}) . \end{matrix}

A zárójelben lévő kifejezés értéke (3) alapján

0

, tehát

\begin{matrix} X = 0. \end{matrix}

II. megoldás: Kiindulhatunk az (1)-ből, amely szerint

a = - (b + c)

b = - (a + c)

és

c = - (a + b)

. Tehát

\begin{matrix} X & = a A^{2} + b B^{2} - c C^{2} = - (b + c) A^{2} - (a + c) B^{2} - (a + b) C^{2} = \\ = - a (B^{2} + C^{2}) - b (A^{2} + C^{2}) - c (A^{2} + B^{2}) = \\ = - a {(B + C)}^{2} - b {(A + C)}^{2} - c {(A + B)}^{2} + 2 a B C + 2 b A C + 2 c A B . \end{matrix}

De (3)-ból

A B C

-vel szorozva (

A

B

és

C

nem lehet

0

\begin{matrix} a B C + b A C + c A B = 0, \end{matrix}

(2)-ből

\begin{matrix} {(B + C)}^{2} = A^{2}, {(A + C)}^{2} = B^{2}, {(A + B)}^{2} = C^{2}, \end{matrix}

és így

\begin{matrix} X = - a A^{2} - b B^{2} - c C^{2} = - X, \end{matrix}

amiből

\begin{matrix} X = 0. \end{matrix}

III. megoldás:

(A + B + C) (a A + b B + c C) = 0

, mert az első tényező (2) alapján

0

. A baloldalt átalakítva és az (1) alatti egyenletet figyelembe véve

\begin{matrix} a A^{2} + b B^{2} + c C^{2} + A B (a + b) + B C (b + c) + C A (c + a) = \\ = X - A B c - B C a - C A b = 0. \end{matrix}

(3) alapján a baloldal utolsó három tagjának összege

0

(lásd II. megoldást) és így

\begin{matrix} X = 0. \end{matrix}

2. feladat. Szerkesszünk húrnégyszöget az oldalaiból, ha két szomszédos oldala egyenlő.

I. megoldás: Adva van az

A B C D

húrnégyszögnek

A B = A D = a

B C = b

és

C D = c

oldala. Képzeljük a feladatot megoldottnak (1. ábra).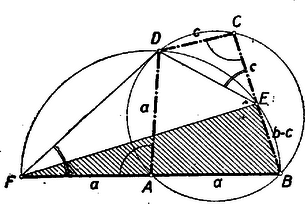

1. ábra

A

körül

A B = A D = a

sugárral rajzolt kör kimetszi a

B C

oldalból, vagy annak meghosszabbításából az

E

pontot, az

A B

oldal meghosszabbításából az

F

pontot. Ismeretes, hogy a húrnégyszögnek bármely szöge egyenlő a szemközti szög mellékszögével. Eszerint tehát a

C

-nél fekvő egy íves szög egyenlő az

A

-nál fekvő egy íves szöggel és az

F B E D

húrnégyszögben az

F

-nél fekvő két íves szög egyenlő a

E

-nél fekvő két íves szöggel. Ebből következik, hogy a

D A F

és

D C E

háromszögek 2‐2 szöge egyenlő, vagyis e két háromszög hasonló. De

A D = A F = a

, és így

C D = C E = c

, vagyis

B E = b - c

. Thales tétele értelmében

B E F ∢ = 90^{\circ}

.
Az

F B = 2 a

átfogóból és

B E = b - c

befogóból a

B E F

derékszögű háromszög (az 1. ábrán srafozva) egyszerűen megszerkeszthető, feltéve, hogy

2 a > b - c

. A

B E F

derékszögű háromszög birtokában az

A

C

és

D

pontok megszerkesztése már nem okoz nehézséget.

II. megoldás: Képzeljük a feladatot megoldottnak. A jelöléseket megtartva, forgassuk az

A D C ▵

-et

A

pont körül úgy, hogy a

D

pont

D'

elforgatása

B

-be kerüljön (2. ábra).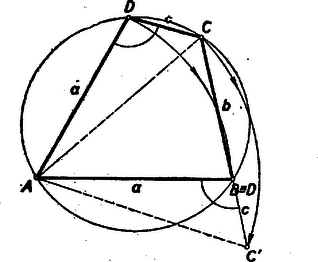

2. ábra

Mivel húrnégyszögünk egy íves

D ∢

-e egyenlő a szemközti

B ∢

egy ívvel jelzett mellékszögével, azért a

C

pont elforgatása,

C'

C B

oldal meghosszabbítására kerül. Mivel

A C = A C'

, azért az

A

pont egyrészt rajta van a

C C'

távolságot merőlegesen felező egyenesen, másrészt pedig a

B

középpontú

a

sugarú körön. A szerkesztést a 3. ábra mutatja.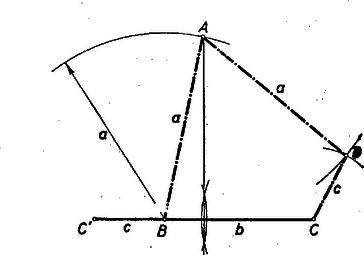

3. ábra

Megoldás van, ha

a > \frac{b - c}{2}

, vagyis

2 a > b - c

III. megoldás: Képzeljük a feladatot megoldva és használjuk az eddigi jelöléseket. Nem megy az általánosság rovására, ha feltesszük, hogy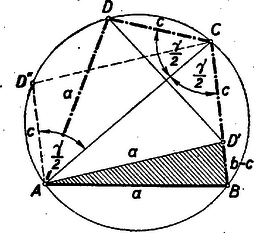

b > c

(4. ábra).

4. ábra

A B = A D

, tehát a fölöttük levő

C

-t nem tartalmazó körívek is egyenlők. Így a kerületi szögek tétele alapján a

C A

átló felezi a

C

-nél fekvő

γ

szöget, tehát a

D

pontnak az

A C

átlóra vonatkozó tükörképe

D'

ráesik a

b

oldalra és

B D' = b - c

. (

D'

tehát azonos az I. megoldásban szerepelt

E

ponttal). Az

A B D'

egyenlőszárú háromszög (a 4. ábrán srafozva) az

a

és

b - c

szakaszokból könnyen megszerkeszthető. (E háromszögnek a keresett húrnégyszöggé való kiegészítése már triviális.)
Lényegében ugyanennek a háromszögnek megszerkesztésére vezet, ha

D

-nek megszerkesztjük az

A C

átlót merőlegesen felező egyenesre vonatkozó

D''

tükörképét (4. ábra). Mivel a

C A D'' ∢

a tükrözés folytán

\frac{γ}{2}

, azért a váltószögek törvénye alapján

A D'' ∥ B C

, vagyis

B C D'' A

egyenlőszárú trapéz, amely az adatokból (

a

szár,

b ∥ c

) szerkeszthető. A szerkeszthetőség feltétele, hogy

2 a > b - c

3. feladat. Három természetes számról a következőket tudjuk:
a) mind a három szám különböző;
b) összegük

406

;
c) legnagyobb közös osztójuk

2

-nél nagyobb törzsszám (jelöljük

p

-vel)
d) ha az egyes számokat elosztjuk p-vel ismét

3

törzsszámot kapunk (legyenek ezek

p_{1}

p_{2}

p_{3}

).
Melyek ezek a számok? Megjegyezzük, hogy

1

nem törzsszám.

Megoldás: A feladat szerint

\begin{matrix} p p_{1} + p p_{2} + p p_{3} = I (p_{1} + p_{2} + p_{3}) = 406 = 2 \cdot 7 \cdot 29, \end{matrix}

ahol

\begin{matrix} p > 2, és 1 < p_{1} < p_{2} < p_{3} . \end{matrix}

Tehát

p = 7

, vagy

p = 29

.
Ha

p = 7

, akkor

p_{1} + p_{2} + p_{3} = 2 \cdot 29 = 58

3

törzsszám összege csak úgy lehet páros, ha egyikük (nyilván a legkisebbik) közülük

2

.
Tehát

p_{1} = 2

, és így

\begin{matrix} p_{2} + p_{3} = 56. \end{matrix}

Ezt az egyenlőséget csak a következő három törzsszámpár egyenlíti ki:

\begin{matrix} 3 + 53, 13 + 43 és 19 + 37. \end{matrix}

p = 29

, akkor

p_{1} + p_{2} + p_{3} = 2 \cdot 7 = 14

. Mivel szükségképpen most is

p_{1} = 2

, azért

\begin{matrix} p_{2} + p_{3} = 12, \end{matrix}

mely esetben csak az

5 + 7

törzsszámpár felel meg.
Tehát összesen 4 megoldás van:

\begin{matrix} \begin{matrix} 14, & 21, & 371; \\ 14, & 91, & 301; \\ 14, & 133, & 259; \\ 58, & 145, & 203. \end{matrix} \end{matrix}

A haladók versenyén kitűzött feladatok megoldását a jövő számunkban közöljük.