Kezdőlap


Cím:	Az 1954. évi Rákosi Mátyás matematikai tanulmányi verseny II. (döntő) fordulója
Füzet:	1954/szeptember, 1 - 12. oldal	PDF \| MathML
Témakör(ök):	OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A II. (döntő) fordulóban, mely április 20-án folyt le, 123 iskola tanulói 287 dolgozatot adtak be. Öt órai munkaidő állott rendelkezésre az alábbi három feladat megoldására:
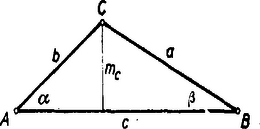
1. Egy háromszög egyik szöge $α = 43^{\circ}$ . Határozzuk meg a háromszög szögeit, ha a háromszög $t$ területére fennáll a

\begin{matrix} 2 t = a b \sqrt[]{sin^{2} α + sin^{2} β + sinα sinβ} \end{matrix}

összefüggés.
2. Egy osztály tanulói között diót osztottak szét. Az első tanuló kapott

a

számú diót és még a megmaradó diók 30-ad részét; a második tanuló

2 a

diót és a még megmaradó diók 30-ad részét; a harmadik tanuló

3 a

diót és a még megmaradó diók 30-ad részét és így tovább. Bizonyítsuk be, hogy ha az első két tanuló egyenlő számú diót kapott, akkor valamennyien ugyanannyi diót kaptak. Mekkora ez esetben az osztály létszáma?
3. Legyenek valamely hegyesszögű háromszög

M

magasságpontjának az oldalakra vonatkozó tükörképei rendre

M_{1}

M_{2}

M_{3}

. Bizonyítsuk be, hogy az

M_{1} M_{2} M_{3}

háromszög és az adott háromszög oldalainak metszéspontjaiból alkotott konvex hatszög szemközti csúcsait összekötő átlók az

M

ponton mennek át.

A Központi Versenybizottság május 20-án a következő jelentést fogadta el:

≫

A Bizottság megállapítja, hogy a verseny több szempontból igen sikeresnek bizonyult.
A feladatok kiválasztása szerencsésnek mondható. Mindegyik bőven adott alkalmat többletmunkára. Főleg a 3. feladat nyújtott sokféle igen ötletes és szellemes megoldásra lehetőséget, amellyel a versenyzők éltek is. A legnehezebbnek bizonyult 2. feladatot is sokan megoldották. Szép számmal vannak olyanok, akik csak az 1. illetőleg csak a 3. feladattal nem tudtak megbirkózni, ezzel szemben sokan vannak. akik viszont csak az 1., vagy csak a 3. feladatot oldották meg. Ez mutatja, hogy bár a feladatok nem voltak túl nehezek, mégis mindegyik megoldása jó készséget igényelt.
Ennek megfelelően a beadott dolgozatok általános értéke is felülmúlja az előző két verseny eredményét. Ebben a feladatok megválasztásán túl komoly része van annak is, hogy haladás észlelhető a versenyzők tudásában és fogalmazásában. Főleg örvendetes, hogy egyre több versenyző akad, aki általánosítások, többféle megoldások megadása, vagy egyéb megjegyzések által igyekszik teljesítményét fokozni.
Természetesen, azért még sok tipikus hiba akad. Az 1. feladatban még sokan feleslegesen logaritmussal, illetőleg szögfüggvények értékének behelyettesítésével dolgoztak, a 2. feladatban sokan csak az utolsó kérdésre feleltek és a feladat lényegéről, a bizonyításról egyáltalán megfeledkeztek, illetőleg egyszerű indukcióval próbáltak bizonyítani teljes indukció helyett. Szép számmal voltak olyanok akik a 3. feladatban a bizonyítandóval egyenértékű állításból indultak ki, vagy bizonyítás közben használtak fel ilyen állítást. Elég gyakran találunk még homályos vagy kevés szövegezést, illetőleg zavaros bőbeszédűséget.
Mindhárom feladatot kifogástalanul megoldotta és azonfelül értékes többletmunkát teljesített 13 tanuló. Ezek közül is elsősorban Vigassy József emelkedik ki, akinek mindhárom megoldása egyszerű és rövid, továbbá az 1. feladathoz fűzött megjegyzése, valamint a 2. feladat általánosításán felül a 3. feladathoz ad egy II. megoldást, amely a legeredetibb és legszebb a versenyen, és általánosítja a 3. feladatot tompaszögű háromszögre. A Bizottság javasolja, hogy az 1. díjat Vigassy József-nek ítéljék oda.
Bártfai Pál és Tomor Benedek dolgozatai már elmaradnak e dolgozat mögött. Utóbbinak teljesítménye mennyiségileg ugyan azonos az első díjra javasolt dolgozatéval, de a 3. feladat II. megoldása elég szürke, míg előbbiében hiányzik a 3. feladat említett általánosítása, de a 3. feladathoz olyan II. és III. megoldásokat tartalmaz, melyek ha nem is vetekszenek Vigassy fent említett megoldásával, mégis értékesek. Megemlítendő még Tomor Benedek szabatos fogalmazása. A Bizottság javasolja, hogy Bártfai Pál és Tomor Benedek egy-egy 2. díjban részesüljön.
Az első csoportba tartozó további 10 dolgozat szerzőit (amely dolgozatok legjobbjai nagyon megközelítik a 2. díjasokét) I. dicséretre ajánlja. II. dicséretre a Bizottság 17 versenyzőt ajánl, akik mindhárom feladatot lényegében megoldották, vagy ezzel egyenértékű teljesítményt nyújtottak. Két feladat megoldásán felül többletteljesítményt ért el 22 versenyző, két feladatot helyesen oldott meg, vagy ezzel egyenértékű teljesítményt nyújtott 18 versenyző. A Bizottság az előbbieket III., az utóbbiakat IV. dicséretre javasolja. Végül a szakérettségis tanulók közül elért jó eredményéért könyvjutalomra javasolja Kovács Istvánt.

≪

Az O. M. a Központi Bizottság javaslata alapján a következő döntést hozta:

1. díj (oklevél és 1000,- Ft. pénzjutalom):
Vigassy József (Bp. I., Petőfi g. IV. o. t )

2. díj (oklevél és 500,- Ft. pénzjutalom):
Bártfai Pál (Bp. I., Petőfi g. III. o. t.);
Tomor Benedek (Győr, Révai Miklós g. IV. o.t.)

I. dicséretben és nagyobb könyvjutalomban részesült:
Balatoni Ferenc (Bp. III., Árpád g. IV. o. t.),
Beleznay Ferenc (Bp. VIII., Piarista g. III. o. t.),
Marik Miklós (Bp. II., Fürst g. IV. o. t.),
Papp Zoltán (Sárospatak, Rákóczi g. IV. o. t.),
Pátkai György (Bp. IX , Fáy A. g. III. o. t.).
Quittner Pál (Bp. I., Petőfi g. III. o. t.),
Reichlin-M. Viktor (Bp. VIII., Piarista g. IV. o. t.),
Siklósi Péter (Sopron, Széchenyi g. IV. o. t.),
Solymoss Otmár (Kőszeg, Jurisich M. g. IV. o. t.),
Zawadowski Alfréd (Bp. I., Petőfi g. IV. o. t.).

II. dicséretet és könyvjutalmat nyert:

Bauer András (Bp. II., Rákóczi g. III. o.t.), Biczó Géza (Bp. II., Rákóczi g. III. o. t.), Csanády Mihály (Esztergom, I. István g. IV. o. t.), Eördögh László (Bp. VIII., Apáczai Csere g. IV. o.t.), Fábián Egon (Bp. XI., József A. g. IV. o. t.), Jámbor Imre (Zalaegerszeg, Zrínyi M. g. IV. o. t.), Kása István (Bp. IX., Fáy g. III. o. t.), Kovács László (Debrecen, Ref. g. IV. o. t.), Lábos Elemér (Sátoraljaújhely, Kossuth g. III. o. t.), Lackner Györgyi (Bp. V., Fonóip. techn. III. o. t.), Lőw Miklós (Bp. VIII., Vörösmarty g. IV. o. t.), Molnár István (Debrecen, Ref. g. IV. o. t.), Németh Lehel (Jászberény, Mikszáth g. IV. o. t.), Sélley Gábor (Bp. X., I. László g. IV. o. t.), Schmidt Eligius (Bp. I., Fürst g. IV. o. t.), Tarlacz László (Szombathely, Nagy Lajos g. III. o.t.), Uray László (Bp. VIII., Piarista g. III. o.t.).

III. dícséretben és könyvjutalomban részesült:

Alexander Gábor (Bp. XIV., I. István g. IV. o. t.), Bagi András (Bp. VIII., Apáczai Csere g. IV. o. t.), Bódás Péter (Székesfehérvár, József A. g. IV. o.t.), Burger Péter (Bp. VII., Madách g. IV. o. t.), Csernyák László (Kaposvár, Táncsics g. IV. o. t.), Csemniczky János (Vác, Gépészeti techn. IV. o. t.), Ehrenfeld János (Bp. VIII., Erőműgép. techn. IV. o. t.), Gergely Péter (Bp. VIII., Apáczai Csere g. IV. o.t.), Gömöry Pál (Bp. I., Fürst g. IV. o. t.), Grätzer György (Bp. VI., Kölcsey g. IV. o. t.), Kertész Ádám (Bp. I., Fürst g. III. o. t.), Masszi György (Pécs, Janus Pannonius g. IV. o. t.). Radda György (Pannonhalma, Bencés g. IV. o. t.), Rippel Géza (Bp. VIII., Vörösmarty g. IV. o. t.), Sántha Ernő (Bp. IX., Fáy g. III. o. t.), Szabó Endre (Gyöngyös, Vak Bottyán g. III. o. t ), Szlanka Imre (Aszód, Petőfi g. III. o. t.), Tolnai Tibor (Szombathely, Nagy Lajos g. III. o. t.), Tóth Dezső (Vác, Sztáron g. IV. o. t.), Varga János (Keszthely, Vajda J. g. IV. o. t.), Vértes Péter (Bp. Eötvös g. III. o. t.), Zarka Sándor (Bp. IX., Fáy g. III. o. t.).

IV. dicséretben és könyvjutalomban részesült:

Balogh György (Székesfehérvár, Magasép. techn. III. o. t.), Bárdos András (Bp. II., Rákóczi g. IV. o. t.), Beczner Kálmán (Bp. VIII., Vörösmarty g. IV. o.t.), Bonyhárd Péter (Bp. VIII., Apáczai Csere g. III. o. t.), Brunner György (Bp. V., Eötvös g. IV. o. t.), Doroszlai Pál (Bp. I., Petőfi g. III. o. t.), Gaál István (Csorna, Latinka g. IV. o. t.), Gelencsér Piroska (Bp. VIII., Zrínyi Ig. III. o. t.), Jónás József (Gyöngyös, Vak Bottyán g. III. o.t.), Kézdy Pál (Bp. II., Rákóczi g. IV. o. t.), Kirz János (Bp. VIII., Apáczai Csere g. III. o. t.), Lőcs Gyula (Bp. V., Eötvös g. IV. o. t.), Pasitka Bálint (Szeged, Vegyip. techn. III. o. t.), Pejtsik Árpád (Bp. VIII., Vörösmarty g. IV. o. t.), Rédei András (Bp. IX., Fáy g. III. o. t.), Roboz Ágnes (Bp. VI., Varga Katalin lg. III. o. t.), Szentai Endre (Bp. VI., Kölcsey g. III. o. t.), Szepesszentgyörgyi Oszkár (Sátoraljaújhely, Kossuth g. III. o. t.).

Könyvjutalomban részesült:

Kovács István (Kecskemét, Ságvári E. szakéretts. tanfolyam.)

A teljesítmények összehasonlítására szerkesztőségünk célszerűnek látja az 1. és 2. díjat 6, ill. 5 ponttal, a négyféle dicséretet pedig rendre 4, 3, 2 és 1 ponttal számítani. (Hangsúlyozzuk, hogy hivatalosan semmiféle pontozás nincs!) Így összesen

6 + 2 \cdot 5 + 10 \cdot 4 + 17 \cdot 3 + 22 \cdot 2 + 18 \cdot 1 = 169

pont került kiosztásra. A verseny végeredményét megyék és iskolafajok szerint az 4. oldalon közölt táblázat mutatja.
Örömmel állapítjuk meg, hogy a 70 kitüntetésben részesült versenyző közül 53-an (75,6%) lapunk feladatmegoldói. Az első 30 helyezett közül 28-an munkatársai lapunknak, akik közül 23-nak az arcképét is közölte a K. M. L. (Részletes beszámoló ‐ sokféle szempontból ‐, a

≫

Köznevelés

≪

augusztus 15-i számában, a 279 ‐ 280. oldalon található.)

Kimutatás az 1954. évi Rákosi Mátyás matematikai verseny II. fordulójáról megyék és iskolafajok szerint

\begin{matrix} Beadott & Kitüntetésben részesültek & Pontszám (nem hivatalos) \\ Megyék és & dolg. száma & Díj & Dicséret & gimn. & ip. t. & Összesen \\ Budapest & isk. & tan. & isk. & tan. & 1 & 2 & I & II & III & IV & isk. & pont & isk. & pont & isk. & pont \\ Baranya & 5 & 7 & 1 & 1 & ‐ & ‐ & ‐ & ‐ & 1 & ‐ & 1 & 2 & ‐ & ‐ & 1 & 2 \\ Bács-Kiskun^{1} & 6 & 10 & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ \\ Békés & 1 & 2 & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ \\ Borsod & 9 & 11 & 2 & 3 & ‐ & ‐ & 1 & 1 & ‐ & 1 & 2 & 8 & ‐ & ‐ & 2 & 8 \\ Csongrád & 4 & 6 & 1 & 1 & ‐ & ‐ & ‐ & ‐ & ‐ & 1 & ‐ & ‐ & 1 & 1 & 1 & 1 \\ Fejér & 4 & 6 & 2 & 2 & ‐ & ‐ & ‐ & ‐ & 1 & 1 & 1 & 2 & 1 & 1 & 2 & 3 \\ Győr-Sopron & 6 & 22 & 4 & 4 & ‐ & 1 & 1 & ‐ & 1 & 1 & 4 & 12 & ‐ & ‐ & 4 & 12 \\ Hajdú-Bihar & 7 & 17 & 1 & 2 & ‐ & ‐ & ‐ & 2 & ‐ & ‐ & 1 & 6 & ‐ & ‐ & 1 & 6 \\ Heves & 3 & 8 & 1 & 2 & ‐ & ‐ & ‐ & ‐ & 1 & 1 & 1 & 3 & ‐ & ‐ & 1 & 3 \\ Komárom & 4 & 5 & 1 & 1 & ‐ & ‐ & ‐ & 1 & ‐ & ‐ & 1 & 3 & ‐ & ‐ & 1 & 3 \\ Nógrád & 3 & 8 & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ \\ Pest & 4 & 5 & 3 & 3 & ‐ & ‐ & ‐ & ‐ & 3 & ‐ & 2 & 4 & 1 & 2 & 3 & 6 \\ Somogy & 2 & 3 & 1 & 1 & ‐ & ‐ & ‐ & ‐ & 1 & ‐ & 1 & 2 & ‐ & ‐ & 1 & 2 \\ Szabolcs-Szatmár & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ \\ Szolnok & 6 & 11 & 1 & 1 & ‐ & ‐ & ‐ & 1 & ‐ & ‐ & 1 & 3 & ‐ & ‐ & 1 & 3 \\ Tolna & 4 & 6 & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ & ‐ \\ Vas & 5 & 7 & 2 & 3 & ‐ & ‐ & 1 & 1 & 1 & ‐ & 2 & 9 & ‐ & ‐ & 2 & 9 \\ Veszprém & 6 & 11 & 1 & 1 & ‐ & ‐ & ‐ & ‐ & 1 & ‐ & 1 & 2 & ‐ & ‐ & 1 & 2 \\ Zala & 2 & 2 & 1 & 1 & ‐ & ‐ & ‐ & 1 & ‐ & ‐ & 1 & 3 & ‐ & ‐ & 1 & 3 \\ Vidék & 81 & 147 & 22 & 26 & ‐ & 1 & 3 & 7 & 10 & 5 & 19 & 59 & 3 & 4 & 22 & 63 \\ Budapest & 42 & 140 & 18 & 44 & 1 & 1 & 7 & 10 & 12 & 13 & 16 & 101 & 2 & 5 & 18 & 106 \\ Összesen & 123 & 287 & 40 & 70 & 1 & 2 & 10 & 17 & 22 & 18 & 35 & 160 & 5 & 9 & 40 & 169 \end{matrix}

Alább közöljük a II. forduló feladatainak megoldását.

1. feladat.
A megoldás lényege annak észrevétele volt, hogy a feltételi egyenletből következik, hogy a

γ

szög értéke

120^{\circ}

. Ehhez lényegében két úton juthatunk: vagy a szögeket küszöböljük ki távolságok segítségével és azután felhasználjunk a háromszög alkotórészei közötti összefüggéseket, vagy az adott összefüggést goniometriai összefüggéssé igyekszünk alakítani és goniometriai átalakításokat végzünk. Az előbbi út pl. a következő módon követhető.

I. megoldás: A betűzést az ábra mutatja. Helyettesítsük be az adott összefüggésbe a

sin α = \frac{m_{c}}{b}, sin β = \frac{m_{c}}{a}, 2 t = c m_{e}

kifejezéseket és emeljünk négyzetre. Mivel mindkét oldalon pozitív mennyiség áll, az eredetivel ekvivalens összefüggéshez jutunk

\begin{matrix} c^{2} m_{c}^{2} = a^{2} b^{2} (\frac{m_{c}^{2}}{a^{2}} + \frac{m_{c}^{2}}{b^{2}} + \frac{m_{c}^{2}}{a b}) = (a^{2} + b^{2} + a b) m_{c}^{2} . \end{matrix}

Innen, mivel

m_{c}

nem lehet 0 (

α = 43^{\circ}

folytán a háromszög nem lapulhat egyenes szakasszá),

\begin{matrix} c^{2} = a^{2} + b^{2} + a b . \end{matrix}

(1)

Másrészt a cosinus-tétel szerint

\begin{matrix} c^{2} = a^{2} + b^{2} - 2 a b cos γ \end{matrix}

A két kifejezést összehasonlítva

cos γ = - \frac{1}{2}

, tehát

γ < 180^{\circ}

miatt

γ = 120^{\circ}

lehet csak és ebben az esetben (1), s így az eredeti összefüggés is valóban teljesül. Ez esetben

α + β = 60^{\circ}

, tehát a háromszög szögei

α = 43^{\circ}

β = 17^{\circ}

γ = 120^{\circ}

II. megoldás: Felhasználva a terület meghatározására szolgáló

2 t = a b sin γ

összefüggést, a 0-tól különböző

a b

-értékkel osztva és négyzetre emelve kapjuk, hogy

\begin{matrix} sin^{2} γ = sin^{2} α + sin^{2} β + sin α sin β, \end{matrix}

(2)

vagy

\begin{matrix} sin^{2} α + sin^{2} β - sin^{2} γ + sin α sin β = 0. \end{matrix}

Alakítsuk át először a középső különbséget, szögfüggvények összegének és különbségének szorzatalakját használva [ehelyett a

sin γ = sin (α + β)

kifejezés tagokra bontásával is célhoz érhetnénk]

\begin{matrix} sin^{2} β - sin^{2} γ = (sin β + sin γ) (sin β - sin γ) = \\ = 2 sin \frac{β + γ}{2} cos \frac{β - γ}{2} \cdot 2 cos \frac{β + γ}{2} sin \frac{β - γ}{2} = \\ = 2 sin \frac{β + γ}{2} cos \frac{β + γ}{2} \cdot 2 sin \frac{β - γ}{2} cos \frac{β - γ}{2} = \\ = sin (β + γ) sin (β - γ) = sin α sin (β - γ) . \end{matrix}

Ezt felhasználva

\begin{matrix} sin^{2} α + sin^{2} β - sin^{2} γ + sin α sin β = sin α [sin α + sin (β - γ)] + sin α sin β = \\ = 2 sin α sin \frac{α + β - γ}{2} cos \frac{α - β + γ}{2} + sin α sin β = \\ = 2 sin α sin \frac{180^{\circ} - 2 γ}{2} cos \frac{180^{\circ} - 2 β}{2} + sin α sin β = \\ = 2 sin α sin (90^{\circ} - γ) \cdot cos (90^{\circ} - β) + sin α sin β = \\ = 2 sin α sin β cos γ + sin α sin β = 2 sin α sin β (cos γ + \frac{1}{2}) . \end{matrix}

E szorzat csak úgy lehet 0, ha

cos γ = - \frac{1}{2}

, azaz

γ = 120^{\circ}

Megjegyzések: 1. A II. megoldásban a lapunk 560. feladalaban (VIII. köt. 82. old.) szereplő

\begin{matrix} sin^{2} α + sin^{2} β - sin^{2} γ = 2 sin α sin β cos γ, ha α + β + γ = 180^{\circ} \end{matrix}

(3)

azonosságot bizonyítottuk be és alkalmaztuk. Többen fel is használták készen ezt az azonosságot a megoldáshoz.
2. Néhányan a (2) összefüggésből jutottak (1)-hez, felhasználva a sinustételt az

\frac{a}{sin α} = \frac{b}{sin β} = \frac{c}{sin γ} = λ

alakban, vagy pontosabban az

a = 2 r sin α

stb. összefüggéseket, ahol

r

a háromszög köré írt kör sugara. Ugyanezen az úton a cosinus-tétel is goniometriai összefüggéssé alakítható, éppen a (3) azonossággá, és (2)-vel összehasonlítva adja a kívánt eredményt.

2. feladat.

I. megoldás: Legyen a szétosztandó diók száma

d

, ekkor az első tanuló

\begin{matrix} a + \frac{d - a}{30} = \frac{d}{30} + \frac{29}{30} a \end{matrix}

diót kap, a másodiknak jutó diók mennyisége pedig

\begin{matrix} 2 a + \frac{d - \frac{d}{30} - \frac{29}{30} a - 2 a}{30} = \frac{29}{30^{2}} d + (2 \frac{29}{30} - \frac{29}{30^{2}}) a = \frac{29}{30^{2}} d + \frac{29 \cdot 59}{30^{2}} a . \end{matrix}

Ha tehát az első két tanuló ugyanannyi diót kapott, akkor

\begin{matrix} \frac{d}{30} + \frac{29}{30} a = \frac{29}{30^{2}} d + \frac{29 \cdot 59}{30^{2}} a, azaz \frac{d}{30^{2}} = \frac{29^{2}}{30^{2}} a, d = 29^{2} a, \end{matrix}

és az első két tanuló egyenként

\begin{matrix} a + \frac{d - a}{30} = a + \frac{(29^{2} - 1) a}{30} = a + \frac{28 \cdot 30}{30} a = 29 a \end{matrix}

diót kapott. Teljes indukcióval bizonyitjuk, hogy a többinek is ugyanennyi dió jut. Legyen

k > 2

és tegyük fel, hogy már az első

k - 1

tanulóról beláttuk, hogy nekik egyenként

29 a

dió jutott. Ekkor maradt meg

d - (k - 1) 29 a = 29 (30 - k) a

dió, így a

k

-adik tanulónak

\begin{matrix} k a + \frac{29 (30 - k) a - k a}{30} = \frac{30 k a + 29 \cdot 30 a - 29 k a - k a}{30} = 29 a \end{matrix}

dió jut. Így valóban sorban minden diák

29 a

diót kap. Ennek folytán

29 a^{2}

számú dióból 29 diáknak tudunk adni, tehát 29-en vannak az osztályban.

Megjegyzés: Szó szerint ugyanilyen meggondolással látható, hogy ha nem 30-ad részét, hanem tetszésszerinti

b

-ed részét (

b > 1

) vesszük mindig a maradéknak, akkor

d^{2} = {(b - 1)}^{2} a

számú diónak kell kezdetben lennie ahhoz, hogy az első és a második diáknak ugyanannyi dió jusson, ekkor mindegyiküknek, és velük együtt a további diákoknak is (

b - 1) a

dió jut, egészen a

(b - 1)

-edikig, aki megkapja az összes még meglévő diót. A feladat további általánosítása lesz leolvasható a következő megoldásból.

II. megoldás: Legyen a kiosztandó diók száma

d

, kapjon a

k

-adik tanuló

k a

diót és még a maradék

b

-ed részét, a

k

-adik tanulónak jusson ilyen módon

c^{k}

dió és legyen a visszamaradó diók száma

d_{k}

, jelentse

d_{0}

d

-t. Ekkor

\begin{matrix} d_{k - 1} = c_{k} + d_{k} k = 1,2, ... . \end{matrix}

(1)

és

\begin{matrix} c_{1} = a + \frac{d - a}{b} = \frac{b}{d} + \frac{b - 1}{b} a, c_{2} = 2 a + \frac{d_{1} - 2 a}{b} = \frac{d_{1}}{b} - 2 \frac{b - 1}{b} a, \end{matrix}

általában

\begin{matrix} c_{k} = k a + \frac{d_{k - 1} - k a}{b} = \frac{d_{k = 1}}{b} + k \frac{b - 1}{b} a k = 1,2, ... \end{matrix}

(2)

Vizsgáljuk két egymásutáni tanulónak jutó mennyiség különbségét, használjuk rá a

D_{k} = c_{k + 1} - c_{k}

jelölést:

\begin{matrix} D_{k} = \frac{d_{k} - d_{k - 1}}{b} + \frac{b - 1}{b} a = \frac{b - 1}{b} a - \frac{c_{k}}{b} \end{matrix}

(1) szerint, s igy két szomszédos különbség különbségében már

a

nem fog szerepelni:

\begin{matrix} D_{k + 1} - D_{k} = - \frac{c_{k + 1} - c_{k}}{b} = - \frac{D_{k}}{b}, azaz D_{k + 1} = \frac{b - 1}{b} D_{k} . \end{matrix}

Azt nyertük tehát, hogy a

D_{k}

különbségek mértani sorozatot alkotnak. Ennek hányadosa

\frac{b - 1}{b} > 0

, mert

b > 1

. Eszerint az egymásutáni diákoknak jutó diómenynyiség vagy állandóan csökken, vagy állandóan növekszik, vagy mindannyian egyenlő számú diót kapnak.
A feladat állítása tehát így általánositható: ha van két diák, akik egyenlő mennyiségű diót kaptak, akkor mindenkinek ugyanannyi dió jutott.
Hogy a három eshetőség közül melyik következik be, az

D_{1}

előjelétől, illetve 0 voltától függ. Mivel

\begin{matrix} D_{1} = \frac{b - 1}{b} a - \frac{c_{1}}{b} = \frac{(b - 1) b}{b^{2}} a - \frac{d}{b^{2}} - \frac{b - 1}{b^{2}} a = \frac{{(b - 1)}^{2}}{b^{2}} a - \frac{d}{b^{2}} = \\ = \frac{{(b - 1)}^{2} a - d}{b^{2}} \end{matrix}

tehát az egymásutáni diómennyiségek aszerint nőnek, csökkennek, vagy lesznek egyenlők, amint

\begin{matrix} d < {(b - 1)}^{2} a, vagy d > {(b - 1)}^{2} a, vagy d = {(b - 1)}^{2} a . \end{matrix}

k

-adik tanulónak

\begin{matrix} c_{k} = c_{1} + D_{1} + D_{2} + ... + D_{k - 1} = \end{matrix}

\begin{matrix} = \frac{d}{b} + \frac{b - 1}{b} a + D_{1} [1 + \frac{b - 1}{b} + ... + {(\frac{b - 1}{b})}^{k - 2}] = \\ = \frac{d}{b} + \frac{b - 1}{b} a + \frac{{(b - 1)}^{2} a - d}{b^{2}} \cdot \frac{1 - {(\frac{b - 1}{b})}^{k - 1}}{\frac{1}{b}} = \\ = \frac{d}{b} + \frac{b - 1}{b} a + \frac{{(b - 1)}^{2} a - d}{b} - \frac{{(b - 1)}^{2} a - d}{b} \cdot {(\frac{b - 1}{b})}^{k - 1} \end{matrix}

azaz

\begin{matrix} c_{k} & = \frac{b - 1 + b^{2} - 2 b + 1}{b} a - \frac{{(b - 1)}^{2} a - d}{b} {(\frac{b - 1}{b})}^{k} \frac{b}{b - 1} = \\ = (b - 1) a - \frac{{(b - 1)}^{2} a - d}{b - 1} \cdot {(\frac{b - 1}{b})}^{k} . \end{matrix}

dió jut az általános esetben egészen azon

n

-edik tanulóig, akinek a részét kiadva már

(n + 1) a

diónál kevesebb marad vissza. Ennek feltételéül az általános esetben meglehetősen áttekinthetetlen egyenlőtlenség adódik.

3. feladat.

I. megoldás: A betűzést az 1.ábra mutatja.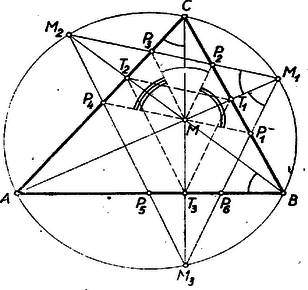

1. ábra

Először egy segédtételt bizonyítunk be. Ismert tétel alapján (Gallai-Péter I. oszt.tankönyv 1953 ‐ 302. old.) az

M_{1}

M_{2}

M_{3}

pontok rajta vannak az

A B C_{Δ}

köré írt körön. Mint merőlegesszárú szögek a

B

-nél levő egyíves szög egyenlő a

C

-nél levő egyíves szöggel, vagyis a kerületi szögek tétele alapján

\hat{M_{2} A} = \hat{A M_{3}}

és így az

M_{1} A

egyenes felezi az

M_{1} M_{2} M_{3 Δ}

M_{1} ∢

-ét. Ugyanez áll az

M_{2} B

és

M_{3} C

egyenesekre is az

M_{2} ∢

, illetőleg

M_{3} ∢

-ge1 kapcsolatban.
Ennek felhasználásával a feladat állítása így bizonyítható: Kössük össze az

M

pontot a keletkezett hatszög

P_{1}

P_{2}

P_{3}

és

P_{4}

csúcspontjaival. Az

M P_{1} M_{1} P_{2}

négyszögben a

P_{1} P_{2}

átló a tükrözés miatt felezi a

P_{1}

és

P_{2}

csúcspontoknál levő szögeket. Tehát a szóban forgó négyszögben a két átló egymásra merőleges és a segédtétel alapján mindkét átló egyúttal szögfelező, amiből következik, hogy az

M P_{1} M_{1} P_{2}

négyszög rombusz, és így

P_{1} M ∥ M_{1} P_{2}

. Hasonlóképpen az

M P_{4} M_{2} P_{3}

rombuszban

P_{4} M ∥ M_{2} P_{3}

.
De az

M_{1} P_{2}

és

M_{2} P_{3}

szakaszok rajta vannak az

M_{1} M_{2}

egyenesen, amellyel a

P_{1} M

és

P_{4} M

szakaszok külön-külön párhuzamosak. A két utóbbi szakasznak egy közős pontja

M

, és így

P_{1}

M

és

P_{4}

egy egyenesen vannak, vagyis a

P_{1} P_{4}

átló átmegy az

M

ponton. Ugyanígy bizonyítható ez a

P_{2} P_{5}

, ill.

P_{3} P_{6}

átlóra is.

Megjegyzés: Igen sok versenyző ‐ a segédtétel nélkül ‐ az átlók merőlegességéből és csak egyedül a

P_{1} P_{2}

átló szögfelező voltából már rombuszra következtetett, megfeledkezvén a deltoidról.

II. megoldás: Segédtételünkhöz a háromszög köré írt kör nélkül is eljuthatunk. Ugyanis, ha az adott

A B C_{Δ}

-nek

T_{1} T_{2} T_{3}

talpponti háromszögét tekintjük (1. ábra), akkor nyilván az

M_{1} M_{2} M_{3 Δ}

a talpponti háromszögnek 2 : 1 arányú nagyítása az

M

hasonlósági centrumból. Elég most már arra az ismert tételre hivatkozni (Gallai-Péter I. oszt. Tankönyv 1953 ‐ 287-288. old.), hogy a háromszög magasságvonalai a talpponti háromszög szögfelezői.
Lényegében ezzel azonos bizonyítás: az

M_{1}, M_{2}

és

M_{3}

pontokon át a

B C

C A

, ill.

A B

oldalakkal húzott párhuzamos egyenesek által alkotott

A_{1} B_{1} C_{1 Δ}

-ben alkalmazzuk a talpponti háromszögre vonatkozó idézett tételt.

III. megoldás: Segédtételünk alapján

P_{2} T_{1} = T_{1} P_{1}

P_{3} T_{2} = T_{2} P_{4}

M_{1} T_{1} = T_{1} M

(1. ábra). Az

M_{1}

P_{2}

és

P_{3}

pontok az

M_{1} M_{2}

egyenesen vannak, a

T_{1} T_{2}

egyenes pedig párhuzamos az

M_{1} M_{2}

egyenessel, azért a

P_{1}

P_{4}

és

M

pontok rajta vannak az

M_{1} M_{2}

egyenesnek a

T_{1} T_{2}

egyenesre vonatkozó tükörképén, vagyis

P_{1}

P_{4}

és

M

egy egyenesen vannak.

IV. megoldás: Jelöljük az

M_{1} M_{2} M_{3 Δ}

szögeit

M_{1} ∢

M_{2} ∢

, ill.

M_{3} ∢

-gel. Mivel ‐ mint láttuk ‐

M P_{1} M_{1} P_{2}

és

M P_{4} M_{2} P_{3}

rombuszok (1. ábra), azért az

M

-nél fekvő két, ill. három ívvel jelölt szögek egyenlők

M_{1} ∢

ill.

M_{2} ∢

-gel. Az

M

-nél fekvő áthúzott ívvel jelölt szög pedig mint megfelelő szög, egyenlő

M_{3} ∢

-gel. Tehát a

P_{1} M P_{4} ∢ = M_{1} ∢ + M_{2} ∢ + M_{3} ∢ = 180^{\circ}

, vagyis

P_{1}

M

és

P_{4}

egy egyenesen van.

V. megoldás: Húzzunk az

M

ponton át párhuzamost az

M_{1} M_{2}

oldallal. Messe ez

M_{1} M_{3}

-at

D

-ben,

M_{2} M_{3}

-at

E

-ben. (2. ábra).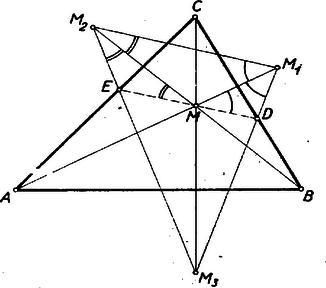

2. ábra

A segédtétel alapján következik, hogy

D M M_{1} ∢ = M M_{1} M_{2} ∢ = M M_{1} M_{3} ∢

, tehát az

M M_{1} D_{Δ}

egyenlőszárú, s így

D

M M_{1}

felező merőlegesén van. E felező mérőleges azonban a

B C

egyenes, tehát

D

M_{3} M_{1}

és

B C

egyenesek metszéspontja, vagyis a hatszög egyik csúcsa

(D = P_{1})

. Hasonlóan következik, hogy

E

C A

és

M_{2} M_{3}

oldalak metszéspontja, amely a hatszögnek

D

-vel átellenes pontja

(E = P_{4})

. Az ezeket összekötő átló tehát valóban

M

-en megy keresztül. Hasonlóan okoskodhatunk a többi átlókkal is. (Lényegében ez a gondolata Pátkai György bizonyításának).
A segédtétel felhasználása nélkül, közvetlenül az

M_{1}

M_{2}

M_{3}

pontokon átmenő kör segítségével is bizonyíthatjuk állításunkat, amint azt a VI ‐ IX. megoldások mutatják.

VI. megoldás: Kössük össze az

M

pontot a hatszög

P_{3}

és

P_{6}

csúcspontjával (3. ábra).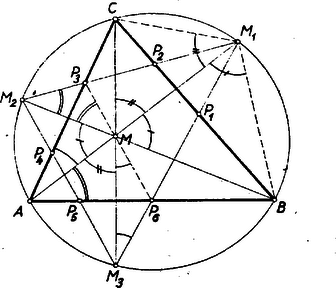

3. ábra

A B M_{1} C

húrnégyszögben

A ∢ + M_{1} ∢ = 180^{\circ}

. Tehát az

A

csúcsnál lévő, az ábrán egy ívvel, ill. két ívvel és az

M_{1}

csúcsnál egyszer áthúzott, ill. kétszer áthúzott ívvel jelölt szögek, (szám szerint 4) összege

180^{\circ}

.
Az

A

-nál levő egyíves szög, mint kerületi szög egyenlő az

M_{3}

-nál lévő egyíves szöggel, ez pedig a tükrözés folytán egyenlő az

M

-nél levő egyíves szöggel. Teljesen ugyanígy bizonyítható, hogy az

A

-nál lévő kétíves szög egyenlő az

M

-nél lévő kétíves szöggel. Az

M_{1}

-nél lévő egyszer áthúzott ívvel jelölt szög, mint tükrös szög, ill. csúcsszög egyenlő az

M

-nél fekvő hasonló jelzésű szöggel. Ugyanez áll az

M_{1}

-nél és

M

-nél lévő kétszer áthúzott ívvel jelölt szögekre is. De a

P_{3} M P_{6} ∢

éppen e négyféle szög összege, vagyis

P_{3} M P_{6} ∢ = 180^{\circ}

. Ezzel bebizonyítottuk, hogy a

P_{3} P_{6}

átló átmegy az

M

ponton. (Tomor Benedek megoldása.)

VII. megoldás: Kössük össze az

M

pontot a hatszög

P_{2}

és

P_{5}

csúcspontjával. Be fogjuk bizonyítani, hogy a

B P_{2} M P_{5}

négyszögben az

M ∢ = 180^{\circ}

(4. ábra).

4. ábra

P_{2}

-nél lévő egyíves szögek a tükrözés miatt egyenlők. Ennek a szögnek pótló szöge az

M_{1}

-nél fekvő kétíves szög, amely, mint kerületi szög, egyenlő a

B

-nél fekvő kétíves szöggel, ez viszont mint merőlegesszárú szög, egyenlő a

C

-nél fekvő kétíves szöggel. Ez utóbbi pótlószöge az

A

-nál fekvő egyíves szögnek. Tehát négyszögünk

P_{2} ∢

-e egyenlő az

A B C_{Δ} A ∢

-ével. Ugyanígy bizonyíthatjuk, hogy négyszögünk

P_{5} ∢

-e(az ábrán egyszer áthúzott ívvel jelölve) egyenlő az

A B C_{Δ} C ∢

-ével. Tehát négyszögünkben

B ∢ + P_{2} ∢ + P_{5} ∢ = B ∢ + A ∢ + C ∢ = 180^{\circ}

, és így a negyedik szög:

M ∢ = 180^{\circ}

. (Bártfai Pál megoldása.)

VIII. megoldás: Kössük össze az

M

pontot a hatszög

P_{3}

és

P_{6}

csúcspontjával (5. ábra).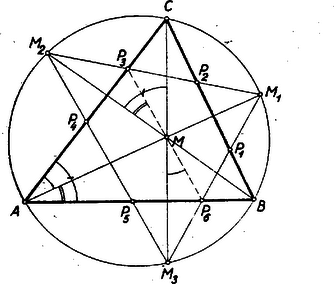

5. ábra

A

-nál fekvő egyíves, ill. kétíves szög a VI. megoldás alapján egyenlő az

M

-nél fekvő hasonló jelzésű szögekkel. E két szög összege az

A

-nál fekvő egyszer áthúzott ívvel jelölt szög, amely mint merőleges szárú szög, egyenlő az

M

-nél fekvő egyszer áthúzott ívvel jelölt szöggel, amiből következik, hogy a

P_{3} M C

egyenlő az egyíves szöggel, vagyis

P_{3} M C ∢

és

P_{6} M M_{3} ∢

csúcsszögek. Tehát a

P_{3} P_{6}

átló átmegy az

M

ponton.

IX. megoldás: Kössük össze az

M

-et a hatszög

P_{1}

és

P_{4}

csúcspontjával, továbbá

C

-t

M_{1}

és

M_{2}

-vel (6. ábra).

6. ábra

M_{1}

-nél lévő egyíves szög a tükrözés folytán egyenlő az

M

-nél lévő egyíves szöggel. Ugyanígy egyenlők az

M_{2}

és

M

-nél lévő kétíves szögek. De az

M_{1} C M_{2} M_{3}

húrnégyszögben a

M_{1} ∢ + M_{2} ∢ = 180^{\circ}

, tehát a

P_{1} M P_{4} ∢ = 180^{\circ}

. (Reichlin-M. Viktor megoldása.)
Az állítás következő, igen szellemes, csupán a talpponti háromszög tulajdonságain alapuló bizonyítását adta Vigassy József, a verseny győztese.

X. megoldás: Kössük össze az

M

pontot a hatszög

P_{3} P_{2} P_{1}

és

P_{6}

csúcsaival, továbbá húzzuk meg az

A B C_{Δ}

-ben az

M

-en át az

A B

-vel párhuzamos

A' B'

és az

A C

-vel párhuzamos

A'' C''

szakaszt (7. ábra).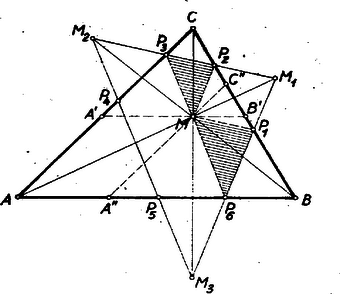

7. ábra

A keletkezett

A' B' C

és

A'' B C''

háromszögek hasonlók és hasonló fekvésűek. A tükrözés folytán az

M P_{3} P_{2}

, ill.

P_{6} M P_{1 Δ}

-ek a fenti két háromszögbe írt minimális kerületű háromszögek (Gallai Péter I. oszt. Tankönyv 1953 ‐ 332-334. old.), vagyis a talpponti háromszögek, melyek tehát egymásközt szintén hasonlók és hasonló fekvésűek. Tehát

M P_{3} ∥ P_{6} M_{1}

, mint megfelelő oldalak. E két párhuzamos szakasznak

M

végpontja közös, ennélfogva a

P_{6}

M

és

P_{3}

pontok egy egyenesbe esnek.

Megjegyzés: Tételünk tompaszögű háromszögre is általánosítható, de akkor a megfelelő

P_{1} P_{2} P_{3} P_{4} P_{5} P_{6}

pontok hurkolt hatszögre vezetnek, melynek kétszeres pontja (hurokpontja) mindenkor a tompaszög csúcspontja. A szemközt fekvő csúcspontok most is a

P_{1}

és

P_{4}

P_{2}

és

P_{5}

P_{3}

és

P_{6}

csúcspontok (8.ábra).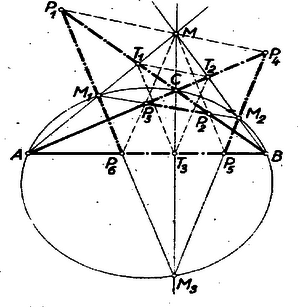

8. ábra

A bizonyítás ugyanúgy történik, minta hegyesszögű háromszög esetén, csakhogy most a tompaszöget bezáró oldalokhoz tartozó magasságok (melyeknek talppontjai az oldalak meghosszabbítására esnek) a talpponti háromszög külső szögét felezik, vagyis a tompaszöget bezáró oldalak felezik a talpponti háromszög megfelelő szögeit. Az

M

hasonlósági centrum e szerepét most is megtartja.

¹1 szakérettségis tanuló könyvjutalomban részesült.