I. A közönséges ‐ más szóval euklideszi ‐ geometriában két pontra, $X$ és $Y$-ra nézve mindig értelmezve van egy nem negatív szám ‐ jelöljük $\varrho \left(XY\right)$-nal ‐, amely szám kielégíti a következő kirovásokat:
1. az azonosság axiómáját: $\varrho \left(XY\right)=0$ akkor és csakis akkor, ha az $X$ és $Y$ pontok azonosak egymással;
2. a szimmetria axiómáját: $\varrho \left(XY\right)=\varrho \left(YX\right)$;
3. a háromszögaxiómát: bármely három $X$, $Y$, $Z$ pontra nézve

A,B,C...XYZ...-vel. Ha teljesülnek az 1‐3. axiomák, akkor a $\Sigma$-t metrikus ponthalmaznak, a $\varrho \left(XY\right)$ számot az $X$ és $Y$ pontok egymástól való távolságának nevezzük.

 

II. Most pedig egy különös példát mutatunk a metrikus ponthalmazra. Tekintsük a végtelen sakktáblát (vagyis az egész síkot hézagtalanul befedő, végtelen sok mezejű sakktáblát). Nevezzük a tábla mezőit pontoknak, továbbá egy mezőről más mezőre vezető lehető legkevesebb lóugrás számát a két pont (vagyis a két mező) egymástól való távolságának. (Egy mezőről önmagára vezető legkevesebb lóugrás száma ugyan 2 ‐ ugrás és annak visszája ‐ azért egy pontnak önmagától való távolságát nem a különböző pontok távolságának mintájára értelmezzük, hanem $0$-nak vesszük.)
A mondott halmaz a benne értelmezett távolság fogalom szerint megfelel az 1‐3. axiómáknak. Ellenőrizzük ennek az állításnak a helyességét.
Először is azt kell megmutatnunk, hogy bármelyik két (különböző) mezeje is a végtelen sakktáblának az $X$ és $Y$, a $\varrho \left(XY\right)$ számot egyértelműen meghatározzák.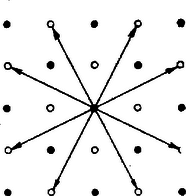

 

 

1. ábra

 

Először is kiválasztunk egy mezőt, $X$-et. Ezt rögzítjük és $Y$ gyanánt vegyük egyenként a sakktábla többi mezejét. (Az 1. ábrán az $X$ szerepét a középső sötét mező játssza.) Írjunk az $X$ mezőre $0$-t. A belőle egyetlen ugrással elérhető mezőket jelöljük meg 1-essel. (8 fehér mező, az 1. ábrán a 8 nyíl vége mutatja a mezőket.) Most ugyanezt az eljárást egymásután hajtsuk végre az 1-essel jelölt mezőkből kiindulva, s jelöljük az elért mezőket 2-sel. Ha már számozott mezőre érkezünk, akkor nem írunk újabb számot a mezőre, hanem megtartjuk a már odaírtat. Most megismételjük a 2-sel jelölt pontokból kiindulva az eljárást és az elért, de még nem számozott mezőket 3-sal megjelöljük. És így tovább.
Az így származtatott számkonfigurációt (az 5-ös mezőkig terjedően) a 2. ábrán mutatjuk be.

 

 

2. ábra

 

(A sakktáblának e számokat tartalmazó mezői sötét-világos színváltakozását nem tüntettük fel, hiszen ha 0-sal sötét mezőt számoztunk, akkor minden páros, ill. páratlan számmal jelölt mező sötét, ill. világos, ezért a színezést mellőzhettük.) E konfiguráció előállítási utasításából nyilvánvaló, hogy bármelyik mezőre írt szám annak a mezőnek a 0-sal jelzettől való lóugrástávolságát jelenti e távolság definíciójának megfelelően.
A számkonfigurációt ‐ az egyedülálló középső mezőtől eltekintve ‐ két mezőnyi szélességű övekre tagoltuk, amelyek ‐ belülről kezdve a számlálást ‐ az 5-ik övtől fogva szabályos számelosztási szerkezetet mutatnak. Nevezetesen azt, hogy az $n$-ik övön túl már $n$-essel jelölt mező nincs (ez már akkor is teljesül, ha $n>2$), az övben pedig a mezők színváltakozásának megfelelően csak $n$ és $\left(n+1\right)$ számok lépnek fel. Ha pedig az $n$- és $\left(n-1\right)$-ik övet egyesítjük (itt már kell az $n>4$ kirovás), akkor a keletkezett 4 mezőnyi szélességű öv az összes $n$-essel jelölt mező tartalmazza, s fellépnek benne még $\left(n+1\right)$-essel) és $\left(n-1\right)$-essel jelölt mezők.
Utolsó állításunk $n=5$-re már helyes voltát megkonstruált számkonfigurációnk, vagyis a 2. ábra bizonyítja. Az $n>5$ esetben pedig a bizonyítás abból áll, hogy ha a tétel valamely $n$ értékre nézve fennáll, akkor abból az $\left(n+1\right)$-re való helyessége is következik. Ilyen $n$ van: $n=5$. Hajtsuk végre a bizonyítást.
Tegyük fel, hogy számkonfigurációnk az $n$-ik övig ki van dolgozva. Ebben az övben a mezők színváltakozása szerint az $n$ és $\left(n+1\right)$ lép fel váltakozva. Tudjuk, hogy az $\left(n-1\right)$-ik övben csak $\left(n-1\right)$ és $n$ számjegyek lépnek fel, s ennek az övnek a külső határvonalán kívül $\left(n-1\right)$-essel jelölt mező nincs. Belső határvonalán belül pedig $n$-essel jelölt mező nincs. Tekintsük most az $\left(n+1\right)$-ik övet. Ebbe az övbe csakis az $n$-ik öv mezőiből lehet egy-egy lóugrással bejutni. Mégpedig bármelyik mezejére és egy lóugrás az $n$-ik övből az $\left(n+1\right)$-ik övön túlra már nem vezet ki.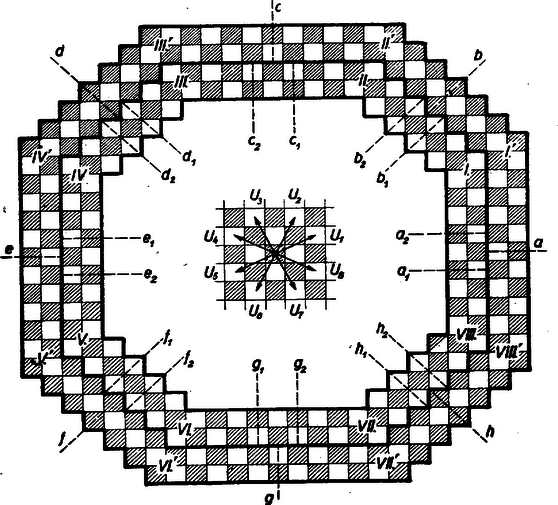

 

 

3. ábra

 

(A 3. ábra éppen az $n$-ik és $\left(n+1\right)$-ik öv helyzetviszonyát szemlélteti. Ha a középső mező világos volna, akkor ugyanazokban az övekben a sötét és világos mezők helyén világos és sötét mezők volnának.)
Minthogy a lóugrás egy mezőről ellentett színű mezőre vezet, s az $n$-ik övben csak $n$ és $\left(n+1\right)$ számok szerepelnek a színek váltakozása szerint, továbbá az $\left(n+1\right)$-ik övbe csakis az $n$-ikből léphetünk egy lóugrással, azért az $\left(n+1\right)$-ik övben ‐ a színek váltakozását követve ‐ csakis az $\left(n+1\right)$ és $\left(n+2\right)$ számok lépnek fel. Csak azt kell még belátnunk, hogy az $\left(n+1\right)$-ik övben nem marad számozatlan mező, vagyis mindegyik mezőre vezet alkalmas lóugrás az $n$-ik öv alkalmas mezejéről.
Pl. a külső öv $a$, $b$ egyenesekkel határolt I$\text{'}$ részébe mindenüvé eljuthatunk a belső öv $a_1$, $b_1$-gyel határolt részéből, ha ennek minden mezejéről egy-egy, $u_1$ irányú lóugrást teszünk. (A részhez a kettészelt mezők is hozzáértendők.) Hasonlóan a többi részre is a megfelelő sorszámú részből a megfelelő számozású irányban tett lólépéssel. Az I$\text{'}-$VIII.$\text{'}$ részek pedig hézagtalanul megtöltik a külső övet. S ezzel az $n>5$-re nézve befejeztük állításunk bizonyítását.
Láttuk, hogy a középső mező körül gyűrűző övek sorozata határtalanul folytatható s a benne fellépő számelrendezés egyértelműen meghatározott processzus. A konfiguráció középső mezeje legyen $X$, egy tetszőleges másik mezeje $Y$. Most $\varrho \left(XY\right)$-on éppen az $Y$ mezőre írt számot értjük.
Az így definiált $\varrho \left(XY\right)$ nyilvánvalóan kielégíti a Fréchet-féle 1. axiómát.
Minthogy minden lóugrás visszája is lóugrás és a lóugrások sorozataként előállított utat a visszája ugrások fordított sorozataként is leírhatjuk (a végponttól a kezdőpontig), könnyen belátható a 2. axióma teljesülése is.
Ha a 3. axióma nem teljesülne, akkor volna olyan 3 mező ‐ $X$, $Y$, $Z$ ‐ hogy azokra nézve fennállna a

$\begin{array}{c}{\displaystyle \varrho \left(XY\right)+\varrho \left(YZ\right)<\varrho \left(XZ\right)\mathrm{.}}\end{array}$

Ez azonban a $\varrho \left(XY\right)$ minimális voltának mondana ellent: vagyis volna a $\varrho \left(XY\right)$-t definiáló, lóugrással leírt útnál kevesebb ugrásból álló is (mely $X$ mezőről $Y$-on át vezetne $Z$-re). Tehát a 3. axióma is teljesül.

 

III. Tekintsük hát pontoknak a végtelen sakktábla mezőit, távolságnak ama lóugrások számát, melynél kevesebb nem vezet kijelölt mezőről kijelölt mezőre és nevezzük az így értelmezett geometriát ‐ a közönséges geometriától megkülönböztetendő ‐ >>mesterséges geometriá<<-nak. Némi ízelítőt adunk a felmerülő kérdésekből. Elegendő lesz annak a viszonylag egyszerű kérdésnek a tisztázása, hogy van-e a mesterséges geometriában egyenes, helyesebben (egyenesvonalú) pontsor ?
Ha már megvan a pont és távolság fogalma (mégpedig a távolságnak az egyenestől függetlenül értelmezett fogalma), akkor a két fogalom segítségével a pontsor már definiálható. Lássuk ezt először is a közönséges geometriában.
(a) ‐ A közönséges geometriában három pontról ‐ $X$, $Y$, $Z$-ről ‐ akkor és csak akkor mondjuk, hogy lineáris ponthármas, ha az

$\begin{array}{c}{\displaystyle XY+YZ=XZ\mathrm{,}YZ+ZX=YZ\mathrm{,}ZX+XY=ZY}\end{array}$

távolság-relációk egyike teljesül.
Egynél több egyszerre nem is teljesülhet. Hiszen pl. ha az első kettő teljesülne, akkor ezekből az 1. és 2. axiómák alapján az $Y$ és $Z$ azonossága következnék. Tehát nem volna az $X$, $Y$, $Z$ (valódi) ponthármas, hanem csak pontpár.
(b) ‐ A közönséges geometriában akkor, de csak akkor mondjuk, hogy $Y$ az $X$ és $Z$ között van, ha az $XY+YZ=XZ$ távolság-reláció fennáll.
(c) ‐ A közönséges geometriában akkor, de csak akkor nevezzünk egy ponthalmazt (egyenesvonalú) pontsornak, ha bármely három pontja lineáris ponthármast alkot; de nincs a térnek a halmazhoz nem tartozó olyan pontja, mely a halmaz bármelyik két pontjával együtt lineáris ponthármast alkot.
A pontosvesszőig írt követelménynek pl. egy egyenes egyenlőközű pontsorozata is megfelel, mert e ponthalmaz bármely 3 eleme lineáris ponthalmazt alkot. A definíció második részének azonban már nem felel meg, mert található a halmazhoz nem tartozó pont ‐ mégpedig az euklideszi értelemben vett sorozóegyenes bármely pontja ‐ amely a halmaz bármely két pontjával együtt lineáris ponthármast képzett. Mondhatnók, hogy a szóbanforgó halmaz kibővíthető további elemmel úgy, hogy a bővített halmaznak is megvan az (a)-ban kikötött tulajdonsága. Tehát e két követelmény csak együtt képes az egyenes összes pontjait jellemezni.
Ha van olyan ponthalmaz a mesterséges geometriában, mely a (c) kirovásait teljesíti, akkor azt a mesterséges geometriában is egyenesvonalú pontsornak, röviden pontsornak nevezzük.
(a*) Tekintsük a 4. ábra $XYZ$, $ABC$ ill. $ABD$ ponthármasait.

 

 

4. ábra

 

Mindhárom lineáris ($1+2=3$, a két utóbbinál pedig $2+2=4$). Figyeljük meg: az első kettő egy euklideszi értelemben vett sorozóegyenesen helyezkedik el, míg $ABD$ euklideszi értelemben háromszöget alkot. Viszont az $UVW$ nem lineáris, hanem háromszög elrendezésű, sőt szabályos, abban az értelemben, hogy

$\begin{array}{c}{\displaystyle \varrho \left(UV\right)=\varrho \left(VW\right)=\varrho \left(WU\right)=\mathrm{2,}}\end{array}$

röviden:

$\begin{array}{c}{\displaystyle UV=VW=WU=2.}\end{array}$

(b*) Az $Y$ pont $X$ és $Z$ között, a $B$ pont az $A$ és $C$, ill. $A$ és $D$ között van.
(c*) A sakktábla valamely $X$ mezejéből kiinduló, egymás után tett, mindig $u_1$ irányú lóugrásokkal elért mezőket rendre jelölje: $X_1\mathrm{,}{X}_2\mathrm{,}{X}_3\mathrm{,}\text{...}$; az $u_5$ irányú lóugrással elért mezőket pedig jelölje rendre $X_{-1}\mathrm{,}{X}_{-2}\mathrm{,}{X}_{-3}\mathrm{,}\text{...}$. Az így létesített >>ponthalmaz<<

$\begin{array}{c}{\displaystyle \text{...}\mathrm{,}{X}_{-2}\mathrm{,}{X}_{-1}\mathrm{,}{X}_0\mathrm{,}{X}_1\mathrm{,}{X}_2\mathrm{,}\text{...}}\end{array}$

végtelen sok pontból áll és bármelyik három eleme lineáris hármast alkot, ami az

$\begin{array}{c}{\displaystyle X_m{X}_n=|n-m|}\end{array}$

távolság kifejezésből ‐ ahol $||$ a bennefoglalt kifejezés abszolút értéket jelenti ‐ könnyen belátható.
Azt is tudjuk bizonyítani (de hosszadalmassága, körülményessége miatt csak a IV. pontban fogjuk a bizonyítást sorra venni), hogy ha a most definiált

$\begin{array}{c}{\displaystyle \text{...}\mathrm{,}{X}_{-2}\mathrm{,}{X}_{-1}\mathrm{,}{X}_0\mathrm{,}{X}_1\mathrm{,}{X}_2\mathrm{,}\text{...}\text{<span style="font-style: italic;">(e)</span>}}\end{array}$

ponthalmazhoz bármely, hozzá nem tartozó $Y$ pontot csatolunk, akkor az így kibővített halmazra nézve már nem teljesül a >>bármely három pontja lineáris ponthármast alkot<< követelmény. Vagyis a bővített halmaz már nem képez pontsort. Eszerint a szóbanforgó (e) halmaz éppen egy egyenesvonalú pontsor.
Az $X_0$ mezőből kiindulva nemcsak az $u_1$, $u_5$ iránypárral folytatott lóugrás-sorozattal, hanem az $u_2\mathrm{,}{u}_6$; $u_3\mathrm{,}{u}_7$; $u_4\mathrm{,}{u}_8$ iránypárokkal is létesíthetünk pontsorokat. Így minden ponton (mezőn) >>átmegy<< négy olyan pontsor, amilyent az előbbiekben értelmeztünk.
Tüstént felmerül a kérdés, hogy kimerítettük-e a >>mesterséges tér<< összes pontsorait, vagyis az, hogy létezik-e a mondottakon kívül más ponthalmaz is, mely megfelel a (c)-ben adott két követelménynek ? Ennek és sok más, önmagától felmerülő kérdésnek a tisztázását azonban már az olvasóra bízzuk.

 

IV. A sakktáblára írt konfigurációk áttekinthetőbbek, ha a mezőket a mezők középpontjaival képviseltetjük, mint pl. az 1. ábrán. Ha e pontok sötét és világos jellegét nem tekintjük, akkor a végtelen sakktáblát képviselő ponthalmazt négyzetrácsnak, röviden rácsnak nevezzük. Rácsot alkotnak a derékszögű koordinátarendszerben ama pontok, amelyeknek koordinátái egész számok. Ha ennek a rácsnak a pontjait két osztályra bontjuk, egyikbe sorolva mindazokat, amelyeknek mindkét koordinátájuk vagy páros, vagy páratlan, a másik osztályba pedig a többit és a két osztály egyikét sötétre, másikat világosra színezzük, akkor előáll a sakktábla képviselője.
A pontrácson az egy mezőről kiinduló lóugrásokat egy rácspont nyolc különböző irányú eltolása képviseli (vö. 1. és 3. ábrát). Ha egy rácsponton átmenő egyenes iránytangense $1/2$, akkor az egyenes végtelen sok rácspontot fűz fel (mint az 5. ábrán pl. az $u$ egyenes). A felfűzött pontok egyenlőközű sorozatot képeznek az egyenesen, mégpedig ‐ ha a pontrács sakktábla-színezése, akkor ‐ váltakozó színű pontok sorozatát.
Ha mindazokat az egyeneseket megrajzoljuk, amelyek rácsponton mennek át és iránytangensük $1/2$, akkor csupa ilyen egyenlőközű pontsorozatra bontottuk a rácsot. Maguk az egyenesek pedig egyenlőközű sávokra bontják a síkot.
No most nézzük az 5. ábrát és hasonlítsuk össze a 2. és 3. ábrával.

 

 

5. ábra

 

Az 5. ábra sötét pontjainak nyolcszögű koszorúja olyan mint a 3. ábra két szélső övében foglalt sötét mezők váza. (Még néhány más, lényeges rácspont ki van emelve, de a többi rácspontot nem is jelöltük.) Most már sorra vesszük a III. (c*)-ban ígért bizonyítást és ahhoz az 5. ábrát tekintjük.
A sötét origóból kiindulva az $m=2n\left(>5\right)$ lóugrással elérhető pontok legyenek a nyolcszögű pontkoszorú (sötét) pontjai. (A 2. és 3. ábrával összefüggésben bizonyítottuk, hogy ezek a középső, sötét mezőt körülvevő $m$-ik és $\left(m-1\right)$-ik öv sötét mezőinek felelnek meg.)
Az origón átmenő, $1/2$ iránytangensű egyenes, az $u$ éppen a nyolcszögű pontkoszorú két szemközti, sötét pontját köti össze, az $X$ és $Y$ pontot. Ezt az $XY$ átlót a közbeeső rácspontok $2m=4n$ (lóugrásnak megfelelő) egyenlő szakaszokra bontják. Nyilvánvaló, hogy a rácspontokon átmenő, az $u$-val párhuzamos egyenesek ama szakasza, mely a sötét pontkoszorúból általuk felfűzött két legszélső pont ‐ $X_k$ és $Y_k$ ‐ közé esik, kisebb az $XY$ szakasznál. Vagyis mesterséges geometriánkban tekintve a távolságokat:

$\begin{array}{c}{\displaystyle XY=4n\mathrm{,}{X}_k{Y}_k<4n\mathrm{,}O{X}_k=2n\mathrm{,}O{Y}_k=2n\mathrm{,}\text{<span style="font-style: italic;">(g)</span>}}\end{array}$

mert $X_k$, $Y_k$ a $\left(2n\right)$-ik és $\left(2n-1\right)$-ik öv sötét, vagyis $2n$-essel számozott pontjai közül való pontok. Eszerint azonban mesterséges geometriánkban sem alkot lineáris hármast az $O{X}_k{Y}_k$.
Tekintsük most a III. (c*)-ban definiált $\text{...}\mathrm{,}{X}_{-2}\mathrm{,}{X}_{-1}\mathrm{,}{X}_0\mathrm{,}{X}_1\mathrm{,}{X}_2\mathrm{,}\text{...}$ ponthalmazt. Ez olyan, hogy a rácson éppen $1/2$ iránytangensű egyenesre, $u\text{'}$-re van mindegyik pontja felfűzve. Legyen továbbá egy $O$ rácspont a szóbanforgó ponthalmaz elemei közé nem tartozó. Ámde akkor a szó közönséges geometriai értelmében sincs rajta az $O$ az $u\text{'}$ egyenesen. Van-e olyan, az $O$ szerepét betöltő rácspont, amelyik az $u\text{'}$ rácspontjainak bármelyik kettejével együtt lineáris hármast alkot ‐ most a szó mesterséges geometriai értelmében ‐ ez itt a kérdés.
Színezzük úgy, sakktáblaszerűen a rácsot, hogy a tetszőlegesen kiválasztott $O$ rácspont sötét legyen. Ha $n$ egész számot elég nagynak választjuk, akkor az $O$ középhez tartozó $\left(2n\right)$-ik és $\left(2n-1\right)$-ik öv sötét rácspontjai alkotta koszorúnak és legalább két pontja az $u\text{'}$ egyenes $O$-val ellenkező oldalán. No de akkor lesz legalább kettő magán az $u\text{'}$ egyenesen is, amelyekkel pedig az $O$ ‐ a fennálló (g) relációk szerint ‐ nem alkothat lineáris hármast a mesterséges geometria értelmében sem. Eszerint hát az $u\text{'}$ egyenes rácspontjaihoz újabb rácspontot nem csatolhatunk, mert a bővített halmazban már $O$-hoz mindig van $u\text{'}$-nek két az $O$-val nem lineáris hármast alkotó pontja. Ezzel az ígért bizonyítást be is fejeztük.