Kezdőlap


Cím:	Képek a magyar matematika múltjából 4. Arany Dániel (1863-1944)
Szerző(k):	Obláth Richárd
Füzet:	1954/november, 65 - 71. oldal	PDF \| MathML
Témakör(ök):	Egyéb írások

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Lapunk címlapján olvasva nevét bizonyára több ifjú olvasónk feltette magában a kérdést, ki volt Arany Dániel. Ezekben a sorokban bemutatjuk őt.
Arany Dániel, mint a győri állami főreáliskola lelkes fiatal tanára 1894-ben megalapította a Középiskolai Mathematikai Lapokat. E tevékenységével nagy mértékben hozzájárult a magyar matematika mai virágzásához és világszerte tapasztalt megbecsüléséhez. A magyar ifjúság soraiban gyakori a tehetség. Nagy szolgálatot tesz tehát nemcsak a tehetséges ifjúnak, hanem a közösségnek is, aki elősegíti a tehetség kibontakozását, öntudatra ébredését és a neki megfelelő helyes irányba való terelését. A középiskolai matematikai folyóiratok ezt nem csökkenő eredménnyel és sikerrel teszik immár 60 év óta. Pedig ez az éremnek csak egyik oldala, hiszen a múltban sem, ma sem válik e lapok minden olvasójából ‐ mondhatom munkatársából ‐ matematikus, de abban nagy részük van, hogy ránevelik ifjúságunkat ‐ bármi lesz későbbi életpályájuk a problémák elemzésére, a szellemi munka örömeire. Minden olvasónk ismeri azt a nagy élvezetet, amit a feladatokkal való foglalkozás szerez és a nagy elégtételt, amit az akadályok leküzdésekor, a nehéz feladatmegoldása után érez. Így gyönyörűséggé válik ifjúságunk legjobbjai részére a komoly elmélyedést igénylő szellemi munka, az alkotás.
Mindez Arany Dániel érdeme, aki 60 évvel ezelőtt, amidőn a Műegyetemen kívül alig volt az országban matematikus, amidőn a középiskolai matematika tanítás eredménye szánalmas volt, matematikai lapot mert alapítani a középiskolai ifjúság részére és ezzel az alig parázsló tüzet lángra lobbantotta. Arany Dániel érdeme annál nagyobb, mert példa gyanánt is mindössze egy francia lap állt a szerény jövedelmű tanár előtt, amikor a biztos ráfizetést ígérő vállalkozásába kezdett. A magyar Középiskolai Mathematikai Lapok ugyanis a világ legrégibb ilynemű lapjai közé tartozik. Mintául csak a francia Journal de Mathématiques Elémentaires szolgálhatott. Fel is figyelt az új alapításra a nemzetközi szaksajtó; a német tanárok lapja pl. bő jelentésben számolt be az új lapról, de a középiskolai ifjúságnak szánt matematikai lapok a legtöbb országban még igen sokáig várattak magukra, pl. német nyelven csak kb. 5 év óta jelenik meg az a >>Archimedes<<. Nem a jelen cikk feladata a Középiskolai Mathematikai Lapok további sorsának követése, erről már régebben beszámoltam. ¹
Arany Dániel élettörténetét néhány szóval összefoglalhatom. A győri főreáliskolától csakhamar Budapestre került, ahol az első Tanácsköztársaság bukásáig működött mint a felsőbb ipariskola (technológia) tanára. A proletárdiktatúra idején tanúsított magatartása miatt a reakciós kormány nyugdíjazta, majd 1944-ben, a német megszállás idején, lakásából kizavarták és feleségével együtt egy kis szobában húzódott meg. Az ostrom alatt a nyilasok őt is, feleségét is meggyilkolták.
Arany Dániel alkotó matematikus is volt. Ifjú olvasóink már bizonyára hallottak a determinánsokról, amelyek az elsőfokú egyenletrendszerek általános megoldási képletében fellépő, elég bonyolult kifejezések. Sikerült azonban kitűnően kezelhető, áttekinthető jelölési módot találni, amely nagyon kényelmessé teszi használatukat. Ezáltal azután a matematika legkülönbözőbb részeiben igen jól használható segédeszközzé váltak a determinánsok. Ma már nemcsak a matematikában, hanem az alkalmazásokban is, különösen a fizikában nélkülözhetetlenek. A magyar matematika kezdő korszakában, főleg a múlt század hetvenes-nyolcvanas éveiben, a legrégibb nemzetközileg elismert magyar matematikus, Hunyady Jenő, a Műegyetem kiváló tanárának, hatása alatt a magyar matematika főjellemzője a determinánsok virtuóz kezelése volt. Ebbe az iskolába az ifjú Arany Dániel is beletartozott; a determinánselmélet figyelemreméltó eredményeket köszönhet neki.
Arany Dániel mindvégig megőrizte szellemi frissességét. Erre jellemző, hogy az analitikus geometriának egy új ‐ Morley (ejtsd: morli) angol matematikustól származó ‐ módszerét 77 éves korában sajátította el. Az iskolában megtanultátok a Descartes-féle két koordináta tengely használatát. A múlt század elején Feuerbach (akinek nevét sok olvasónk ismeri) és Möbius kiváló német matematikusok a két koordinátatengelyt háromszöggel pótolták. Ebben a rendszerben a pont helyzetét pl. a háromszög három oldalától való távolsága határozza meg ‐ ezek persze nem függetlenek egymástól. A háromszögre vonatkozó vizsgálatok egy részében ezek a koordináták célszerűbbek a Descartes-féléknél. Óriási irodalmuk van, új eredmények találása a segítségükkel éppen ezért egyre nehezebb, de a Morley-től a múlt század végén bevezetett ú.n. >>izotrop<< koordináták segítségével az utóbbi években is több kutató igen nagy eredményeket ért el a háromszög-geometriában. Itt a koordináta háromszög oldalai képzetesek, használatuk ezért lényegesen más, de Arany Dániel magas kora ellenére teljesen beleélte magát az új módszerbe.
Arany Dániel munkásságának nagy része a háromszög-geometriába tartozik, mégpedig elsősorban az ú.n. Simson (ejtsd: szimsz'n) egyenesre vonatkozik. Érvényes a következő tétel, melynek bizonyítását az olvasóra bízzuk (lásd a 639. sz. feladatot):
A háromszög köré írt kör kerületének bármely $P$ pontjából a háromszög oldalaira emelt merőlegesek talppontjai egy egyenesen vannak.
Ez tulajdonképpen Wallace (ejtsd: ualisz) tétele 1798-ból, de megrögzött, régi, téves adatok alapján ma is Simson-egyenesnek hívják a talppontokon átmenő egyenest.
A Simson-egyenesek sok hasznos sajátságuk folytán a háromszöggeometriában fontos szerepet játszanak. (Pl. felezik a $P$ pontot a magassági ponttal összekötő távolságot, ez a felező pont rajta van a Feuerbach-körön: a $P_{1}$ és $P_{2}$ pontokhoz tartozó Simson-egyenesek hajlásszöge egyenlő a körülírt kör $\hat{P_{1} P_{2}}$ ívéhez tartozó kerületi szöggel; ennek speciális esete, hogy a háromszög köré írt körben diametrálisan szembenfekvő pontokhoz tartozó Simson-egyenesek merőlegesek egymásra és a Feuerbach-körön metszik egymást stb. stb. A tétel akkor is igaz, ha $P$ -ből az oldalakhoz húzott egyenesek nem merőlegesek az oldalakra, hanem mindhárman ugyanazon szög alatt hajolnak az oldalakhoz stb.) Ezek közül Arany Dánielt leginkább az a sajátság foglalkoztatta, hogy ha $P$ végigfut a háromszög köré írt körön, a Simson-egyenesek háromcsúcsú hipocikloist ² burkolnak, vagyis minden Simson-egyenes ennek a görbének érintője.
Ez a háromcsúcsú hipociklois kapcsolatba került a már említett Morley egy nevezetes tételével. Ez a tétel a háromszög szögharmadolóiról szól és megállapítja, hogy a háromszög egy-egy oldalát közrefogó szögharmadolók metszéspontjai egyenlőoldalú háromszöget alkotnak. Ezt Morley-féle háromszögnek nevezik. Van der Woude, a hollandi leydeni egyetem tanára, 1940-ben bebizonyította, hogy a fentemlített ú.n. Steiner-féle 3-csúcsú hipociklois csúcsérintői merőlegesek a Morley-féle háromszög oldalaira.
Ez a szép felfedezés nagy hatást gyakorolt az akkor már idős Arany Dánielre, aki ettől kezdve igen sokat foglalkozott a Steiner-hipociklois és a Morley-háromszög kapcsolatával; új bizonyítást talált Van der Woude tételére és a hipociklois csúcsérintőjéről egy további tételt fedezett fel, melyben szerephez jutott a háromszög ú.n. >>ötödik nevezetes pontja<< (az izogonális pont), amelyből a háromszög mindhárom oldala $120^{\circ}$ -os szög alatt látszik.
Arany Dániel bebizonyította, hogy a Steiner-féle hipociklois csúcsérintői (melyek a csúcspontokban kétszeresen érintenek és természetesen átmennek a szilárd kör $F$ középpontján) párhuzamosak az $I A$ , $I B$ és $I C$ egyenesekkel, ahol $I$ az izogonális pont és $A$ , $B$ , $C$ a háromszög csúcspontjai. ‐ (Lásd ábrát.

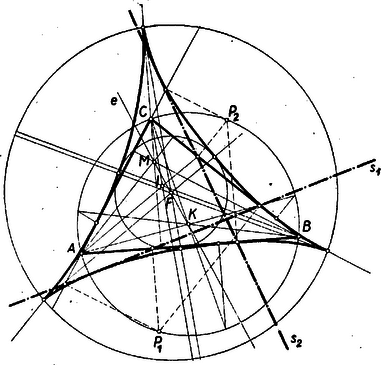
Ábránkon a háromszög köré írt

r

sugarú kör középpontját

K

-val, a talpponti háromszög köré írt, az ú.n. Feuerbach-féle kör középpontját

F

-fel, a magasságpontot

M

-mel jelöltük. Ismeretes, hogy

K

F

M

egy egyenesen, az

e

Euler-egyenesen vannak, és

K F = F M

. A

P_{1}

és

P_{2}

pontokhoz tartozó Simson-egyenesek:

s_{1}

ill.

s_{2}

érintik a Steiner-féle hipocikloist, amely görbe még érinti, mint speciális Simson-egyeneseket a háromszög oldalait és magasságvonalait, továbbá érinti az

\frac{r}{2}

sugarú Feuerbach-kört három ‐ egyenlőoldalú háromszöget alkotó ‐ pontban. A hipociklois szilárd köre koncentrikus a Feuerbach-körrel és sugara

\frac{3}{2} r

)
A középiskola anyagát meghaladó hosszadalmas számolásokon alapuló bizonyításait nem ismertethetem. Csak még egy személyes élményt mondok el, mely mutatja, hogy Arany Dániel mily lelkesedéssel és kitartással foglalkozott a háromszög-geometriával. Egy ízben meglátta nálam Gallatly (ejtsd: galetli) angol matematikus >>The modern Geometry of the triangle<< című nagyszerű könyvét. Nyomban kölcsönkérte tőlem. Egy idő múlva az egyik könyvkereskedésből hozták el hozzám a könyv egy új példányát >>Arany tanár úr megbízásából<<, akinek a könyv annyira megtetszett, hogy jóformán naponként olvasta és nem akart tőle többé megválni.
Érdeklődésének másik fő tárgya a valószínűségszámítás néhány érdekes kérdése. A valószínűségszámítás elemeit Lapunk nemrég ismertette, ³ ezekre tehát nem térek ki.
Arany Dániel a valószínűségszámítás két érdekes problémájával foglalkozott. Az egyik az ú.n. >>játéktartam<< problémája. Ez legegyszerűbb alakjában a következő: ketten

A

és

B

játszanak.

A

-nak

x

forintja van,

B

-nek

y

forintja. Minden játszma 1 forintba megy.

A

nyerési valószínűsége

p

B

-é

q = 1 - p

. Mi annak a valószínűsége, hogy

k

játszma után

A

minden pénzét elvesztette. Arany Dániel ennek a feladatnak különböző változataival foglalkozik. Kiterjeszti három játékos esetére, de ekkor a feladat annyira bonyolult, hogy megoldását csak egy numerikus példán mutatja be.
A másik valószínűségszámítási feladat, amelyre több munkájában visszatér, az ú.n. >>bolyongási<< probléma. Ez lényegében az első világháború óta külföldön élő Pólya György magyar matematikustól (jelenleg a californiai Stanford egyetem világhírű professzora) származik és hasznosnak bizonyult a modern fizikában és csillagászatban. Az Arany Dániel tárgyalta egyszerűbb esetben így hangzik: valaki bizonyos sebességgel elindul egy útvesztőben, ahol minden út-irány egyenlően jogosult. Mi a valószínűsége, hogy

t

idő múlva

k

távolságra lesz kiindulópontjától.
Arany Dániel ‐ részben Jordan Károlynak, a mai magyar matematikusok kiváló Nesztorának segítségével ‐ a valószínűségszámításnak, a fent említettekkel összefüggő, magasabb problémáival is foglalkozott. De ezeket nem lehet ily egyszerűen elmondani.
Be akarok azonban egész röviden számolni a valószínűségszámítás igen fontos gyakorlati alkalmazásai körébe tartozó munkásságáról. Nyugdíjas évei kezdetén ugyanis, mint biztosítási matematikus működött, és Magyar László fővárosi iskolaigazgatóval közösen könyvet írt az életbiztosítás matematikájáról. A biztosítási matematika terjedelmes tudományág, évekig tartó tanulmányozást igényel, de alapelvét igen röviden el lehet mondani.
Senki sem tudhatja, hogy akár önmaga, akár felebarátja meddig fog élni, de ha egy nagyobb embertömegre ‐ például egy ország lakosságára ‐ vonatkozólag tesszük fel a kérdést, hogy pl. a valamely időpontban élő

x

éves emberek közül hányan lesznek

k

év múlva még életben, arra a tudomány elég nagy pontossággal meg tud felelni. (Természetesen az emberi élettartam nem tekinthető pusztán véletlen jelenségnek. Kolmogorov híres szovjet tudós mondta, küldjetek a falura orvost és bábát és az élettartam nyomban meg fog hosszabbodni. Ugyanezt mondhatnók minden egészségügyi intézkedésre. Minél több új, egészséges lakást, kövezett utat, vízvezetéket stb. építünk; annál észrevehetőbben hosszabbodik meg az élettartam, vagy ellenkezőleg, egy esetleges háború következtében viszont nyomban megrövidülne.) A matematikai statisztikának módszerei vannak arra, hogy a tapasztalatokat táblázatba foglalja, amelyből az emberi élettartam valószínű alakulása elég nagy pontossággal kiolvasható. Az ilyen táblázatot halandósági táblázatnak nevezik, de a mondott okoknál fogva időnként felülvizsgálatra szorul. Pl. az 1930. évi magyar férfiak néphalandósági táblázata szerint 100 000 újszülött fiú közül

\begin{matrix} \begin{matrix} 15 & éves & korát & eléri & 76 536, \\ 30 & << & << & << & 70 821, \\ 50 & << & << & << & 60 583, \\ 75 & << & << & << & 24 231. \end{matrix} \end{matrix}

Ha tehát, amint általánosan szokás, az

x

éves élők számát

l_{x}

-szel jelöljük, annak valószínűsége, hogy egy újszülött fiú 50 éves korát megéri

\begin{matrix} \frac{l_{50}}{l_{0}} = \frac{60 583}{100 000} = 0, 60583. \end{matrix}

Az életbiztosítás feladata pl. az, hogy elhalálozás esetén a hátramaradottak bizonyos összeget kapjanak. Ezért a biztosítást keresőnek, a biztosítottnak, természetesen díjat kell fizetnie. A díjszámítás alapja az, hogy a biztosító vállalat várható bevételeinek és kiadásainak bármely pillanatban egyenlőeknek kell lenniök. Ezt az elvet és alkalmazását jobban megértjük, egyszersmind a biztosítási matematikába jobb betekintést nyerünk, ha hosszadalmas magyarázatok helyett egy részletesen kidolgozott egyszerű példán követjük.
Az olvasó emlékezetébe idézem a kamatos kamatszámítás alapformuláját, mely szerint a

T

tőke

n

időszak (pl. év) alatt felnövekedett

T_{n}

értékére, ha minden időszak végén az esedékes kamatot is a kamatozó tőkéhez csatolják (szakkifejezéssel, ha a tőkét kamatos kamataival számítják), a

\begin{matrix} T_{n} = T r^{n} \end{matrix}

összefüggés áll fenn: itt, ha 1 Ft-nak egy időszakra eső kamatát

i

-vel jelöljük,

\begin{matrix} r = 1 + i . \end{matrix}

Ha viszont azt kérdezzük, hogy mekkora

T

összeg az, amelyik a időszak alatt kamatos kamataival

T_{n}

értékére növekszik, akkor az előbbi képlet megfordításával a

\begin{matrix} T = T_{n} v^{n}, v = \frac{1}{1 + i} \end{matrix}

képlet adódik. Itt

v

-t diskonttényezőnek és

T

-t a

T_{n}

érték diszkontált értékének, vagy mai értékének nevezzük.
Feltesszük, hogy egy

x

éves egyén oly módon köt biztosítást, hogy, ha

n

éven belül meghal, hátramaradottainak azonnal kifizetendő 1 forint, ha

n

év múlva életben van, önmaga kapja az 1 forintot. Mekkora évi díjat kell ezért a biztosításért fizetnie ? (Ha a biztosítást nem 1 forintra, hanem

T

forintra kötik, a díj természetesen az 1 forint biztosítása díjának

T

-szerese.)
A számítások egyszerűsítése végett felteszik, hogy a halálozások az év végén, a születések az év elején történnek, ennek megfelelően a díj az év elején, míg a biztosított összeg kifizetése az év végén esedékes. Feltesszük továbbá, és ez az elv a számítás szempontjából igen fontos, hogy az összes

x

éves élők ugyanily biztosítást kötnek. Ezen megállapodások rögzítése után a díj kiszámítása már könnyű.
Az egyenlet felállításának elve, amint már hangsúlyoztuk, hogy a biztosítás megkötésekor is (mint bármikor) a várható kiadások értéke ugyanaz legyen, mint a várható díjbevétel értéke. Nem vehetjük azonban a különböző időkben esedékes kiadásokat és bevételeket az akkor kifizetendő, illetőleg befolyó értékükkel, hiszen minél később kerülnek kifizetésre, illetve minél hamarabb folynak be, annál többet érnek kamatos kamataikkal együtt. Így célszerű minden összeg helyett azt az értéket (diszkontált értéket) számítani, amely a biztosítás kötésétől kamatozva érné el az esedékes összeget az esedékesség napjára. Így az egyenlet felállításának elvét pontosabban így kell fogalmazni: a várható kiadások diszkontált értéke kell, hogy megegyezzék a várható díjbevételek diszkontált értékével.
Mik tehát a kiadások ? Az első év végén az év folyamán elhaltak mindegyike miatt ki kell fizetni

1 - 1

Ft-ot. Az

x

-edik évüket elérők számát

l_{x}

-szel jelöltük, ekkor az

x + 1

-edik év folyamán elhalálozók

d_{x}

számára

\begin{matrix} d_{x} = l_{x} - l_{x + 1}, \end{matrix}

tehát a kifizetendő összeg

d_{x}

forint, de a megállapodás szerint ezt csak az év végén fizetjük, tehát mai értéke

d_{x} v

; a második év végén a második évben elhaltak után kell

l_{x - 1} - l_{x - 2} = d_{x + 1}

Ft-ot fizetni, minthogy ezt csak a második év végén fizetjük, a kifizetés értéke a biztosítás megkötésekor

d_{x + 1} v^{2}

; a harmadik évben elhaltak után kifizetendő összeg értéke a biztosítás megkötésekor

d_{x + 2} v^{3}

és így tovább, az utolsó, az

n

-edik évben

d_{x + n - 1}

halott után kifizetendő összeg értéke a biztosítás megkötésekor

d_{x + n - 1} v^{n}

. Kifizetendő továbbá a biztosított összeg az összes

n

év múlva még életben lévő személyeknek, számuk

1_{x + n}

, az összeg diszkontált értéke

1_{x + n} v^{n}

. Az összes kiadások értéke tehát

\begin{matrix} d_{x} v + d_{x + 1} v^{2} + \dots + d_{x + n - 1} v^{n} + l_{x + n} v^{n} . \end{matrix}

Mik a bevételek ? A most használt okoskodások alkalmával azonnal látjuk, hogy a mindenkor élők részéről fizetett díjak diszkontált értéke (tehát ha az évi díjat

P

-vel jelöljük):

\begin{matrix} P (l_{x} + l_{x + 1} v + ... + l_{x + n - 1} v^{n - 1}) . \end{matrix}

Ugyanis az első évben a díjat

l_{x}

számú élő fizeti, s minthogy a díj az év elején fizetendő, az első évben diszkontálni nem kell. A

k

-ik évben fizetendő díjat az év elején élő

l_{x + k - 1}

élő fizeti és ez

k - 1

évre diszkontálandó. Az egyenlet tehát, amelyből a díj kiszámítható

\begin{matrix} P (l_{x} + l_{x - 1} v + ... + l_{x + n - 1} v^{n - 1}) = d_{x} v + d_{x + 1} v^{2} + ... + d_{x + n - 1} v^{n} + l_{x + n} v^{n} . \end{matrix}

Amint látható, ez az egyenlet hosszabb ‐ 20‐30 éves ‐ tartamú biztosításnál elég kényelmetlen számításokra vezetne, de nem azért értünk a matematikához, hogy ilyen nehézségeken ne lehessünk úrrá. Diszkontáljuk mindkét oldalt a születésre, vagyis szorozzuk mindkét oldalt

v^{x}

-szel, ami az egyenlet helyességét nem befolyásolja. Az egyenlet most így szól

\begin{matrix} P (l_{x} v^{x} + l_{x + 1} v^{x + 1} + ... + l_{x + n - 1} v^{x + n - 1}) = \\ = d_{x} v^{x + 1} + d_{x + 1} v^{x + 2} + ... + d_{x + n - 1} v^{x + n} + l_{x + n} v^{x + n} . \end{matrix}

A két oldalon szereplő összegek helyett az egész táblázat végéig terjedő összegeket célszerű használni, mert ezek már csak az

x

kezdő indextől függenek, a biztosítás időtartamától nem. Bevezetve a

\begin{matrix} D_{x} = l_{x} v^{x}, & C_{x} = d_{x} v^{x + 1}, \\ N_{x} = D_{x} + D_{x + 1} + \dots, & M_{x} = C_{x} + C_{x + 1} + ... \end{matrix}

jelöléseket, ahol az összegezés a táblázat végéig történik; eredményünk így alakul:

\begin{matrix} P (N_{x} - N_{x + n}) = M_{x} - M_{x + n} + D_{x + n}, \end{matrix}

és innen a keresett évi díj

\begin{matrix} P = \frac{M_{x} - M_{x + n} + D_{x + n}}{N_{x} - N_{x + n}} . \end{matrix}

N_{x}

és

M_{x}

ú.n. alapszámokat táblázatokba szokás foglalni, a díj tehát innen már kényelmesen kiszámítható.
A számítás elve, hogy a várható bevételeknek egyenlőknek kell lenniük a várható kiadásokkal, nem nyújt fedezetet a biztosító vállalat költségeire és fennálló kockázatára, ezért az így kiszámított díjhoz, az ú.n. >>nettodíj<<-hoz a biztosító társulat néhány százalék pótlékot ad hozzá, és ez a felek által tényleg fizetendő díj.
Nem szándékunk a biztosítási matematika tömérdek egyéb, jóval komplikáltabb problémájának bemutatása, ezen a nagyon egyszerű feladatara is láthattuk a valószínűségszámítás alkalmazását a gyakorlatban, egyszersmind összefüggést találtunk Arany Dániel munkásságának különböző tárgykörei között.
Arany Dánielben volt valami kedves közvetlenség; ha valamely matematikai folyóiratban őt érdeklő cikket talált, rögtön írt a cikk szerzőjének ‐ amiben nyelvismerete is segítségére volt, jól tudott németül, franciául, angolul ‐ és általában eltalálta a megfelelő hangot, úgy hogy igen élénk összeköttetésben volt az egész világ szakköreivel. A civilizált világ majdnem minden, a háromszög-geometria művelésével foglalkozó szaklapjában jelentek meg, néha csak pár soros közleményei; késő öregkorában is örült minden egyes megjelenő cikkének. Munkakörébe vágó érdekes szakkönyvtárt gyűjtött; amidőn 1944-ben a fasiszta intézkedések miatt szűkebb lakásba kellett költözködnie, könyvtárát az Eötvös Loránd Matematikai és Fizikai Társulatnak ajándékozta és Hajós György professzor buzgalmának sikerült a könyvtár megmentése, mely ma a műszaki egyetem 1. számú matematikai tanszékének birtokában van, külön kezelésben.
Áttekintettük Arany Dániel matematikai munkásságát, de itt Davyre (ejtsd: dévi) a híres angol fizikusra kell gondolnom. Davyt megkérdezték, melyik felfedezésére a legbüszkébb, azt felelte Faradayre (ejtsd: feredé). Arany Dániel matematikai eredményeinek ellenére legnagyobb érdemének a középiskolai lapok megalapítását kell tekintenünk, amely cselekedetével sokakat nyert meg a matematikának és ezzel hazájának is, a tudománynak is kimagasló szolgálatot tett !

¹Obláth R.: >>A Középiskolai Matematikai Lapok és a matematikai versenyek múltjáról<<. Középiskolai Matematikai Lapok. Új sorozat II. kötet, 1949, 3‐7. old.

²Ha valamely szilárd kör kerületén, a kör belsejében gördül egy olyan kör, amelynek átmérője a szilárd kör átmérőjének $n$ -ed része $(n \geq 3)$ , akkor a gördülő kör bármely pontja $n$ -csúcsú hipocikloist ír le ( $n = 2$ esetén a görbe egyenessé fajul.)

³Prékopa András: >>A valószínűségszámítás elemei<< VI. kötet 2. és 4. szám (1953. febr. ill. ápr.)