Cím: Az 1954. évi Rákosi Mátyás matematikai tanulmányi verseny I. fordulója
Füzet: 1954/május, 129 - 136. oldal  PDF  |  MathML 
Témakör(ök): OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ezidén e verseny március 9-én ugyanolyan szabályok szerint folyt le az egyes iskoláknál, mint tavaly: csak a gimnáziumok és ipari technikumok III. és IV. osztályú tanulói indulhattak. Munkaidő: 5 óra. Az elrendelt házi, selejtező versenyek ellenére a résztvevők száma most is 3000-en felül volt és a beadott 2896 dolgozat (209 iskolából) sem maradt el lényegesen a tavalyi 2943 mögött, csakhogy az idén az ipari technikumok 757 beadott dolgozattal szerepeltek a tavalyi 353 helyett. A versenybizottság határozata alapján az április 20-iki döntőbe 287 tanuló került (a beadott dolgozatok 9,8%-a) a tavalyi 189 (6,4%) tanulóval szemben. Az ipari technikumi tanulók közül, a tavalyi 24-gyel szemben, ez idén 41-en kerültek a döntőbe, ami számszerűen mégiscsak gyarapodás, ha százalékos arányban csökkenést is jelent. (Inkább arra mutat, hogy túl sok ipari technikumi tanuló indult.) A részletes adatok a mellékelten közölt megyék és iskolafajok szerinti kimutatásban megtalálhatók.
Mikor örömmel állapítjuk meg, hogy a döntőbe jutott 287 tanuló közül 128-an (44,6%) lapunk feladatmegoldói, egyben rá kell mutatnunk, hogy milyen nagy számmal vannak még tanulók, sőt egész iskolák, amelyek még nem kapcsolódtak be a Középiskolai Matematikai Lapok munkájába. Érdekes még megemlíteni, hogy a tavalyi Arany Dániel versenyen helyezést elért 45 II. oszt. tanuló és a Rákosi versenyen helyezett 29 III. oszt. tanuló közül, 13, ill. 4 kivételével, ez idén is mind bejutottak a döntőbe.
Alább közöljük a kitűzött három feladatot a megoldásokkal együtt:

 

1. feladat. Bizonyítandó, hogy ha a és b pozitív számok, akkor
(a+b)(a4+b4)≥(a2+b2)(a3+b3)

Megoldás: Elegendő megmutatni, hogy a két oldal különbsége nem lehet negatív. Alakítsuk át e különbséget:
(a+b)(a4+b4)-(a2+b2)(a3+b3)=a4b-a3b2-a2b3+ab4==ab[a2(a-b)+b2(b-a)]=ab(a-b)(a2-b2)=ab(a+b)(a-b)2


Ez akkor nem negatív, ha ab(a+b) nem negatív, ami pedig teljesül, ha sem a sem b nem negatív, továbbá akkor is, ha a és b különböző előjelűek, mégpedig közülük a nagyobb abszolút értékű negatív.
 

Megjegyzés: Azáltal, hogy ab, ill. a+b-vel nem osztottunk, módunk nyílt a feladat követelményein túlmenő megállapításokat tenni. Természetes, ha csak a feladat állítását akarjuk bizonyítani, akkor lehet ab és a+b-vel osztani, de akkor nem elég rámutatni, hogy az osztó ≠0-val, hanem az osztó előjele is lényeges; továbbá meg kell vizsgálni mindenkor, hogy egyenértékű átalakításokat végeztünk-e, vagy pedig megmutatni, hogy a nyert helyes eredményből visszafelé következtetve egyértelműen jutunk a kiinduláshoz. (Lásd a beszámoló zárómegjegyzéseit is.)
Kimutatás az 1954. évi Rákosi Mátyás matematikai verseny I. fordulájáról megyék és iskolafajok szerint

B e a d o t t   d o l g o z a t o kD ö n t ő b e   k e r ü l t      Megyék ésGimnáziumIp. tech-ÖsszesenGimná-Ip. tech-Összesennikumziumnikum       Budapest  i0t00i t0i0t0i t00i t0i0t0s0a00s a0s0a0s a00s a0s0a0k0n00k n0k0n0k n00k n0k0n0o0u00o u0o0u0o u00o u0o0u0l0l00l l0l0l0l l00l l0l0l0a0ó00a ó0a0ó0a ó00a ó0a0ó0 1. Baranya4  953  617  1562  43  35  7 2. Bács-Kiskún19  871  910  965  81  26  10 3. Békés10  1331  1511  148  ‐  ‐1  21  2 4. Borsod7  765  7812  1546  83  39  11 5. Csongrád7  823  5510  1372  22  44  6 6. Fejér2  293  355  642  41  13  5 7. Győr‐Sopron9  684  5913  1276  23  ‐  ‐6  23 8. Hajdú‐Bihar9  1093  4612  1555  162  27  18 9. Heves3  551  34  582  71  13  810. Komárom8  783  1711  954  5  ‐  ‐4  511. Nógrád2  241  43  282  71  13  812. Pest7  251  18  263  41  14  513. Somogy4  521  225  742  3  ‐  ‐2  314. Szabolcs‐Szatmár5  562  317  87  ‐  ‐  ‐  ‐  ‐  ‐15. Szolnok11  1191  1312  1326  11  ‐  ‐6  1116. Tolna5  86  ‐  ‐5  864  7  ‐  ‐4  717. Vas7  109  ‐  ‐7  1095  7  ‐  ‐5  718. Veszprém6  982  528  1504  92  26  1119. Zala2  32  ‐  ‐2  322  2  ‐  ‐2  2Vidék117  141335  501152  191462  12718  2280  14920. Budapest40  72617  25657  98232  11911  1943  138  Összesen157  213952  757209  289694  24629  41123  287

1
 

2. feladat. Adva van egy háromszög és három párhuzamos egyenes. Szerkesszünk olyan háromszöget, amely az adott háromszöghöz hasonló és csúcsai az adott egyeneseken vannak.
 

I. megoldás. Készítsünk vázlatot, a középső párhuzamos távolság a másik kettőtől legyen p és q, a középső egyenes messe BC-t a D pontban (a jelöléseket az 1. ábra mutatja). Ekkor nyilván BD:DC=p:q.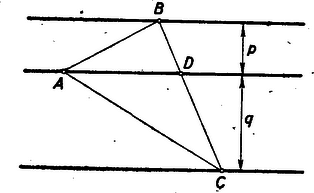
 
 
1. ábra
 

Ennek alapján a szerkesztés menete: az adott A'B'C' háromszögben megszerkesztjük a B'C'-t p:q arányban osztó D' pontot (2. ábra).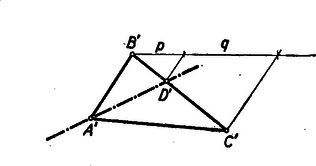
 
 
2. ábra
 

B'-ben és C'-ben párhuzamost húzunk A'D'-vel, már a keresett ábrához hasonlót kapunk. Ezt kell szükség szerint nyújtani, vagy zsugorítani az adott egyeneseknek megfelelően.
Ez például úgy tehető meg, hogy a középső párhuzamos egyenesre rámásoljuk az A'D' távolságot és e fölé mint közös oldal fölé, átmásoljuk a 2. ábrából a p, ill q szélességű síksáv oldalaira az A'D'B', ill. A'D'C' háromszögeket. Így egy az eredetileg megadott háromszöggel egybevágó A'B'C'▵-et nyerünk (3. ábra).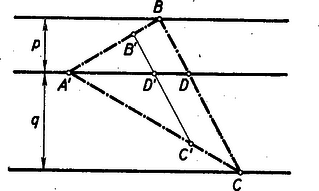
 
 
3. ábra
 

Messe az A'B' oldal a p szélességű síksáv külső szélét B-ben, és húzzunk B-n át B'C'-vel párhuzamost, amely az A'D'-t D-ben, az A'C'-t C-ben metszi. Az így nyert ABC▵ az A'B'C'▵-nek az A' pontból ABA'B' arányban való nagyítása (ill. kicsinyítése) és BDDC=B'D'D'C'=pq miatt a C pont szükségképpen a q szélességű síksáv külső szélén fekszik. Tehát az ABC▵ eleget tesz követelményeinknek.
Tetszés szerint választhatjuk ki, hogy melyik csúcs megfelelője melyik egyenesre essék, tehát 3!=6-féle megoldás lehetséges. Az ezekből tükrözéssel és eltolással keletkező megoldások már mind egybevágóak e 6 háromszög valamelyikével s így nem adnak azoktól lényegesen különböző megoldást.
 

II. megoldás. A B pontot úgy vihetjük át C-be, hogy elforgatjuk A körül a BAC∢=B'A'C'∢= szöggel és közben ACBC=A'C'A'B'=b'c' arányban meg is nyújtjuk, (vagy rövidítjük, A'B'C' legyen az adott háromszög). Mivel e mozgások adatai függetlenek a keresett megoldástól, a feladatot megoldhatjuk forgatva nyújtással.
Válasszunk pl. a középső egyenesen tetszőlegesen egy A pontot és e körül forgassuk el a felső egyenest B'A'C'=α szöggel és egyidejűleg nyújtsuk A-ból A'C':A'B'=b':c' arányban (4. ábra).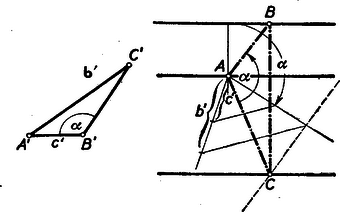
 
 
4. ábra
 

A kapott egyenes messe az alsó párhuzamost C-ben és szerkesszük meg a felső egyenes azon B pontját, mely a forgatva nyújtásnál C-be ment át. Az ABC▵ A-nál lévő szöge és az ezt közrezáró oldalak aránya megegyezik az A'B'C' háromszög megfelelő adataival, tehát valóban hasonló a két háromszög.
 

III. megoldás: Készítsünk vázlatot. Rajzoljuk meg a háromszög köré írt kört, messe ez a középső párhuzamost A-n kívűl még a D pontban. Ekkor a kerületi szögek tétele szerint
ADB∢=ACB∢ésADC∢=ABC∢.
Ennek alapján a szerkesztés, ha az adott háromszög A'B'C': a középső egyenes tetszés szerinti D pontjában rámérjük ezen egyenes egyik félegyenesének két oldalára az A'C'B', ill. A'B'C' szögeket (5. ábra).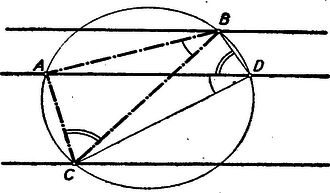
 
 
5. ábra
 

Messék ezek a megfelelő párhuzamos egyenest B-ben, ill. C-ben. Mérjük rá végül BC-re C-ben a B'C'A'∢-et BC ellenkező oldalára mint amelyiken D van. Messe ez a középső párhuzamost A-ban. Az AB távolsága C és D pontokból egyenlő szög alatt látszik, s így ABCD húrnégyszög. Ebből következik, hogy ABC∢=ADC∢=A'B'C'∢, tehát az ABC▵ szögeiben megegyezik az adott A'B'C'▵-gel, s így hasonló hozzá.
 

3. feladat. Állítsunk merőlegest egy parabola érintőjére az érintési pontban, és ezt messük el a fókuszon átmenő, az érintővel párhuzamos egyenessel.
Mi a metszéspontok mértani helye, ha az érintési pont végigfut a parabolán?
 

I. megoldás. Válasszuk a parabola tengelyét x-tengelynek, csúcsérintőt y-tengelynek, ekkor a parabola egyenlete
y2=2px.
Legyen a parabola x1, y1 pontja az érintési pont, akkor az érintő egyenlete
yy1=p(x+x1),
ahol
y12=2px1,
azaz
x1=y122p.
Így az érintési pontban emelt merőleges, ill. az F(0,p2) fókuszból az érintővel párhuzamosan húzott egyenes egyenlete
y-y1=-y1p(x-y122p)
azaz
2py1x+2p2y=y1(y12+2p2)
illetve
y=py1(x-p2),
azaz
2px-2y1y=p2.
Innen kiküszöbölve y-t, ill. x-et
2p(y12+p2)x=y14+2p2y12+p4=(y12+p2)2;2(p2+y12)y=y1(y12+p2).
Oszthatunk p2+y12-tel, mert ez nem lehet 0 és y1-et kiküszöbölve kapjuk, hogy 2y=y1; 2px=y12+p2=4y2+p2, azaz y2=p2(x-p2); ez pedig olyan parabola egyenlete, melynek csúcspontja (01p2), az eredeti parabola fókusza, paramétere pedig az eredeti parabola paraméterének negyedrésze.
*

A feladat megoldható koordináták és (ami lényegében ugyanazt jelentené) Pythagoras tételének felhasználása nélkül is. Ekkor a következő összefüggésekre lesz szükségünk: a parabola tetszés szerinti P pontjának a vetülete a direktrixen legyen Q, ekkor a P pontban húzott érintő az FPQ∢ szögfelezője, vagy ami ezzel egyenértékű, a parabola fókuszából az érintőkre bocsátott merőlegesek talppontjainak mértani helye, a parabola csúcsérintője.
Valóban meghúzva az FPQ∢ felezőjét (mely merőlegesen metszi QF-et a csúcsérintőre eső R felezőpontban), erre FP=PQ, de az egyenes bármely más P' pontjára FP'=P'Q, az utóbbi távolság pedig nagyobb P'-nek a direktrixtől mért távolságánál (6. ábra).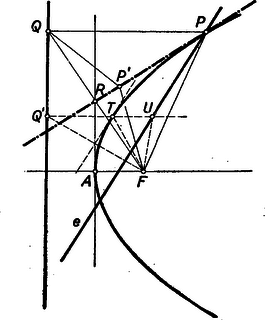
 
 
6. ábra
 

Így az egyenesnek minden P-től különböző pontja a direktrixhez közelebb van, mint a fókuszhoz, tehát a parabola ugyanazon oldalára esik. Könnyen látható az is, hogy minden más P-n átmenő egyenesnek van pontja a parabolának mindkét oldalán2. Így valóban e szögfelező a parabola érintője. Az ábra alapján fordítva is könnyű a csúcsérintő bármely R pontjához megkeresni azt a P pontot a parabolán, melyben húzott érintőre F-ből merőlegest bocsátva annak talppontja, éppen R lesz.
 

II. megoldás: Legyen P-ből a direktrixre bocsátott merőleges talppontja Q, FQ felezőpontja R, az érintőre P-ben bocsátott merőleges és az F-ből az érintővel húzott párhuzamos metszéspontja M (7. ábra).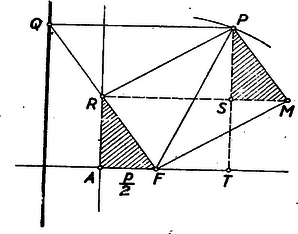
 
 
7. ábra
 

A segédtétel szerint FRP∢=90∘, tehát az FMPR négyszög téglalap, így MP♯FR, de akkor egyszersmind MR∥PQ. Bocsássunk P-ből merőlegest a parabola tengelyére; messe ez MR-t, ill. a tengelyt az S, ill. T pontban. Ekkor az oldalak párhuzamossága és MP=FR miatt, MPS▵≅FRA▵, s így PS=RA=12PT, MS=FA=p2.
Az M pontok mértani helye tehát az adott parabolából a következő módon keletkezik: először minden pontnak a parabola tengelyétől való távolságát felére csökkentjük, azután az így keletkezett görbét p2 távolsággal eltoljuk. Az utóbbi lépés a görbe alakját nem változtatja meg; az A pontot, mely az első lépésnél helyben marad, F-be viszi át. Az első lépésnél viszont a parabolából újabb parabola keletkezik, melynek a csúcsa és tengelye azonos az eredeti parabolával, paramétere pedig negyed-akkora. (L. jelen számunkban a 618. sz. feladatot.)
 

III. megoldás. Az FMPR téglalap átlói egyenlők és felezik egymást, így RN, mint az FPQ▵ középvonala párhuzamos QP-vel, vagyis merőleges a csúcsérintőre és RN=NF (8. ábra), tehát az N pont olyan parabolát ír le, melynek az eredeti parabolával közös a fókusza, direktrixe pedig az eredeti parabola csúcsérintője, tehát paramétere p2.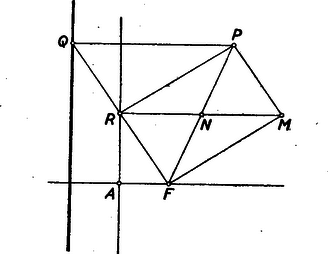3
 
 
8. ábra
 

Minden egyes N pontból úgy nyerjük a megfelelő M pontot, hogy a csúcsérintőtől való távolságát kétszeresre nyújtjuk. Ezzel ismét parabolát nyerünk, amelynek újra feleződik a paramétere, csúcsa pedig F-be kerül.
 

Megjegyzés: Felhasználtuk, hogy ha egy parabolát a direktrixtől egy irányban kétszeresen megnyújtunk, vagy ha ugyancsak egy irányban a tengelye felé 1/2 arányban összehúzzuk, akkor ismét parabolát kapunk, mindkét esetben kisebb paraméterrel: előbbi esetben az eredeti paraméter fele, utóbbi esetben a negyede lesz az új paraméter. Ez azonban semmikép sem magától értetődő, még csak az összes parabolák hasonlóságából sem következik. Legkönnyebb koordináták segítségével belátni. (Mellesleg az első megoldásban M koordinátáira adódó x=12p(y12+p2)=x1+p2, y=y12 is éppen a II. megoldásban elemien bizonyított összefüggéseket fejezi ki.) A II. és III. megoldásban viszont éppen a koordinátákat akartuk elkerülni, tehát csak akkor mondhatjuk, hogy ez sikerült, ha a föntebb említett tényeket is koordináták és Pythagoras tételének felhasználása nélkül tudjuk bizonyítani. Ez sem ütközik nehézségbe. A III. megoldásra vonatkozóan megmutatjuk, a II. megoldással kapcsolatos bizonyítást ennek alapján az olvasóra bízzuk (l. a 618. feladatot).
Legyen d, A és F egy parabola direktrixe, csúcsa és fókusza; P egy pontja, Q annak vetülete d-n és legyen QP'=2QP (9. ábra).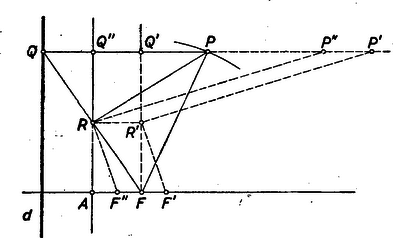
 
 
9. ábra
 

Segédtételünk értelmében QF szakasz R felezőpontjára PRF∢=90∘ és R természetesen a csúcsérintőn van. Ha P' valóban parabolát ír le, akkor ennek csúcsa az F pont kell, hogy legyen. Az ebben d-vel párhuzamosan húzott egyenes messe a PQ egyenest Q'-ben, felezőpontja legyen R'. Ismét segédtételünk értelmében elegendő azt megmutatni, hogy az R'-ben P'R'-re bocsátott merőleges egy a P' pont helyzetétől független F' pontban metszi az AF tengelyt.
Toljuk el R'P'-t önmagával párhuzamosan úgy, hogy R'R-be kerüljön. Ugyanez az eltolás vigye F'-t, P'-t, ill. Q'-t, F'', P'' Q''-be. Mivel F'F''=RR'=p2, független a P' pont helyzetétől, így elegendő azt megmutatni, hogy F'' helyzete is független. Tudjuk, hogy
QQ''=RR'=P''P',amibőlQ''P''=2Q''P.
Mivel
PRF∢=P''RF''∢=90∘,
így
PQ''R▵∼RAF▵ésP''Q''R▵∼RAF''▵,
mert megfelelő oldalaik páronként merőlegesek. Így
12=PQ''P''Q''=PQ''Q''R⋅Q''RQ''P''=RAAF⋅AF''RA=AF''AF,
azaz
AF''=12AF;
tehát AF'' és így a vele egyenlő FF' is független a P' ponttól és fele az eredeti parabola megfelelő adatának. P' tehát parabolát ír le, melynek paramétere feleakkora, mint az eredeti paraboláé, és ez volt a bizonyítandó.
*

A versenybizottság megállapításai közül röviden csak a következőket említjük meg a tanulóifjúság okulására: az 1. feladatban a formális számolást elég jól végezték, de a tanulók túlnyomó része még mindig tévesen így okoskodott: helyes következtetésekkel, helyes eredményre jutottunk, tehát a kiindulás helyes. A 2. feladat bizonyult legkönnyebbnek. Itt sokan használták fel az I. osztályú tankönyvet, vagy a K. M. L. 501. sz. feladat megoldását (1953 október), de ‐ sajnos ‐ igen sok megoldásnál hiányzik a szerkesztést indokoló szöveg és igen sok versenyző nem törődött a megoldások számával. A 3. feladat okozta a legtöbb nehézséget. Igen sok IV. osztályú tanuló hozzá sem fogott, amíg szép számmal akadt III. osztályú tanuló, aki ‐ ha ≫nem is tanulta még a parabolát≪ ‐ az y=ax2 másodfokú fügvény képéből oldotta meg a feladatot. Elég gyakoriak voltak az elemi megoldások is, bár itt sok, az ábrákból leolvasott, állítás maradt szigorú bizonyítás nélkül.
Egyébként a bizottság a III. osztályosok dolgozatainak elbírálásánál figyelembe vette, hogy az illető tanuló a koordinátageometriai órákon még nem tanult a paraboláról, bár a Rákosi versenyre komolyan készülő tanulóktól elvárható, hogy az osztályban elvégzett tananyagon túlmenően is érdeklődjenek a tankönyvből a tanév még hátralévő tananyaga iránt.
1A gimnáziumok közül 1 szakéretts. tanf. 8 tanulóval, akik közül 1 került a döntőbe

2Legyen e egy PR-től különbözd egyenes P-n át. Ennek azon félegyenesének pontjai mely P-ből indulva a direktrix és PR közti hegyes szögtérbe lép, könnyen láthatóan a fókusztól vannak távolabb, mint a direktrixtől, viszont messe az F-ből e-re bocsátott merőleges a direktrixet Q'-ben. Emeljünk Q'-ben a direktrixre merőlegest, messe ez FQ' felezőmerőlegesét, illetőleg e-t a T, ill. U pontban, akkor belátható, hogy T'Q' és U közt van FT=TQ' s így FU<FT+TU=Q'T+TU-Q'U, vagyis U a fókuszhoz van közelebb, mint a direktrixhez, tehát e átmetszi a parabolát.

3Úgy is látható ez, hogy az S pontok az eredeti parabolának az F pontból felére kicsinyített képét alkotják.