Cím: 1953. évi Kürschák József matematikai tanulóverseny feladatainak megoldása
Szerző(k):  Hajós György 
Füzet: 1954/március, 65 - 73. oldal  PDF  |  MathML 
Témakör(ök): Kürschák József (korábban Eötvös Loránd)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Első feladat. Adva van az n természetes számnál kisebb s egymástól különbözö természetes számoknak egy sorozata, adva van továbbá egy másik ugyanilyen tulajdonságú sorozat. Bizonyítandó, hogy ha a két sorozat elemeinek együttes száma legalább n, akkor található a két sorozatnak egy-egy eleme, melyeknek összege éppen n.
I. megoldás. Tegyük fel, hogy nincs a két sorozatnak egy-egy, egymást n-re kiegészítő eleme. Ebben az esetben, ha az első sorozat elemei a1, a2, ..., ak, a második sorozatban az n-a1, n-a2, ..., n-ak számok nem szerepelhetnek. Az 1, 2, ..., n-1 számok közül e k darab számot elhagyva n-k-1 darab szám marad. A második sorozatban csak ezek szerepelhetnek. A két sorozat elemeinek együttes száma tehát legfeljebb k+(n-k-1)=n-1.
Mivel azonban az elemek együttes száma legalább n, feltevésünk lehetetlen, azaz a feladat állítása helyes.

 

II. megoldás. Alkossunk egy újabb sorozatot azokból a számokból, amelyek a második sorozat elemeit n-re egészítik ki. Ebben szerepelnie kell az első sorozat valamelyik elemének, mert e két sorozatnak együttesen ugyancsak legalább n eleme van, az 1, 2, ..., n-1 számokból pedig nem lehet n különbözőt kiválasztani. Az első sorozatnak így megtalált eleme n-re egészíti ki a második sorozatnak egy elemét.
 

Megjegyzések: 1. A közölt két megoldás lényegében azonos gondolatra épül. Egybevetésük mégis tanulságos lehet.
2. Fel lehet vetni a kérdést, hogy ha nem két, hanem s sorozat szerepel, mekkorának kell akkor lennie együttes elemszámuknak ahhoz, hagy bizonyosan legyen közöttük két sorozatnak egy-egy olyan eleme, melyeknek összege n. Ez a minimális elemszám n+(s-2)m, ahol m az n2-nél kisebb egész számok legnagyobbikát jelenti. Ennek bizonyítását az olvasóra hagyjuk.
 

Második feladat: Legyen n természetes szám, s legyen d osztója 2n2-nek. Bizonyítandó, hogy n2+d nem négyzetszám.
 

I. megoldás. Legyen 2n2=kd, ahol a feltevés értelmében k pozitív egész szám. Ha n2+d négyzetszám, akkor valamely x egész számra
x2=n2+d=n2+2n2k,
s ebből következőleg
k2x2=n2(k2+2k).
Ez azonban lehetetlen, mert a baloldal teljes négyzet, a jobboldal első tényezője is; viszont a második tényező nem teljes négyzet, hiszen
k2<k2+2k<(k+1)2,
azaz két szomszédos négyzetszám fogja közre.
 

Megjegyzések: 1. Amikor megállapítottuk, hogy k pozitív, arra építettünk, hogy a feladat csak természetes számokról szól. A feladat szövegezése kifogásolható, mert kifejezetten nem mondja, hogy az állítás csak pozitív d osztókra vonatkozik. Ilyen megszorítás nélkül nem is helyes a feladat állítása, mert d=-n2 osztója 2n2-nek, s ekkor n2+d=0, ami 0-nak négyzete. Minden más negatív osztóra teljesül a feladat állítása. Ez belátható, ha megtartjuk a megoldás jelöléseit, de most feltételezzük, hagy k negatív egész szám. Ha k=-1, akkor k2+2k=-1 nem négyzetszám; ha k=-2, láttuk, hogy az állítás nem teljesül. Ha viszont k<-2, akkor
(k+2)2<(k+2)2+2(-k-2)=k2+2k<(k+1)2,
s ezért k2+2k ismét nem lehet négyzetszám.
2. A megoldásban hivatkoztunk arra a tényre, hogy ha a, b, c természetes számok, és a2=b2c, akkor c szükségképpen négyzetszám. Ez következik abból, hogy a természetes számok egyféleképen bonthatók fel törzsszámok szorzatára. Emiatt a2 és b2 felbontásában minden törzstényező páros kitevővel szerepel, mert a négyzetreemelés ilyen törzsfelbontáshoz vezet. Így tehát, az a2:b2 osztás elvégzésével, c-nek olyan felbontását kapjuk, melyben minden törzstényező páros kitevővel szerepel. Ezért c négyzetszám.
 

II. megoldás. Legyen újból 2n2=kd. Ha a feladat állítása hamis, akkor valamely x egész számra
k+2k=n2+dn2=x2n2.
A baloldali tört számlálójának s nevezőjének különbsége 2, s e különbség a tört egyszerűsítése után csak csökkenhet. A jobboldali tört egyszerűsítésével p2q2 alakú törthöz jutunk, ahol p és q természetes számok, s ezek nem lehetnek egyenlők mert n2+d≠n2. Ez utóbbi tört számlálójának és nevezőjének különbsége viszont legalább 3, mert felírható p és q összegének és különbségének szorzataként, két egymástól különböző természetes szám összege pedig legalább 3, különbségük meg legalább 1. A fenti egyenlőség tehát nem teljesülhet.
 

Megjegyzés: Amikor megállapítottuk, hogy p és q nemcsak egész számok, hanem pozitív egész számok, akkor kirekesztettük a tárgyalásból azt a lehetőséget, hogy az egyenlőségünkben szereplő törtek értéke 0. Bizonyításunk tehát k=-2 kivételével k minden egész értékére helytálló (összhangban korábbi megjegyzésünkkel).
 

III. megoldás. Ha a feladat állítása hamis, akkor van egy legkisebb olyan n természeten szám, amelyhez található az állítást cáfoló d szám. Kimutatjuk, hogy ennek az n-nek és d-nek nem lehet közös p törzstényezője: Ellenkező esetben ugyanis p osztója (n2+d)-nek; és mivel ez négyzetszám, p2 is osztója (n2+d)-nek; akkor p2 osztója d-nek is, mert n2-nek osztója; tehát az n-nél kisebb np számra és négyzete kétszeresének dp2 osztójára
(np)2+dp2=n2+dp2
négyzetszám, ami ellentmond n megválasztásának.
Így tehát csak azzal az esettel kell foglalkoznunk, amikor d és n relatív prím. Ez esetben d csak úgy lehet 2n2-nek osztója, ha 2-nek is osztója. Ezért d értéke csak 1 vagy 2 lehet. Viszont sem n2+1, sem n2+2 nem lehet négyzetszám, hiszen az n2-re következő első négyzetszám (2n+1)-gyel nagyobb, ami 2-nél több. Lehetetlen tehát az, hagy feladatunk állítása hamis legyen.
 

Megjegyzések: 1. Ha ennél a megoldásnál is kiterjesztjük figyelmünket a negatív osztókra, akkor n2-1 és n2-2 is vizsgálandó. Könnyű megállapítani, hogy közülük csak n2-1, s csak akkor lehet négyzetszám, ha értéke 0. Ez megfelel korábbi megjegyzéseinknek.
2. Felvetjük a kérdést, hogy vajon igaz marad-e a feladat állítása, ha abban 2n2 helyett n2-nek más többszöröse szerepel. Utolsó megoldásunkból látjuk, hogy 2n2 azért felel meg, mert sem 2, sem annak osztója nem írható fel két természetes szám négyzetének különbségeként. Van-e más ilyen tulajdonságú N természetes szám? Minthogy 2k+1=(k+1)2-k2, azért N-nek nem lehet páratlan törzstényezője, N csak 2-nek hatványa lehet. Mivel pedig 8=32-12, azért N nem lehet 2-nek sem köbe, sem magasabb hatványa. Tehát N csak 1, 2 vagy 4 lehet. Ezek a számok meg is felelnek: 1-ről és 2-ről már beláttuk; 4 is megfelel, ugyanis n2+4 sem lehet négyzetszám, mert n2 és (n+2)2 közrefogja, viszont (n+1)2 és n2+4 sohasem egyenlő, hiszen különbségük páratlan. Ezzel tehát a feladat állításán túlmenően igazoltuk, hogy ha n természetes szám, és d osztója 4n2-nek, akkor n2+d nem négyzetszám.
 

Harmadik feladat. Az egyenlőoldalú ABCDEF konvex hatszög A, C, E szögpontjainál elhelyezkedő szögek összege a B, D, F szögpontoknál elhelyezkedőknek összegével egyenlő. Bizonyítandó, hogy az A és D, továbbá a B és E, valamint a C és F szögpontoknál lévő szögek egyenlők.
 

I. megoldás. Először azt bizonyítjuk, hogy a BDF▵ hegyesszögű. Legyen az egyenlőoldalú ABCDEF hatszög belsejében elhelyezkedő BDF▵ derékszögű vagy tompaszögű. Legyen DF e háromszög leghosszabb oldala (1. ábra).
 
 
1. ábra
 

A DEF▵-ből látható, hogy a hatszögoldal DF felénél nagyobb, s így még inkább nagyobb, mint a BF, BD befogójú derékszögű háromszög átfogójának fele. A hatszögoldallal, mint sugárral írt körben a BF, BD húrokhoz tartozó középponti szögek a hatszög A∢-ével és C∢-ével egyenlők. A mondott átfogó, mint átmérő fölé írt körben viszont az ugyanakkora húrokhoz tartozó középponti szögeknek összege 180∘. Ezek szerint A∢+C∢<180∘, hiszen nagyobb sugarú körben ugyanakkora húrhoz kisebb középponti szög tartozik. Így tehát A∢+C∢+E∢<360∘, s a hatszög másik három szögének összege 360∘-nál nagyobb, minthogy a hatszög szögösszege 720∘. Feladatunknak szögekre vonatkozó kirovása tehát nem teljesülhet, ha a BDF▵ nem hegyesszögü.
Jelölje r a hegyesszögü BDF▵ köré írt kör sugarát, és O a középpontját. Ez a háromszög belsejében van. A hatszöget közös O csúccsal bíró hat háromszögre bontjuk fel (2. ábra).
 
 
2. ábra
 

Nem lehetséges az, hogy a hatszögoldal r-nél nagyobb legyen, mert ellenkező esetben a mondott hat háromszög mindegyikében kisebb volna az A, C, ill. E csúcsnál lévő szög, mint az O-nál elhelyezkedő, hiszen a szemközti oldalakra ilyen egyenlőtlenség állna fenn, így pedig az A∢+C∢+E∢ összeg az O körül elhelyezkedő szögek összegénél, 360∘-nál kisebb volna, ami ‐ mint láttuk ‐ lehetetlen. A hatszögoldal nem lehet r-nél kisebb sem. Ez ugyanúgy látható be, csak okoskodás közben ellentétes egyenlőtlenségek szerepelnek.
A hatszögoldal ezek szerint r-rel egyenlő. Ezért ABOF és EDOF rombusz-és AB∥FO∥ED. Ugyanúgy adódik, hogy a hatszög szemközti oldalai valamennyien párhuzamosak, s ezért a szemközti szögek egyenlők.
 

Megjegyzés: Az 1. ábrán szereplő hatszög nem konvex. Bizonyítás nélkül megjegyezzük, hogy az egyenlő oldalú ABCDEF hatszög nem is lehet konvex, ha a BDF▵ nem hegyesszögű. Megoldásunk első része tehát úgy is zárulhatott volna, hogy ha a BDF▵ nem hegyesszögű, akkor nem teljesülhet a feladatnak a hatszög konvexitását követelő kirovása sem.
 

II. megoldás. Először a következő segédtételt bizonyítjuk: Ha α+β+γ=180∘, és α1+β1+γ1=180∘, továbbá
sinα:sinβ:sinγ=sinα1:sinβ1:sinγ1,
akkor α=α1, β=β1, γ=γ1. Készítsünk ugyanis két háromszöget, az egyiket α, β, γ, a másikat α1, β1, γ1 szögekkel. A sinus-tétel értelmében a sinusok arányainak egyezése azt mondja ki, hogy háromszögeink oldalainak aránya megegyezik. E háromszögek tehát hasonlók és megfelelő szögeik valóban egyenlők.
Legyenek most már a hatszög A, C, E csúcsainál levő szögek rendre 2α1, 2β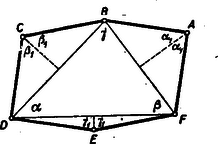1, 2γ1 (3. ábra).
 
 
3. ábra
 

A hatszög szögösszege 720∘, a feladat kirovása értelmében tehát 2α1+2β1+2γ1=360∘, és így α1+β1+γ1=180∘. Ha a hatszög oldala a, a BDF▵ oldalai 2asinα1, 2asinβ1, 2asinγ1. Innen és a sinus-tételből következik, hogy a segédtételünkben szereplő arányhármasok mindegyike a BDF▵ oldalainak arányát adja. Ezért ezek az arányhármasok egyenlők, és segédtételünk értelmében α=α1, β=β1, γ=γ1. A hatszög szemközti szögei egyenlők, mert pl. a D-nél lévő szöge α-nak és a β1, γ1 szögek pótszögei összegének, azaz α1-nek összege, tehát az A-nál lévő szöggel egyenlő.
 

III. megoldás. Hatszögünkből három átlóval három egyenlő szárú háromszöget vágunk le (4. ábra).
 
 
4. ábra
 

Ezek csúcsainál levő szögeknek összege a feladat kikötése folytán 360∘. Ezért e háromszögek egyetlen háromszöggé rakhatók össze. Az így kapott háromszög az oldalak egyezése miatt egybevágó azzal a háromszöggel, amelyik hatszögünkből a három egyenlő szárú háromszög levágása után megmaradt. A három egyenlő szárú háromszöget elhelyezhetjük tehát a hatszögünkből megmaradt háromszögön. Ezzel a hatszöget három (két-két egyenlő szárú háromszög alkotta) rombuszra bontottuk. Ebből közvetlenül adódik, hogy a hatszög szemközti oldalai párhuzamosak és szemközti szögei egyenlők.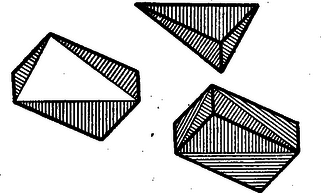
 
 
5. ábra
 

Megjegyzés: Ez a megoldás ‐ mint az 5. ábra mutatja ‐ alkalmazható a feladatban kimondott tétel következő általánosításának bizonyítására is: Ha egy konvex hatszög szemközti oldalai páronként egyenlők, továbbá három páronként nem-szomszédos szögének összege a másik három szög összegével egyenlő, akkor szemközti szögei páronként egyenlők. Következő megoldásainkban mindjárt ennek az általánosabb tételnek bizonyításával foglalkozunk. Ez munkatöbbletet nem okoz.
 

IV. megoldás. Egy hatszög megadásához nyilván elégséges oldalainak hosszát és három páronként nem-szomszédos szögét megadni. Ha a feladat szögekre vonatkozó kirovásának teljesülése folytán tudjuk, hogy három ilyen szög összege 360∘, akkor természetesen elegendő közülük csak kettőt adni meg.
Legyen adva egy konvex hatszög, amelynek szemközti oldalai páronként egyenlők, s amelyik eleget tesz a feladat szögekre vonatkozó kirovásának. Készítsünk egy négyszöget, melynek három oldala a hatszög három csatlakozó oldalával egyenlő, s amelyben az e három oldal által közrefogott két szög a hatszögnek azzal a két nem-szomszédos szögével egyenlő, melyeket rendre ugyanakkora oldalak fognak közre (6. ábra).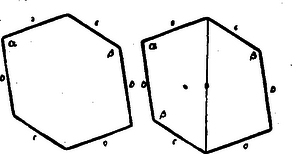
 
 
6. ábra
 

Tükrözzük ezt a négyszöget a negyedik oldal felezőpontjára. Így egy centrálszimmetrikus hatszöget kapunk, amelynek szemközti szögei a szimmetria folytán egyenlők, s amely ezért eleget tesz a feladat szögekre vonatkozó kirovásának.
Az adott hatszög az előrebocsátott megjegyzés értelmében egybevágó az így kapott hatszöggel. Ezért az adott hatszög szemközti szögei is egyenlők.
 

V. Megoldás. Az adott konvex hatszög szemközti oldalai egyenlők, és három páronként nem-szomszédos szögének összege 360∘. Síkbeli mozgatással elhelyezhető tehát e hatszög három helyzetben úgy, hogy a mondott három szög egy teljes szöget alkosson.
 
 
7. ábra
 

A 7. ábra jelölését használva megállapíthatjuk, hogy A1A2C2C1 és A2A3C2C1 paralelogramma, mert szemközti oldalaik a hatszögek egybevágósága miatt egyenlők. Így tehát az A1, A2, A3 pontok egy egyenesen vannak. Ugyancsak az egybevágóság miatt B1A1A2∢=B2A2A3∢. Ezért A1B1∥A2B2. Tehát a hatszög szemközti oldalai párhuzamosak és szemközti szögei egyenlők.
 

VI. megoldás. A 7. ábra jelöléseit használjuk. Feltesszük, hogy A1B1, és A2B2 nem párhuzamos. Legyen tehát az A1B1B2A2 négyszög A1 és A2 csúcsú szögeinek összege 180∘-nál kisebb (ellenkező esetben az A1, A2 és B1, B2 pontok szerepét felcserélnők). A 7. ábrát a C2 szögletbe illesztett negyedik, ugyancsak az adott hatszög síkbeli mozgatásával kapott hatszöggel egészítjük ki (8. ábra).
 
 
8. ábra
 

Ez lehetséges, mert az adott hatszög három-három páronként nem-szomszédos szögének összege 360∘.
Forgassuk el a H1 hatszöget az A1, A2, A3 pontokon áthaladó k kör középpontja körül úgy, hogy az A1 pont A2 helyzetbe jusson. A hatszögek egybevágósága miatt A1A2=A2A3. Ebből következik, hogy az elforgatás során az A1A2 szakasz A2A3 helyzetbe, a H1 hatszög H2 helyzetbe, a H3 hatszög tehát H4 helyzetbe jut. Ezért a C1, C2, C3 pontok egy k-val koncentrikus k1 körön vannak.
Állítjuk, hogy a C1 pont s így a k1 kör is k belsejében van. A H1, H2 hatszögek A2-nél elhelyezkedő szögeinek összege 180∘-nál kisebb. Ezért az A2B2 félegyenes k belsejébe indul és k-nak valamely A2E2 húrját tartalmazza (9. ábra).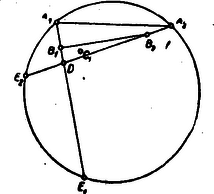
 
 
9. ábra
 

Ebből k középpontja körül való elforgatással az A1B1 félegyenes által tartalmazott A1E1 húrt kapjuk. E két húr egymást a körön belül egy D pontban metszi, hiszen B1 és B2 az A1A2 egyenesnek ugyanazon az oldalán van, így ez az E1 és E2 pontokra is áll, a húrok végpontjai tehát A2, A1, E2, E1 rendben következnek a k körön az elforgatás következményeként. Ezek szerint az A1A2D▵ a k körön belül van, s a konvexitás miatt e háromszög tartalmazza a C1 pontot. Ezzel a fenti állítást igazoltuk.
A H1, H2 hatszögek alakzatának a H3, H4 hatszögek alakzatával való egybevágóságából azonban az következik, hogy a k és k1 körök sugara egyenlő. Ez az ellentmondás feltevésünk lehetetlenségét bizonyítja. Hatszögünk szemközti oldalai tehát párhuzamosak és szemközti szögei egyenlők.
 

Megjegyzések: 1. A 8. ábrát újabb hatszögek csatolásával tovább építhetjük, így az egész síkot beborító hatszögrácshoz juthatunk (10. ábra).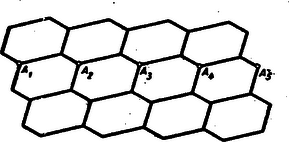
 
 
10. ábra
 

A szemlélet azt mutatja, hogy ennek a rácsnak hatszögei egymást sem részben, sem egészben nem fedhetik. E tény szabatos igazolása nem illenék már e lap keretei közé. Megjegyezzük azonban, hogy ebből a tényből egyszerűen következik a feladat állítása. Elég ugyanis azt belátni, hogy az A1, A2, A3, ... pontok egy egyenesen vannak. Ennek így kell lennie, mert ellenkező esetben egy körön helyezkednének el, hiszen az A1A2A3... töröttvonal szakaszai és ezek hajlásszögei a hatszögek egybevágósága miatt egyenlők. Ha viszont e pontok egy körön volnának, akkor volnának olyan hatszögek is, amelyek egymást részben vagy egészben fedik.
2. Elkészíthetjük a mondott hatszögrácsot akkor is, ha az adott hatszög konkáv (11. ábra).
 
 
11. ábra
 

A szemléletre építve, de szabatos bizonyítás nélkül ugyanúgy következik ebből az ábrából, hogy feladatunk állítása és ennek csak a szemközti oldalak egyenlőségét megkövetelő általánosítása akkor is helyes, ha a hatszög konvexitását nem kötjük ki.
3. A közölt megoldások mindegyike kihasználja a hatszög konvexitását. Ez történt, amikor a hatszöget átlókkal daraboltuk, amikor szögeiket átlókkal felbontottuk, amikor a 6. ábra négyszögének szerkesztésénél természetesnek vettük, hogy oldalai nem metszik egymást, és amikor a 7. ábrával kapcsolatosan hallgatólag kihasználtuk azt, hogy pl. az A1A2C2C1 négyszög oldalai nem metszhetik egymást.
 

VII. megoldás. Az adott hatszöget AD átlójával két négyszögre bontjuk. Tükrözzük az ABCD négyszöget az AD oldal felezőpontjára. Így a centrálszimmetrikus ABCDE1F1 hatszöghöz jutunk, melynek szemközti szögei egyenlők. Elég tehát kimutatnunk, hogy e hatszög az adott hatszöggel azonos.
Ellenkező esetben ugyanis pl. DAF∢<DAF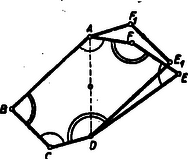1∢ (12. ábra).
 
 
12. ábra
 

Mivel a DAF▵-ben és DAF1▵-ben páronként egyenlő oldalak különböző szögeket fognak közre, a kisebbik szöggel szemben a harmadik oldalak kisebbike van, tehát DF<DF1. Ugyanarra a tételre hivatkozva a DEF▵ és DE1F1▵ esetében: DEF∢<DE1F1∢. Ezek szerint az adott hatszög A, C, E csúcsú szögeinek összege kisebb a másik hatszög megfelelő szögeinek összegénél, 360∘-nál. Ezért a feladatnak a szögekre vonatkozó megkötése a vizsgált esetben az adott hatszögre nem teljesülhet.
 

Megjegyzések: 1. Valamennyi eddig közölt megoldás felhasználta a sokszögek szögösszegére vonatkozó ismereteinket, tehát lényegesen épített a párhuzamosság axiómájára. A legutóbbi megoldást úgy módosíthatjuk, hogy ebben a vonatkozásban csak a következő segédtételre építsen: Ha két háromszögben két-két oldal páronként egyenlő, akkor az ezekkel szemben levő szögeknek összege abban a háromszögben nagyobb, amelyikben a két oldal által közrefogott szög kisebb. E segédtétel helyessége közvetlenül adódik, ha tudjuk, hogy a háromszög szögösszege 180∘. Ha ezt a segédtételt felhasználjuk, befejezhetjük a legutóbbi megoldást anélkül, hogy a hatszög szögösszegére hivatkoznánk. Megállapíthatjuk ugyanis, hogy a DAF▵ és DEF▵ mindegyikében nagyobb a D és F csúcsú szögeknek összege, mint a DAF1▵, ill. DE1F1▵ megfelelő szögösszege. Így tehát az adott hatszögben a 12. ábrán két ívvel jelzett szögeknek összege nagyobb, az egy ívvel jelzetteké pedig kisebb, mint a szimmetrikus hatszög megfelelő szögösszege. Mivel azonban ez utóbbiban a két szögösszeg egyenlő, az adott hatszögben a feladat kirovása nem teljesülhet.
2. Az ismertetett módosítás azért értékes, mert a felhasznált segédtételt a párhuzamosság axiómájára való hivatkozás nélkül is igazolhatjuk. Legyen az ABC▵-ben és A1B1C1▵-ben AB=A1B1, BC=B1C1, továbbá ABC∢>A1B1C1∢. Igazolnunk kell, hogy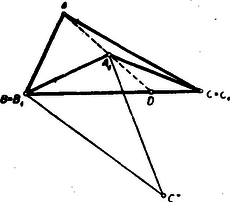
CAB∢+ACB∢<C1A1B1∢+A1C1B1∢.
Nyilván elég azzal az esettel foglalkoznunk, amidőn a baloldali szögeknek egyike nagyobb a jobboldal megfelelő szögénél, pl. amidőn ACB∢>A1C1B1∢. Helyezzük egymásra háromszögeink BC és B1C1 oldalát (13. ábra).
 
 
13. ábra
 

Egyenlőtlenségeink következtében A1 az ABC▵ belsejében van, ezért C1A1B1∢>CAB∢, továbbá az AA1 egyenes által kimetszett D pont a BC szakasz belsejében van. Forgassuk el az ABC▵-et B körül A1BC*▵ helyzetbe. Az adódó ábrában
C1A1B1∢-CAB∢=CA1C*∢,ACB∢-A1C1B1∢=ACA1∢.



Állításunk tehát ACA1∢<CA1C*∢ alakban írható. Ennek helyessége a két-két egyenlő oldalt tartalmazó ACA1▵-ből és CA1C*▵-ből következik, ha tudjuk, hogy AA1<CC*. Ez viszont nyomban adódik, ha az ABA1▵-re és CBC*▵-re alkalmazzuk a következő tételt: Ha két egyenlőszárú háromszög szárai ugyanakkora szöget alkotnak, akkor annak a háromszögnek az alapja nagyobb, amelyiknek szára nagyobb. A szárakra ugyanis BA=BA1<BD<BC.
3. Megállapításainkból következik, hogy a feladat állítása és annak csak a szemközti oldalak egyenlőségét megkövetelő általánosítása helyes az olyan geometriában is, amelyikben a párhuzamossági axióma nem érvényes, viszont a legutóbb kimondott tétel helyes. A tájékozott olvasó számára megjegyezzük, hogy ezzel igazoltuk állításunk helyességét a Bolyai-féle geometriában, sőt ‐ ha a negyedfőkörnél nagyobb távolságokat kizárjuk ‐ a gömbi geometriában is.
 

VIII. megoldás. A feladat eddig tárgyalt általánosításán is túlmenően a következőt igazoljuk: Ha egy konvex hatszög szemközti oldalai egyenlők, és valamelyik szöge a szemközti szögnél kisebb, akkor a három-három páronként nem-szomszédos szög összege közül az a kisebb, amelyikben a szemközti szögnél kisebb szög összeadandóként szerepel.
Legyen a feltételeinket kielégitő ABCDEF hatszögben A∢<D∢ (14. ábra).
 
 
14. ábra
 

Minthogy az FAB▵-ben és a CDE▵-ben e szögeket páronként egyenlő oldalak fogják közre, FB<EC, és a másik két szög összege az FAB▵-ben nagyobb. A BEF▵ és EBC▵ két-két oldala egyenlő, viszont a harmadik oldal a BEF▵-ben kisebb, ezért tehát BEF∢<EBC∢, és a másik két szög összege a BEF▵-ben nagyobb. A kimondott szögegyenlőtlenségeket egybefogva éppen azt kapjuk, hogy ábránk egyíves szögeinek összege a kétívesekénél kisebb.
 

Megjegyzések: 1. Mivel csak az előző megoldáshoz fűzött megjegyzésben kimondott segédtételt használtuk, és a párhuzamossági axiómát nem, azért az ott mondottak a most bizonyított erősebb általánosításra is érvényesek.
2. Könnyű belátni, hogy ha egy konvex hatszög szemközti oldalai egyenlők, és egyik szöge is egyenlő a szemközti szöggel, akkor ez valamennyi szögre áll. Ha ugyanis pl. A∢=D∢, akkor ebből az FAB▵ és CDE▵ egybevágósága, majd FB=EC révén a BEF▵ és EBC▵ egybevágósága, tehát hatszögünk centrálszimmetrikus volta következik. Ezt a megjegyzést felhasználva a feladat állításának a következő, valamivel még többet mondó általánosítását mondhatjuk ki: Ha egy konvex hatszög szemközti oldalai páronként egyenlők, és három páronként nem-szomszédos szöge közül az egyik a hatszög szemközti szögénél kisebb, akkor ez a három szög két másikára is áll. Ha ugyanis e három szög egyike kisebb a szemközti szögnél, másika pedig a szemközti szögnél nagyobb vagy azzal egyenlő volna, akkor e három szög összege ‐ a megoldásunkban bizonyított tétel és a fenti megjegyzés értelmében ‐ a másik három szög összegénél egyrészt kisebb, másrészt viszont annál nagyobb vagy azzal egyenlő volna.
 

IX. megoldás. Hivatkozni fogunk arra, hogy ha két konvex négyszög megfelelő oldalai páronként egyenlők, egyiknek két szemközti szögei α és β, a másiknak megfelelő szögei α1 és β1, ha továbbá α<α1, akkor β<β1. Ez nyomban következik, ha a másik két szögpontot összekötő átlóval négyszögeinket két-két háromszögre vágjuk fel. Ugyanis α<α1 miatt a meghúzott átló az első négyszögben rövidebb, mint a másikban. Ebből viszont β<β1 következik.
Állítjuk, hogy ha hatszögünknek három páronként nem-szomszédos szöge közül kettő kisebb a szemközti szögnél, akkor ez a harmadik szögre is áll. Valóban, ha a 14. ábrában A∢<D∢ és C∢<F∢, akkor az előrebocsátott megjegyzést az ABEF és BCDE négyszögekre alkalmazva azt kapjuk, hogy e négyszögeknek E-nél elhelyezkedő szögei rendre kisebbek, mint a másik négyszögnek B-nél lévő szögei. Ezért csakugyan E∢<B∢.
Tudjuk, hogy ha hatszögünknek egy szöge a szemköztivel egyenlő, ugyanez minden szögre is igaz. Ezt az előző megoldáshoz fűzött megjegyzésben bizonyítottuk.
Ezek szerint, ha a konvex hatszög szemközti oldalai egyenlők, akkor három-három nem-szomszédos szöge vagy páronként egyenlő, vagy pedig az egyik szöghármasnak mindegyik szöge kisebb a másik szöghármasnak megjelelő (szemközti) szögénél. Ha ugyanis nem mindegyik szög egyenlő a szemközti szöggel, akkor ‐ mint tudjuk ‐ egyik szög sem lehet a szemköztivel egyenlő. Ebben az esetben a három átellenes szögpárnak kisebb szögei ugyanahhoz a szöghármashoz kell, hogy tartozzanak, mert ellenkező esetben az egyik szöghármas kettőt tartalmazna e kisebb szögek közül, ami a bizonyított állítás szerint lehetetlen.
A bizonyított tétel többet mond ki, mint feladatunk állítása.
 

Megjegyzés: 1. Feladatunk állításának most bizonyított általánosítása csak átszövegezése a legutóbbi megjegyzésben kimondottnak.
2. Ebben az utolsó megoldásban sem a párhuzamosság axiómájára, sem a legutóbbi két megoldásban felhasznált segédtételre nem támaszkodtunk. Megoldásunk bizonyítja, hogy feladatunknak tétele és tárgyalt általánosításainak mindegyike helyes a nem-euklideszi geometriában, a Bolyai-féle geometriában és a gömbi geometriában is.