|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Sok ifjú olvasónk szíve bizonyára hangosabban dobban, ha arra gondol, hogy megnyerheti a Kürschák-versenyt és az egész ország színe előtt megmutathatja hivatottságát és rátermettségét. Az ifjú, aki erről ábrándozik, bizonyára feltette néha magában a kérdést, ki lehetett az a férfiú, akiről ezt a nevezetes versenyt elnevezték. Ezekben a sorokban igyekszem jellemezni Kürschák Józsefet, a nagy matematikust, az ifjúság melegszívű barátját és jóakaróját.
Kürschák József kisiparos családból született 1864 március l4-én Budán. Ámbár a középiskola minden tárgyában kitűnő előmenetelt tanúsított, matematikai tehetsége már középiskolás korában megnyilvánult, mert amikor a tanár egy ábrázoló geometriai tételt adott elő, a bonyolult bizonyítást Kürschák még ott az órán, jóval egyszerűbbel helyettesítette és jeles tanára (Kreybig Lajos) elismerte, hogy a tanuló szerkesztése jobb az előadottnál. 1881-ben került Kürschák a Műegyetemre, amelynek nagyszerű tanárai közül különösen Kőnig Gyula ‐ a magyar matematika múltjának Bolyai János mellett legnagyobb alakja ‐ volt rá nagy hatással, akit mindvégig mesterének tekintett. Kőnig hatása alatt keletkezett egyik legkorábbi műve a legfelsőbb matematika egyik ágából ‐ az úgynevezett parciális differenciálegyenletekről ‐amelynek a fizikai alkalmazásokban is nagy szerepe van. Már ennek a korai műnek is oly nagy sikere volt, hogy amikor Kürschák kevéssel utóbb egy nemzetközi matematikai kongresszuson vett részt, az ifjú tudós nevét már ismerték.
Az egyetemi tanulmányok befejezése után Kürschák középiskolai tanár lett a rozsnyói katolikus gimnáziumban, azután a debreceni, majd a budapesti V. kerületi állami reáliskolában tanított, míg végül hő vágya teljesült és 1891-ben a Műegyetemre került mint repetítor, ahol egyre emelkedve, 1904-ben rendes tanár lett s így őmaga is a Műegyetem kiváló matematikus tanártestületének tagjává vált, 1916-tól 1918-ig a Műegyetem rektori méltóságát töltötte be.
Kürscháknak olyan nyugalom jutott osztályrészül, mint kevés tudósnak. Egész életét (a vidéki tanárkodástól eltekintve) a Hunyadi-út 14. sz. családi házban tölthette. A nyugodt életkörülmények is segítették, hogy veleszületett tehetségét teljesen kifejthesse.
Kürschák tudós munkásságának túlnyomó része a felsőbb matematikára esik, erről ezért itt alig beszélhetek, de állandóan érdeklődött a matematika elemibb részei iránt is, néhány idevágó fontosabb eredményét ismertetni fogom. Az elemi matematika iránt táplált érdeklődése is egyik oka, hogy a tanulóversenyek ügye valóságos szívügye volt.
A Mathematikai és Physikai Társulat 1894-ben az érettségizett tanulók részére versenyt alapított annak örömére és emlékéül, hogy elnöke Eötvös Loránd közoktatásügyi miniszter lett. A versenyt ezért nevezték el Eötvös verseny-nek. Kürschák kezdettől fogva élénken részt vett ezen versenyek előkészítésében, feladatokat tűzött ki, a dolgozatokat megbírálta, hogy milyen szakavatottsággal, azt az mutatja, hogy a verseny győztesei között ─ akikkel szinte baráti viszonyban volt ─ nagyszámú világhírű matematikus akadt. A versenyek iránt mutatott nagy érdeklődésének tanújele pompás könyve a Matematikai versenytételek, Szeged 1929, amelyben az első 32 verseny anyagát dolgozta fel mintaszerűen. Megmutatja valamennyi feladat megoldását, legtöbbször a pályanyertes dolgozatokét. Megmutatja továbbá a versenyfeladatok összefüggését a matematika fontos részeivel. A könyv, amely igazán szórakoztatva tanít, a mai ifjúságnak is a legmelegebben ajánlható.
A két világháború néhány éves szüneteket hozott a versenyekben. A felszabadulás után ‐ amikor Eötvös Loránd nevét természetesen a különváló fizikai társulat és a fizikai verseny vette fel ‐ érthető, az elmondottak alapján, hogy az újjászervezett versenyt Kürschákról nevezték el.
Külön meg kell emlékeznem Kürschák népszerűsítő cikkeiről, amelyekben a matematika nagy haladását igyekezett megismertetni a hazai matematikusokkal. Így a vidéki elhagyatottságban, minden irodalmi forrástól távolélő matematikusoknak felbecsülhetetlen szolgálatokat tett. Így ismertette Hadamard (ejtsd Ádámár ‐ az első két á rövid) a ma is élő nagy francia matematikus ‐ akiről e cikkben még lesz szó ‐ doktori értekezésének korszakalkotó eredményeit. Ily természetű cikkeiben is megnyilvánult nagy érdeklődése az elemi és felsőbb matematika határán lévő kérdések iránt. A körmérés kétezerötszáz éves történetéről szóló cikksorozatára gondolok, amelyben alkalma nyílt megmutatni a legelemibb kérdések összefüggését a felsőbb matematika legújabb vívmányaival. A körmérés elmélete ugyanis azon tény bebizonyításában nyerte megoldását, hogy a szám semmiféle egész együtthatós algebrai egyenletnek sem tehet eleget. Az ilyen számokat transcendens-eknek hívjuk. transcendens voltát csak 1882-ben sikerült bebizonyítania Lindemann német tudósnak. Ezt a bizonyítást 1893-ban három kiváló matematikus különféleképp ugyan, de lényegesen egyszerűsítette. Kürschák cikksorozata ezekhez az akkor teljesen új eredményekhez vezet el.
Példát hozok most fel Kürsehák gondolkozásának gyorsaságára. Waring (ejtsd Uáring) angol matematikus 1770-ben kimondta azt a sejtését, hogy ha tetszésszerinti pozitív egész szám, minden egész szám előállítható mint csak a -tól függő (tehát az előállítandó számtól független) véges számú -ik hatvány összege. Pl. minden szám előállítható mint legfeljebb négyzet, mint legfeljebb köb, mint legfeljebb negyedik hatvány összege stb. Ez a tétel 139 éven át minden bizonyítási kísérlettel dacolt. Csak 1909-ben sikerült Hilbert-nek századunk legnagyobb matematikusának, a tétel bebizonyítása. Hilbert bizonyítása rendkívül komplikált volt. Kürschák a bizonyítást nyomban lényegesen egyszerűsítette, úgyhogy Hilbert második közlésében a bizonyítást már a Kürscháktól származó egyszerűsített alakban adja. Azóta több tudós fáradozásai folytán (köztük a szovjet Vinogradov és a magyar Erdős Pál) a tétel bizonyítása elég egyszerűvé vált. A Waring-tétel a mai számelmélet egyik legfontosabb témája.
Kürschák felsőbb matematikai irodalmi munkásságából már csak egy további adatot említek, amely mutatja, hogy mily nagy nemzetközi megbecsülésnek örvendett. A múlt század végén ugyanis a német tudósok egyesülve hatalmas, munkába kezdtek. Matematikai enciklopédiát indítottak meg (Encyklopädie der mathematisehen Wissenschaften), amely eredetileg azt akarta megmutatni, milyen fejlődési fokot ért el a matematika a századfordulón. A sok kötetnyi mű azonban lényegesen túlnőtt a terven és félévszázadnyi munka után csak nemrég fejeződött be ‐ de az új átdolgozás máris megindult. A mű jelentőségét a francia tudósok is felismerték, úgyhogy a munkát franciául is ‐ lényegesen kíbővítve, hiszen a tudomány időközben is haladt ‐ kiadták, sőt mondhatni újraírták. A francia enciklopédia leglényegesebb fejezetei egyikének, mely jóformán egy egész kötet, megírását a már említett Hadamard-ra és Kürschák-ra bízták.
Mint érdekes epizódot, még azt említem fel, hogy Kürschák egyik munkája Délafrikában jelent meg. A mai magyar matematika igen jelentékeny. Magyar matematikusok műveivel sűrűn találkozunk Európa, Amerika, Ázsia, sőt Ausztrália matematikai lapjaiban, de Afrikában mind e mai napig a magyarok közül egyedül Kürschák publikált.
Áttérek Kürschák néhány elemi matematikai munkájának ismertetésére.
Legelső dolgozata ‐ amelyben azonban már megmutatja oroszlánkörmeit ‐ a körbe és kör körül írt szabályos sokszögekről szól. A tétel ismertetése előtt meg kell ismerkednünk a monoton sorozat fogalmával. Monotonnak nevezünk egy számsorozatot, ha minden tagja egy irányban változik; vagy mind nő, vagy mind fogy. Kürschák megmutatta, hogy a körbe írt -szögek közül a szabályos területe a legnagyobb, a kör köré írtak közül a szabályos területe a legkisebb. Ezzel a tétellel Jakab Steiner hírneves svájci geometer már jóval Kürschák előtt foglalkozott, de Steiner hallgatólag feltételezte, ‐ pedig nem magától értetődő ‐ hogy ilyen maximális, illetve minimális területű sokszög létezik. Kürschák bizonyítása azonban teljesen kifogástalan és azon a segédtételen alapszik, hogy a körbe (körül) írt szabálytalan sokszög területe egyetlen csúcs (oldal) áthelyezésével megnagyobbítható (kisebbíthető). Kürschák tételéből az is következik, hogy ha a körbe írt szabályos szög oldala , a körülírté , akkor az monton nő, míg a sorozat monoton fogy.
Ez az elemi feladat vezette Kürschákot a legfelsőbb matematika egy fontos problémakörére, amely igen jelentékeny eredményeket köszönhet Kürscháknak. Ez a sokszögtétel ugyanis lényegében egy több változós függvény szélső értékeinek meghatározását adja. Az ilyen feladatok közelfekvő általánosítása, oly függvények, vagy a geometria nyelvén szólva görbék keresése, amelyek valamely tulajdonsággal a legnagyobb vagy legkisebb mértékben rendelkeznek. Például Bernoulli Jánossal kérdezhetjük, hogy milyen görbén kell a pontnak mozognia, hogy a (magasabban fekvő) pontból a legrövidebb idő alatt érkezzék (mélyebben fekvő) pontba. A válasz kissé meglepő, mert nem az összekötő egyenesen, hanem cyklois pályán kell a mozgó pontnak haladnia. A felsőbb mennyiségtannak az ilyenfajta kérdésekkel foglalkozó ágát variációszámításnak hívják és ez volt Kürschák tudományos tevékenységének egyik legfontosabb területe. Láttuk, hogy mily szorosan függ össze egy egyszerű elemi geometriai kérdéssel.
Kürschák egyik igen szép elemi eredménye, hogy az sugarú körbe írt szabályos szög területe . Itt sem a tétel új, hanem a bizonyítás, mely minden számítás nélkül ér célt. Kissé egyszerűsítve fogom elmondani. (Ld. az 1. ábrát.) 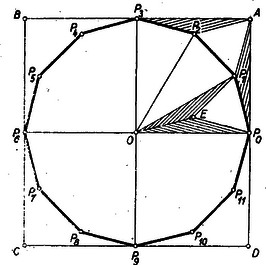 1. ábra
Az középpontú körbe írt szabályos tizenkétszög csúcsai . A körhöz a , , , pontokban rajzolt érintők az négyzetet határozzák meg, melynek területe . Kössük össze -t a tizenkétszög csúcsaival. A tizenkétszög tehát egyenlőszárú háromszögből áll, melyek mindegyikének alapja a tizenkétszög oldala, szára pedig a kör sugara. A tétel be van bizonyítva, ha kimutatjuk, hogy az oldalú négyzet területe egyenlő ilyen háromszög területével. A teljes szimmetria miatt elég lesz az első quadransra szorítkozni.
Rajzoljuk meg tehát a , szögfelezőjét és mérjük fel rá a tizenkétszög oldalát: másrészt a szögfelező merőleges a húrra, tehát Azonban így mert az , ill. pontból induló oldalak egyenlők és merőleges szárú szöget alkotnak, melyek mindegyike hegyes szög, tehát egyenlők. Hasonló egyszerűen bizonyítható, hogy Ebből a két összeillőségből levezethető, hogy Ugyanis (1)-ből , (2)-ből , továbbá , mert mindkettő a szabályos tizenkétszög oldala, vagyis a tizenkétszögnek az első quadransba eső részét az oldalú négyzetté kiegészítő ötszög területére
A tizenkétszög tehát három oly négyzet összege, melyek mindegyikének oldala a kör sugara. (Amit az ábra szimmetriájánál fogva úgy is beláthatunk, hogy a négyzetből a tizenkétszögön kívül maradt ötszög területe együtt egyenlő egy kis négyzet területével.)
Most pedig Kürschák egy igen szép számelméleti tételét ismertetem, melyre e sorok írójának egy tétele vezette rá. A tétel így szól:
Egymásra következő (egész) számok reciprok értékeinek összege sohasem egész szám, azaz az összege és semilyen egész számú értékénél sem lehet egész szám. A tétel annál érdekesebb, mert a jobbolali összeg akármilyen nagy lehet, de az egész számokat mindig kikerüli.
Kürschák szellemes bizonyítása az alábbi egyszerű tételen alapszik, amelynek bizonyítását az olvasóra bízzuk. Az számok között mindig van egy, mely -nek magasabb hatványával osztható, mint a többi bármelyike. Nevezzük ezt -nek, -től eltekintve a (4) sor jobboldalán lévő többi nevező legkisebb közös többszöröse -nek -nál csak alacsonyabb hatványával, pl. -val osztható , tehát összegük alakú, ezért | |
alakú, márpedig páratlan számláló nem lehet -nal osztható. Q. c. d.
Kürschák tételének érdekességét továbbá emeli, hogy Erdős Pál, akinek nevét sok olvasónk ismeri, néhány évvel ezelőtt a tételt több tekintetben továbbfejlesztette, pl. megmutatta, hogy a (4) alatti összeg nem lehet egész szám reciprok értéke sem, másodéves egyetemi hallgató korában pedig kimutatta, hogy bármely egész számú tagokból álló számtani sor egymásra következő tagjai reciprok értékeinek összege sem lehet egész szám.
Azt, hogy vannak oly értékek, amelyekkel tetszőleges mellett a (4) alatti érték akármily nagy lehet, bárki könnyen beláthatja. Ehhez elég azt bebizonyítani, hogy ha pozitív egész szám Ha tehát azt akarjuk, hogy valamely előre megadott akármily nagy szúmnál nagyobb legyen, elég ha -t így választjuk meg .
Bizonyítás nélkül említem fel Kürscháknak egy a binomiális együtthatók számelméleti sajátságairól szóló szép tételét.
Régóta ismeretesek a binominális együtthaható következő érdekes sajátságai | |
továbbá, hogy mindig páros és osztható -gyel és -gyel.
Bauer Mihály (szintén Műegyetemünk igen kiváló matematikusa) még egyetemi hallgató korában bizonyította be, hogy ha osztható a prímszámmal, akkor minden pozitív egész értékénél osztható -vel. Kürschák ezt a tételt a következőképp egészítette ki. Ha
akkor minden pozitív egész értékénél osztható -gyel, ha tehát osztható -val, a hatványösszeg is. Látható, hogy ez a tétel Bauer tételét speciális esetként tartalmazza, t. i. ha páros és .
Most pedig Kürscháknak azt a felfedezését fogom ismertetni, amelyet ‐ persze a felfedező nevével ‐ a világ minden matematikusa ismer. Ez a tétel geometriai.
Hilbert, akiről már szó volt, mutatott rá arra, hogy a geometriai szerkesztésekben a körzőnek kétféle szerepe van. A körzőt ugyanis nemcsak körök rajzolására használjuk, hanem sokszor csupán valamely távolság felmérésére, pl. szögfelezésnél, párhuzamos, merőleges szerkesztésénél stb. Kürschák 1902-ben bebizonyította, hogy ezeket a szerkesztéseket ‐ körző nélkül! ‐ pusztán vonalzóval végre lehet hajtani ha e g y e t l e n e g y távolságot fel tudunk mérni. Ezt az eszközt egységátrakónak (Eichmass, étalon) nevezte. Ilyen eszköz pl. a vonalzó, ha rajta két vonalkával valamely távolság van megjelölve.
A rendkívül egyszerű bizonyítás nagy matematikusra vall. Elegendő annyit bizonyítani, hogy valamely adott egyenesen fekvő távolsággal egyenlő hosszúságú távolságot más irányú egyenes tetszőleges pontjából kiindulva pusztán vonalzóval is meg tudunk szerkeszteni, ha egyetlenegy ‐ természetesen az adottól különböző ‐ távolságot át tudunk vinni.
A bizonyítás felhasznál egy tételt, amely versenyfeladat gyanánt is szerepelt így bizonyítását olvasóinkra bízzuk. Ez a segédtétel a következő:
Ha az és csúcsaiból húzott tranzverzálisok az -ból kiinduló súlyvonalon metszik egymást, a szemközti oldalt pedig a ill. pontban találják. Akkor
Ezen tétel segítségével nyomban szerkeszthetünk pusztán vonalzóval és egységátrakóval adott ponton át adott egyeneshez párhuzamost (2. ábra). 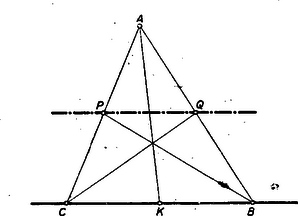 2. ábra
Az adott egyenes tetszésszerinti pontjából jobbra-balra felmérjük a mértékegységet, a végpontok legyenek és . A egyenesen felvesszük egy tetszésszerinti (-től és -től különböző) pontot. -ből a és metszéspontján át húzott egyenes -t messe -ban, a keresett párhuzamos. (Ugyanis az háromszög súlyvonala.)
Ezen előzmények után könnyen bebizonyíthatjuk Kürschák távolságátrakó szerkesztését. Rakjuk át ‐ pusztán vonalzóval és mértékegységgel ‐ az egyenesen megadott távolságot a pontból kiinduló egyenesre: (3. ábra). 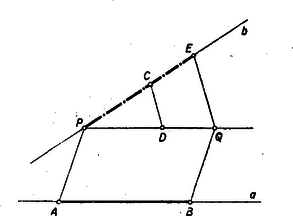 3. ábra
-ből párhuzamosat szerkesztünk -hez (ezt a segédtétel értelmében eszközeinkkel megtehetjük), -ből pedig -hez, metszéspontjuk . Most -ből felmérjük az egységet -re és a egyenesre, a két végpont és . ( ) -ból -hez húzott párhuzamos -t a keresett pontban metszi, tehát
Már csak egyetlen további Kürschák-féle eredmény bemutatására szorítkozom. Olvasóink bizonyára ismerik a sakktáblára vonatkozó következő feladatot: a sakktáblán valamely mezőből kiindulva a tábla minden mezejét be kell járnunk lóugrás szerint úgy, hogy minden mezőt csak egyszer érintsünk.
Kürschák bebizonyította, hogy ez a feladat akkor is megoldható, ha a sakktábla mindkét irányban a végtelenbe terjed. Bizonyítása meglepően egyszerű. A bejárás az mezejű sakktáblán könnyű feladat. Felbontja a végtelen mezőt mezejű táblák összegére.
Kürschák kiváló tanár volt, rendkívül világos előadásával gondolatébresztően hatott, műegyetemi előadásai könyvalakban is megjelentek (Analízis és geometria 1., 1919); ez kitűnő bevezetés a felsőbb mennyiségtanba. Az idősebb mérnökök és a nagy magyar matematikus nemzedék túlnyomó részének nagyrabecsült mestere volt. A matematika története is érdekelte, Bolyai Farkas Tentamen-je gyönyörű új kiadásának egyik szerkesztője.
Még egy nagy szolgálatot tett Kürschák a magyar matematikának. A tudományoknak ‐ köztük a matematikának ‐ a 19. században való rohamos haladása következtében egy-egy személy már nem követhette a tudomány fejlődését. Oly folyóiratokat kellett tehát kiadni, amelyek tárgykörök szerint csoportosítva röviden ismertették az elért új eredményeket. A magyar nyelvű közleményekkel hosszú ideig nem törődött senki. 1902-ben Kürschák egy ilyen francia nyelvű hollandiai referáló (cikkeket ismertető) folyóirat munkatársa lett és azóta a magyar nyelvű matematikai munkákról is tudomást szerzett a világ.
A verseny történetével külön cikkben foglalkoztam e Lap hasábjain 2. évf. (1950) 3‐7. old., azért itt nem részletezem.A versenyre vonatkozó ezt a feladatot ma Hajós György Kossuth-díjas egyetemi tanár látja el mintaszerűen, aki a verseny eredményhirdetésekor ismerteti a feladatok számos változatos megoldását.Algebrai egyenlet-nek hívjuk az alakú egyenletet.A ma 88 éves haladó tudós a nemzetközi matematikai élet egyik legkimagaslóbb vezéralakja 1952 december havában Bolyai János 150. születésnapja alkalmával Budapesten rendezett ünnepségekre Bolyai munkásságához kapcsolódó dolgozatot küldött.Megjegyezzük, hogy a jelen cikkben felhasznált segédtételekre, melyeknek bizonyítását a Szerző az olvasóra bízta, a következő szám példaanyagában még visszatérünk. ‐ Szerk. |
 PDF | MathML
PDF | MathML 

