Kezdőlap


Cím:	Képek a magyar matematika múltjából 2. (Geöcze Zoárd 1873-1916)
Szerző(k):	Obláth Richárd
Füzet:	1954/január, 1 - 5. oldal	PDF \| MathML
Témakör(ök):	Egyéb írások

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Geőcze Zoárd a legkiválóbb magyar matematikusok egyike, mindazonáltal csaknem élete végéig középiskolai tanár volt. Eleinte 16 éven át egy vidéki alreáliskolában (megfelel a mai általános iskola felső négy évének) tanított, bár sikerrel foglalkozott a matematika igen fontos és mély problémáival.
Geőcze ugyan igen előkelő felvidéki nemesi család sarja, de mivel tanár és tudós, azért korában szegénységre van kárhoztatva, amiért előkelő családja nem tarthatta magához méltónak. Geőcze valóban szörnyű nyomorban élt, vidéki elhagyatottságában, nagyszámú családjával (8 gyermeke volt). Nem csoda, hogy az akkori rendszerben a legnagyobb nélkülözéseket szenvedte. Tanár létére mindamellett nagyszerű szakkönyvtárt szerzett be, hiszen különben vidéken nem foglalkozhatott volna tudománnyal. (Könyvtára ma a szegedi Pedagógiai Főiskola könyvtárának alapja.)

A geometria egyik alapfeladata a görbe vonalak ívhosszának és általuk határolt területeknek, valamint a görbelapú testek felszínének és köbtartalmának meghatározása. A görbe felületek felszínét az integrálszámítás feltalálása óta integrállal határozták meg. Felvettek pontokat a felületen, ezek egy soklapot, poliédert határoznak meg, amelynek lapjai általában háromszögek, amelyeknek persze könnyű a területét meghatározni. Ha tehát a felvett pontok számát minden határon túl növeljük, azaz a beosztást sűrítjük, elérhetjük, hogy egy-egy háromszög tetszés szerint kicsiny legyen, vagyis a poliéder a felülethez simuljon és közel 200 évig azt gondolták, hogy ezen kis háromszögek területe összegének határértéke megadja a görbefelület felszínét. Az 1880-as években azonban Hermann Amandus Schwarz (ejtsd: Svarc) hírneves német matematikus bebizonyította, hogy a szemlélet ebben az esetben csal, mert ez a definíció már igen egyszerű felületek (pl. a körhenger) esetén sem állja meg a helyét.
Tekintsünk egy

h

magasságú egyenes körhengert, alapkörének sugara

r

. A magasságot

n

számú egyenlő részre osztjuk és minden osztópontban az alapkörrel párhuzamos síkot fektetünk. Egy-egy részhenger magassága tehát

\frac{h}{n}

. Minden kör kerületét

m

számú egyenlő részre osztjuk (

m

és

n

egymástól teljesen függetlenek). Az egy-egy részhez tartozó középponti szög tehát

\frac{2 π}{m}

, de a körkerület osztópontjait minden egyes egymásra következő körön

\frac{π}{m}

-mel elforgatjuk, amint ez az 1. ábrán látható.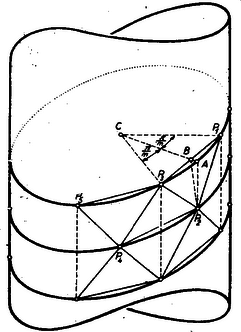

1. ábra

Ha az osztópontokat

P_{1}

P_{2}

P_{3}

...

-mal jelöljük, kapjuk a

P_{1} P_{2} P_{3 △}

P_{2} P_{3} P_{4 △}

P_{3} P_{4} P_{5 △}

, stb. egyenlőszárú háromszögeket. Határozzuk meg ezen egybevágó háromszögek valamelyikének területét.
Ezen háromszögek valamelyikének, pl.

P_{1} P_{2} P_{3}

-nak alapvonala

\begin{matrix} P_{1} P_{3} = 2 r sin \frac{π}{m}, \end{matrix}

magassága

P_{2} B

azonban nem

\frac{h}{n}

, hanem átfogója a

P_{2} A B

derékszögű háromszögnek, melynek egyik befogója

P_{2} A = \frac{h}{n}

, a részhenger magassága, másik befogója pedig

A B

, ahol

A

a körmetszet

\hat{P_{1} P_{3}}

ívének felezőpontja és ha

C

a kör középpontja, az

A C

sugár a

P_{1} P_{3}

húrt

B

-ben metszi. Tehát

\begin{matrix} A B = r - r cos \frac{π}{m} = 2 r sin^{2} \frac{π}{2 m} . \end{matrix}

Ennélfogva a tekintett háromszög területe

\begin{matrix} \frac{P_{1} P_{3}}{2} \cdot P_{2} B = r sin \frac{π}{m} \sqrt[]{\frac{h^{2}}{n^{2}} + 4 r^{2} sin^{4} \frac{π}{2 m}}, \end{matrix}

s mivel a henger felszínén

2 m n

ily háromszög van, azért a háromszögekkel meghatározott poliéder

F

felszíne összesen

\begin{matrix} F = 2 r m n sin \frac{π}{m} \sqrt[]{\frac{h^{2}}{n^{2}} + 4 r^{2} sin^{4} \frac{π}{2 m}} \end{matrix}

(1)

Ha az (1) alatti kifejezésben

n

-t a gyökjel alá visszük, a gyökjel előtti szorzatot

\frac{π}{m}

-mel szorozzuk és osztjuk, a gyökjel alatti második tagot pedig

{(\frac{π}{2 m})}^{4}

-nel szorozzuk és osztjuk,

F

a következű alakot veszi fel:

\begin{matrix} F = 2 r π \frac{sin \frac{π}{m}}{\frac{π}{m}} \sqrt[]{h^{2} + \frac{r^{2} π^{4}}{4} \cdot \frac{n^{2}}{m^{4}} {(\frac{sin \frac{π}{2 m}}{\frac{π}{2 m}})}^{4}} . \end{matrix}

(2)

Bebizonyítjuk a következő segédtételt:

Az egység sugarú körben az

x

ívhez tartozó középponti szög sinusa és az

x

ív aránya tetszés szerint közel kerül 1-hez, hacsak az ív elég kicsiny. Röviden

\frac{sin x}{x}

az 1-hez tart, ha

x

tart 0-ho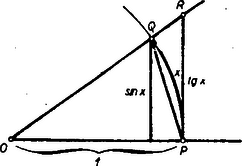z.

2. ábra

A betüzést a 2. ábra mutatja. Az egységsugarú körben (

O P = O Q = 1

) a

P Q = x

ívhez tartozó körcikk területe nyilván az

O P Q_{△}

és

O P R_{△}

területe közé esik, vagyis

\begin{matrix} \frac{sin x}{2} < \frac{x}{2} < \frac{tg x}{2} . \end{matrix}

\frac{2}{sin x}

-szel szorozva

\begin{matrix} 1 < \frac{x}{sin x} < \frac{tg x}{sin x}, \end{matrix}

a reciprok értékeket véve

\begin{matrix} 1 > \frac{sin x}{x} > sin x \end{matrix}

vagyis

\begin{matrix} cos x < \frac{sin x}{x} < 1. \end{matrix}

Mivel ismeretes, hogy

cos x

tetszés szerint kevéssel különbözik 1-től, amint

x

nem nagyobb egy elég kis szögnél, azért a

cos x

és 1 közé eső

\frac{sin x}{x}

szükségképpen szintén tetszés szerint közel kerül 1-hez.

A (2) alatti kifejezésben tehát

\frac{sin \frac{π}{m}}{\frac{π}{m}}

és

\frac{sin \frac{π}{2 m}}{\frac{π}{2 m}}

az 1-hez közeledik, ha

m

minden határon túl nő.

n

is hasonló mértékben növekszik mint

m

, pl.

n

megegyezik

m

-mel, akkor a gyökjel alatti második tagban az első tényező egy állandó szám, a második

\frac{1}{m^{2}}

, a harmadik pedig tetszés szerint közel lesz 1-hez. Így, ha

m

-et elég nagynak választjuk, ez a tag tetszés szerinti kicsiny lesz. A gyökjel előtti szorzatban a törttényező szintén tetszőlegesen közel jut az 1-hez és így az

F

egyre jobban megközelíti a

2 r π h

értéket, ami valóban a hengerpalást felszíne. Ehhez az eredményhez jutunk akkor is, ha

n

-et valamivel gyorsabban növeljük, mint

m

-et, pl.

m

-et

n

2-szeresének, 5-szörösének, 10-szeresének, vagy akár 1000-szeresének, vagy 1 000 000-szorosának választjuk. Más eredményhez jutunk azonban, ha

n

-et még gyorsabban növeljük és pl. mindig éppen

m^{2}

-nek választjuk. Ekkor a gyök alatti második tag nem válik már akármilyen kicsivé, hanem minél nagyobb az

m

, annál kevesebbel fog eltérni az

\frac{r^{2} π^{4}}{4}

értektől,

F

tehát a

2 r π h \sqrt[]{1 + \frac{r^{2} π^{4}}{4 h^{2}}}

értéket fogja egyre jobban megközelíteni, ami már nagyobb, mint a henger felszíne.
De

F

kifejezése minden határon túl is nőhet, ha

n

még rohamosabban nő

m

-hez képest, pl. ha

n = m^{3}

. (Bizonyítsuk ezt be!) Szemléletesen

n

rohamos növelése azt jelenti, hogy az

A P_{2}

befogó aránytalanul kisebb az

A B

befogónál, vagyis a háromszöglapok nem simulnak a henger felszínéhez, hanem meredeken befelé állnak, s ezért lesz összterületük lényegesen nagyobb, mint a henger felszíne.
A leírt sajátságos alakzatot a német matematikus-humor

≫

Knickstiefel

≪

-nek (kihúzható, hajlítható csizma) nevezte, mert ez a poliéder kissé emlékeztet a harmonikára, a lampionra, vagy a hosszabb-rövidebbre húzható csizmaszárra.
A henger felülete azonban, amint azt be lehet bizonyítani, a legkisebb olyan érték, amit az

F

értékek megközelítenek, ha

m

n

is minden határon túl növekszik.

Évtizedeken át nyílt kérdés maradt a görbe felületek felszínének meghatározása. Századunk elején azonban egy szerény ungvári tanár, Geőcze Zoárd mély meggondolásai megtalálták az egyszerűsége ellenére félelmetesen nehéz probléma megoldásához vezető utat.
Magától értetődik, hogy az a gondolkodó, akinek ily alapvető súlyos probléma megoldása sikerül, felfedezését nem akarja titokban tartani, hanem nyilvánosságot keres. Valóban megható a nyomorgó tanár kétségbeesett kapkodása. Először saját költségén kiadott litografált füzetben ismerteti elmélkedéseit, amelyről persze senki nem vett tudomást. Abban az időben középiskoláink évente nyomtatott

≫

Értesítőt

≪

adtak ki, amelyet az iskola valamelyik tanárának tudományos értekezése vezetett be. Ez az ú. n. programmértekezés azonban rendesen a tanulóknak szólt, nem pedig a tudományos világnak. Geőcze ezzel nem törődve, iskolája két ilyen Értesítőjében közölte két munkáját, amelyeknek a legmagasabbrendű tudományos folyóiratokban lett volna a helyük. Az egyikben írja:

≫

az integrál jel technikai okokból mellőztetett

≪

. A technikai ok az volt, hogy a vidéki nyomdának nem volt integrál jele!
1906-ban Ungvárra került egy jóképzettségű fiatal kolléga, aki tanulmányait Kolozsvárott végezte. Ő figyelmeztette Geőczét, hagyja abba a budapesti Műegyetem hírességeivel való reménytelen próbálkozásait, forduljon Kolozsvárra, ahol Schlesinger Lajos nemcsak elsőrangú matematikus, hanem odaadó tanár is, aki tanítványaiért mindent megtesz. Geőcze csakugyan beküldte Schlesingernek igen rövidre fogott francia nyelvű cikkét ‐ holott akkor még nem tudott franciául. Pár nap múlva megjött Schlesinger válasza, hogy a munka franciasága teljesen érthetetlen, írja meg cikkét magyarul, ha jó, gondja lesz rá. Csakugyan nem egész három hét múlva már Párizsból kapta meg a Francia Akadémia folyóiratában megjelent cikkének különlenyomatait. Előkelő nemesi neve ekkor megtette hatását, állami ösztöndíjjal kiküldték Párizsba, ahol éveket töltött.
Akkor ‐ és előtte és utána évtizedekig ‐ Göttingen és Párizs volt a matematikus világ két központja. Párizsban Geőcze meglepetéssel látta, hogy ott is volt matematikus, aki az ő problémájával foglalkozott. Ez az egyetem vele egyidős fiatal tanára, Henri Lebesgue (ejtsd: Löbeg) volt, századunknak egyik legnagyobb hatású matematikusa. (Ma talán a magyar és a szovjet matematikára gyakorolt hatása a legerősebb.)
Akkor persze Lebesgue még nem volt az a világhíresség, mint utóbb, de már sok nagy felfedezés állt mögötte. (Egyébként Lebesgue is évekig volt középiskolai tanár.) Geőcze tehát igen jó helyre került. Nem sokkal hazatérte után Budapestre helyezték át az V. kerületi Markó-utcai állami főreáliskolához. Budapesti tanársága idején kérte őt fel a minden iránt érdeklődő

≫

poeta doctus

≪

Babits Mihály (akkor még a budapesti X. ker. tisztviselőtelepi áll. főgimn. tanára), hogy vezesse őt be a matematikába. Geőcze erre nem azt az utat választotta, amit a legtöbb matematikus választott volna, nem a differenciál- és integrálszámítást, tehát nem a végtelen kicsi matematikáját adta elő, hanem a

≫

királyi utat

≪

, a halmazelméletet, a matematika egész új ágát, a végtelen nagy matematikáját. Ezzel eltalálta a filozofikus beállítottságú költő érdeklődését, aki nagy lelkesedéssel követte Geőcze előadását és a halmazelméletben nagy előhaladást tett.
Az egyetem továbbra is zárva maradt előtte, bármilyen nagytudású, nagy jelentőségű, sőt már nemzetközileg elismert matematikus volt ‐ hiába, nem volt doktori elme. Mikor végül a legelőkelőbb párizsi egyetemen, a Sorbonne-on (ejtsd: szorbon) megszerezte a doktorátust, az összes illetékes tényezők legnagyobb jóakarata ellenére, még három évig kellett várnia, amíg egyetemi magántanár lehetett. Így tehát csak egyetlen féléven át adott elő az egyetemen.
1914-ben ugyanis, a háború kitörésekor be kellett vonulnia és részt vett a szerbiai hadjáratban. Az 1914. decemberi visszavonulásban súlyos betegséget szerzett. 1915 februárban Versecen, ahol mindketten katonáskodtunk, meglátogatott. Szomorú emlék maradt számomra az a délután, melyet az a hatalmas termetű, bikaerejű ember fáradtan, betegen a pamlagon fekve töltött el. Amikor befolyásos rokonságának közbelépésére végül hazajöhetett, már késő volt, a harctéren szerzett betegségébe 1916. novemberében belehalt. Súlyos betegsége alatt sem hagyta abba matematikai vizsgálatait. A Magyar Tudományos Akadémián bemutatott egyik dolgozata csak két évvel halála után jelent meg.
Geőcze munkássága mélysége és eredetisége ellenére sem érte el mindjárt azt a sikert és megbecsülést, amelyet megérdemelt. Ennek részben maga Geőcze az oka, részben talán a kis nemzetek fiainak általános tragikuma. A matematikai dolgozattól is megkívánjuk ugyanis, hogy élvezetes stílusban jól legyen írva. A kis nemzetbeli tudós idegen nyelven kénytelen írni, amelyen általában kevésbé pontosan tudja magát kifejezni, mint anyanyelvén, ami persze a stílus élénkségének rovására megy, Geőcze pedig magyarul is rosszul fogalmazott. Dolgozatainak tárgya amúgy is igen nehéz, munkái tehát már nagy nehézségük miatt sem voltak élvezetes olvasmányok, ami népszerűségüket igen gátolta. Riesz Frigyesé, a mai magyar matematikai élet egyik legkiemelkedőbb tudósáé az érdem, hogy ma Geőcze mégis világszerte elismert matematikus. Riesz Frigyes még mint szegedi egyetemi tanár figyelmeztette Radó Tibort, aki akkor a szegedi egyetem fiatal magántanára volt (a 30-as évek elején, mint több más tudós is, külföldre távozott), erre a kincsesbányára. Radónak sikerült Geőcze eredményeit oly formában tárni a matematikus közönség elé, sőt ki is bővíteni, amellyel felkeltette irántuk az általános érdeklődést. Így vált Geőcze a magyar matematika egyik büszkeségévé!