Cím: Az 1953. évi Arany Dániel matematikai tanulóverseny (2. közl.)
Füzet: 1953/október, 33 - 41. oldal  PDF  |  MathML 
Témakör(ök): Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Alábbiakban közöljük a kitűzött feladatok megoldásait.

 

Az I. forduló feladatai
 

1. feladat: Számítsuk ki (x+y+z)2 értékét, ha
2x(y+z)=1+yz,1x-2y=23ésx+y+1z=0.

I. megoldás: A változók egyike sem lehet 0, így a törtek eltávolíthatók és a következő egyenletrendszert kapjuk:
2xy+2xz-yz=1,3xy+2xz-yz=0,xz+yz=-1.

Ez elsőfokú egyenletrendszer, ha xy, xz, yz-t tekintjük ismeretlennek. A második egyenletet levonva az elsőből, majd az egymásutáni egyenleteket 3, -2, 1-gyel, végül pedig 3, -2, -2-vel szorozva és összeadva kapjuk sorra, hogy
xy=-1,xz=23,yz=-53.
Innen
x2=xy⋅xzyz=25y2=xy⋅xyxz=52,z2=xz⋅yzxy=109.
Ezeket felhasználva
(x+y+z)2=x2+y2+z2+2(xy+xz+yz)==25+52+109+2(-1+23-53)=190.



II. megoldás: A harmadik egyenletből x+y értékét behelyettesítve
(x+y+z)2=(z-1z)2=z2+1z2-2,
így elég z2 értékét meghatároznunk. Az egyenleteknek az előző megoldásban szereplő alakját használva adjuk, össze az első és utolsó egyenletet:
2xy+3xz=0,y=-32z.

Ezt a második egyenletbe helyettesítve
-92xz+2xz+32z2=0,innenx=35z.

A nyert értékeket az első egyenletbe helyettesítve
-95z2+65z2+32z2=1,z2=109,
tehát
(x+y+z)2=109+910-2=190.

2.feladat: Melyik az a legkisebb 4-gyel végződő természetes szám, melynek utolsó jegyét a szám elé írva, az eredeti szám négyszereset kapjuk ?
 

I. megoldás: Jelöljük a keresett szám ismeretlen számjegyeit x1,x2,...,xn-nel. Ekkor a feladat olyan szám keresését kívánja, melyre
4⋅x1x2...xn4=4x1x2...xn.

Itt az egymásutáni betűk egy szám 10-es számrendszerbeli alakjának számjegyeit jelentik, a szorzás jelét mindig kiírjuk. A baloldal utolsó jegyét beszorozva 4-gyel (4⋅4=16) adódik, hogy xn=6; ezt a baloldalon beírva folytathatjuk a szorzást és kapjuk, hogy 4⋅6=24, 24+1=25 és így xn-1=5. Hasonlóan folytatva tovább sorra a 2, 0, 1 jegyeket kapjuk. Utóbbit 4-gyel szorozva 4-et kapunk, és nem marad továbbviendő egység, így kapjuk, hogy
4⋅102564=410256.

Nem kell az eljárást a 4-es jegynél befejezni, ekkor olyan számokhoz jutunk, melyek az 102 564 számjegysorozat többszöri megismétlésével keletkeznek. Ezek mind rendelkeznek a kívánt tulajdonsággal és az eljárásból belátható, hogy csak ezek a számok felelnek meg.
Lényegében ugyanígy adódik az eredmény akkor is, ha a jobboldali szám osztása révén határozzuk meg sorra a számjegyeket x1-től kezdve.
 

II. megoldás: Legyen a 4-es előtti jegyekből álló szám x és legyen n jegyű. Ekkor az adott szám 10x+4. A 4-es előre téve 4⋅10n-t fog jelenteni s ezt a számot követi az x szám. Így a feladat olyan x és n természetes számok keresését kívánja, amelyekre
4(10x+4)=4⋅10n+x,39x=4(10n-4).
A feladat tehát olyan n egész szám keresését kívánja, melyre 4(10n-4) osztható 39=3⋅13-mal. Mivel
10n-4=(10n-1)-3=99...9-3
osztható 3-mal, így csak a 13-mal való oszthatóságot kell biztosítani, és mivel 4 relatív prím a 13-hoz, így csak 10n-4 lehet 13-mal osztható. 10-4 és 102-4 nem osztható vele, tehát n>2. Ez esetben
10n-4=100⋅10n-2-4=4⋅(25⋅10n-2-1)=4[26⋅10n-2-(10n-2+1)].
Itt a 4 relatív prím a 13-hoz, 26 osztható vele, tehát a 10n-2+1-nek kell 13-mal oszthatónak lennie. Tudjuk, hogy 1001 osztható 13-mal, így n-2=3, n=5 a legkisebb kitevő, amelyik megfelel a feltételnek.
x=4⋅(105-4)39=10256,
a keresett szám tehát
102564.

Megjegyzés: 1. A 10m+1 kifejezés (n-2 helyett m-et írtunk) mindig osztható 13-mal, ha m a 3-nak páratlan többszöröse, mert ha m=3(2k+1), akkor
10m+1=(103)2k+1+1==(103+1)(103⋅2k-103(2k-1)+103(2k-2)+...-103+1)


és 103+1=7⋅11⋅13. Ha viszont m=3(2k+1)+r, r=1, 2, 3, 4 vagy 5, akkor
10m+1=(103(2k+1)+r+10r)-(10r-1)=10r(103(2k+1)+1)-(10r-1).

Itt az első tag osztható 13-mal, a második viszont nem, mert 9, 99=9⋅11, 999=9⋅111=9⋅3⋅37, 9999=9⋅1001+990 és 99999=99⋅1001+900; és itt egyik tényező sem osztható 13-mal, ill. az első tag osztható vele, a második azonban nem, tehát (m=n-2-t visszaírva) a felírt egyenlet összes megoldásai
x=4(106k+5-4)39,k=0,1,2....

Könnyen látható, hogy ezek éppen az előző megoldásban említett alakú számok.
2. Kérdés, nem csak véletlen-e, hagy találtunk a feltételnek megfelelő számot. Erre csak azt jegyezzük meg, hogy az utolsó feladatnak sincs mindig megoldása. Fermat egy nevezetes számelméleti tételéből, illetőleg annak Eulertől származó általánosításából következik, hogy olyan m kitevő minden a egész számhoz van, amelyre 10m-1 osztható a-val, ha a páratlan és nem osztható 5-tel; ezzel szemben 10m+1 pl. 3-mal nem lehet osztható, mert 10m+1=(10m-1)+2, ami 3-mal osztva 2-t ad maradékul, mert az első tag osztható 3-mal, bármilyen természetes szám is m.
 

3. feladat: Bizonyítandó, hogy trapézba akkor és csak akkor írható az oldalakat érintő kör, ha szárak, mint átmérők fölé írt körök érintkeznek.
 

I. megoldás: a) Tegyük fel, hogy a szárak fölé rajzolt körök érintkeznek. (1. ábra)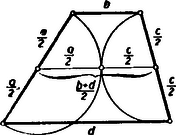
 
 
1. ábra
 

Ekkor a körök centrálisának hossza a sugarak összege, vagyis a szárak összegének a fele. Másrészt viszont a centrális éppen a trapéz középvonala, tehát hossza a párhuzamos oldalak összhosszának a fele. A feltételnek megfelelő trapézban tehát a szemközti oldalpárok összhossza megegyezik és tudjuk, hogy ha ez egy konvex négyszögre teljesül, akkor abba az oldalakat érintő kör írható. Tehát a feltétel elégséges.
b) Ha a trapézba az oldalakat érintő kör írható, akkor tudjuk, hogy a szemközti oldalpárok összege megegyezik s így a középvonal, melynek hossza a párhuzamos oldalak számtani közepe, egyben a szárak felének összegével is egyenlő s így a szárak mint átmérők fölé rajzolt körök közös pontban metszik a centrálist. De ha két körnek a centrálisukon van közös pontja, akkor e pontban érintkeznek. Tehát a feltétel szükséges is. Ezzel igazoltuk a bizonyítandó állítást.
 

II. megoldás: Tetszés szerinti ABCD trapéz (BC||AD) AB szára fölé rajzoljunk félkört. Messe ez a középvonalat E-ben (2. ábr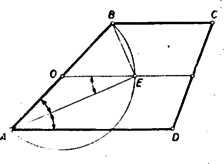a).
 
 
2. ábra
 

Ekkor E-n mennek át az A és B csúcsból húzott szögfelezők. Valóban, a félkör középpontját O-val jelölve AOE▵, egyenlő szárú s így OAE∢=OEA∢, mivel pedig a középvonal párhuzamos a párhuzamos oldalakkal, így OEA∢=EAD∢, tehát AE felezi az A-nál lévő szöget. Hasonlóan látható, hogy BE szögfelező.
A trapézba akkor és csakis akkor írható kör, ha a négy szögfelező egy ponton megy keresztül, tehát akkor és csakis akkor, ha a szárak fölé rajzolt köröknek közös pontja van a középvonalon, tehát ha e körök érintkeznek.
Egyben azt is nyertük, hogy a körök érintkezési pontja a beírt kör középpontját adja.
 

Megjegyzés. A versenyzők legnagyobb része csak a feladat egyik felét bizonyította be, mert nem volt tisztában azzal, hogy az >>akkor és csakis akkor<< azt jelenti, hogy be kell bizonyítani egyrészt, hogy a feltétel elégséges (>>akkor<<) és másrészt, hogy a feltétel egyszersmind szükséges is (>>csakis akkor<<), vagyis azt, hogy a tétel megfordítható. Hogy ez nincs mindig így ‐ tehát bizonyításra szorul ‐ ezt a következő két igen egyszerű példa világítja meg. >>Ha egy szám 5-re végződik, akkor osztható 5-tel. Itt az >>akkor<< nem toldható meg >>csakis akkor<<-ral, mert az 5-re végződés elégséges feltétel ugyan, de nem szükséges, hiszen a 0-ra végződő számok is oszthatók 5-tel. Viszont a következű állításban: >>Egy szám csakis akkor osztható 6-tal, ha páros<<, nem írhatunk a >>csakis akkor<< elé >>akkor<<-t, mert a szám páros volta ugyan szükséges feltétel, de nem elégséges, mert hiszen sok páros szám nem osztható 6-tal. Tehát a fenti két állítás egyike sem fordítható meg. (Ugyanis nem mondhatjuk: >>Az 5-re, végződő számok oszthatók 5-tel és fordítva, ha egy-egy szám osztható 5-tel, akkor 5-re végződik.<< Hasonlóképpen hamis: >>Minden 6-tal osztható szám páros és fordítva, minden páros szám osztható 6-tal.<<)
 

A II. forduló feladatai
 

1. feladat: Meghatározandó az x, y, z, u, v számjegyek értéke úgy, hogy a tízes számrendszerben felírt x61y064zuv szám osztható legyen 61875-tel.
 

I. megoldás: Bontsuk törzstényezőkre az osztót:
61875=32⋅54⋅11=9⋅11⋅625.

Mivel itt az egyes tényezők páronként relatív primek, azért ahhoz, hogy a keresett szám e szorzattal osztható legyen szükséges és egyben elegendő is, hogy az egyes tényezők külön maradék nélkül meg legyenek benne.
625-tel azok és csak azok a számok oszthatók, amelyeknek utolsó 4 jegyéből álló szám is osztható 625-tel. (L. >>K. M. L.<< 1953. márciusi számában a 88. oldalon a 70. sz. gyakorlatot.) 625-nek 4000 és 4999 közt csak egy többszöröse van:
7⋅625=4375,tehát4zuv=4375.

9-cel osztva minden szám ugyanazt a maradékot adja, mint a számjegyeinek összege, tehát kell, hogy
x+6+1+y+0+6+4+3+7+5=x+y+32=9m.

11-gyel osztva minden szám ugyanannyi maradékot ad, mint az a szám, amelyet kapunk, ha az egyesektől kezdve, minden második számjegyet összeadunk és ebből az összegből levonjuk a kihagyott számjegyek összegét (L. >>K. M. L.<< 1953. márciusi számában a 81. oldalon a 475. sz. feladatot.) Jelen esetben
(5+3+6+y+6)-(7+4+0+1+x)=(20+y)-(12+x)==8+y-x=11n.


Tehát
x+y=9m-32és-x+y=11n-8.
Itt x és y egyjegyű számok, tehát
0≤x+y≤18,-9≤-x+y≤9,
és így m=4 vagy 5, n=0 vagy 1. Mivel pedig két egész szám összege és különbsége közül nem lehet az egyik páratlan, a másik páros, így m=4, n=0 vagy m=5, n=1 felelhet meg. Első esetben y-ra negatív szám adódnék, tehát csak x+y=13 és -x+y=3 lehetséges, ahonnan x=5 és y=8.
A keresett szám tehát
5618064375,
és ennek valóban oszthatónak kell lennie 61 875-tel, mert az utolsó 3 jegy választása folytán osztható 625-tel, x és y megválasztása folytán pedig osztható 9-cel és 11-gyel.
 

II. megoldás: Ha a szám osztható 61 875-tel, akkor pl. a 16-szorosa osztható 16⋅61875=990000-rel, tehát minden esetre négy 0-val végződik. A kérdéses szám utolsó négy számjegye 4⋅16=64 folytán megegyezik a
4000+16⋅zuv
szánt utolsó négy jegyével. Mivel 16⋅zuv<16000, tehát csak úgy kaphatunk négy 0-ra végződő számot, ha
16⋅zuv=6000,vagyiszuv=375.
A keresett szám 16-szorosának ezenkívül még 99-cel kell oszthatónak lennie. Mivel 16 és 99 relatív primek, ez csak akkor következik be, ha az eredeti szám is osztható 99-cel. 99-re viszont egyszerű oszthatósági szabály található. (L. >>K. M. L.<< 1953. áprilisi számában a 118. oldalon a 74. sz. gyakorlatot.) Mivel
100=99+1,10000=99⋅101+1,1000000=99⋅10101+1,100000000=99⋅1010101+1,...


ezért a keresett szám ugyanannyi maradékot ad 99-cel osztva, mint a következő kétjegyű számok összege:
x6+1y+06+43+75=xy+140.
Ez a szám 140-nél nagyobb, 240-nél kisebb, tehát csak úgy lehet 99-cel osztható, ha 2⋅99=198-cal egyenlő, mely esetben
xy=58,tehátx=5,y=8,
és így a keresett szám
5618064375,
és ez valóban osztható 61 875-tel, mert osztható 99-cel, tehát a 16-szorosa is osztható vele, és a 16-szorosa ezenkívül négy 0-val végződik. Tehát 990 000-rel osztható a szám 16-szorosa és így az eredeti mindenesetre osztható ennek 16-odával, 61 875-tel.
 

2. feladat: Egy kör AB és CD átmérői merőlegesek egymásra, a CE húr párhuzamos a BF húrral, E ill. F tükörképei CD-re vonatkozóan H ill. G. Bizonyítandó, hogy az ABFG trapéz területe egyenlő CEH háromszög területével.
A leírás különböző ábrákhoz vezethet (1., 2. és 3. ábra), aszerint, hogy hol vesszük fel az E pontot. Az 1. ábrán a BD a 2.-on DA negyedkörön vettük az E pontot. A két ábrán, csak a trapéz helyzete tükrös egymáshoz képest az AB átmérőre vonatkozóan. Ez a területekre nincs befolyással. Ha ellenben E átjut az AC ívre (3. ábra), akkor az ABFG négyszög hurkolt négyszög két párhuzamos oldallal: >>hurkolt trapéz<<.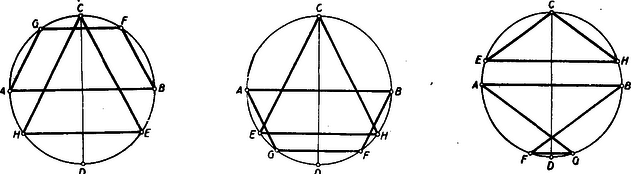
 
 
1. ábra    2. ábra    3. ábra
 

Az állítás erre az esetre is igaz, ha a hurkolt trapéz területét megfelelően értelmezzük, de hogy egyáltalán mit értsünk egy önmagát metsző négyszög területén, az eleve nem világos és ezért hibáztatható is a feladat megfogalmazása.
Az ABGF trapéz területét venni, vagy akár a két háromszög területének összegét, ez a feladat szempontjából nem megfelelő, hiszen a keletkezett kettős háromszögből az AB oldalhoz csatlakozó hasonló a CEH háromszöghöz, de már egymagában is nagyobb nála, mert AB>EH. Hogy a terület milyen értelmezése mellett érvényes az állítás ebben az esetben is, az bizonyítás közben fog adódni. Ha E a CB ívre kerül, akkor lényegesen új esetet nem kapunk, csak a >>hurkolt trapéz<< kerül ismét az AB átmérő másik partjára. Térjünk ezután a feladat megoldására.
 

I. megoldás: Alakítsuk először a trapézt téglalappá úgy, hogy az F-ből AB-re bocsátott FK merőlegessel elvágott BFK háromszöget a GA oldalhoz illesztjük (4. ábra).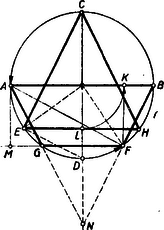
 
 
4. ábra
 

Az így keletkezett AMFK téglalapot az AF átlóval két egyenlő részre osztjuk, és megmutatjuk, hogy a keletkezett AFK▵ egybevágó a CEH háromszög felét kitevő CEL háromszöggel, ahol L az EH húr középpontja (mely nyilván CD-re esik). Valóban forgassuk el utóbbit a kör középpontja körül az óra járásával ellenkező irányban 90∘-kal. Ekkor C átmegy A-ba és mivel D az elforgatás után B-be kerül, így L az AB átmérőre fog kerülni. Azt kell csak belátnunk, hogy az E pont F-be megy át, ez pedig teljesül, mert a BC és EF ívet párhuzamos húrok metszik ki a körből, tehát az EF ív is negyedkör.
A bizonyítás lényegtelen változtatással alkalmazható arra az esetre is, ha E a BD negyedkörön van (a következő megoldásból látható lesz, hogy hogyan), nem világos azonban, hogy hogyan vihető át a hurkolt esetre. Ez sokkal könnyebben lesz látható a következő megoldásból, amely szoros rokonságban van az elsővel.
 

II. megoldás: Az előbbi jelöléseket használva (4. ábra) nyilvánvaló, hogy AK a trapéz középvonalával egyenlő, tehát a trapéz ill. háromszög t1 ill. t2 területe
t1=AK⋅FK,t2=CL⋅EH2=CL⋅EL.
Megmutatjuk, hogy
FK=ELésAK=CL,
ill. utóbbi helyett, hogy BK=DL. Mindkét egyenlőség következik abból, hogy
BFK▵≅DEL▵.

Forgassuk el az utóbbi háromszöget 90∘-kal az óra járásával ellenkező irányban a kör középpontja körül. Ekkor D átmegy B-be, EL pedig a B-hez húzott sugárra merőleges helyzetbe kerül, E pedig átmegy F-be, amint azt az I. megoldásban láttuk. Ezzel állításunkat igazoltuk.
 

Megjegyzés: A bizonyítás >>hurkolt trapéz<< (5. ábra) esetén is azt adja, hogy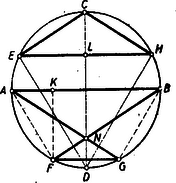
EL=FK,DL=BK,amibőlCL=AK,
tehát
EL⋅CL=FK⋅AK=FK.AB-FG2=FK⋅AB2-FK⋅FG2.
 
5. ábra
 

Baloldalt ismét a CEH▵ területe áll, a jobboldal viszont felfogható az AFB és AFG háromszögek területei különbségének. Ebből a különbségből kiesik a két háromszög közös részének a területe és marad a >>hurkolt trapéz<< nagyobb és kisebb háromszöge területének különbsége. A hurkolt esetben tehát e területkülönbség egyezik meg a CEH háromszög területével.
Számítás nélkül is bebizonyíthatjuk ezt az eredményt. Ugyanis a közönséges trapézra fentebb már bebizonyított tétel alapján az 5. ábrában a DEH▵ területe egyenlő az ABGF közönséges trapéz területével, továbbá ugyancsak az előbbiek alapján ABF▵≅CDE▵≅CDH▵≅BGA▵.
Tehát (területekről beszélve)
CEH=CEDH-DEH=CEDH-ABGF==CEDH-(ABF+ABG-ABN+FGN)==CDE+CDH-ABF-ABG+ABN-FGN=ABN-FGN.



Könnyű a feladatot úgy fogalmazni, hogy a kettősség ne is lépjen fel. (L. 4. és 5. ábrát). Ha a BF és AG egyenesek metszéspontját mindenkor N-el jelöljük, akkor a CEH háromszög területe ‐ minden esetben ‐ az ABN és GFN háromszögek területének különbségével egyenlő.
A III. osztályosok más szempontból is érthetőnek fogják tartani a nyert eredményt. A koordináta-geometriában ugyanis kiderült, bizonyos szempontból előnyös lehet a területet előjeles mennyiségnek tekinteni, oly módon, hogy minden idomhoz megadjuk, hogy hogyan járjuk körül a kerületét (sokszögeknél ez például a csúcsok sorrendjével már meg van adva) és akkor azon idomok területét, melyek körüljárásban a jobbkezünk felé esnek, ellenkező előjelűnek nevezzük, mint amelyek körüljáráskor balról fekszenek. (Bármelyik lehet pozitív, de a másik minden esetben negatív lesz.) Ilyen értelmezés mellett hurkolt négyszög területéül mindig azon két háromszög területének különbsége adódik, melyekből a hurkolt négyszög áll.
 

III. megoldás: Mivel mindkét szóban forgó idom tükrös a CD átmérőre, mint tengelyre, így elég azt megmutatni, hogy a háromszög fele és a trapéz fele egyenlő területű, tehát ha az FG és EH húrok felezőpontjai J és L (6. ábra), akkor azt kell megmutatnunk, hogy a CEL háromszög és a BFJO trapéz egyenlő területű.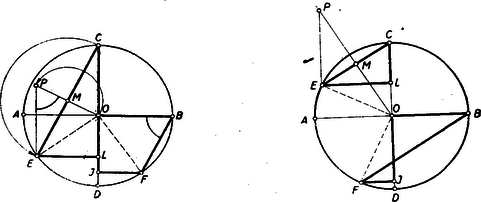
 
 
6. ábra           7. ábra
 

Húzzuk meg az EC húr OM felező merőlegesét és forgassuk a CMO háromszöget az M pont körül az EM szakasz mellé. Az így keletkezett ELOP derékszögű trapézban
EPO∢=OBF∢
mint merőlegesszárú szögek, mert PO merőleges a CE-vel párhuzamos BF húrra is. EP és OB, a trapézok hosszabb párhuzamos oldalai sugárnyi hosszúságúak és ugyancsak sugárnyi hosszúságú az EO ill. OF átló is. Így a BFJO trapéz egybevágó, tehát egyenlő területű is, a POLE trapézzal, tehát egyenlő területű a CEL háromszöggel is.
A hurkolt esetben is igaz, hogy az CEO háromszög átalakítható a PEO háromszöggé (7. ábra) és utóbbi egybevágó a BOF háromszöggel. Viszont előbbiből most el kell hagyni az ELO háromszöget, hogy a CEL háromszöget kapjuk. Ennek megfelelően BFO-ból OJF-fel egyenlő területet kell elvennünk. A közös rész elhagyása után a hurkolt négyszög OB-hez csatlakozó nagyobb háromszöge marad meg. Ebből kell még az FJ-hez csatlakozó kisebb háromszöget elvenni, hogy CEL-lel egyenlő területet kapjunk.
 

3. feladat: Bizonyítsuk be, hogy ha
1a+1b+1c=1a+b+c,
és n pozitív páratlan szám, akkor
1an+1bn+1cn=1an+bn+cn.

I. megoldás: Vigyük át az első egyenlet baloldaláról az utolsó tagot a jobboldalra:
1a+1b=1a+b+c-1c,a+bab=-(a+b)c(a+b+c).
Redukáljuk az egyenletet 0-ra és emeljük ki (a+b)-t:
(a+b)(1ab+1c(a+b+c))=(a+b)[ab+(a+b)c+c2]abc(a+b+c)==(a+b)(a+c)(b+c)abc(a+b+c)=0.


Ez csak úgy lehet 0, ha a számláló 0. Teljesen hasonlóan a második egyenlet
(an+bn)(bn+cn)(cn+an)anbncn(an+bn+cn)=0
alakba írható. Mivel páratlan pozitív egész n-re
un+vn=(u+v)(un-1-un-2v+...-uvn-2+vn-1),
azért a számláló osztható az
(a+b)(b+c)(c+a)
szorzattal, így a második egyenlőség is teljesül, ha az első teljesül.
 

II. megoldás: Az első egyenletet átalakítva
ab+bc+caabc=1a+b+c,vagyis(a+b+c)(ab+bc+ca)=abc.
Írjunk fel egy olyan egyenletet, melynek gyökei a, b és c:
0=(x-a)(x-b)(x-c)=x3-(a+b+c)x2+(ab+bc+ca)x-abc==x3-(a+b+c)x2+(ab+bc+ca)x-(a+b+c)(ab+bc+ca)==x2[x-(a+b+c)]+(ab+bc+ca)[x-(a+b+c)]==[x-(a+b+c)][x2+(ab+bc+ca)].



Az első alakról látható, hogy ez csak akkor teljesülhet, ha x megegyezik a b, c valamelyikével, az utolsóból viszont következik, hogy a kifejezés eltűnik, ha x=a+b+c, tehát utóbbinak meg kell egyeznie az előbbiek valamelyikével pl.
a+b+c=a,c=-b,
s így páratlan egész n-re
1an+1bn+1cn=1an+1bn-1bn=1an=1an+bn+(-b)n=1an+bn+cn
is teljesül.