Cím: Az 1953. évi Rákosi Mátyás matematikai tanulmányi verseny II. (döntő) fordulója
Füzet: 1953/szeptember, 1 - 7. oldal  PDF  |  MathML 
Témakör(ök): OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A II. (döntő) fordulóban, amely április 12-én folyt le, 90 iskola 186 tanulója (79 gimn. 162 tan. ‐ 11 ip. techn. 24 tan.) indult. Öt óra munkaidő állott rendelkezésre az alábbi három feladat megoldására:
1. Néhány adat a szovjet ipar termelésének emelkedéséről (az 1940. évihez viszonyítva):

1940    1950    1951    1952  Termelési eszközök . . . . .  100205239267  Fogyasztási  cikkek . . . . .  100143  Együtt . . . .  100173202224  (1)
fogyasztási cikkek 1952. évi termelése hány százaléka volt az 1950. évinek?
2. Egy 60∘-os szög egyik szárán elhelyezkedő A, ill. A1 pontnak a szög csúcsától való távolsága p, ill. 2q; a másik száron elhelyezkedő B, ill. B1 pontnak a csúcsától való távolsága pedig q, ill. 2p. Az A1B1 távolság felezőpontja C. Bizonyítandó, hogy az ABC háromszög szabályos.
3. Mi az utolsó értékes jegye az első száz természetes szám szorzatának?
A bírálóbizottság április 27-én a következő jelentést fogadta el:
>>A Bizottság örvendetes javulást lát a döntő dolgozatai átlagos értékében és a feladatmegoldások megszövegezésében; sajnálattal állapítja azonban meg, hogy egy különösebb nehézséget nem rejtő százalékszámítási feladat sok versenyzőnek okozott indokolatlanul nagy nehézséget. Igen sajnálatos az is, hogy a legjobb dolgozatokban is gyakori a hibás osztás, sőt összeadás és kivonás is. Ezek a számítási hibák sok versenyző eredményét rontották lényegesen. Ugyancsak sajnálatos a lányok gyenge szereplése.
Mindhárom feladatot lényegében megoldotta 16 versenyző, további 17 versenyző dolgozata két feladat megoldása mellett mutat fel értékes próbálkozást a harmadik feladat megoldásában is, vagy a két feladat közül valamelyiket ötletesen, vagy több úton tárgyalja. Újabb 37 dolgozat tartalmazza két feladat lényegében jó megoldását.
Az első csoport dolgozatai közül is kiemelkedik Kántor Sándor dolgozata, aki hibátlanul oldja meg mindhárom feladatot. A második feladatra három különböző elemi megoldást ad, megemlíti egy egyszerűbb általánosítás lehetőségét és egy trigonometriai számítással is igazolja az állítást. A harmadik feladatot a tényezők alkalmas, ha nem is a legegyszerűbb csoportosításával oldja meg. A Bizottság javasolja, hagy az I. díjat Kántor Sándor-nak ítéljék oda.
A további 15 dolgozat között nem túl nagyok az értékbeli különbségek, mégis elválik a többitől három dolgozat. Ezek szerzői Surányi Péter, Szilárd Miklós és Tomor Benedek. Surányi hibátlanul oldja meg mindhárom feladatot, bár a másodikra csak számításon alapuló megoldást ad, viszont rámutat a Kántor áltat is felvetett általánosítási lehetőségre. A harmadik feladatot megoldja a tényezők csoportosításával és a szorzat törzstényezőkre bontásával is. Szilárd a második feladatra rövid, világosan fogalmazott szellemes elemi megoldást ad. Lényegében jól oldja meg a másik két feladatot is, de mindkettőben kisebb számolási hibát vét. A harmadik feladatban törzstényezőkre bontás után ügyesen csoportosítja a tényezőket. Tomor Szilárdéhoz hasonló szellemes elemi megoldást talál a második feladatra, a harmadik feladatot is jól oldja meg törzstényezőkre bontással, az elsőben fölösleges számításokba bocsátkozik, amikben hibáz is.
A Bizottság javasolja, hogy a második díjat Surányi Péter, Szilárd Miklós és Tomor Benedek közt osszák meg. Az első csoportba tartozó további 12 dolgozat szerzőit első dicséretbe, a második csoport 17 dolgozatának szerzőit második dicséretre, a harmadik csoport 37 dolgozatának szerzőit pedig harmadik dicséretre javasolja a Bizottság<<.
A K. M. a bírálóbizottság javaslata alapján a következő döntést hozta:
1. díj (oklevél és 1000 Ft pénzjutalom):
Kántor Sándor (Debrecen, Ref. Koll. g. IV. o. t.).
2. díj (oklevél és 500 Ft pénzjutalom):
Surányi Péter (Bp. VI., Kölcsey Ferenc g. IV. o. t.);
Szilárd Miklós (Balassagyarmat, Balassa Bálint g. IV. o. t.);
Tomor Benedek (Győr, Révai Miklós g. III. o. t.).
 

I. dicséretben és nagyobb könyvjulalomban részesült:
 
Balatoni Ferenc (Bp. III., Árpád g. III. o. t.),
Beretvás Tamás (Bp. XIII., Berzsenyi g. IV. o. t.),
Grátzer György (Bp. VI., Kölcsey g. III. o. t.),
Jókai Zoltán (Bp. VIII., 7. sz. gépip. techn. IV. o. t.),
Keresztély Sándor (Miskolc, Földes Ferenc g. IV. o. t.),
Kovács László (Debrecen, Ref. g. III. o. t.),
Kroó Norbert (Bp., IX., Fáy g. IV. o. t.),
Schmidt Eligius (Bp. I., Fürst Sándor g. III. o. t.),
Siklósi Péter (Sopron, Széchenyi g. III. o. t.),
Vigassy József (Bp. I., Petőfi g. III. o. t.),
Zawadowski Alfréd (Bp. I., Petőfi g. III. o. t.),
Zobor Ervin (Nagykanizsa, Irányi Dániel g. IV. o. t.).
 

II. dícséretet és könvjutalmat nyert:
 
Bánki György (Bp., XI., József Attila g. IV. o. t.), Csáki Endre (Győr, Révai Miklós g. IV. o. t.), Dömölki Bálint (Bp., XXI., Jedlik Ányos g. IV. o. t.), Frajka Zoltán (Karcag, Gábor Áron g. IV. o. t.), Kardos Péter (Szolnok, 16. sz. gépipari techn. III. o. t.), Németh Lehel (Jászberény, Mikszáth g. III. o. t.), Papp Zoltán (Sárospatak, Rákóczi g. III. o. t.), Reichlin-M. Viktor (Bp., V., Piarista g. III. o. t.), Rédly Elemér (Pannonhalma, Bencés g. IV. o. t.), Rippel Géza (Bp., VIII., Vörösmarty g. III. o. t.), Rockenbauer Magda (Bp., X., I. László g. IV. o. t.), Sélley Gábor (Bp., X., I. László g. III. o. t.), Sóti Ferenc (Szeged, 5. sz. vegyip. techn. IV. o. t.), Szabó Dániel (Esztergom, I. István g. IV. o. t.), Szabó József (Szolnok, Beloiannisz g. IV. o. t.), Tilesch Ferenc (Esztergom, I. István g. IV. o. t.), Zádor Pál (Bp., VI., Kölcsey g. IV. o t.).
 

III. dícséretben és könyvjutalomban részesült:
 
Alexander Gábor (Bp., XIV., I. István g. III. o. t.), Babos Károly (Székesfehérvár, József Attila g. III. o. t.), Bagi András (Bp., IX., Apáczai Csere János g. III. o. t.), Bársony András (Nagykanizsa, Irányi Dániel g. IV. o. t.), Bódás Péter (Székesfehérvár, József Attila g. III. o. t.), Burger Péter (Bp., VII., Madách g. III. o. t.), Csanády Mihály (Esztergom, I. István g. III. o. t.), Csonka Pál (Bp., XI., József Attila g.), Deseő Zoltán (Bp., X., I. László g. III. o. t.), Dinnyés József (Szeged, 17. sz, gépipari techn. IV. o. t.), Ehrenfeld János (Bp., VIII., 3. sz. gépip. techn. III. o. t.), Erdélyi Miklós (Oleg Kosevoj Ösztöndíjas isk.), Fuhrmann Róbert (Bp., VIII., Fazekas g. IV. o. t.), Gaál István (Csorna, Latinka Sándor g. III. o. t.), Gyapjas Ferenc (Bp., VIII., Széchenyi g. IV. o. t.), Habermayer István (Bp., VIII., 7. sz. gépipari techn. III. o. t.), Hettyei Gábor (Orosháza, Táncsics g. IV. o. t.), Horváth Jenő (Celldömölk, Gábor Áron g. IV. o. t.), Huszár Károly (Bp. II., Rákóczi g. III. o. t.), Jámbor Imre (Zalaegerszeg, Zrínyi Miklós g. III. o. t.), Klafszky Emil (Győr, Révai g. IV. o. t.), Krén Emil (Bp., V., I. sz. textilip. techn. IV. o. t.), Leitold Ferenc (Győr, Révai g. IV. o. t.), Magyary-Kossa Miklós (Esztergom, I. István g. IV. o. t.), Marik Miklós (Bp., I., Fürst Sándor g. III. o. t.), Marti Sándor (Szeged, Radnóti g. IV. o. t.), Molnár István (Debrecen, Ref. g. III. o. t.), Pergel József (Bp., XIX., Landler Jenő g. IV. o. t.), Polgár Iván (Szeged, 5. sz. vegyipari techn. IV. o. t.), Radda György (Pannonhalma, Bencés g. III. o. t.), Rácz Márton (Bp., II., Rákóczi g. III. o. t.), Rozsondai Béla (Sopron, Széchenyi g. IV. o. t.), Száz Kálmán (Veszprém, Lovassy László g. IV. o. t.), Szilárd Katalin (Bp., XIII., Berzsenyi g. IV. o. t.), Telkes Zoltán (Aszód, Petőfi g. IV. o. t.), Theisz Péter (Kaposvár, Táncsics g. IV. o. t.), Venetiáner Pál (Bp., VI., Kölcsey g. IV. o. t.).
Ezek szerint tehát 46 iskola 70 tanulója (40 gimn. 62 tan.‐ 6. i. techn. 8 tan.) részesült kitüntetésben. Örömmel állapítjuk meg, hogy a helyezést elért 70 tanuló közül 52-en (74%) voltak lapunk feladatmegoldói. (Részletes beszámoló ‐ sokféle szempontból ‐ a >>Köznevelés<< június 1-én megjelent 11. számában, a 267‐8. oldalon található.)
Alább közöljük a II. forduló feladatainak megoldását:
 


1. feladat.
 
A feladat általában indokolatlanul nagy nehézséget okozott a versenyzőknek. A számolási hibákra a jelentés is rámutatott, de ezen túlmenően, ahhoz képest, hogy az utolsó évfolyamok legjobb diákjairól volt szó, túlságosan sokan voltak; akik még jó esetben a két termelés számtani közepéből számolták a hiányzó adatokat, vagy ennél is hibásabban számoltak, ha egyáltalán megpróbálkoztak ezzel a feladattal, amit különösebb fejtörés nélkül kellett volna tudniok megoldani.
 
Megoldás: Viszonyítsunk mindent a fogyasztási cikkek 1940. évi termeléséhez. Ha ennek p-szerese volt az eszközök ugyanazon évi termelése, akkor p a következőképpen számítható ki az 1951. évi adatokból. Az alapul vett értékeknek az 1951. évi fogyasztási cikktermelés, adataink szerint, 143%-a, a termelő eszköz termelés pedig p⋅239%-a. Az össztermelés 1940-ben a fogyasztási cikk-termelés 1+p-szerese, így az 1951. évi össztermelés (1+p) 202%-a, tehát
143+239p=(1+p)202,  ahonnan  p=5937.

Ha a fogyasztási cikkek termelése az 1940. évinek 1950-ben x%-a, 1952-ben pedig y%-a, akkor a meghatározandó mennyiség 100yx. Az előbbi mintájára külön-külön is meghatározható x és y:
x+205p=(1+p)173,x=173-32p;y+267p=(1+p)224,y=224-43p.
Innen
100yx=100224⋅37-43⋅59173⋅37-32⋅59=5751004513=127,4.

A fogyasztási cikkek termelése tehát a Szovjetunióban 1950-től 1952-ig a 127%-ára nőtt. (A tizedesjegy megadása nem bírna értelemmel, mert a kiindulási értékek is csak egész %-okban vannak megadva, s így az eredmény tizedesjegyei már nem megbízhatók, legfeljebb kerekítés szempontjából lehet hasznos az első.)
 


2. feladat.
 

Ez okozta a legkevesebb nehézséget, bár sokan ágyúval lőttek verébre, amikor trigonometriai és koordinátás számításokat használtak ennek a tisztán I. osztályos anyagismerettel is megoldható feladatnak megoldásához. Itt csak néhányat mutatunk be a számos elemi megoldás közül. Jelöljük a szög csúcsát σ-val és tegyük fel mindig, hogy q≤p. Ezt szimmetria okokból megtehetjük az általánosság csorbítása nélkül. B tehát mindig O és B1 közt van.
 

I. megoldás: Az AOB▵ és B1OA1▵ hasonló, mert O-nál fekvő szögük közös, az ezt közrezáró oldalak pedig az utóbbi háromszögben kétszer akkorák, mint az előbbiben. Bocsássunk másrészt A1-ből merőlegest az OB szárra. Mivel az O-nál lévő szög 60∘, így e merőleges talppontja O-tól 12OA1=q távolságra van, vagyis B-vel azonos. Bocsássunk C-ből is merőlegest OB-re ennek talppontja legyen D. Mivel CD az A1B1B▵ középvonala, azért BD=DB1, vagyis a BCB1▵ egyenlőszárú. Ebből és a fenti hasonlóságból adódik, hogy az 1. ábrán egyformán jelzett szögek egyenlők. Mivel az A1-nél és B1-nél megjelölt szögek összege az O-nál lévő 60∘-os szöget 180∘-ra egészíti ki, azért 60∘-osnak kell lennie az 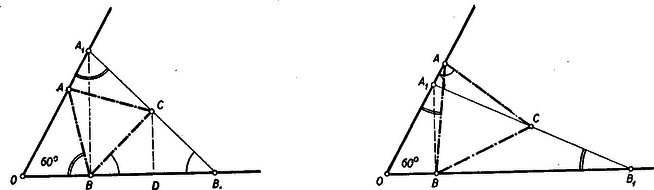ABC∢-nek is.
 
 
1. ábra          2. ábra
 

Ugyanúgy látható, hogy BAC∢=60∘, ha p≤2q, ha azonban 2q<p, akkor az A-nál megjelölt szög (2. ábra) az A1OB1▵ A1-nél lévő külső szögével egyenlő. Viszont ez esetben az egyíves és kétíves szög különbsége adja ki az O-nál lévő 60∘-ot s így egyszersmind BAC∢=60∘. Az ABC▵-nek tehát minden esetben A-nál és B-nél 60∘-os szöge van. Így harmadik szöge is 60∘-os. tehát a háromszög szabályos.
II. megoldás: Az előző megoldásban láttuk, hogy A1B⊥OB1. Hasonlóan következik, hogy B1A⊥OA. Így A és B az A1B1 fölötti Thales körön vannak, melynek középpontja C, tehát AC=BC (3. ábra). Az ACB∢ az AA1B∢=OA1B∢-höz, mint kerületi szöghöz, tartozó középponti szög. Mivel az előbbi szög az O-nál lévő 60∘-os szög pótszöge, azaz 30∘, azért a hozzátartozó középponti szög 60∘-os, tehát az egyenlő szárú ABC▵ egyik szöge 60∘, s így a háromszög szabályos.
Figyeljük meg, hogy a bizonyítás független p és q nagyság viszonyától. Ez állni fog a későbbi megoldásokra is.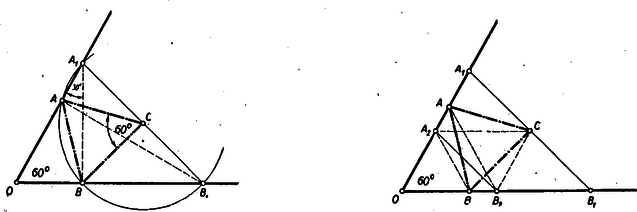
 
 
3. ábra          4. ábra
 

III. megoldás: Jelöljük OA1 ill. OB1 felezőpontját A2-vel ill. B2-vel. Megmutatjuk, hogy az ABC▵ minden oldala egyenlő az A2B2 távolsággal (4. ábra).
OA2=q=OB és OB2=p=OA, tehát OA2B▵ és OAB2▵ szabályosak. Így AA2BB2 egyenlőszárú trapéz, tehát átlói egyenlők: AB=A2B2.
Egyenlőszárú trapéz az A2BB2C négyszög is, mert A2C∥OB1 mint az A1OB1▵ középvonala; B2C e háromszög egy másik középvonala, tehát B2C=12OA1=q=A2B. Így ezen trapéz átlói is egyenlők: BC=A2B2.
Az AA2B2C négyszögről már tudjuk, hogy trapéz, mert B2C középvonal. Az OA2CB2 paralelogrammából és OAB2 szabályos háromszögből A2C=OB2=AB2, tehát a trapéz átlói egyenlők, így a trapéz egyenlő szárú, vagyis AC=A2B2. Az ABC háromszög tehát szabályos.
IV. megoldás: Ha p=q, a kérdéses pontokat jelöljük A∘, A1, B, B1∘, C∘-v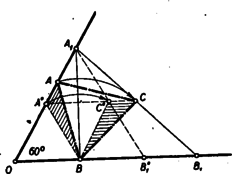al (5. ábra).
 
 
5. ábra
 

Ez esetben az A∘BC∘ háromszöget az OA1B1∘ szabályos háromszög oldalközéppontjai alkotják, tehát szintén szabályos. Növeljük most meg OA∘-t, akkor A∘ valamilyen A helyzetbe kerül, B1∘ egy olyan B1-be, melyre B1∘B1=2A∘A, C pedig az OB-vel párhuzamos A∘C∘ egyenes meghosszabbításán mozdul el és olyan C helyzetbe jut, melyre C∘C=12B1∘B1=A∘A, mert a baloldali távolság, az A1B1∘B1▵ középvonala. Forgassuk az AA∘B▵-et B körül az órajárásával megegyező irányba 60∘-kal. Ekkor A∘ átmegy C∘-ba A∘A iránya párhuzamossá válik OB1-ével s így az éppen megállapított távolságegyenlőségek folytán A éppen C-re kerül. AB és CB tehát 60∘-os elforgatással egymásba vihető, amiből következik, hogy az ABC háromszög szabályos.
Egyszerűbb bizonyításhoz jutunk, ha az egymásba forgatott háromszögekhez hozzácsatoljuk az egybevágó OA∘B ill. A∘BC∘ egybevágó háromszögeket (Ez annak felel meg, hogy az A pontot nem az A∘ helyzetből, hanem az O pontból elindulva mozdítjuk el a végső helyzetébe.)
 
V. megoldás: Legyen OA1 felezőpontja D (6. ábra). Ekkor DC az A1OB1▵ középvonala, így DC=12OB1=OA és DC∥OB1. Másrészt OD=12OA1=q=OB, tehát CDB∢=DBO∢=60∘. Forgassuk a BCD háromszöget B körül az óra járásával ellenkező irányba 60∘-kal. Ekkor D éppen O-ba kerül, C pedig a BO-val 60∘-ot bezáró egyenesre, tehát OA1-re, éppen az A pontba. Eszerint BC 60∘-os elforgatással BA-ba megy át, tehát az ABC háromszög szabályos.
 
 
6. ábra          7. ábra
 

Általánosítások: A tétel többféleképpen általánosítható. L. pl. a jelen számban kitűzött 147. sz. gyakorlatot. Egy másik általánosítás a következő: Legyen OA1B2 és A2B1O két szabályos háromszög, melyek O csúcspontja egybeesik és a megadott két körüljárás egyező irányú, akkor az OA2, B2O ill. A1B1 távolságok A, B ill. C felezőpontjai szabályos háromszöget alkotnak. (Versenytételünk ennek az általánosított feladatnak azon speciális esete, amelyben az O csúcsból kiinduló oldalak is egymásra kerülnek, amikor az A1 és B2 csúcsokat említenünk sem kell.)
Ezen állítás éppenúgy bizonyítható, mint az eredeti verseny feladat. Vegyük pl. az V. megoldás mintájára az OA1 szakasz D felezőpontját (7. ábra), akkor a BCD▵-et 60∘-kal elforgatva a D pont O-ba a DC szakasz pedig OA-ra kerül, tehát BC 60∘-os elforgatással átvihető BA-ba, s így az ABC háromszög szabályos.
Az állítás így minden esetre elég körülményesen hangzik, ezzel szemben messzemenően általánosítható. Nem lényeges benne sem a háromszögek szabályossága, csak a hasonlóságuk, sem a közös csúcspont, és a felezőpont is mással pótolható. Így pl. igaz az 554. sz. feladatban bizonyításra kitűzött tétel.
 


3. feladat.
 

Itt az egyetlen nehézséget az 5-tel osztható tényezők okozzák, amelyek alkalmas párral szorozva 0-végződésű számot adnak. Ha a szorzatot törzstényezőkre bontjuk, akkor ez a nehézség nem merül fel.
I. megoldás: Az első 100 szám közt 50 páros van, ezek közül 25 még 4-gyel is, azok közül 12 még 8-cal is 6 még 16-tal is, 3 még 32-vel is és 1 (maga a 64) 64-gyel is osztható. Így a szorzat 2-nek az (50+25+12+6+3+1=)97-ik hatványával osztható. Hasonlóan meghatározhatjuk a többi törzsszám kitevőjét is és kapjuk, hogy 1⋅2⋅3⋅...⋅99⋅100=287⋅348⋅524⋅716⋅119⋅137⋅175⋅195⋅234⋅293⋅313⋅372⋅412⋅432⋅472⋅53⋅59⋅61⋅67⋅71⋅73⋅79⋅83⋅89⋅97. Itt 5 hatványát a 2 ugyanannyiadik hatványával párosítva 1024-t kapunk, amivel szorozva az utolsó jegy nem változik, ezt a tényezőt tehát elhagyhatjuk. A további tényezőknek csak az utolsó számjegyével szorozva kapunk a szorzatban egyeseket, így a tízeseket az egyes tényezőkből szintén elhagyhatjuk és egészen elhagyhatjuk az 1-re végződő tényezőket. A kérdéses szorzatnak tehát ugyanaz az utolsó értékes jegye, mint a következő szorzaté:

273⋅348⋅716⋅37⋅75⋅95⋅34⋅93⋅72⋅32⋅72⋅3⋅9⋅7⋅3⋅9⋅3⋅9⋅7==273⋅386⋅727=1618⋅2⋅8121⋅32⋅(492)6⋅73.


6-ra végződő szám minden hatványa is 6-ra végződik. Ha pedig páros számot 6-tal szorzunk, akkor az utolsó jegy nem változik meg. Így az első két tényező szorzatának utolsó jegye 2. A harmadik tényező elhagyható és az ötödik is, mert 492 is 1-re végződik. 73 utolsó jegye 3 s így az első 100 természetes szám szorzata ugyanarra a jegyre végződik, mint 2⋅9⋅3, vagyis 4-re.
Nyilvánvaló; hogy itt csak a 2 és 5 törzstényezők szerepe volt lényeges, az is csak addig, míg leválasztottuk 10 legmagasabb hatványát, amivel a szorzat osztható, azután már egy egyes tényezők prím volta nem volt lényeges, hiszen egyeseket a 9, összetett számmal helyettesítettük. Így a törzstényezős felbontás fölösleges segédeszköznek látszik és valóban mellőzhető is, mint azt az alábbi II. megoldás mutatja.
 

II. megoldás: Válasszuk külön azon tényezőket, amelyek utolsó értékes jegye 2 vagy 5 (tehát a 20-at és 50-et is). 20⋅50=1000 nem befolyásolja a kérdéses szorzat utolsó jegyét, úgy szintén a kiválasztott páros tényezőkből leválasztva a 2 tényezőt, a páratlanokból az 5-öt és ezeket összeszorozva a keletkező 10-hatvány sem. A kiválasztott tényezők szorzata tehát
2⋅12⋅22⋅...⋅82⋅92⋅5⋅15⋅25⋅...⋅75⋅85⋅95⋅20⋅50==1⋅6⋅11⋅...⋅36⋅41⋅46⋅1⋅3⋅5⋅...⋅15⋅17⋅19⋅1013.

Visszamaradt tehát két 5-re végződő tényező, az 5 és 15. Szorozzuk ezeket össze a 36-tal:
5⋅15⋅36=5⋅5⋅3⋅9⋅4=2700

A többi kiválasztott tényezők közül az 1-gyel végződők elhagyhatók, a 6 végűek szorzata is 6-tal végződik. A többjegyűeknek elég az utolsó értékes jegyét venni, így a kiválasztott tényezők szorzata ugyanazzal a jeggyel végződik, amivel a
7⋅6(1⋅3⋅7⋅9)2
szorzat és mivel 3⋅7 utolsó jegye 1 és ezzel végződik 92 is, 7⋅6 pedig 2-vel végződik, így e szorzat utolsó jegye 2.
A többi tényezők közül elhagyhatjuk azokat, amelyeknek 1 az utolsó értékes jegye. Ezután válasszuk külön a 0-ra végződő tényezőket. A többi tényezőt hatosával csoportosítva összesen 11 olyan csoportot kapunk, melyek mindegyikében egy-egy 3-ra, 4-re, 6-ra, 7-re, 8-ra és 9-re végződő tényező van, tehát az első 100 természetes szám szorzata ugyanarra a jegyre végződik, mint amire a
2⋅(3⋅4⋅6⋅7⋅8⋅9)11

A zárójelben lévő szorzat utolsó jegye 8, 84-é 6 s így 88-é is, viszont páros számot 6-tal szorozva az utolsó jegy nem változik meg így a keresett számjegy megegyezik 2⋅83 utolsó jegyével. 83 utolsó jegye 2, tehát az első 100 természetes szám szorzatának utolsó értékes jegye 4.