|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. 1. Már régóta közismert. kedvelt találós kérdések az ilyenek: elküldtek valakit, hogy hozzon cigarettát forintért, még pedig vegyen krajcárosból, , és krajcárosból is. Miből mennyit hozott, ha cigarettát vett (és egy forint krajcár)?
Annyi mindenesetre világos, hogy a drágább cigarettákból csak keveset lehet venni, a cigaretták túlnyomó része krajcáros kell hogy legyen, hiszen annyi cigarettát veszünk ahány krajcárunk van. De pl. egy krajcáros cigaretta krajcárral drágább, mint ahány darab, tehát annyi krajcárost kell venni minden krajcáros mellé, hagy azok ára meg krajcárral kevesebb legyen, mint ahány darabot vettünk, tehát -at. Hasonlóan minden krajcáros cigarettához darab 2 krajcárost is kell venni, mert ez ad együtt cigarettát és az ára is krajcár. Végül minden krajcáros cigarettához darab krajcárost kell venni. Ha tehát az és krajcáros cigarettákból rendre , , darabot veszünk. akkor ezekhez darab krajcárost is kell venni s így az összes cigaretták száma (ami kell hogy legyen) Ez azonban határozatlan egyenlet, hiszen ismeretlen is van benne. Viszont ezekről az ismeretlenekről többet is tudunk, mint hogy kielégítik az (1) egyenletet, hiszen a cigaretták száma csak pozitív egész szám lehet. Ekkor pedig már újabb összefüggéseket is találhatunk. Nézzük meg például, hogy a baloldal második és harmadik tagja is osztható -mal. Vigyük át az első tagot a jobboldalra: Úgy kell tehát -et megválasztani, hogy a jobboldal osztható legyen -mal. -gyel mindjárt találunk ilyen értéket: . Válasszuk tehát -et -nek, ekkor marad az egyenletből és ennek , megoldása. Ha tehát ‐ darab és krajcáros cigarettát veszünk és darab krajcárost, akkor kell még darab krajcáros, hogy darab legyen és ezek ára összesen
2. Ezzel találtunk egy megoldását az (1) egyenletnek, de vajon aki bevásárolt, valóban így vásárolt-e? Vajon nincs-e több megoldása is, nem lehet-e végtelen sok megoldása is a feladatnak? Hogy végtelen sok megoldás nem lehet, azt könnyű látni, hiszen is, is, is pozitív, tehát a baloldal mindegyik tagja külön kisebb -nál: azaz | |
illetőleg, mivel , , még pozitív egészszámok is, így (Egy kis óvatossággal jobb korlátokat is találhattunk volna.) Mivel egész számokat keresünk, így minden változó csak véges számú értéket vehet fel, s így összesen is csak véges számú értékrendszer állítható össze belőlük. Persze távolról sem mind fogja kielégíteni az (1) egyenletet, de annyi bizonyos, hogy csak az ilyen értékrendszerek közül kerülhetnek ki az egyenletrendszer megoldásai, tehát mindenesetre véges a számuk. Kikereshetnénk ezeket úgy, hogy a most talált lehetséges megoldások mindegyiket végigpróbáljuk, de ez nagyon fáradalmas volna, még ha javítanánk is a talált felső korlátokon. A fent talált megoldás keresését nagyban megkönnyítette oszthatósági összefüggések felhasználása. Próbáljuk meg most ugyanezen az úton keresni az összes megoldásokat is. A (2) egyenletből találtunk alkalmas értéket. Választhatnánk-e -től különböző értékeket is -nek? -ból kellett -nek olyan többszörösét levonni, hogy -mal osztható szám maradjon. Ha -et levontunk, akkor maradt. Ha ebből még levonunk valamit, csak akkor kapunk -mal osztható számot, ha a levonandó is osztható -mal. -nek a -szorosa a legkisebb -mal osztható többszöröse, azonban már túl nagy, -ből levonva negatív számot adna, tehát nem lehet nagyobb -nél.
Így és csak a (3) egyenlet megoldása lehet. Ebből és nyilván egyformán lehetséges. megfelelő értékei és . Az , párra már rátaláltunk. Lehetséges azonban az is, hogy az , és krajcáros cigarettából sorra , , darabot vettünk. Ekkor darab krajcáros cigarettát kell venni és tehát ez is megoldása a feladatnak. Így megkaptuk a feladat két különböző megoldását és tudjuk, hogy több megoldás nincsen.
3. Nézzük meg, hogyan változik a megoldás, ha a követelmények ugyanazok maradnak, de az krajcáros cigaretták helyett krajcárosakat akarunk venni. Kövessük ismét azt a gondolatmenetet, ami az (1) egyenlethez vezetett minket. A változás most csak az, hogy egy krajcáros cigaretta mellé darab krajcárost kell mindig vennünk, mert ennyinek az ára kevesebb -vel, mint ahány darabot vettünk. Így most a krajcáros cigaretták számát jelölve -szel (1) helyett a egyenletet kell megoldanunk, amit így is írhatunk: Ez azonban lehetetlen, hiszen, mivel és relatív prímek, így -nek kellene oszthatónak lennie -mal, emellett pozitívnak kellene lennie, mert a baloldalon pozitív szám áll és is csak pozitív lehet. krajcáros, , és krajcáros cigarettákból tehát nem lehet úgy összesen darabot venni, hogy az áruk éppen forint legyen.
4. Próbáljunk akkor nem az , hanem a krajcáros cigaretták helyett venni krajcárosokat. Jelöljük -szel, -nal, -vel az , és krajcáros cigaretták számát. Mivel minden krajcáros cigarettához darab krajcárost kell venni, minden krajcároshoz darab és minden krajcároshoz darab -eset, hogy az átlagár pont egy krajcár legyen, így az összes cigaretták számára kell fennálljon. Innen Kell, hogy pozitív és -mal osztható legyen. Mivel is pozitív, csak leltet. Ekkor ami csak úgy lehet, ha , tehát . Ekkor a krajcáros cigaretták számára marad és Ez esetben tehát csak úgy vásárolhatunk be, hogy a krajcáros cigarettából -et, az -ösből -et, a -asból és -asból pedig ‐-et veszünk.
5. Azt a meglepő tényt tapasztaltuk, hogy egyetlen három ismeretlenes egyenletet is annyira határozottá válhat, hogy csak néhány, vagy éppen egyetlen megoldása legyen, sőt az is lehet, hogy nincs megoldása, ha további megszorításként azt kívánjuk, hogy a megoldás egész számokból, mégpedig pozitív egészekből álljon. Amikor egy egész együtthatós egyenletnek csak az egész megoldásait keressük, akkor diofantoszi, egyenletekről szoktunk beszélni, bár nem az egyenlet speciális tulajdonságáról van szó, hanem a megoldásokra kötünk ki megszorító követelményeket; így helyesebb volna diofantoszi problémáról beszélni.
Kétismeretlenes egyenlet összes egész megoldásának keresése
6. Az előzőkben tárgyalt problémákat látszólag szerencsésen adódó közös osztók alapján sikerült megoldanunk. Vajon valóban csak véletlen szerencse volt-e, hogy célhoz értünk, vagy van-e valamilyen általános eljárás ilyen feladatok megoldására? A továbbiakban ezt fogjuk megmutatni, hagy elsőfokú egyenletekre van általános megoldási eljárás. Először csak arra leszünk tekintettel, hogy a megoldásoknak egész számokból kell állniuk. Ez esetben általában még végtelen sok megoldása lesz egy egyenletnek, mégis egyszerű áttekintést fogunk tudni szerezni az összes megoldásokról. A bevezető feladatok háromismeretlenes egyenletekre vezettek, az alábbiakban vizsgáljunk először kétismeretlenes egyenleteket, tehát első feladatul tűzzük ki egész együtthatós alakú egyenletek összes egész megoldásainak megkeresését.
7. Nézzünk néhány példát: Azt, hogy és egész, úgy fogjuk tudni kihasználni, hogy az egyenletet átalakítjuk egy egész és egy tört részből álló egyenlőséggé. Ekkor a tört, csak látszólagos tört lehet, mely a lehetséges egyszerűsítések után egész számot ad és ebből fogunk tudni tovább következtetni. Itt kifejezésével tudunk ilyen alakot kapni: Mivel is, is egész, kell hogy is egész legyen. Innen és ezt kifejezéséhe helyettesítve Egyenletünk megoldásai tehát csak (, ) alakú számpárok lehetnek, ahol valamilyen egész számot jelent. (Természetesen a két helyen ugyanazt a számot.) Helyettesítsük ezeket az értékeket egyenletünk baloldalába: | |
Mivel kiesett az összefüggésből, így ezek az értékpárok bármilyen érték mellett megoldásait adják az egyenletnek. Állítsunk össze értéktáblázatba néhány megoldást szolgáltató , értékpárt, feltüntetve azt is, hogy milyen értékhez tartoznak:
Sikerült tehát az egyenlet megoldásait úgy állítani elő, hogy abban szerepel ugyan egy (újabb) ismeretlen , de ennek nemcsak bizonyos alkalmas értékei, hanem bármilyen egész értéke mellett megoldását kapjuk az egyenletnek, és a felírt kifejezések szolgáltatják az összes megoldást. Ez az egyszerű áttekintés a gyökök fölött, amire céloztunk. Egy ilyen, az eredeti feladat változói előállításához segítségül vett változót paraméternek szokás nevezni. Sikerült tehát az összes megoldásoknak egy paraméteres előállítását találnunk.
Figyeljük még meg, hogy az egymásutáni értékek mindig -tel növekednek, az értékek pedig -mal csökkennek, tehát igen egyszerű szabályosságú sorozatot alkotnak. Különben a paraméteres előállításból is világos, hogy ha -gyel nő, akkor növekszik -tel, pedig fogy -mal.
8. Nézzük most, hogy eljárásunk alkalmazható-e más egyenletekre is: innen Itt az utolsó törtnek kell valamilyen t egész számnak lennie. Ez maga is kétismeretlenes egyenlet -től különböző együtthatókkal. Eljárásunk mégsem volt eredménytelen, mert itt már kisebb együtthatók szerepelnek: a helyett már csak . Fejezzük ki innen -et: tehát kell hogy egész legyen: | |
Itt tehát több lépésben, de újra elértünk egy paraméteres előállításhoz. Behelyettesítve a kiindulási egyenlet baloldalába: | |
tehát itt is akármilyen egész értéke mellett megint megoldást kapunk. Néhány megoldást ismét összeállítunk:
Itt az egymásutáni -értékek -ével, az -értékek pedig -ével növekednek.
9. Az együtthatók fokozatos csökkenése kívánhat még sokkal több lépést is, mint az előző feladatban, de akkor is biztos, hogy véges számú lépésben célra vezet: Innen
Innen lépésről lépésre visszahelyettesítve:
Csak az ilyen alakú értékpárok adhatnak egész z értékek mellett megoldást. Ezeket az eredeti egyenletbe helyettesítve | |
tehát minden érték mellett valóban megoldást kapunk. Állítsunk össze ismét néhány megoldást:
10. Oldjuk még meg a következő egyenletet: Az előzőkhöz hasonlóan járva el
Itt azonban megakadtunk. Kövessük nyomon egyes lépéseinket. Ahhoz, hogy egész -érték mellett egész legyen, az első sorban szereplő -nek is valamilyen egész számnak kell lennie. Ha azonban egész, akkor csak úgy lesz egész, ha a második sorban -val jelölt kifejezés is egész szám, ha pedig is, is egész, akkor a harmadik sor -je is csak egész lehet. A negyedik sor szerint viszont bármilyen egész szám is, soha sem lehet egész. Ez azt jelenti, hogy az egyenletnek nem lehet egész megoldása. Ez valóban így is van és erre különösebb számítás nélkül is rájöhettünk volna, hiszen az egyenlet baloldalán álló is, is osztható -mal, tehát a baloldal bármilyen egész és értékre -mal osztható számot ad, a jobboldalon viszont nem osztható -mal, tehát semmilyen egész értékekre nem állhat fenn egyenlőség.
11. Ha viszont helyébe pl. -et írunk: akkor mindenekelőtt végigoszthatjuk az egyenletet -mal: innen
Az ilyen értékpárok ki is adják az összes megoldást, mert | |
12. Olyan eljárást találtunk tehát, amivel vagy meg tudjuk oldani egyenletünket, vagy kiderül, hogy az egyenlet nem oldható meg. Az utóbbi eset következik be akkor, ha az ismeretlenek együtthatóinak legnagyobb közös osztója nem osztója az ismeretlent nem tartalmazó tagnak. Későbben látni fogjuk azt is, hogy minden más esetben van megoldása az egyenletnek. Előbb azonban igyekezzünk a bevezetésül tárgyalt feladatokhoz közeledni. Egyrészt az 1‐4. pontban tárgyalt feladatokat nem ilyen eljárással oldottuk meg. Nem kínálkozik-e vajon egyszerűbb út más feladatoknál is? Másrészt tudunk-e mondani valamit általában a pozitív egész megoldásokról? Végül ott háromismeretlenes egyenletek léptek fel. Így felvetődik a kérdés, hogy található-e általános eljárás többismeretlenű elsőfokú egyenletek megoldására is.
13. Gyorsabb eljárást találhatunk bizonyos speciális feltételek esetében. Pl. az előző pontban tárgyalt egyenletről hasznos lesz észrevenni, hogy a osztója együtthatójának. Így az x-es tagot a jobboldalra víve és -et kiemelve Ebből látszik, hogy -nak oszthatónak kell lennie -tel. és azonban relatív prímek és tudjuk, hogy ha egy szorzat osztható egy számmal és az egyik tényezője relatív prím e számhoz, akkor a másik tényező külön osztható e számmal. Esetünkben tehát -nak kell oszthatónak lennie -tel:
Ezzel lényegében egy lépéssel sikerült rövidíteni az eljárást. Ehhez hasonló rövidítési lehetőségeket használtunk ki az 1-4. pontban is.
A nyert előállítás lényegesen különbözőnek látszik attól, amit a 11. pontban nyertünk, azonban írjunk helyett -t és máris az előbbi paraméteres előállítást kapjuk. A összefüggésből viszont minden egész értékhez egész adódik és megfordítva is egy egész értékhez a érték, ami szintén egész. A különbség tehát csak annyi, hogy az a megoldás, ami az egyik paraméter értékéhez tartozik, azt a másik paraméter szerinti előállításban az paraméterértéknél kapjuk meg és a kétféle paraméteres előállításban ellentétes sorrendben vannak a megoldások felsorolva.
14. Még lényegesebb könnyítést jelent, ha rátalálunk egy megoldásra. Nézzük pl. a egyenletet. Ha találunk -nek olyan többszörösét, amit -ből levonva -zel osztható számot kapunk, akkor már találtunk is egy megoldást. Egy ilyen többszörösnek -re kell végződnie, tehát például megfelel. Ezt -ből levonva marad, tehát vagyis , megoldása az egyenletnek. Vonjuk le -et a most felírt alakban felbontva a baloldalból: | |
vagy a második kifejezést a jobboldalra víve Mivel és relatív prímek, a jobboldal akkor és csakis akkor osztható -tel, ha osztható vele: Ezt egyenletünkbe írva | |
Egy megoldást ismerve tehát egy lépésben kaptuk meg az összes megoldásokat és azt is, hogy az így nyert paraméteres megoldás mindig gyököt állít elő és kiadja az összes gyököt, anélkül, hogy vissza kellett volna helyettesíteni az eredeti egyenletbe. Jegyezzük meg, hogy ehhez ismét lényegesen kihasználtuk az előző pontban dőlt betűkkel kiemelt tételt.
Ugyanezzel a gondolatmenettel belátható általában, hogy ha az egész együtthatós egyenletben és relatív prímek és , egy egész megoldása az egyenletnek, akkor minden egész -hez az egyenlet egy egész megoldását adja és előállatja az összes megoldást. Ebből egyszersmind az is leolvasható, hogy ha egy egész együtthatós (4) alakú egyenletnek van egész megoldása, akkor végtelen sok van.
15. Kérdés még az, hogy milyen esetekben van egész megoldása a (4) egyenletnek, mikor nincs. Láttuk, hogy megoldás csak akkor lehet, ha és legnagyobb közös osztója osztója a -nek is. Említettük, hogy ilyenkor van is mindig megoldás. Ezt lényegében eljárásunk is igazolja.
Tegyük fel, hogy teljesül a feltétel. Amennyiben az -nak és -nek -nél nagyobb közös osztója van, akkor ezzel végigoszthattuk az egyenletet, amint azt a 11. pontban tárgyalt példában tettük. Az osztás után és együtthatója már relatív prím lesz. Feltehetjük, hogy a (4) egyenlet már ezen osztás elvégzése után keletkezett, tehát és relatív prímek.
Vegyük másodszor észre azt is, hogy a megoldási eljárás végén nem lett volna szükséges az és számára nyert eredményt behelyettesíteni, mert eleve biztos, hogy az és számára kapott értékek a paraméter minden értéke mellett kielégítik az eredeti egyenletet. Lássuk ezt be pl. a 8. pontban tárgyalt feladaton. Haladjunk ismét visszafelé egyenleteink során. A összefüggéshez abból a meggondolásból jutottunk, hogy és az érék akkor és csakis akkor elégíti ki a egyenletet, ha és közül csak az egyiket választjuk tetszés szerint, a másikat viszont úgy, hogy kettőjük közt a összefüggés álljon fenn. Ez esetben , . Ha egész és csak ebben az esetben lesz és is egész. Tehát bármilyen értéke mellett ez a számpár megoldása a egyenletnek és az egyenlet minden megoldása felírható ilyen alakban.
Ehhez az egyenlethez viszont azon az alapon jutottunk, hogy és akkor és csak akkor elégíti ki az eredeti egyenletet, ha és közt fennáll a összefüggés és akkor és csak akkor kapunk egész és értékeket, ha is egész. Éppen láttuk azonban, hogy ennek szükséges és elégséges feltétele, hogy , legyen, tehát . Meggondolásainkból tehát, ha azokat pontosan követjük, az adódik, hogy , a egyenletnek megoldásit adja minden érték mellett Az egyenlet minden megoldása előállítható ilyen alakban, továbbá akkor és csak akkor kapunk egész megoldást, ha is egész.
16. Teljesen hasonlóan minden esetben belátható, hogy az eljárásunkkal nyert paraméteres előállítás a paraméter minden értéke mellett megoldását adja az egyenletnek, előállítja az összes megoldást és egész megoldást akkor és csak akkor ad, ha a paraméter értéke egész ‐ feltéve természetesen, hogy az utolsó osztásnál nem marad olyan tört, amelyben változó mar nem szerepel.
Azt kell tehát még belátnunk, hogy ez az eset nem fordulhat elő, ha és együtthatója két egymáshoz relatív prím szám. Ezt viszont jobb lesz általánosan és nem egy példa kapcsán gondolni végig. A (4) egyenletből -et kifejezve az | |
egyenlethez jutunk, ahol és az osztási hányados és maradék ha -t -val elosztjuk, tehát hasonlóan , és olyan egészek, amelyekre Ha itt , akkor a osztója -nek, mivel azonban és relatív prímek, ez csak úgy lehet, ha . Ekkor választhatjuk -et -nek és -et -nak, tehát , ez esetben az egyenlet tehát megoldható. Ha , akkor -nek is egésznek kell lennie és és közt az összefüggés áll fenn. Itt -gyel kell átosztanunk: | |
Ha itt , vagyis osztója -nak, akkor a (6) egyenlőségből következik, hagy -nek is osztója , tehát közös osztója -nak és -nek s így csak lehet. Ekkor választható -nak (-t választhatjuk -nek) s így Ez esetben tehát az egyenletnek van egész megoldása. Ellenkező esetben | |
ahol és között az összefüggésnek kell fennállnia, s hogy és egész legyen, -nek is egésznek kell lennie.
Hasonlóan haladhatunk lépesről lépésre tovább. Az ismeretlenek együtthatói sorra , , majd a osztás maradéka, azután az osztás maradéka és így tovább. Ezekre fennáll az egyenlőtlenségsorozat, vagyis az -k pozitív egész számok, amelyek állandóan csökkennek; egy ilyen sorozat azonban csak véges lehet, tehát van egy osztás, amelyik maradék nélkül elvégezhető. Ekkor azonban az előzőkhöz hasonlóan látható, hogy az utolsó osztó közös osztója az összes előző -knek, tehát -nak és -nek is, s így csak lehet. Ekkor a vele való osztás maradék nélkül elvégezhető, s így a szokásos módon visszahelyettesítve valóban nyerünk egész megoldásokat. Ezzel beláttuk, hogy a (4) egyenletnek van egész megoldása (és ekkor végtelen sok van) ha és relatív prímek, s így akkor is, ha és legnagyobb közös osztója maradék nélkül megvan -ben is.
A pozitív megoldások keresése
17. Keressük most az előző feladatokban a pozitív egész megoldásokat. A 7. pontban tárgyalt egyenlet egész gyökeinek értéktáblázata azonnal mutatja, hagy az egyetlen pozitív gyökpár az , . A gyökök sorozatában megfigyelt szabályosság folytán biztos, hogy a későbbi, fel nem sorolt megoldásokban is vagy , vagy negatív.
A 8. pontban tárgyalt egyenletnek viszont a (, ) értékpártól kezdve csupa pozitív megoldása következik. s így végtelen sok pozitív megoldása van. Nyilvánvaló is, hogy növekvő -hez egyre nagyobb értékek is tartoznak, mivel a két tag különbsége nem változhat. Ez különben a paraméteres előállításból is látható.
A 9. alatt tárgyalt egyenlet értéktáblázata nem tartalmaz pozitív gyökpárt, nyilván nem is tartalmazhat, hiszen ha is is pozitív, akkor a baloldal is, s így nem adhat -t.
18. A további feladatokhoz már nem készítettünk értéktáblázatot Írjuk fel itt algebrailag azt a követelést, hogy a megoldások pozitívak. Pl. a 11. pontban tárgyalt egyenlet (egyszerűsített alakjában írtuk mindjárt) megoldásai Mindkettőnek pozitívnak kell lennie, amit úgy írhatunk jelekkel, hogy nagyobbak -nál : Az első csak akkor állhat fönn, ha ,,elég kicsi'', utóbbi pedig, ha ,,elég nagy''. Így megengedett értékeit két korlát közé fogjuk tudni szorítani, még pedig | |
Mivel még egész is, így azt kapjuk, hogy Ilyen szám azonban nem létezik, nemcsak az összes egész számok közt, de az összes valós számok közt sem. (Ezt is láthattuk volna mindjárt az egyenletről is, mert ha és pozitív egész, tehát legalább , akkor a baloldalnak már az első tagja is nagyobb, mint a jobboldal.)
Keressük végül a 14. pontban tárgyalt egyenlet pozitív megoldásait. Ezek a paraméter azon értékeihez tartoznak, amelyekre innen A , , értékekhez tehát pozitív egész gyökök tartoznak, ezek:
19. Az eddigiekben az együtthatók előjel- és nagyságviszonyaiból meg tudtuk állapítani, hogy van-e pozitív gyök és végtelen sok van-e. A következő példa azonban azt fogja mutatni, hogy nem mindig van pozitív megoldás akkor sem, ha nem látszik ,,ránézésre'', hogy nincs pozitív megoldás. A egyenletről pl. sem az előjelek, sem az együtthatók nagysága még nem ad alapot annak eldöntésére, hogy van-e pozitív gyök, ill. olyan következtetésre, hogy nem volna ilyen. Alkalmazzuk tehát a kérdés eldöntésére az előző pont eljárását. Oldjuk először meg az egyenletet: | |
A pozitív gyököt szolgáltató -értékekre tehát fenn kell állnia az | |
vagy mivel egész, az egyenlőtlenségeknek, ilyen érték azonban nem létezik, tehát az egyenletnek nincs pozitív egész megoldása, bár ez nem volt ránézésre nyilvánvaló.
20. Min múlik hát, hogy van-e vagy nincs pozitív megoldás, ha az együtt hatók előjele és nagysági viszonya sem ad erre biztos választ? Nyilván ismét azon követelésen, hogy a megoldás még egész szám is legyen. Az előző feladatban talált feltételnek pl. eleget tesz érték, a számegyenes egy -nél nagyobb (pontosan hosszúságú szakaszának minden valós száma. Ezek közt végtelen sok racionális szám is akad, egész szám azonban már nem.
Világosabb képet kapunk a helyzetről, ha valóban képet próbálunk alkotni, tehát grafikusan ábrázoljuk a megoldásokat. Ha a 7., 8. és 9. pontokban készített értéktáblázatok értékpárjait grafikusan ábrázoljuk, akkor a megoldásokat ábrázoló pontok egy-egy egyenesen látszanak sorakozni. (1. ábra.) 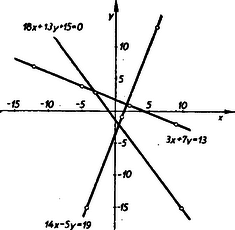 1. ábra
Ez nemcsak látszat, hanem valóban így is kell lennie éppen az egymásután következő megoldások közt megfigyelt szabályosság alapján. Láttuk pl., hogy a egyenlet paraméteres megoldásában értékét egyenként növelve értéke mindig -tel nő, értéke pedig mindig -mal fogy. Így minden pontból a következőbe ugyanolyan meredekséggel lefelé haladva jutunk el, tehát valóban egy egyenesen sorakoznak a megoldásokat ábrázoló pontok. (Ha értékéül nemcsak egész számokat veszünk tekintetbe, akkor az egyenes bármely pontjának , koordinátáit megadják alkalmas érték mellett az , kifejezések.)
Teljesen hasonló a helyzet a többi egyenletnél is. Általában ha egy (5) alakú egyenletrendszer egyes értékekhez tartozó megoldáspárjait grafikusan ábrázoljuk, ezek mindig egy egyenesen sorakozó pontok lesznek.
Az egész megoldásoknak olyan pontok felelnék meg, amelyeknek mindkét rendezője, mindkét koordinátája egész szám. Ha ezeket ábrázoljuk, ezek egybevágó kis négyzetek csúcsain rácsszerűen helyezkednek el a síkban. (2. ábra.) 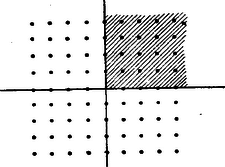 2. ábra
Az ilyen pontokat röviden rácspontoknak fogjuk nevezni. A pozitív megoldásokat olyan rácspontok ábrázolják, amelyeknek mindkét koordinátájuk pozitív egész szám. Ezeket a sík azon szektorába eső rácspontok ábrázolják, amelyet az -tengelynek is, az -tengelynek is a pozitív fele határol. Ezt szokás röviden első síknegyednek nevezni.
A kétismeretlenes elsőfokú egyenletnek tehát ábrázolásban egyenes felel meg. Az egész megoldásokat az egyenesre eső rácspontok ábrázolják, a pozitív egész megoldásokat az első síknegyedbe eső rácspontok. A pozitív egész megoldások keresésének tehát az a kérdés felel meg, hogy átmegy-e az egyenletet képviselő egyenes első síknegyedbeli rácsponton.
21. Nézzük először is, hogyan helyezkedhet el egy egyenes az első síknegyedhez képest. Lehet, hogy egyik határát sem metszi, mint a 3. ábra (I) egyenese.  3. ábra
Lehet, hogy az egyenes mind a két határvonalat metszi s így egy véges darabja esik az első síknegyedbe, mint a (II) egyenesnek. Végül lehet, hogy az egyenes csak egy pontban metszi át a síknegyed határát és onnan kezdve a belsejében halad, mint a (III) vagy a (IV) egyenes. Mostmár az, hogy a három eset közül melyik fordul elő, eldönthető tisztán az együtthatók előjeléből; belátható könnyen, hogy ha az egyenletben és ellenkező előjelű, akkor mindig a harmadik eset áll fenn. Ha viszont és egyező előjelű, akkor aszerint következik be az első, vagy a második. eset, amint előjele ellenkező, vagy olyan, mint -é és -é. Ennek igazolásától itt eltekintünk, mert a pozitív megoldásokra, mint már láttuk, úgy sem kapunk ebből teljes felvilágosítást.
22. Az első esetben természetesen nem lehet pozitív megoldása az egyenletnek, hiszen az egyenesnek nincs pontja az első síknegyedben. Ez különben azonnal látható abból is, amit az együtthatók előjeléről ebben az esetben mondtunk.
Belátható az is, ha nem is ilyen könnyen, hogy a harmadik esetben viszont végtelen sok pozitív egész megoldása van az egyenletnek, ha egyáltalán van egész megoldása.
Azt már láttuk ‐ a. 14. Pontban ‐ hogyha egy egész együtthatós elsőfokú egyenletnek van egész megoldása, akkor van végtelen sok. Pontosabban az is igaz, hogy ezen megoldásokat egy egyenesen egyenlő távolságban sorakozó rácspontok ábrázolják. Hiszen tudjuk, hogy a megoldásokat pl. növekvő értékek szerint elrendezve ezen értékek mindig ugyanannyival növekednek. A 8. pontban tárgyalt egyenletnek pl. egy egész megoldása volt , és ezen túl -önként növelve vagy csökkentve -et találunk egész megoldásokat. Ez geometriailag azt jelenti, hogy az egész megoldásoknak megfelelő rácspontok az -tengellyel párhuzamos, egymástól egységnyi távolságban következő egyeneseken helyezkednek el, ezek az egyenesek metszik ki e rácspontokat az egyenletet szemléltető egyenesből. Ezen párhuzamos egyenesek azonban egyenlő szakaszokat metszenek ki és éppen ezt akartuk igazolni.
Ha most egy egyenletet olyan egyenes szemléltet, amelyiknek egy végtelen félegyenese esik az első síknegyedbe és esnek az egyenesre rácspontok, akkor ezek az első síknegyedben is egyenlő távolságban követik egymást, tehát végtelen sok rácspont van az egyenes első síknegyedbe eső részén. Az egyenletnek tehát, amit az egyenes szemléltet, végtelen sok pozitív egész megoldása van.
23. Hátra van tehát még a második eset. amikor az egyenletet ábrázoló egyenesnek egy véges szakasza esik az első síknegyedbe.
Ábrázoljuk a 18. és 19. pontban szereplő három egyenletet (4. ábra), mindegyik ilyen egyeneshez vezet, kettőn közülük nincs rácspont, a harmadikon van három is.
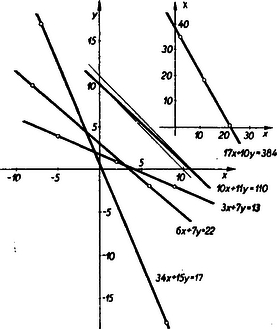 4. ábra
Ilyen a már ábrázolt egyenlet képe is. Ennek egy pozitív megoldása van. Teljesen független az egyenesen lévő rácspontok száma az egyenes első síknegyedbe eső darabjának a hosszától. Rajzoljuk meg pl. a (,), (,) pontokat összekötő egyenest és azt is, amelyik a (,), (,) pontokat köti össze. Ezek mindegyike igen gazdag rácspontokban, minden egész értékhez tartozó pontjának értéke is egész. A két egyenes közt azonban egyetlen rácspont sincs. Így ha pl. az elsőnek a (,) pontját a második (,) pontjával kötjük össze, akkor a keletkező egyenesnek e két pontja közé nem eshetik rácspont. De az egyenesnek éppen ez a szakasza esik az első síknegyedbe. Így annak az egyenletnek, amelyiket ez az egyenes ábrázol, nincs pozitív egészszámokból álló megoldása. Könnyű látni, hogy a egyenletnek ez az egyenes a képe, mert az egyenletnek , is és , is megoldása, tehát az ezeknek megfelelő pontokat összekötő egyenes a képe. De ugyanúgy látható, hogy a egyenletnek, mely a (,), (,) pontokon megy át, szintén nincs pozitív egészekből álló megoldása és hasonlóan készíthető egyenlet (és sok más módon is.); amelyet ábrázoló egyenesnek tetszés szerint nagy darabja esik az első síknegyedbe, még sincs egyetlen pozitív egészekből álló megoldása sem, bár egész megoldása van.
24. Az ilyen egyenletek pozitív megoldásainak létezését legkönnyebben úgy dönthetjük el, ha megkeressük mindjárt a pozitív megoldásokat úgy, ahogyan azt a 18 ‐ 19. pontban tettük. Célszerű ez abban az esetben is, amikor végtelen sok pozitív megoldás van, ha pontosan akarjuk tudni, hogy honnan kezdve következnek ezek a pozitív megoldások. Az eljárás tehát az, hogy először is megkeressük az egyenlet egész megoldásainak egy paraméteres előállítását, azután felírjuk azt a követelményt, hogy mindkét összetevő pozitív (tehát -nál nagyobb) legyen és az így adódó egyenlőtlenségekből meghatározzuk a paraméter azon egész értékeit, amelyek mindkét feltételt kielégítik. (Természetesen a paraméter számára könnyen adódhatnak negatív értékek is, csak a hozzájuk tartozó megoldásoktól kívánjuk, hogy pozitívok legyenek.)
25. Előfordulhat az is, hogy nem pozitivitást követelünk a megoldástól, hanem más nagysági kikötések vannak adva.
Valaki így szól: Ötven forintból vettem egy sakktáblát. Csupa aprópénzt kaptam vissza. Mikor a maradék pénzem számoltam, kiraktam a táblára úgy, hogy minden mezőn ugyanannyi pénz volt. Aztán vettem figurákat. A futóért, huszárért háromszor, a toronyért négyszer, a vezérért kilencszer, a királyért pedig tizenhatszor annyit fizettem, mint egy gyalogért és maradt forintom. Vajon mennyi pénze volt az illetőnek és mire mennyit adott ki?
Ha fillért tett számolgatás közben egy mezőre, akkor a tábla vétele után fillér pénze maradt. Ha egy gyalog ára fillér volt, akkor a figura ára volt, tehát Oldjuk meg először is az egyenletet. Osszunk -vel:
Mivel az utolsó egyenlet baloldala osztható -tel, pedig relatív prím hozzá, így osztható -tel: , a baloldal pedig csak úgy lehet páros, ha is az: . Így
26. Mint az várható volt, végtelen sok pozitív megoldás van. Mi azonban nemcsak azt tudjuk a megoldásokról, hogy pozitív egészszámok, hanem azt is, hogy a sakkozónak vásárlás előtt forintja volt, tehát a táblavétel után már biztosan kevesebb. Így az feltételek mellett fenn kell állnia a feltételnek is. Ezeket egyenként megoldva -re | |
Az első két egyenlőtlenségből az következik, hogy nem lehet negatív egész, az utolsó szerint viszont pozitív egész sem lehet, tehát Így a tábla ára fillér, azaz volt, a figuráké pedig . Látjuk, hogy végtelen sok pozitív megoldás esetén is határozottá lett a megoldás egy további nagysági korlátozás folytán. Nézzük meg ismét mit jelent ez grafikusan (5. ábra). 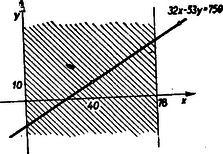 5. ábra
A (6) feltételből tehát pozitív egész számokról lévén szó Az ezen feltételt kielégítő pontok az ábrán vonalkázott egy irányban végtelen sávba esnek. Egy ilyenbe egy nem függőleges egyenesnek mar legfeljebb véges sok rácspontja eshet.
Többismeretlenes egyenletek és egyenletrendszerek
27. Térjünk vissza végezetül a bevezető feladatokhoz, azok közül is az elsőhöz. krajcárért cigarettát vettünk, azok közt volt , , és krajcáros. Háromismeretlenű egyenletrendszerhez jutottunk, ahhoz is ravaszkodással, de minden ravaszkodás nélkül is eljárhattunk volna: Ha az , és krajcáros cigaretták számát, mint ott, , és -vel, a krajcárosokét pedig -vel jelöljük, akkor a cigaretták száma az áruk pedig | |
Ha innen -t kiküszöböljük, a második egyenlet kétszereséből levonva az elsőt, akkor jutunk az eredetileg tárgyalt egyenlethez.
Általában kettőnél több ismeretlen esetén már egyenletrendszer is lehet határozatlan (pl. ha kevesebb egyenletünk van, mint amennyi az ismeretlen). Ezekkel kapcsolatban is felmerül a kérdés, vajon mit tudunk az egész megoldásokról mondani, ha egész együtthatós elsőfokú egyenletrendszerről van szó.
Először általában is azt tesszük, mint az előző feladatban: kiküszöbölünk annyi ismeretlent, amennyit csak lehet, míg végül csak egy egyenletünk marad. Az így nyert egyenlettel viszont ugyanúgy járunk el, mint két ismeretlen esetén: kifejezzük azt az ismeretlent, amelyiknek legkisebb abszolút értékű az együtthatója és azután lépésről lépésre ismételjük az eljárást. Lássunk erre is egy példát. Mindjárt csak egy egyenletet adunk meg:
Ahhoz. hogy egész és mellett is egész legyen, -nek is egésznek kell lennie, viszont nyilván ha és egész, akkor és is az. Nem adódott semmilyen kikötés -re, tehát is jelenthet bármilyen egészszámot. A kapott értékeket visszahelyettesítve az egyenlet baloldalába
azok valóban akármilyen és érték mellett kielégítik az egyenletet. Az az egyetlen különbség adódott tehát csak, hogy most nem egy, hanem két paraméter szerepel (egyik gyanánt maga az egyik változó szolgál, amelyek helyébe bármilyen egész számokat írva megoldást kapunk és ilyen alakban minden megoldás előállítható.
Nem bocsátkozunk bele a részletek elemzésébe. Az előzőkhöz hasonlóan látható, hogy akárhány ismeretlen esetén elsőfokú, egész együtthatós egyenletnek akkor és csak akkor van egész megoldása ‐ és akkor végtelen sok ‐ ha az összes változók együtthatóinak legnagyobb közös osztója osztója az állandó tagnak is. Ekkor eggyel kevesebb paraméter segítségével állítható elő az általános megoldás, mint ahány ismeretlen van.
Ugyancsak nem foglalkozunk itt részletesebben a pozitív megoldások kérdésével. ami újabb elvi problémát nem okoz, de a feltételül kapott egyenlőtlenség-rendszer megoldása szokatlan problémát jelent. Ezekre még feladatok kapcsán vissza fogunk térni.
Alexandriai Diofantosz életéről vajmi keveset tudunk, valószínűleg i. u. 360 körül élhetett. Ö volt as első, aki nem kapcsolódva geometriai képhez, foglalkozott a négy alapművelettel (beleértve természetesen a hatványozást is) felépíthető problémákkal. Ezzel az európai kultúrában ő volt az első, aki az algebra problémáját érdemben felvetette és jelentős eredményeket is mutatott fel. Számelméleti problémákkal csak annyiban került kapcsolatba, hogy a görögök csak a pozitív racionális számot ismerték el számnak, s így ő is az egyenletek pozitív racionális megoldását kereste. Nem sok követőre talált. Műveire csak E. G. Bachet de Méziriac (olv. Basé dö Méziriak) francia matematikus hívta fel a figyelmet a XVI. század végén. Az elsőfokú egyenlet megoldása Diofantosznak nem okozott problémát, hiszen racionális megoldás mindig van. Az egész megoldások keresésének kérdését Bachet vetette fel. A cikkben ismertetendő megoldási eljárás is Bachet-től ered. |
PDF | MathML