Kezdőlap


Cím:	Az 1953. évi Rákosi Mátyás matematikai tanulmányi verseny I. fordulója
Füzet:	1953/május, 129 - 140. oldal	PDF \| MathML
Témakör(ök):	OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ez idén a Rákosi Mátyás matematikai versenyen már csak a gimnáziumok és ip. technikumok III. és IV. oszt. tanulói indulhattak. A verseny I. fordulója március 10-én folyt le az egyes iskoláknál. Az alábbi 3 feladat volt kitűzve (munkaidő: 5 óra):

1. Megoldandó a következő egyenletrendszer:

\begin{matrix} x + x y + y + 5 = 0 & (1) \\ x^{2} y + x y^{2} + 6 = 0. \end{matrix}

2. Az

A B C D

négyzet belsejében lévő

P

pontnak az

A

B

C

csúcsoktól való távolsága rendre

2

3

4

. Szerkesszük meg e négyzetet és számítsuk ki a területét.
3. Megoldandó a következő egyenlet:

\begin{matrix} sin x + cos x = \frac{cos 2 x}{1 - 2 sin x}, \end{matrix}

(2)

Beadtak összesen 2943 dolgozatot, amelyeknek eredménye alapján összesen 189 tanuló (6,4

%

) került a döntőbe. (Tekintve, hogy számos résztvevő nem adott be dolgozatot, az összes indulók száma 3000-nél jóval többre tehető.) Részletes adatok megyék és iskolafajok szerint az itt közölt táblázatos kimutatásban találhatók. A döntőbe került tanulók megoszlása nemek szerint: 178 fiú, 11 lány. Örömmel állapítottuk meg, hogy a döntőbe került 189 tanuló közül 92-en lapunk feladatmegoldói.
A döntő április 12-én folyt le a megyeszékhelyeken és Budapesten a József Attila gimnáziumban. A döntőről a legközelebbi (szeptemberi) számban számolunk be.

Alább közöljük az I. forduló feladatainak megoldásait.

1. feladat.

I. megoldás: Az első egyenletből

\begin{matrix} y (x + 1) + x + 5 = 0. \end{matrix}

Itt

x

nem lehet

-

1, így

y

-t kifejezhetjük:

\begin{matrix} y = - \frac{x + 5}{x + 1} . \end{matrix}

Ezt a második egyenletbe helyettesítve és rendezve az

\begin{matrix} x^{4} + 5 x^{3} - 11 x^{2} - 37 x - 6 = 0 \end{matrix}

egyenlethez jutunk. Vizsgáljuk meg, hogy van-e ennek racionális gyöke. Tudjuk, hogy ha van ilyen megoldás, akkor annak számlálója az állandó tagnak,

- 6

-nak, nevezője pedig a legmagasabb fokú tag együtthatójának, tehát esetünkben

1

-nek osztója. Így csak az

x = \pm 1

\pm 2

\pm 3

és

\pm 6

értékek jöhetnek számításba. Kipróbálva azt találjuk, hogy

- 2

és

3

valóban gyök is. Így az egyenlet baloldalából kiemelhetőnek kell lennie az ezekhez tartozó gyöktényezők szorzatának, az

\begin{matrix} (x + 2) (x - 3) = x^{2} - x - 6 \end{matrix}

polinomnak és valóban negyedfokú egyenletünk baloldala így írható:

\begin{matrix} (x^{2} - x - 6) (x^{2} + 6 x + 1) . \end{matrix}

Így a már megtalált gyökökön kívül gyökei még az egyenletnek az

\begin{matrix} x^{2} + 6 x + 1 = 0 \end{matrix}

egyenlet gyökei. Az összes gyökök tehát

\begin{matrix} x_{1} = - 2, x_{2} = 3, x_{3} = - 3 + 2 \sqrt[]{2}, x_{4} = - 3 - 2 \sqrt[]{2} . \end{matrix}

és a megfelelő

y

-értékek:

\begin{matrix} y_{1} = 3, y_{2} = - 2, y_{3} = - 3 - 2 \sqrt[]{2}, y_{4} = - 3 + 2 \sqrt[]{2} . \end{matrix}

\begin{matrix} Kimutatás az 1953. évi Rákosi Mátyás matematikai verseny I. fordulójáról \\ megyék és iskolafajok szerint \\ Beadott dolgozatok & Döntőbe került \\ Megyék és Budapest & Gim- & Ip. \\ Gimnázium & Ip. techn. & Összesen & názium & Techn. & Összesen \\ 1. Baranya & 93 & 39 & 132 & 7 & ‐ & 7 \\ 2. Bács-Kiskún & 91 & 4 & 95 & 4 & ‐ & 4 \\ 3. Békés & 147 & 19 & 166 & 10 & 2 & 12 \\ 4. Borsód & 142 & 42 & 184 & 4 & 4 & 8 \\ 5. Csongrád & 94 & 61 & 155 & 8 & 4 & 12 \\ 6. Fejér & 27 & 13 & 40 & 2 & ‐ & 2 \\ 7. Győr-Sopron & 107 & 19 & 126 & 18 & ‐ & 18 \\ 8. Hajdu-Bihar & 100 & 25 & 125 & 4 & 1 & 5 \\ 9. Heves & 29 & 10 & 39 & 4 & ‐ & 4 \\ 10. Komárom & 100 & 26 & 126 & 9 & ‐ & 9 \\ 11. Nógrád & 25 & 12 & 37 & 3 & ‐ & 3 \\ 12. Pest & 68 & 2 & 70 & 3 & ‐ & 3 \\ 13. Somogy & 23 & 6 & 29 & 4 & ‐ & 4 \\ 14. Szabolcs‐Szatmár & 68 & 16 & 84 & 2 & ‐ & 2 \\ 15. Szolnok & 106 & 5 & 111 & 5 & 1 & 6 \\ 16. Tolna & 83 & ‐ & 83 & ‐ & ‐ & ‐ \\ 17. Vas & 118 & 3 & 121 & 2 & ‐ & 2 \\ 18. Veszprém & 100 & 5 & 105 & 9 & ‐ & 9 \\ 19. Zala & 28 & 6 & 34 & 3 & ‐ & 3 \\ 20. Budapest & 1011 & 70 & 1081 & 64 & 12 & 76 \\ Összesen & 2560 & 383 & 2943 & 165 & 24 & 189 \end{matrix}

II. megoldás: A második egyenlet így írható

\begin{matrix} x y (x + y) + 6 = 0 \end{matrix}

és vegyük észre, hogy az

u = x + y

és

v = x y

kifejezések összege és szorzata van megadva:

\begin{matrix} u + v = - 5, u v = - 6. \end{matrix}

u

és

v

tehát a

\begin{matrix} t^{2} + 5 t - 6 = 0 \end{matrix}

egyenlet két gyöke, vagyis

\begin{matrix} u_{1} = \frac{- 5 + 7}{2} = 1, v_{1} = \frac{- 5 - 7}{2} = - 6, \end{matrix}

vagy fordítva

\begin{matrix} u_{2} = - 6, v_{2} = 1. \end{matrix}

Mivel ezek jelentése

x + y

, ill.

x y

, tehát

x

és

y

\begin{matrix} z^{2} - z - 6 = 0 \end{matrix}

és a

\begin{matrix} z^{2} + 6 z + 1 = 0 \end{matrix}

egyenlet két gyöke lehet. Az első egyenletből

\begin{matrix} x_{1} = 3, y_{1} = - 2; x_{2} = - 2, y_{2} = 3. \end{matrix}

A második egyenletből

\begin{matrix} x_{3} & = - 3 + 2 \sqrt[]{2}, & y_{3} & = - 3 - 2 \sqrt[]{2}; \\ x_{4} & = - 3 - 2 \sqrt[]{2}, & y_{4} & = - 3 + 2 \sqrt[]{2} . \end{matrix}

2. feladat.

I. megoldás:
a) A terület kiszámítása: Képzeljük a feladatot megoldottnak. A betűzést az 1. ábra mutatja.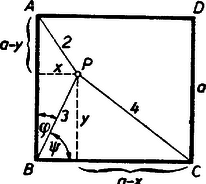

1. ábra

\begin{matrix} x^{2} + {(a - y)}^{2} = 4, & (1) \\ x^{2} + y^{2} = 9, & (2) \\ {(a - x)}^{2} + y^{2} = 16, & (3) \end{matrix}

egyenletrendszerből akarjuk kiszámítani

a

-t, illetőleg

a^{2}

-et. (2)-ből levonva (1)-et és (3)-ból (2)-t

\begin{matrix} 2 a y - a^{2} = 5, & (4) \\ a^{2} - 2 a x = 7. & (5) \end{matrix}

A (2) alatti egyenletet

4 a^{2}

-tel szorozva, továbbá (5) és (4)-ből

2 a x

és

2 a y

értékét behelyettesítve

\begin{matrix} {(a^{2} - 7)}^{2} + {(a^{2} + 5)}^{2} = 36 a^{2} . \end{matrix}

z = a^{2}

új ismeretlent vezetve be

\begin{matrix} 2 z^{2} - 40 z + 74 = 0, vagyis z^{2} - 20 z + 37 = 0, \end{matrix}

ahonnan

\begin{matrix} a^{2} = z = 10 \pm \sqrt[]{63} . \end{matrix}

Tehát

\begin{matrix} a_{1}^{2} = 10 + 3 \sqrt[]{7} \approx 17, 9374, a_{2}^{2} = 10 - 3 \sqrt[]{7} \approx 2, 0629. \end{matrix}

a_{2}

oldalú négyzetnek

P

nincs a belsejében, mert

\sqrt[]{2} a_{2} < 3 = B P

b) A négyzet megszerkesztése: A

P

pontról azt tudjuk, hogy az

A

és

B

ponttól mért távolságainak az aránya

2 : 3

, a

B

és

C

ponttól vett távolságainak aránya pedig

3 : 4

. Ennek alapján a négyzet megszerkesztése a következőképpen történhet: rajzoljunk tetszés szerinti

A' B' C' D'

négyzetet és azt az Apollonius-kört, amelynek pontjaira nézve az

A'

és

B'

ponttól mért távolságok aránya

2 : 3

, továbbá azt, amely pontjainak a

B'

és

C'

ponttól mért távolságai aránya

3 : 4

. E két körnek van

2

metszéspontja

P

és

P^{*}

(2. ábra).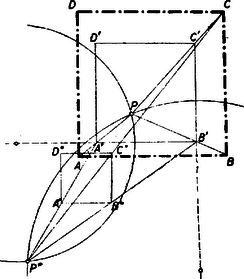

2. ábra

Nagyítsuk vagy kicsinyítsük a négyzetet a

P

(ill.

P^{*}

) pontból, mint hasonlósági centrumból úgy, hogy

A P

(ill.

A P^{*}

)

2

hosszegység legyen. Az egyik megoldásban a

P

pont a négyzeten kívül van.

II. megoldás:
a) A terület kiszámítása: A következő út, amelyen több versenyző elindult, jó példa arra, hogy nem minden helyes összefüggés alkalmas a feladat áttekinthető megoldására.
Aszerint, amint

P

A B C_{▵}

-ben, vagy

A C D_{▵}

-ben van, fennáll a területekre vonatkozó

\begin{matrix} t_{A B P} + t_{B C P} + t_{A C P} = \frac{a^{2}}{2} \end{matrix}

egyenletek egyike, ahol

a

a keresett négyzet oldala. Az egyes háromszögek oldalhosszai

2

3

a

, ill.

3

4

a

, ill.

2

4

a \sqrt[]{2}

, így Heron képlete szerint

\begin{matrix} t_{A B P} & = \sqrt[]{\frac{5 + a}{2} \cdot \frac{a + 1}{2} \cdot \frac{a - 1}{2} \cdot \frac{5 - a}{2}} = \frac{1}{4} \sqrt[]{(25 - a^{2}) (a^{2} - 1)}, \\ t_{B C P} & = \sqrt[]{\frac{7 + a}{2} \cdot \frac{a + 1}{2} \cdot \frac{a - 1}{2} \cdot \frac{7 - a}{2}} = \frac{1}{4} \sqrt[]{(49 - a^{2}) (a^{2} - 1)}, \\ t_{A C P} & = \sqrt[]{(3 + \frac{a}{\sqrt[]{2}}) (\frac{a}{\sqrt[]{2}} + 1) (\frac{a}{\sqrt[]{2}} - 1) (3 - \frac{a}{\sqrt[]{2}})} = \frac{1}{2} \sqrt[]{(18 - a^{2}) (a^{2} - 2)} . \end{matrix}

Ezeket a fenti egyenletbe helyettesítve egy tagot a baloldalra kellene vinni, majd háromszori négyzetre emelés után jutnánk algebrai egyenletre, mely közben nem egyszerűsödik lényegesen. Így ezen az úton nem jutunk gyakorlatilag kezelhető megoldásra, bár teljesen helyesen írtunk fel közben egy egyetlen ismeretlent tartalmazó egyenletet.
Azért a Heron-képlettel is célhoz érhetünk, a következő módon. (A jelölést az 1. ábra mutatja.) Az előbbiek alapján

\begin{matrix} 4 t_{A B P}^{2} = {(2 t_{A B P})}^{2} = \frac{1}{4} (25 - a^{2}) (a^{2} - 1) = {(a x)}^{2} = a^{2} x^{2}, \end{matrix}

(1)

\begin{matrix} 4 t_{B C P}^{2} = {(2 t_{B C P})}^{2} = \frac{1}{4} (49 - a^{2}) (a^{2} - 1) = {(a y)}^{2} = a^{2} y^{2}, \end{matrix}

(2)

továbbá

x^{2} + y^{2} = 3^{2} = 9

. (3)

(1) és (2)-ből

x^{2}

, ill.

y^{2}

értékét (3)-ba helyettesítve, rendezés után az I. megoldásban szereplő

\begin{matrix} a^{4} - 20 a^{2} + 37 = 0 \end{matrix}

egyenletet nyerjük.

b) A négyzet megszerkesztése: Tegyük fel, hogy a keresett négyzet oldalhosszát (pl. az I. megoldásban megadott módon) kiszámítottuk:

\begin{matrix} a - \sqrt[]{10 + 3 \sqrt[]{7}} . \end{matrix}

Ez az eredmény és általában minden olyan formula, amelyik az adott mennyiségekből a 4 alapművelet (ide tartozik az egész kitevőjű hatványozás) és véges számú négyzetgyökvonás alkalmazásával előállítható, mindjárt módot is ad a kérdéses adat megszerkesztésére. (Lásd 544. sz. kitűzött feladatot.) Esetünkben, ha ismert az egység (pl. a

3

és

2

hosszúságú távolságok különbsége),

a

nem egyéb, mint olyan derékszögű háromszög átfogója, melynek befogói

\sqrt[]{10}

ill.

\sqrt[]{3 \sqrt[]{7}}

. Ez utóbbi távolságot úgy szerkeszthetjük meg, hogy előbb megszerkesztjük

\sqrt[]{7}

-et és azután

\sqrt[]{7}

és

3

között a mértani középarányost.

\sqrt[]{7}

pl. olyan derékszögű háromszög befogójaként nyerhető, amelynek ismert befogója

3

egység, átfogója

4

egység (3. ábra).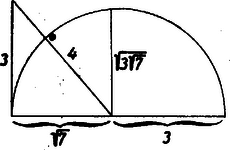

3. ábra

\sqrt[]{10}

olyan derékszögű háromszög átfogója, amelynek befogói

3

és

1

egység (4. ábra).

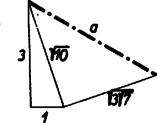4. ábra

(Teljesen hasonlóképpen szerkeszthető meg a másik gyök:

\sqrt[]{10 - 3 \sqrt[]{7}}

is.

Megjegyzés: Lényeges volt, hogy szerkesztéseinkben csak a kiindulásul adott távolságokat és az azokból megszerkesztetteket (pl.

\sqrt[]{7}

\sqrt[]{3 \sqrt[]{7}}

) használtuk fel. Többen a számítással kapott eredményt (irracionális szám közelítő értékét) mérőlécről igyekeztek körzőnyitásba venni és ezzel a távolsággal >>szerkesztettek<< négyzetet. (Valójában csak >>rajzoltak<< négyzetet). Ilyen módon természetesen a legtöbb szerkesztés nem okozna gondot annak, aki ismeri a trigonometriát. Ilyen eljárást azonban nem nevezünk >>szerkesztés<<-nek, bármilyen jó is legyen gyakorlati szempontból, mert a megengedett szerkesztő eszközök között nem szerepel a távolság- és szögmérő, hanem csak a körző és vonalzó.

III. megoldás:
a) A terület kiszámítása: Térjünk vissza az 1. ábrához. Legyen

A B P ∢ = φ

P B C ∢ = ψ

. Számítsuk ki

cos φ

-t, ill.

cos ψ

-t a cosinus-tétel segítségével az

A B P

, ill.

P B C

háromszögekből. A kifejezésekben egyedül az

A B = B C = a

négyzetoldal lesz ismeretlen. Erre pedig abból kaphatunk egy egyenletet, hogy

φ + ψ = 90^{\circ}

, s így

cos ψ = sin φ

, vagyis

\begin{matrix} cos^{2} φ + cos^{2} ψ = cos^{2} φ + sin^{2} φ = 1. \end{matrix}

(1)

A B P

háromszögböl

\begin{matrix} a^{2} + 3^{2} - 6 a cos φ = 2^{2}, \end{matrix}

ahonnan

\begin{matrix} cos φ = \frac{a^{2} + 3^{2} - 2^{2}}{6 a} = \frac{a^{2} + 5}{6 a} . \end{matrix}

(2)

P B C

háromszögből

\begin{matrix} a^{2} + 3^{2} - 6 a cos ψ = 4^{2}, \end{matrix}

ahonnan

\begin{matrix} cos ψ = \frac{a^{2} + 3^{2} - 4^{2}}{6 a} = \frac{a^{2} - 7}{6 a} . \end{matrix}

(3)

A (2) és (3) alatti értékeket (l)-be helyettesítve

\begin{matrix} {(\frac{a^{2} + 5}{6 a})}^{2} + {(\frac{a^{2} - 7}{6 a})}^{2} = 1, \end{matrix}

amiből

\begin{matrix} a^{4} - 20 a^{2} + 37 = 0. \end{matrix}

Ezzel az első megoldásban már szereplő egyenlethez jutottunk.

b) A négyzet megszerkesztése: Az

A

B

, ill.

C

pontok rendre a

P

pont körül

2

3

, ill.

4

egységnyi sugarú

k_{2}

k_{3}

k_{4}

körön lesznek (5. ábra). Az egyik csúcsot, pl.

A

-t tetszés szerint megválaszthatjuk a

k_{2}

körön. Képzeljük most megszerkesztettnek a négyzetet. A négyzet

B

csúcsát átvihetjük

C

-be úgy, hogy

A

körül

45^{\circ}

-kal elforgatjuk és egyidejűleg

A

-ból

1 : \sqrt[]{2}

arányban nyújtjuk. Hajtsuk végre ezt a transzformációt a

k_{3}

körre vonatkozóan, akkor a keletkezett új kör (

P'

körül

3 \sqrt[]{2}

sugarú) metszi ki a

k_{4}

körből a keresett négyzetnek

A

-val szemközt fekvő

C

(ill.

C^{*}

) csúcsát. Ennek ismeretében a másik két csúcspont már könnyen megkapható. Ismét csak egy esetben lesz

P

a négyzet belsejében.

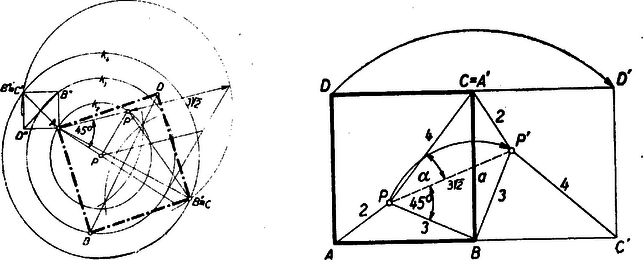5. ábra 6. ábra

IV. megoldás:
a) A négyzet megszerkesztése: Képzeljük a feladatot megoldottnak és forgassuk el a négyzetet a

B

csúcs körül

90^{\circ}

-kal úgy, hogy az

A

csúcs elforgatása:

A'

C

csúcsra kerüljön (6. ábra). A

P

elforgatása

P'

és a forgatás szöge miatt

P B P' ∢ = 90^{\circ}

és természetesen

P B = B P' = 3

.
Ezek alapján a szerkesztés menete: szerkesszünk egyenlőszárú derékszögű

P B P'

háromszöget

P B = B P' = 3

hosszúságú szárakkal (7. ábra) és szerkesszük meg azokat a pontokat, amelyek

P

-től

4

P'

-től

2

egység távolságra vannak.

2

megoldás:

C

és

C^{*}

. Ezek a pontok felelnek meg a

B

-vel szomszédos csúcsnak.

C

(ill.

C^{*}

) ismeretében a négyzet már könnyen megszerkeszthető. Ismét csak az egyik négyzet felel meg feltételünknek.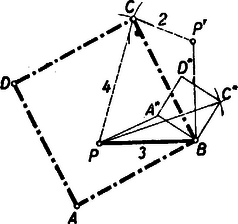

7. ábra

b) A terület kiszámítása: A szerkesztés módot ad a számítás elvégzésére is. A

B P C_{▵}

-ből (6. ábra) a cosinus-tétel szerint

\begin{matrix} a^{2} = B P^{2} + P C^{2} - 2 \cdot B P \cdot P C \cdot cos (45^{\circ} + α) = 3^{2} + 4^{2} - 24 (cos 45^{\circ} cos α - sin 45^{\circ} sin α) = \\ = 25 - 12 \sqrt[]{2} (cos α - sin α) . & (1) \end{matrix}

C P P'_{▵}

-ből

\begin{matrix} C P'^{2} = C P^{2} + P P'^{2} - 2 \cdot C P \cdot P P' cos α = 4^{2} + {(3 \sqrt[]{2})}^{2} - 24 \sqrt[]{2} cos α, \end{matrix}

ahonnan

\begin{matrix} cos α = \frac{16 + 18 - 4}{24 \sqrt[]{2}} = \frac{30}{24 \sqrt[]{2}} = \frac{5}{4 \sqrt[]{2}}, \end{matrix}

(2)

és így

\begin{matrix} sin α = \sqrt[]{1 - \frac{25}{32}} = \sqrt[]{\frac{7}{32}} = \frac{\sqrt[]{7}}{4 \sqrt[]{2}} . \end{matrix}

(3)

A (2) és (3) alatti értékeket (1)-be helyettesítve

\begin{matrix} a^{2} = 25 - 12 \sqrt[]{2} (\frac{5}{4 \sqrt[]{2}} - \frac{\sqrt[]{7}}{4 \sqrt[]{2}}) = 25 - 15 + 3 \sqrt[]{7} = 10 + 3 \sqrt[]{7} . \end{matrix}

(A szerkesztés második megoldása a

45^{\circ} - α

szögnek felel meg.)

Megjegyzés: A szerkesztés és a számítás is elvégezhető bármelyik bemutatott módon, akkor is, ha

2

3

4

helyett más

A P = p

B P = q

C P = r

távolság van adva.

A

és

C

szimmetrikus helyzete miatt feltehetjük, hogy

p \leq r

. Ez esetben az utolsó megoldásból pl. azonnal adódik, hogy a feladat akkor és csakis akkor oldható meg, ha

\begin{matrix} p + r \geq \sqrt[]{2} q és p + \sqrt[]{2} q \geq r, \end{matrix}

azaz

\begin{matrix} p \geq | \sqrt[]{2} q - r | . \end{matrix}

3. feladat.

I. megoldás: Azon

x

értékek jönnek csak számításba, amelyekre

\begin{matrix} 1 - sin 2 x \neq 0, vagyis x \neq \frac{π}{4} \pm k π (k = 0,1,2, ...) . \end{matrix}

Rendezve az egyenletet

\begin{matrix} (sin x + cos x) (1 - 2 sin x cos x) - cos^{2} x + sin^{2} x = 0, \end{matrix}

vagyis

\begin{matrix} sin x + cos x - 2 sin^{2} x cos x - 2 sin x cos^{2} x - cos^{2} x + sin^{2} x = 0 \end{matrix}

sin^{2} x

helyett mindenütt

1 - cos^{2} x

-et írva és rendezve

\begin{matrix} sin x - cos x + 2 cos^{3} x - 2 sin x cos^{2} x - 2 cos^{2} x + 1 = 0. \end{matrix}

A páratlan fokú tagokból

sin x

-et, ill.

cos x

-et kiemelve

\begin{matrix} sin x (1 - 2 cos^{2} x) + cos x (2 cos^{2} x - 1) - 2 cos^{2} x + 1 = 0 \end{matrix}

A baloldalon kiemelhető

2 cos^{2} x - 1

\begin{matrix} (2 cos^{2} x - 1) (cos x - sin x - 1) = 0. \end{matrix}

Innen vagy

\begin{matrix} 2 cos^{2} x - 1 = 0, \end{matrix}

(1)

vagy

\begin{matrix} cos x - sin x - 1 = 0. \end{matrix}

(2)

(1)-ből

\begin{matrix} cos x = \frac{1}{\sqrt[]{2}}, \end{matrix}

(3)

vagy

\begin{matrix} cos x = - \frac{1}{\sqrt[]{2}} . \end{matrix}

(4)

(2)-ből

\begin{matrix} cos x = 1 + sin x \end{matrix}

vagyis

\begin{matrix} cos^{2} x = 1 + 2 sin x + sin^{2} x, \end{matrix}

amiből (

cos^{2} x

helyébe

1 - sin^{2} x

-et írva és rendezve)

\begin{matrix} 2 sin^{2} x + 2 sin x = 2 sin x (sin x + 1) = 0 \end{matrix}

(5)

Egyelőre csak a főértékekre szorítkozva
(3)-ból

\begin{matrix} x = \frac{π}{4}, & (6) \\ x = \frac{7 π}{4}, & (7) \end{matrix}

(4)-ből

\begin{matrix} x = \frac{3 π}{4}, & (8) \\ x = \frac{5 π}{4}, & (9) \end{matrix}

(5)-ből

\begin{matrix} x = 0, & (10) \\ x = π, & (11) \\ x = \frac{3 π}{2} . & (12) \end{matrix}

Mivel nem mindig hajtottunk végre egyenértékű (ekvivalens) átalakításokat (pl. négyzetre emeltünk), azért meg kell vizsgálnunk, vajon a nyert gyökök kielégítik-e eredeti egyenletünket.
A (6) és (9) alatti gyökök éppen a kizárt értékek. Behelyettesítéssel meggyőződhetünk, hogy a (11) alatti gyök nem tesz eleget egyenletünknek, amíg a többi

4

gyök tényleg kielégíti egyenletünket.
Tehát a keresett gyökök főértékei

(0 \leq x < 2 π)

nagyságrendben:

\begin{matrix} x_{1} = 0 = 0^{\circ}, x_{2} = \frac{3 π}{4} = 135^{\circ}, x_{3} = \frac{3 π}{2} = 270^{\circ}, x_{4} = \frac{7 π}{4} = 315^{\circ} . \end{matrix}

Természetesen e főértékekhez

2 π = 360^{\circ}

többszöröseit hozzáadva vagy kivonva, ugyancsak gyököket nyerünk. Tehát az összes gyökök (

x_{2}

és

x_{4}

et egy képletbe összefoglalva):

\begin{matrix} x = & \pm 2 k π = \pm k \cdot 360^{\circ}, x = \frac{3 π}{4} \pm k π = 135^{\circ} \pm k \cdot 180^{\circ}, \\ x = \frac{3 π}{2} \pm 2 k π = 270^{\circ} \pm k \cdot 360^{\circ}, ahol k = 0,1,2, ... \end{matrix}

II. megoldás: Azok az

x

-ek jönnek csak tekintetbe, melyekre

\begin{matrix} 1 - sin 2 x \neq 0. \end{matrix}

(1)

Emeljük az egyenlet mindkét oldalát négyzetre, ekkor

\begin{matrix} {(sin x + cos x)}^{2} = sin^{2} x + 2 sin x cos x + cos^{2} x = 1 + sin 2 x \end{matrix}

folytán az egyenletben csak

2 x

szögfüggvényei fognak szerepelni. Az egyenletet

0

-ra redukálva és alkalmasan átalakítva:

\begin{matrix} (1 + sin 2 x) {(1 - sin 2 x)}^{2} - cos^{2} 2 x = (1 - sin^{2} 2 x) (1 - sin 2 x) - cos^{2} 2 x = \\ = (1 - sin^{2} 2 x) (1 - sin 2 x) - (1 - sin^{2} 2 x) = - sin 2 x (1 - sin^{2} 2 x) = \\ = - sin 2 x (1 + sin 2 x) (1 - sin 2 x) = 0 & (2) \end{matrix}

Itt (1) szerint az utolsó tényező nem lehet

0

, tehát csak a

\begin{matrix} sin 2 x = 0 és sin 2 x = - 1 \end{matrix}

egyenletek megoldásai jönnek számításba.
A

0 \leq x < 2 π

közben előbbi az

x = 0

\frac{π}{2}

π

\frac{3 π}{2}

értékekre, utóbbi pedig az

x = \frac{3 π}{4}

\frac{7 π}{4}

értékekre teljesül. Ezek közül az eredeti egyenletnek csak

\begin{matrix} x = 0, \frac{3 π}{2}, \frac{3 π}{4}, \frac{7 π}{4} \end{matrix}

értékek gyökei és természetesen minden olyan

x

érték, amely ezek valamelyikétől

\pm 2 k π

-vel különbözik, ahol

k = 1,2, ...

III. megoldás: Az átalakításokat kissé ügyesebben is végezhetjük: ha

\begin{matrix} cos x \neq sin x, azaz tg x \neq 1, x \neq \frac{π}{4} \pm k π, (k = 0,1,2, ...) \end{matrix}

akkor

\begin{matrix} sin x + cos x & = \frac{cos^{2} x - sin^{2} x}{1 - 2 sin x cos x} = \frac{(cos x - sin x) (cos x + sin x)}{cos^{2} x - 2 sin x cos x + sin^{2} x} = \frac{cos x + sin x}{cos x - sin x} . \end{matrix}

Rendezve az egyenletet

\begin{matrix} (sin x + cos x) (cos x - sin x - 1) = 0, \end{matrix}

tehát vagy

\begin{matrix} sin x + cos x = 0 \end{matrix}

(1)

vagy

\begin{matrix} cos x - sin x - 1 = 0 \end{matrix}

(2)

(1)-ből, mivel

cos x

és

sin x

nem tűnhet el egyszerre, s így az egyenlet megoldásaira egyik tag sem

0

\begin{matrix} tg x = - 1, x = - \frac{π}{4} \pm k π (k = 0,1,2, ...) . \end{matrix}

(2)-ből

\begin{matrix} 1 - cos x = - sin x, 2 sin^{2} \frac{x}{2} = - 2 sin \frac{x}{2} cos \frac{x}{2}, \\ 2 sin \frac{x}{2} (sin \frac{x}{2} + cos \frac{x}{2}) = 0. \end{matrix}

Itt vagy

\begin{matrix} sin \frac{x}{2} = 0, \frac{x}{2} = \pm k π (k = 0,1,2, ...), \end{matrix}

azaz

\begin{matrix} x = \pm 2 k π (k = 0,1,2, ...), \end{matrix}

vagy pedig

\begin{matrix} sin \frac{x}{2} + cos \frac{x}{2} = 0, \end{matrix}

amiből

\begin{matrix} tg \frac{x}{2} = - 1, \frac{x}{2} = - \frac{π}{4} \pm k π (k = 0,1,2, ...) \end{matrix}

azaz

\begin{matrix} x = - \frac{π}{2} \pm 2 k π (k = 0,1,2, ...) . \end{matrix}

A nyert értékek megoldást szolgáltatnak, mert ekvivalens átalakításokat végeztünk.

IV. megoldás: Induljunk ki a III. megoldásban nyert

\begin{matrix} sin x + cos x = \frac{sin x + cos x}{cos x - sin x} \end{matrix}

alakból.
Itt

\begin{matrix} sin x + cos x = \sqrt[]{2} \frac{\sqrt[]{2}}{2} sin x + \sqrt[]{2} \frac{\sqrt[]{2}}{2} cos x = \sqrt[]{2} (sin \frac{π}{4} cos x + cos \frac{π}{4} sin x) = \\ = \sqrt[]{2} \cdot sin (\frac{π}{4} + x), \end{matrix}

és

\begin{matrix} \frac{sin x + cos x}{cos x - sin x} = \frac{sin x cos \frac{π}{4} + cos x sin \frac{π}{4}}{cos x cos \frac{π}{4} + sin x sin \frac{π}{4}} = \frac{sin (\frac{π}{4} + x)}{cos (\frac{π}{4} + x)}, \end{matrix}

tehát az egyenlet

\begin{matrix} \sqrt[]{2} \cdot sin (\frac{π}{4} + x) = \frac{sin (\frac{π}{4} + x)}{cos (\frac{π}{4} + x)} . \end{matrix}

Írjunk

\frac{π}{4} + x = y

-t, ekkor

(mivel feltételeztük,hogy x \neq \frac{π}{4} \pm k π)

\begin{matrix} y \neq \frac{π}{2} \pm k π (k = 0,1,2, ...), azaz cos y \neq 0, \end{matrix}

és az egyenlet így alakul

\begin{matrix} sin y (\sqrt[]{2} cos y - 1) = 0, \end{matrix}

tehát vagy

\begin{matrix} sin y = 0, vagy cos y = \frac{1}{\sqrt[]{2}} . \end{matrix}

Az elsőből

\begin{matrix} y = \pm k π (k = 0,1,2, ...), \end{matrix}

a másodikból

\begin{matrix} y = \pm \frac{π}{4} \pm 2 k π (k = 0,1,2, ...), \end{matrix}

azaz

\begin{matrix} x = - \frac{π}{4} \pm k π, vagy x = \pm 2 k π, vagy x = - \frac{π}{2} \pm 2 k π, \end{matrix}

ahol

k = 0,1,2, ...

.
Minden átalakítás ekvivalens átalakítás volt, így mindezen értékek gyököket szolgáltatnak.