Cím: 1952. évi Kürschák József matematikai tanulóverseny
Szerző(k):  Hajós György 
Füzet: 1953/január, 1 - 12. oldal  PDF  |  MathML 
Témakör(ök): Kürschák József (korábban Eötvös Loránd)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A Bolyai János Matematikai Társulat 1952. október 18-án rendezte Budapesten, Debrecenben, Egerben, Győrött, Miskolcon, Pécsett, Sopronban, Szegeden, Szolnokon és Veszprémben, tehát egyidejűleg 10 helyen az 1952. évi Kürschák József matematikai tanulóversenyt. A versenyen 1952-ben érettségizettek és középiskolás diákok vehettek részt. A résztvevők és beadott dolgozatok száma: Budapesten 344 résztvevő 168 dolgozattal, Debrecenben 41 résztvevő 21 dolgozattal, Egerben 16 résztvevő 5 dolgozattal, Győrött 29 résztvevő 14 dolgozattal, Miskolcon 82 résztvevő 21 dolgozattal, Pécsett 31 résztvevő 6 dolgozattal, Sopronban 27 résztvevő 6 dolgozattal, Szegeden 35 résztvevő 13 dolgozattal, Szolnokon 57 résztvevő 38 dolgozattal, Veszprémben 51 résztvevő 17 dolgozattal, összesen tehát 713 résztvevő 309 dolgozattal. A verseny feladatai a következők voltak:
1. Három kör közül kettőnek-kettőnek nincs közös belső pontja, s középpontjaik egy egyenesen vannak. Bizonyítandó, hogy ha egy negyedik kör mindhármat érinti, akkor ennek sugara nem lehet a négy körsugár közül a legkisebb.
2. Az 1-től 3n-ig terjedő egész számok közül kiválasztunk n+2 darabot. Bizonyítandó, hogy mindig van a kiválasztott számok között kettő, melynek különbsége n-nél nagyobb, de 2n-nél kisebb.
3. Legyen a λ szám 12-nél nagyobb és 1-nél kisebb. Az ABC háromszög BC, CA és AB oldalára rendre felmérjük a

AB1=λ⋅BC,CB1=λ⋅CA,AC1=λ⋅AB
távolságot. Bizonyítandó, hogy az A1B1C1 háromszög kerülete az ABC háromszög kerületének λ-szorosánál kisebb.
A Bolyai János Matematikai Társulat elnöksége által kiküldött versenybizottság, melynek tagjai Gallai Tibor, Kárteszi Ferenc, Surányi János, Vincze István és Hajós György előadó, 1952. november 20-án tartott ülésén egyhangúan a következő jelentést fogadta el:
,,A versenyen résztvevőknek s a beadott dolgozatoknak száma több mint 50%-kal haladta meg az eddig legnépesebb múlt évi verseny megfelelő adatait. A bizottság örömmel állapítja meg ebből a matematikai tanulóversenyek iránti érdeklődés fokozódását.
Legkönnyebbnek az első feladat bizonyult, a másik két feladatra csak nagyon kevés jó megoldást adtak be a versenyzők. A második feladat szövegezése nem kifogástalan: a feladat szövegéből kimaradt, hogy a szereplő n egész szám 1-nél nagyobb. Ez a körülmény azonban a verseny során zavart nem okozott.
Kiemelkedik a beadott dolgozatok közül Kálmán Lajos és Kántor Sándor dolgozata. Kálmán Lajos a múlt tanévben a budapesti V. ker. Berzsenyi Dániel gimnáziumban érettségizett, Somosi Ferenc tanár tanítványa. Azzal emelkedik ki valamennyi versenyző közül, hogy egyedül az ő dolgozata tartalmazza két feladatnak hiánytalan megoldását. Az általa meg nem oldott második feladatnál is jól indul el, azonban okoskodását hibásan fejezi be. Kántor Sándor a debreceni református gimnáziumban a múlt tanévben a III. osztályt végezte, Nagy Géza tanár tanítványa. Dolgozata kiemelkedik logikus és tömör fogalmazásával. Az első feladatra két szép megoldást ad, a második feladat megoldásának leírását csak egy kis kihagyás zavarja. A harmadik feladattal nem foglalkozott. A bizottság az 1952. évi első Kürschák József-díjat megosztva Kálmán Lajosnak és Kántor Sándornak ítéli, s dolgozataikat 300-300 forinttal jutalmazza.
Második helyen Horváth Ákos és Nagy Tibor dolgozatát kell kiemelnünk. Horváth Ákos a múlt évben érettségizett a szentendrei ferences gimnáziumban, Vigh Árpád tanár tanítványa. Az első feladat hiánytalan megoldása mellett lényegében a második feladatot is megoldotta. Ez utóbbinál azonban okoskodása nem foglalkozik minden esettel, viszont elintézi azt az esetet, amelyik egyedül okoz komoly nehézséget. A harmadik feladattal nem foglalkozott. Nagy Tibor a múlt évben érettségizett a váci Sztáron Sándor gimnáziumban, Gyaraki Ferenc tanár tanítványa. Az első és harmadik feladatot oldotta meg, az elsőnél azonban a lehetséges esetek taglalása hiányos. A második feladatra beadott megoldása hibás. A bizottság az 1952. évi második Kürschák József-díjat megosztva Horváth Ákosnak és Nagy Tibornak ítéli, s munkájukat 200-200 forinttal jutalmazza.
A többi dolgozat lényegében helyesen is csak legfeljebb egy feladatnak megoldását tartalmazza.''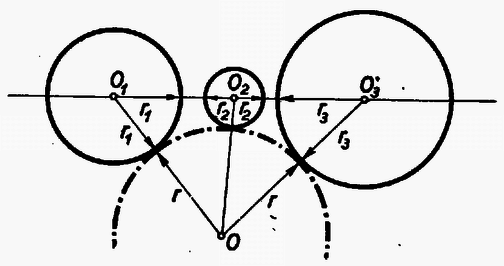
 
A verseny eredményének kihirdetésére Budapesten a Bolyai János Matematikai Társulat 1952. november 15-én tartott ülésén került sor. Ezen az ülésen a versenybizottság előadója ismertette a feladatok megoldásait. Az alábbiakban e megoldásokat közöljük.
 
1. feladat.
 
I. megoldás: Jelölje O1, O2, O3 a három adott kör középpontját, s legyen közülük O2 a másik kettő között. A három kör sugarát rendre r1, r2, r3 jelöli. A negyedik kör középpontja és sugara legyen O és r.
 
 
1. ábra
 

A negyedik kör nem lehet egyik adott körnek sem a belsejében, mert akkor nem érinthetné a másik kettőt is. Nem kell foglalkoznunk avval az esettel sem, midőn a három adott körnek valamelyike a negyedik kört belülről érinti, mert ez esetben a negyedik kör sugara a belülről érintő kör sugaránál nagyobb, s így nem lehet a négy körsugár közül a legkisebb. Ezért csak avval az esettel foglalkozunk, amikor a negyedik kör kívülről érinti a három adott kört (1. ábra).
Az OO1O3Δ old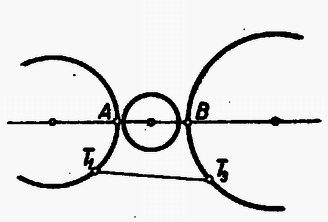alaira
OO1+OO3>O1O3.
Minthogy a körök kívülről érintik egymást, OO1=r+r1 és OO3=r+r3. Mivel a három adott kör közül nincs kettőnek közös belső pontja, O1O3≥r1+2r2+r3, hiszen az O1O3 szakasz tartalmazza a két szélső kör sugarát s a középsőnek átmérőjét, s e sugarak és az átmérő egymást még részben sem fedik. Igaz ez akkor is, ha a középső kör érinti a két szélsőnek valamelyikét, vagy akár mindkettőt is. Az utóbbi esetben az egyenlőség jele érvényes.
 
Fenti egyenlőtlenségünk alapján tehát
r1+2r+r3>r1+2r2+r3,
amiből r>r2 adódik. Az r sugár tehát r1, r2, r3 mindegyikénél kisebb nem lehet.
 
II. megoldás: Jelölje A és B a két szélső körnek egymáshoz legközelebb eső pontjait, tehát a centrális egyenesnek s a két szélső körnek egy-egy metszéspontját (2. ábra).
 
 
2. ábra
 

Minthogy az AB távolság a középső kör átmérőjét tartalmazza,
AB≥2r2.

Jelölje T1 és T3 a negyedik körnek s a két szélső körnek közös pontjait. Minthogy T1T3 a negyedik körnek húrja,
2r≥T1T3.
A és B megválasztásából viszont következik, hogy
T1T3≥AB.

Egyenlőtlenségeink összevetéséből
2r≥2r2,
azaz r≥r2 adódik. Ez pedig a feladat állítását igazolja.
 

III. megoldás: Emeljünk a centrális egyenesnek s a középső körnek metszéspontjaiban merőlegeseket a centrálisra (3. ábra).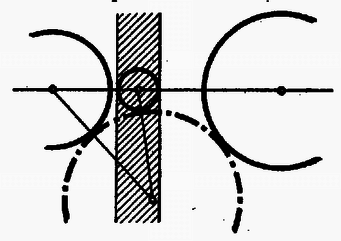
 
 
3. ábra
 

E két párhuzamos egyenes egy síksávot fog közre. A három adott kör közül a két szélső ennek a sávnak más-más oldalán van. Minthogy a negyedik körnek van közös pontja mindkét szélső körrel, azért tudjuk, hogy a negyedik kör a sávnak mindkét partját eléri, átmérője tehát a sáv szélességénél, sugara pedig annak felénél, vagyis a középső kör sugaránál kisebb nem lehet.
 

IV. megoldás: Keressük az olyan negyedik körnek középpontját, amelyiknek van a két szélső körrel egy-egy közös pontja, s amelyiknek sugara a középső kör sugaránál kisebb.
Ha a két szélső kör sugarát a középső kör sugarával megnöveljük, olyan köröket kapunk, amelyeknek mindegyike belsejében kell, hogy tartalmazza a kívánt tulajdonságú negyedik körnek középpontját (4. ábra).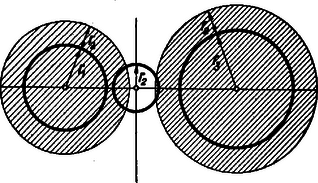
 
 
4. ábra
 

Hiszen e körök valamelyikén kívül lévő pont körül r2-nél kisebb sugárral írt kör nem éri a megfelelő szélső kört.
Emeljünk a középső kör középpontjában merőlegest a centrális egyenesre. Minthogy éppen a középső kör sugarával növeltük az előbb a sugarakat, azért a megnövelt körök a most szerkesztett merőleges egyenesnek más-más oldalán vannak. A megnövelt köröknek tehát nincs közös belső pontjuk, s így kívánt tulajdonságú negyedik kör sincs.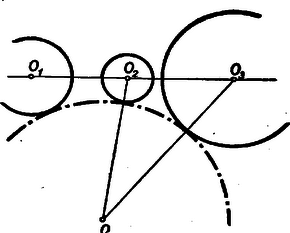
 
V. megoldás: Kössük össze a negyedik kör O középpontját a középső kör O2 középpontjával. Az OO2O1∢ és OO2O3∢ összege 180∘, s így mindkettő nem lehet 90∘-nál kisebb (5. ábra).
 
 
5. ábra
 

Legyen pl. OO2O3∢≥90∘. Ekkor az OO2O3Δ-ben ez a legnagyobb szög, s ezért OO3 a háromszög legnagyobb oldala, tehát
OO3>O2O3.
Minthogy az O és O3 középpontú köröknek van közös pontjuk, OO3≤r+r3. Mivel az O2 és O3 középpontú köröknek nincs közös belső pontjuk, O2O3≥r2+r3. Így tehát
r+r3>r2+r3,
azaz r>r2, tehát r nem lehet r1, r2, r3 mindegyikénél kisebb.
 
Megjegyzések: 1. Végső következtetésünk mindegyik megoldásnál az volt, hogy r nem lehet a legkisebb a négy körsugár közül, azaz nem lehet a másik három mindegyikénél kisebb. Megoldásaink azt is bizonyítják, hogy r nem lehet r2-nél kisebb sem.
2. Az is igaz, hogy r nem lehet a négy körsugár közül még a legkisebbek között sem, azaz van a másik három sugár között r-nél kisebb. Sőt bizonyos, hogy r2 kisebb r-nél. Ezt az első és ötödik megoldás ki is mondja. A többi három megoldás okoskodása csekély toldással ugyancsak elvezet ehhez az eredményhez.
3. Az első megoldás használta csak ki azt, hogy a negyedik kör érinti a két szélsőt. A többi arra épített, hogy a negyedik körnek van közös pontja a szélső körökkel, tehát azt is megengedte, hogy a negyedik kör messe a szélsőket. Az első megoldás lényegtelen módosítással ugyanilyenné alakítható.
4. Csak az első és ötödik megoldás használta ki valamennyire azt, hogy a negyedik kör érinti a középsőt. Ez abban nyilvánult, hogy e megoldások OO1O3, ill. OO2O3 háromszögről szóltak, tehát feltételezték hogy O nincs rajt a centrális egyenesen. Ez valóban nem következhetik be, ha a negyedik körnek van közös pontja a szélső körökkel, és érinti a középsőt. Így érthető az is, hogy éppen ezt a két megoldást kellett 2. megjegyzésünkben kiemelnünk.
5. A második megoldásból kiolvashatjuk, hogy r=r2 csak akkor állhat fenn, ha mindenütt az egyenlőség jele volt érvényes: ha tehát AB átmérője a középső körnek, ha T1T3 átmérője a negyedik körnek, ha továbbá T1T3 és AB azonos. Ez pedig azt jelenti, hogy a középső kör érinti a két szélsőt, és a negyedik körrel azonos. Ugyanehhez az eredményhez a többi megoldás alapján is eljuthatunk.
6. Megjegyzéseinket összefoglalva a feladat állításának következő általánosítását mondhatjuk ki: Három kör közül kettőnek-kettőnek nincs közös belső pontja, s középpontjaik egy egyenesen vannak; ha egy negyedik körnek van közös pontja e három kör közül a két szélsőnek mindegyikével, akkor e negyedik körnek sugara nem lehet a középső kör sugaránál kisebb, és egyenlő is csak akkor lehet azzal, ha a középső kör érinti a két szélsőt, s ha továbbá a negyedik kör a középső körrel azonos.
 
2. feladat.
 
I. megoldás: Az első 3n egész számot három csoportba osztjuk:
A) 1,2,...,n;
B) n+1,n+2,...,2n;
C) 2n+1,2n+2,...,3n.
Minthogy n+2 számot választunk ki, ezeket mind nem választhatjuk egyetlen csoportból.
Ha a számokat csak az A és B, vagy pedig csak a B és C csoportokból választjuk, akkor a kiválasztott számok legkisebbikének és legnagyobbikának különbsége n-nél nagyobb, hiszen közöttük van a többi n kiválasztott szám, viszont 2n-nél kisebb, hiszen a csoportok legszélső elemeinek különbsége is csak 2n-1.
Ha a számokat az A és C csoportból választjuk, akkor az A csoportból kiválasztott legnagyobb s a C csoportból kiválasztott legkisebb számnak különbsége n-nél nagyobb, hiszen e két csoport legközelebbi elemeinek különbsége is n+1. Ugyanannak a két kiválasztott számnak a különbsége azonban 2n-nél kisebb is, mert közöttük csak ki nem választott számok vannak, s valamennyi ki nem választottnak száma is csak 3n-(n+2)=2n-2.
Foglalkozzunk végül avval az esettel, amikor mindhárom csoportból választjuk a számokat. Legyenek a, b, c rendre az A, B, C csoportba tartozó kiválasztott számok. Feltehetjük, hogy a b-a és c-b különbségeknek nem mindegyike n, hiszen ellenkező esetben az a, b, c számok valamelyike helyett egy ugyanabba a csoportba tartozó másik kiválasztott számot tekinthetnénk. Ez lehetséges, mert n>1 feltevés mellett n+2>3, tehát valamelyik csoportból több számnak kell szerepelnie a kiválasztottak között.
Nem kell foglalkoznunk avval az esettel sem, amidőn a b-a és c-b különbségeknek valamelyike n-nél nagyobb, hiszen e különbségek 2n-nél kisebbek, minthogy az A és B, valamint a B és C csoportok legtávolabbi elemeinek különbsége is csak 2n-1.
Így csak annak az esetnek vizsgálata marad hátra, amidőn a b-a és c-b különbségeknek egyike sem nagyobb n-nél, de legalább az egyike kisebb. Ebben az esetben azonban c-a, mint e különbségeknek összege, 2n-nél kisebb, s másrészt eleve n-nél nagyobb, hiszen a B csoportnak mind az n eleme a és c között van.
Olyan utasítást adtunk tehát, amely minden esetben elvezet egy kívánt tulajdonságú számpárhoz.
 
II. megoldás: Két kiválasztott számot szomszédosnak mondunk, ha a közöttük lévő számoknak egyike sem szerepel a kiválasztottak között. Két szomszédos kiválasztott számnak különbsége nem lehet 2n vagy még több, mert szomszédos kiválasztott számok között ki nem választott számok vannak, és csak 3n-(n+2)=2n-2 ki nem választott szám van. Ha a kiválasztott számok közül két szomszédosnak különbsége 2n-nél kisebb, de n-nél nagyobb, akkor e két szám a feladat kívánalmát kielégíti. Így tehát csak azzal az esettel kell foglalkoznunk, amikor a kiválasztott számok közül bármely két szomszédosnak különbsége legfeljebb n.
Legyen a a kiválasztott számok legkisebbike. Ha szerepel a kiválasztott számok között olyan, amelyik (a+n)-nél nagyobb s (a+2n)-nél kisebb, akkor a és ez a szám kielégíti a feladat kívánalmát. Ha viszont a mondott számoknak egyike sem szerepel a kiválasztottak között, akkor a+n és a+2n szükségképpen szerepel közöttük, mert különben a mondott számokat közrefogó két szomszédos kiválasztott számnak különbsége feltevésünkkel ellentétben n-nél nagyobb volna. Bizonyos, hogy van két ilyen közrefogó szomszédos szám, hiszen maga a a mondott számoknál kisebb, s nagyobbnak is kell lennie a kiválasztott számok között, minthogy a-tól kezdve (a+n)-ig bezárólag összesen csak n+1 szám van.
Ha viszont a, a+n és a+2n szerepel a kiválasztott számok között, akkor bármely negyedik szám e három valamelyikével együtt megfelel a feladat kívánalmának. Hiszen a-nál kisebb szám nincs a kiválasztottak között, az a-nál nagyobb és (a+n)-nél kisebb számoknak (a+2n)-nel alkotott különbségük, az (a+n)-nél nagyobb és (a+2n)-nél kisebb számoknak a-val alkotott különbségük, az (a+2n)-nél nagyobb és 3n-nél nem nagyobb számoknak pedig (a+n)-nel alkotott különbségük n-nél nagyobb s egyben 2n-nél kisebb. Minthogy pedig n>1 esetben n+2>3, található a felsorolt háromtól különböző negyedik kiválasztott szám. Így tehát minden esetben eljutottunk a feladat kívánalmát kielégítő számpárhoz.
 
III. megoldás: Ha a kiválasztott számok között 3n nem szerepel, akkor mindegyik kiválasztott számot megnövelhetjük ugyanannyival úgy, hogy 3n legyen a kapott számok legnagyobbika. Minthogy e növelés a számok különbségeit nem változtatja meg, elegendő avval az esettel foglalkoznunk, midőn 3n szerepel a kiválasztott számok között. E feltevés mellett a következőképpen okoskodunk:
Ha az n+1, n+2,...,2n-1 számok egyike szerepel a kiválasztottak között, úgy ennek és 3n-nek különbsége n-nél nagyobb, de 2n-nél kisebb.
Ha viszont a mondott számok egyike sem szerepel, akkor az
1,2n;2,2n+1;3,2n+2;...;n,3n-1
számpárok elemei közül kell további n+1 darabot kiválasztanunk. E kiválasztás csak úgy lehetséges, hogy valamelyik számpárnak mindkét elemét kiválasztjuk, hiszen összesen csak n számpár van. Így tehát van a kiválasztott számok között kettő, melyeknek különbsége 2n-1, vagyis 2n-nél kisebb s egyben n-nél nagyobb, hiszen n>1 feltevés mellett n<2n-1.
 
IV. megoldás: Helyezzük el az első 3n természetes számot egy kör kerületén növekvő rendben s egyenlő közökben. Az óralap szemlélteti ezt az elhelyezést az n=4 esetben.
Két szám akkor elégíti ki a feladat kívánalmát, ha a kisebbiktől növekvő számok irányában haladó, s a nagyobbikhoz vezető körívnek hossza harmadkörnél nagyobb s a kör kétharmadánál kisebb. Ez a megkötés azonban egy körívre s az azt teljes körré kiegészítő körívre csak egyszerre teljesülhet, és ha két egymást teljes körré kiegészítő körívnek mindegyike nagyobb a harmadkörnél, akkor már eleve kisebbek a kör kétharmadánál. Így tehát két szám akkor elégíti ki a feladat kívánalmát, ha a két számot összekötő mindkét körív nagyobb a harmadkörnél.
Meggondolásaink alapján a feladatnak a következő új alakot adhatjuk: Egy kör kerületén egyenlő közökkel 3n pont helyezkedik el, s ezek közül kiválasztunk n+2 darabot. Bizonyítandó, hogy mindig van a kiválasztott pontok között kettő, melyeket két, a harmadkörnél nagyobb körív köt össze.
Vizsgáljuk, hogyan lehet a 3n pont közül egyeseket kiválasztani anélkül, hogy volna közöttük kettő, melyeket két, a harmadkörnél hosszabb körív köt össze. Ez a tilalom akként is szövegezhető, hogy a kiválasztott pontokkal szemben elhelyezkedő harmadkörívek belsejéből nem szabad pontot kiválasztanunk.
 
Nevezzük szabad körívnek az olyat, amelyet kiválasztott pontok határolnak, s amelyiknek belsejében nincs kiválasztott pont. A tilalom előbbi megfogalmazása szerint kell lennie legalább harmadkör-hosszúságú szabad körívnek. Viszont ugyancsak a tilalom szerint nem szabad harmadkörnél hosszabb s a kör kétharmadánál rövidebb szabad körívnek lennie, hiszen egy ilyennek végpontjai áthágják a tilalmat. Megengedett kiválasztásoknál tehát csak a következő két eset lehetséges: a szabad körívek maximuma vagy éppen harmadkörív, vagy pedig a kör két harmadát is eléri.
Ha a legnagyobb szabad körív harmadkör, akkor csak 3 kiválasztott pont szerepelhet (6. ábra).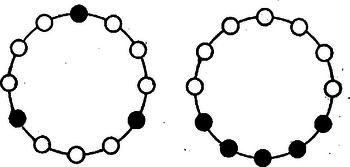
 
 
6. ábra
 

Ilyenkor ugyanis bizonyosan van egy szabad harmadkörív. Ennek végpontjai, mint kiválasztott pontok, a kiegészítő kétharmadív belső pontjainak kiválasztását is tiltják, egyedül e kétharmadív középpontjának kiválasztását nem. Ennek a középpontnak kell is szerepelnie a kiválasztott pontok között, mert különben nem harmadkör volna a szabad körívek legnagyobbika.
Ha viszont a legnagyobb szabad körív a körnek kétharmada, vagy még nagyobb, akkor a kiválasztott pontok egy harmadkörön helyezkednek el, ennek végpontjait is beleértve. Minthogy egy harmadköríven végpontjaival együtt n+1 pont van, ilyenkor legfeljebb csak n+1 kiválasztott pont szerepelhet. Akár mind e pontokat kiválaszthatjuk, a tilalmat akkor sem hágjuk át.
Mivel n+2 nagyobb (n+1)-nél és n>1 feltevés mellett 3-nál is, azért n+2 pontot nem lehet a tilalom áthágása nélkül kiválasztani.
 
Megjegyzés: Könnyű előző megoldásainkat is átfogalmazni körön elhelyezkedő számokra. Ezáltal azoknak tartalma is szemléletesebbé válik. Ezt azonban az olvasóra hagyjuk.
Megoldásunk a feladat állításán túlmenően a következő eredményhez is elvezet: Minden megengedett kiválasztásnál: 1) vagy három a, a+n, a+2n alakú szám szerepel, 2) vagy n+1 egymást követő szám szerepel, 3) vagy együttesen n+1 olyan szám szerepel, amelyeknek egyik csoportja 1-hez csatlakozó s egymást követő, másik csoportja 3n-hez csatlakozó s egymást követő számokat tartalmaz, 4) vagy pedig csak egyesek szerepelnek az előző két eset valamelyikében megadott számok közül.
 
V. megoldás: A feladatnak n=60 esetben a következő tréfás fogalmazást adhatjuk: Egy könyvtárt déli 12-kor nyitnak és délután 3 órakor becsuknak. A könyvtárba csak pontosan kerek percidőkkor lehet belépni: első ízben pontosan 12-kor, utóljára 2 óra 59 perckor. Egyszerre csak egy ember léphet a könyvtárba. Aki a könyvtárba lép, belépése után pontosan egy órával elalszik s pontosan egy órát alszik, hacsak a könyvtár zárása ebben meg nem akadályozza. Senkit alvás közben a könyvtárba lépéssel zavarni nem szabad. Bizonyítandó, hogy ilyen különös előírások mellett egy napon nem járhat 62 ember a könyvtárban.
Felesleges volna részletezni, hogy ez valóban a feladat átírása.
Ha a könyvtár kapusa az első látogató érkezésekor a könyvtár óráját déli 12-re állítja vissza, akkor nyilván csak azt teszi lehetővé, hogy esetleg még többen látogathassák aznap a könyvtárt. Feltehetjük tehát, hogy az első látogató pontosan 12-kor érkezik. A következőkben három esetet különböztetünk meg.
Először avval az esettel foglalkozunk, hogy pontosan 1 órakor és pontosan 2 órakor is érkezik egy-egy látogató. Ekkor bizonyos, hogy többen nem is járnak a könyvtárban. Hiszen 12 és 1 között nem érkezhetik senki sem, mert az 2-kor biztosan aludna, s így álmát megzavarnák. Viszont 1 és 2, valamint 2 és 3 között azért nem jöhet be senki sem, mert akkor alszik a 12-kor érkező, ill. az 1-kor érkező látogató. Ebben az esetben tehát 3 látogató van.
Másodszor feltesszük, hogy pontosan 1 órakor érkezik látogató, de 2-kor nem. Ekkor bizonyos, hogy 1 óra után senki sem érkezik. Ugyanis 1 és 2 között a 12-kor érkező, viszont 2 és 3 között az 1-kor érkező látogató alszik. Ebben az esetben tehát minden látogató 12-től kezdve 1 óráig bezárólag érkezik, s így legfeljebb 61 látogató van.
Végül harmadszor feltesszük hogy pontosan 1 órakor nem érkezik látogató. Szemeljük ki ekkor azt a látogatót, aki utoljára érkezett 1 óra előtt (lehet, hogy az első látogatót kell így kiszemelnünk). A kiszemelt látogató érkezésétől számított kétórás időközön belül újabb látogató nem érkezhet, hiszen ez csak elalvása előtt volna lehetséges, viszont sem érkezésétől 1 óráig, sem 1 órakor nem érkezik senki sem, és 1 órától a kiszemelt látogató elalvásáig terjedő időben (ha ugyan nem az első látogatót magát szemeltük ki), már alszik az első látogató. Ezek szerint a mondott két órás időközön belül 119 belépési lehetőség kihasználatlanul kell, hogy maradjon, a látogatók a megengedett 180 lehetőségből csak a többit használhatták ki. Ebben az esetben tehát ugyancsak legfeljebb 61 látogató van. Egybevetve megállapítjuk, hogy mindenképpen csak legfeljebb 61 ember járhat egy napon a könyvtárban. Nyilván helyes marad okoskodásunk akkor is, ha az órát nem 60, hanem n percre osztjuk fel. Egyedül az lényeges, hogy a 61 helyébe lépő n+1 ne legyen 3-nál kisebb, vagyis hogy az n>1 feltétel teljesüljön.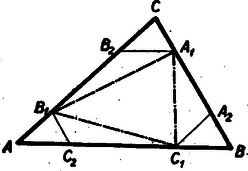
 
3. feladat.
 
I. megoldás: Húzzunk párhuzamosakat az A1, B1, C1 pontokon át rendre az AB, BC, CA oldalakkal (7. ábra). E párhuzamosak a CA, AB, BC oldalakat rendre B2, C2, A2 pontokban metszik. Az így kapott AC2B1, C1BA2, B2A1C háromszögek oldalaik párhuzamossága miatt hasonlók az ABCΔ-höz.
 
 
7. ábra
 

E háromszögek egymással egybevágók, ugyanis
A1C=(1-λ)⋅BC,B1A=(1-λ)⋅CA,C1B=(1-λ)⋅AB
miatt egy-egy oldaluk az eredeti háromszög megfelelő oldalának ugyanannyiszorosa. Az egybevágóságból következik, hogy
A1B2=C2A,B1C2=A2B,C1A2=B2C.
Ebből pedig az adódik, hogy az A1B2B1C2C1A2 hatszög kerülete az AC1, BA1, CB1 távolságok összegével, vagyis az eredeti háromszög oldalai λ-szorosainak összegével, tehát az ABCΔ kerületének λ-szorosával egyenlő.
A feladat állítása most már abból következik, hogy az A1B1C1Δ kerülete a szerepeltetett hatszög kerületénél kisebb. Hiszen e háromszög egy-egy oldala kisebb a hatszög két-két oldalának összegénél.
 
Megjegyzés: Megoldásunk kihasználta, hogy a szereplő hatszög csúcsai mind különböző pontok. Ez nem következik be, ha λ=12, amikor is A1≡A2, B1≡B2, C1≡C2, s akkor sem, ha λ=1, amikor viszont A1≡B2, B1≡C2, C1≡A2. A feladat állítása sem helyes ebben a két esetben, hiszen az A1B1C1Δ kerülete mindkét esetben éppen egyenlő az ABCΔ kerületének λ-szorosával.
Kihasználta okoskodásunk azt a tényt is, hogy a C2, A2, B2 pontok rendre az AC1, BA1, CB1 távolságok belsejében vannak. Hiszen különben nem volna pl. a hatszög A1B2 és C2C1 oldalának összege az AC1 távolsággal egyenlő. A mondott tény bekövetkezése annak következménye, hogy λ>12, azaz 1-λ<λ. Ugyanis pl.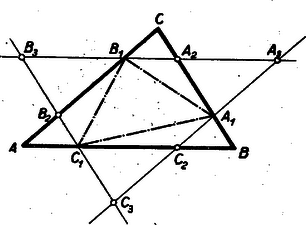
AC2=(1-λ)⋅AB<λ⋅AB=AC1.
Nem is igaz a feladat állítása, ha 0<λ<12. Ezt a következőképpen bizonyítjuk: Az A1, B1, C1 pontokon át párhuzamosakat húzunk rendre a CA, AB, BC oldalakkal (8. ábra).
 
 
8. ábra
 

E párhuzamosak az AB, BC, CA oldalakat rendre C2, A2, B2 pontokban metszik, s együttesen az A3B3C3Δ-et határolják. Az AC1B2, C2BA1, B1A2C háromszögek oldalaik párhuzamossága miatt hasonlók az eredeti háromszöghöz, s egymással egybevágók is, mert mindegyiküknek egy-egy oldala az ABCΔ megfelelő oldalának λ-szorosa. Így tehát
B1A2=λ⋅AB,C1B2=λ⋅BC,A1C2=λ⋅CA.

Tudjuk most azt is, hogy az A2, B2, C2 pontok rendre a BA1, CB1, AC1 távolságokon kívül vannak, hogy tehát az A3B3C3Δ csúcsai az eredeti háromszögön kívül helyezkednek el. Az előbbi mintára belátjuk, hogy az A3A2A1, B1B3B2, C2C1C3 háromszögek hasonlók az eredeti háromszöghöz, s egymással egybevágók, mert A1A2, B1B2, C1C2 oldalaik az ABCΔ megfelelő oldalainak (1-2λ)-szorosai. Így tehát
A2A3=B3B1,B2B3=C3C1,C2C3=A3A1.
Az A1B1A3, B1C1B3, C1A1C3 háromszögek egy-egy oldalára felírva, hogy a másik két oldal különbségénél nagyobb:
A1B1>B1A2+A2A3-A3A1,B1C1>C1B2+B2B3-B3B1,C1A1>A1C2+C2C3-C3C1.


Ezeknek az egyenlőtlenségeknek összege a fenti egyenlőségek figyelembe vételével:
A1B1+B1C1+C1A1>B1A2+C1B2+A1C2.
Ez pedig fentebbi megállapításunk értelmében éppen azt mondja ki, hogy az A1B1C1Δ kerülete az ABCΔ kerületének λ-szorosánál nagyobb.
Akkor sem teljesül a feladat állítása, ha λ>1, mikor is az A1, B1, C1 pontok az ABCΔ oldalainak meghosszabbítására kerülnek. Ezt a következőképpen látjuk be: Az A1, B1 C1 pontokon át párhuzamosakat húzunk rendre az AB, BC, CA oldalakkal (9. ábra).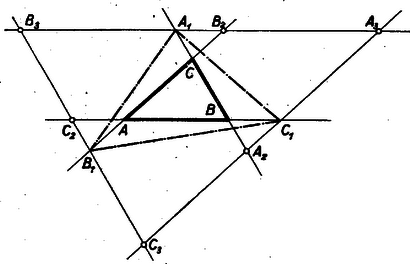
 
 
9. ábra
 

E párhuzamosak a CA, AB, BC oldalakat rendre B2, C2, A2 pontokban metszik, s együttesen az A3B3C3Δ-et határolják. Az AC2B1, C1BA2, B2A1C háromszögek oldalaik párhuzamossága miatt hasonlók az eredeti háromszöghöz, s egymással egybevágók, mert egy-egy oldaluk az ABCΔ megfelelő oldalának (λ-1)-szerese. Ebből az egybevágóságból következik, hogy A2B=CA1, B2C=AB1, C2A=BC1, hogy tehát a CA2, AB2, BC2 távolságok is λ-szorosai az ABCΔ oldalainak. Minthogy AB2A3C1, BC2B3A1 és CA2C3B1 paralelogramma, megállapításainkból következik, hogy az A3B3C3Δ oldalait az ezeken elhelyezkedő két-két pont olyan három‐három távolságra darabolja, amelyek az ABCΔ egy-egy oldalának sorjában λ-szorosai, (λ-1)-szeresei és λ-szorosai. Így tehát az A1B1C1Δ csúcsai úgy helyezkednek el az A3B3C3Δ oldalain, hogy
B3A1:B3A3=C3B1:C3B3=A3C1:A3C3,
hiszen ezeknek az arányoknak mindegyike a λ:(3λ-1) aránnyal egyenlő. Minthogy ennek az aránynak értéke λ>1 folytán 12-nél kisebb, azért előzőleg bizonyított állításunk e háromszögekre teljesül. Tudjuk tehát, hogy az A1B1C1Δ kerülete nagyobb a B3A1, C3B1, A3C1 távolságok összegénél, azaz az ABCΔ kerületének λ-szorosánál.
Megjegyezhetjük még, hogy λ≤0 esetben a feladat állítása eleve nem teljesülhet, hiszen egy háromszög kerülete csak pozitív lehet.
Összefoglalva az e megjegyzésben mondottakat megállapítjuk, hogy a feladat 1/2<λ<1 megkötése lényeges. Ha e megkötés nem teljesül, a feladat állítása soha sem helyes.
 
II. megoldás: Ha a γ1 és γ2 szög 0-nál nagyobb és 180∘-nál kisebb, akkor
sin(γ1+γ2)<sinγ1+sinγ2,
hiszen a baloldalt növeljük, ha azt sinγ1cosγ2+cosγ1sinγ2 alakban írva a pozitív sinus-tényezők cosinus-együtthatóinak helyébe azoknál nagyobb 1-et írunk.
Ha továbbá egy ugyancsak 0-nál nagyobb és 180∘-nál kisebb δ szöget szerepeltetünk, akkor az előző egyenlőtlenséget a pozitív sinδ-val szorozva
sin(δ+γ1)sinγ2+sin(δ-γ2)sinγ1<sinδ(sinγ1+sinγ2)
adódik. Ugyanis (a szereplő szögösszegek és szögkülönbségek függvényeit a tagok függvényeivel fejezve ki)
sinδsin(γ1+γ2)=sin(δ+γ1)sinγ2+sin(δ-γ2)sinγ1
azonosan teljesül. Így tehát utolsó egyenlőtlenségünket a pozitív sinγ1sinγ2 szorzattal osztva
sin(δ+γ1)sinγ1+sin(δ-γ2)sinγ2<sinδsinγ1+sinδsinγ2.

Tekintsünk egy a, b, c oldalú háromszöget, melyet egy d hosszúságú távolság egy a, d, c1 és egy b, d, c2 oldalú háromszögre vág (10. ábra).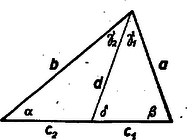
 
 
10. ábra
 

Ezekre fennáll a
dc1+dc2<ac1+bc2
egyenlőtlenség. Ugyanis a sinus-tétel szerint ez az előbbi egyenlőtlenséggel azonos, ha ábránk szögjelöléseit használjuk, hiszen e szögekre
a=δ-γ2,β=π-(δ+γ1).
Ha utolsó egyenlőtlenségünket (1c1+1c2)-vel osztjuk és a μ=c1c1+c2 jelölést használjuk, akkor a
d<μb+(1-μ)a
egyenlőtlenséghez jutunk.
Tekintsünk egy A2B2C2Δ-et (11. ábra), melynek oldalain az A3, B3, C3 pontok úgy helyezkednek el, hogy
A3C2:B2C2=B3A2:C2A2=C3B2:A2B2.
 
11. ábra
 

Állítjuk, hogy az A2A3, B2B3, C2C3 távolságok összege az A3B3C3 kerületénél kisebb. Ha ugyanis a fenti arányok közös értékét μ-vel jelöljük, akkor előző megállapításunk értelmében
A2A3<μA2B2+(1-μ)C2A2,B2B3<μB2C2+(1-μ)A2B2,C2C3<μC2A2+(1-μ)B2C2.



Ezeknek az egyenlőtlenségeknek összege éppen állításunkat adja.
Tekintsük végül magát a feladatban leírt alakzatot. Legyen az A2B2C2Δ hasonló az ABCΔ-höz, s oldalai legyenek az ABCΔ oldalainak λ-szorosai, tehát az A2B2, B2C2, C2A2 oldalak rendre az AC1, BA1, CB1 távolságokkal egyenlők. Ezekre az oldalakra felmérjük a C2A3=CA1, A2B3=AB1, B2C2=BC1 távolságokat, amit 1-λ<λ miatt megtehetünk. Ezzel biztosítottuk, hogy az A2C2A3, B2A2B3, C2B2C3 háromszögek rendre egybevágók a B1CA1, C1AB1, A1BC1 háromszögekkel, s így az A2A3, B2B3, C2C3 távolságok összege az A1B1C1Δ kerületével egyenlő. Minthogy az A3, B3, C3 pontok felvételénél az A2B2C2Δ oldalaira ezeknek az oldalaknak ugyanannyiszorosát, t. i. μ=1-λλ-szorosát mértük fel, teljesülnek előzőleg bizonyított állításunknak feltételei. E szerint tehát az A2A3, B2B3, C2C3 távolságok összege az A2B2C2Δ kerületénél, vagyis az A1B1C1Δ kerülete az ABCΔ kerületének λ-szorosánál kisebb.
 
Megjegyzés: Nem nehéz e második megoldást úgy alakítani, hogy az 12<λ<1 kirovás szükségessége is kiolvasható legyen. Elegendő ugyanis a megoldásban szereplő első egyenlőtlenséghez hozzáfűzni, hogy amennyiben a γ1 és γ2 szögek -180∘ és 180∘ közé esnek, s összegük pozitív, úgy ez az első egyenlőtlenség csak akkor teljesül, ha a γ1 és γ2 szögek mindegyike pozitív. Ebből a megállapításból kiindulva megoldásunk gondolatmenetének változatlan megtartása (s előjeles távolságok és szögek használata) mellett a mondott eredményhez juthatunk, ezt azonban itt nem részletezzük.