Kezdőlap


Cím:	A valószínűség elemei (2. közl.)
Szerző(k):	Prékopa András
Füzet:	1953/április, 97 - 107. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

(2., befejező közlemény)

A feltételes valószínűség

A következő példa egy új és a valószínűség számításban fontos fogalomhoz, a feltételes valószínűsítéséhez fog elvezetni. Tekintsünk egy 40 nőből és 60 férfiból álló csoportot és tegyük fel, hogy a nők közül 3, a férfiak közül pedig 4 színvak. A csoport tagjai szemvizsga előtt állanak és az orvos találomra kiválaszt valakit a 100 vezetéknevet tartalmazó névjegyzékben. Mivel a névjegyzékben csak a vezetéknév van feltüntetve, azért a kiválasztott egyén lehet férfi is, meg nő is, és annak valószínűsége, hogy a kiválasztott egyén ,,színvak nő'' legyen nyilván

\frac{3}{100} = 0, 003

, míg annak a valószínűsége, hogy az így kiválasztott egyén színvak legyen

\frac{7}{100} = 0, 07

. De mihelyt a kiválasztott egyén belép a vizsgálati helységbe és látjuk, hogy nő, akkor a lehetséges esetek száma már csak 40, a feltett kérdésre nézve kedvező esetek száma 3, és így annak valószínűsége, hogy a kiválasztott egyén ‐ feltéve, hogy ez nő ‐ színvak legyen

\frac{3}{40} = 0, 075

. (A színvakság abszolút ‐ vagyis feltétel nélküli ‐ valószínűsége, mint láttuk,

0, 07

.)
Ez utóbbi példában egy színvak ember kiválasztásának a valószínűségét kerestük meg azon feltétel mellett, hogy a vizsgálatra nőt választottunk. Ez a feltétel annak az eseménynek a bekövetkezését jelenti, hogy a találomra kiválasztott egyén nő.
Általában ha egy esemény bekövetkezésének a valószínűségét olyan körülmények között keressük, hagy közben egy másik esemény bekövetkezését feltételezzük, a nyert valószínűséget feltételes valószínűségnek nevezzük. Amikor feltételes valószínűségről beszélünk, mindig meg kell mondanunk, hogy melyik az az esemény, amelynek a bekövetkezését feltételeztük, vagy ahogy mondani szoktuk: amelyre az eredeti eseményünk valószínűségét vonatkoztatjuk.
Előfordul, hogy a feltételes valószínűség kiszámítása bonyolult feladatot állít elénk, ezért le fogunk vezetni egy képletet, amelynek segítségével adott esetben a feladatot lényegesen egyszerűbben tudjuk megoldani. A fent tárgyalt példában a keresett valószínűség

\frac{3}{40}

volt. Jelöljük

A

-val azt az eseményt, hogy színvakot,

B

-vel pedig, hogy nőt választunk a 100 ember közül. Jelöljük továbbá

v_{A B}

-vel annak az eseménynek a valószínűségét, amely abban áll, hogy a kiválasztott egyén egyszerre színvak is és nő is,

v_{B}

-vel pedig annak a valószínűségét, hogy a feltételként szereplő esemény bekövetkezzék, vagyis, hogy a csoportból kiválasztott ember nő. Mivel a csoportban összesen 3 színvak nő van, ezért

v_{A B} = \frac{3}{100}

, a nők pedig együttvéve 40-en vannak, tehát

v_{B} = \frac{40}{100} = \frac{2}{5}

. Ennek alapján

\begin{matrix} v = \frac{3}{40} = \frac{\frac{3}{100}}{\frac{40}{100}} = \frac{v_{A B}}{v_{B}} . \end{matrix}

Most bizonyítsuk be, hogy ez a képlet nem csupán a mi speciális példánk esetében, hanem minden esetben érvényes. Tekintsünk két eseményt és az előzőekhez hasonlóan jelöljük őket

A

-val, illetve

B

-vel. Állapodjunk meg továbbá abban, hogy

k_{A B}

-vel jelöljük a két esemény együttes bekövetkezéséhez, mint újabb eseményhez tartozó kedvező esetek számát,

v_{A B}

-vel a megfelelő valószínűséget,

k_{B}

-vel a

B

esemény kedvező eseteinek a számát és

v_{B}

-vel a megfelelő valószínűséget. Végül a lehetséges esetek számát jelöljük

n

-nel és az

A

eseménynek azon feltétel melletti valószínűségét, hogy a

B

esemény bekövetkezik

v_{A / B}

-vel (olvasd: az

A

eseménynek a

B

eseményre vonatkozó feltételes valószínűsége). Ha az

A

esemény bekövetkezését olyan körülmények között vizsgáljuk, hogy a

B

esemény bekövetkezését feltételezzük, akkor nyilvánvaló, hogy a feltételes valószínűség kifejezésében a lehetséges esetek számának a szerepét

k_{B}

fogja játszani. A kedvező esetek számát pedig az határozza meg, hogy ezen

k_{B}

eset közül mennyi azoknak az eseteknek a száma, amelyek az

A

eseményre nézve is kedvezőek. Mivel jelöléseink szerint ez a szám

k_{A B}

, azért

\begin{matrix} v_{A / B} = \frac{k_{A B}}{k_{B}} = \frac{\frac{k_{A B}}{n}}{\frac{k_{B}}{n}} = \frac{v_{A B}}{v_{B}} . \end{matrix}

Ez az egyenlőség azt mondja ki, hogy egy eseménynek egy másik eseményre vonatkozó feltételes valószínűségét kiszámíthatjuk úgy, hogy a két esemény együttes bekövetkezésének a valószínűségét elosztjuk a feltételként szereplő esemény bekövetkezésének a valószínűségével.
Gyakran előfordul azonban az az eset, hogy

v_{A / B}

feltételes valószínűség kiszámítása aránylag egyszerű, ellenben nehezebb feladat a két esemény együttes bekövetkezésének, a

v_{A B}

valószínűségét kiszámítani. Ebben az esetben az előbb levezetett képletet felhasználhatjuk a

v_{A B}

kiszámítására. Ugyanis, ha

v_{B}

-t átvisszük a másik oldalra, azt kapjuk, hogy

\begin{matrix} v_{A B} = v_{A / B} \cdot v_{B} . \end{matrix}

A bevezetésben szereplő példában láttuk, hogy annak valószínűsége, hogy a kiválasztott egyén színvak is

(A)

, meg nő is

(B)

v_{A B} = \frac{3}{100} = 0, 03

. Mivel

A

és

B

egymástól nem független események, azért hiba volna

v_{A B}

-t, a szorzási tétel alapján kiszámítani, amikor is azt kapnánk, hogy

v_{A B} = v_{A} \cdot v_{B} = \frac{7}{100} \cdot \frac{40}{100} = 0, 028

. Ellenben a fenti képlet

v_{A B} = v_{B} \cdot v_{A / B} = \frac{40}{100} \cdot \frac{3}{40} = \frac{3}{100}

helyes eredményhez vezet.
Ez az utóbbi képlet tehát akkor jelent segítséget, ha az

A

és a

B

események nem függetlenek, vagyis amikor az együttes bekövetkezés valószínűségét nem lehet a szorzási tétel segítségével kiszámítani. Ha a két esemény független, akkor

\begin{matrix} v_{A B} = v_{A} \cdot v_{B} \end{matrix}

és ezért

\begin{matrix} v_{A / B} = \frac{v_{A B}}{v_{B}} = \frac{v_{A} \cdot v_{B}}{v_{B}} = v_{A} . \end{matrix}

Nyilvánvaló továbbá, hogy

v_{A B} = v_{B A}

-val, hiszen

v_{A B}

A

és

B

esemény,

v_{B A}

pedig a

B

és

A

esemény együttes bekövetkezését jelenti, tehát

\begin{matrix} v_{B / A} = \frac{v_{B A}}{v_{A}} = \frac{v_{B} \cdot v_{A}}{v_{A}} = v_{B} . \end{matrix}

Ezek a formulák azt fejezik ki, hogy ha két esemény egymástól független, akkor az egyiknek a másikra vonatkoztatott feltételes valószínűsége egyenlő az illető esemény abszolút valószínűségével.
Még világosabbá válik a feltételes valószínűség fogalma, ha például a bevezetésben szereplő példával kapcsolatban feltesszük a következő kérdést: Egy találomra kiválasztott egyén színvaknak bizonyul; mekkora annak a valószínűsége, hogy e kiválasztott színvak egyén nő?
Képletünk szerint a keresett feltételes valószínűség

\begin{matrix} v_{A / B} = \frac{v_{A B}}{v_{B}} \end{matrix}

ahol

v_{A B}

az együttes bekövetkezés (színvak is. meg nő is) valószínűsége, vagyis

v_{A B} = \frac{3}{100}

, és

v_{B}

a feltételezett esemény bekövetkezésének valószínűsége. Jelen esetben a színvakságot tételeztük fel, tehát

v_{B} = \frac{7}{100}

, és így a keresett feltételes valószínűség

\begin{matrix} v_{A / B} = \frac{v_{A B}}{v_{B}} = \frac{\frac{3}{100}}{\frac{7}{100}} = \frac{3}{7} \approx 0, 429. \end{matrix}

Ezzel szemben az abszolút valószínűsége annak, hogy egy kiválasztott egyén nő

v_{A} = \frac{40}{100} = 0, 4

.
A most következő példák közül csupán a harmadikban és a negyedikben fogjuk a képleteinket alkalmazni, az előbbiben a

v_{A / B}

az utóbbiban pedig a

v_{A B}

kiszámítására.
Példák. 1. Egy urnában van 10 piros, 5 fehér és 2 zöld golyó. Húzzunk ki egymás után visszatevés nélkül két golyót az urnából. Tegyük fel, hogy az elsőre kihúzott golyó piros (

B

esemény), mekkora ebben az esetben annak a valószínűsége, hogy a másodikra kihúzott golyó is piros színű?
Ha az első golyó piros színű, akkor az urnában már csak 9 piros golyó marad, tehát akkor annak a valószínűsége, hogy másodszor is pirosat húzunk:

v_{A / B} = \frac{9}{16}

2. Tekintsük valamely városban a kétgyermekes családokat. Jelöljük röviden a fiúkat

f

, a lányokat pedig

l

betűvel, akkor egy kétgyermekes család két betűvel jellemezhető. Ha az első betűvel az idősebb gyerekeket jelöljük, akkor a következő típusú családok lehetségesek:

f f

f l

l f

l l

. Tegyük fel, hogy mindegyik típusú családból ugyanannyi él a városban. Ha kiválasztunk egy olyan családot, ahol tudjuk, hegy egy fiú van (

B

esemény), mekkora annak a valószínűsége, hogy mindkét gyermek fiú? (

A

esemény).
Mivel azok a családok, amelyeknél legalább egy fiú van, háromszor annyian vannak, mint azok, amelyeknél két fiú van, tehát a keresett valószínűség:

v_{A / B} = \frac{1}{3}

3. Egy könyvesbolt 40 db. könyvet szállít egy üzemi könyvtár számára. A könyvek között van 4 db József Attila verseskötet. A 40 könyvet négy 10-es csomagba csomagolják. Tegyük fel, hogy a csomagolás rendszertelenül történik, vagyis minden csomagolási lehetőség egyformán valószínű. Ha a könyvtárban a könyvek megérkezése után egy József Attila kötetet akarnak elővenni, mekkora annak a valószínűsége, hogy ha az első csomagban egy kötetet sem találtak (

B

esemény), a másodikban legalább egy kötet lesz?
Számítsuk ki előbb annak a valószínűségét, hogy a másodikban sem találnak egy kötetet sem. (

A

esemény). Annak a valószínűsége, hogy az első kibontott csomagban egy kötet se legyen

\begin{matrix} v_{B} = (\binom{36}{10}) / (\binom{40}{10}) = \frac{36!}{10! 26!} / \frac{40!}{10! 30!} = \frac{36! 30!}{26! 40!} \end{matrix}

mert 40 könyvből 10-et

(\binom{40}{10})

-féleképpen lehet kiválasztani, míg abból a 36 könyvből, amelyek között nincs József Attila kötet, 10 könyvet

(\binom{36}{10})

-féleképpen választhatunk. Az előbbi a lehetséges, az utóbbi pedig a kedvező esetek számát adja meg. Annak a valószínűsége, hogy sem az elsőben, sem a másodikban ne legyen József Attila kötet:

\begin{matrix} v_{A B} = (\binom{36}{10}) (\binom{26}{10}) / (\binom{40}{10}) (\binom{30}{10}) = \frac{36!}{10! 26!} \cdot \frac{26!}{10! 16!} / \frac{40!}{10! 30!} \cdot \frac{30!}{10! 20!} = \frac{36! 20!}{40! 16!} . \end{matrix}

Tehát annak a valószínűség, hogy ha az első csomagban nincs egy kötet sem, akkor a másodikban sincs:

\begin{matrix} v_{A / B} = \frac{v_{A B}}{v_{B}} = \frac{36! 20!}{40! 16!} / \frac{36! 30!}{26! 40!} = \frac{20! 26!}{16! 30!} = \frac{17 \cdot 18 \cdot 19 \cdot 20}{27 \cdot 28 \cdot 29 \cdot 30} = \frac{17 \cdot 19}{3 \cdot 7 \cdot 29 \cdot 3} = \frac{323}{1827} \approx 0, 177 \end{matrix}

és így a keresett valószínűség:

\begin{matrix} v = 1 - v_{A / B} \approx 0, 823 \end{matrix}

4. Egy urnában van 5 fehér és 6 fekete golyó. Visszatevés nélkül kihúzunk egymás után kettőt. Mennyi annak a valószínűsége, hogy két fehéret húzunk?
Jelenleg két nem független esemény együttes bekövetkezésének a valószínűségét keressük. Annak a valószínűsége, hogy az első golyó fehér

v_{B} = \frac{5}{11}

. Az a feltételes valószínűség pedig, hogy ha az első golyó fehér (

B

esemény), a második is fehér (

A

az az esemény, hogy a második golyó fehér):

v_{A / B} = \frac{4}{10} = \frac{2}{5}

. Tehát az együttes bekövetkezés valószínűsége:

\begin{matrix} v_{A B} = v_{b} \cdot v_{A / B} = \frac{5}{11} \cdot \frac{2}{5} = \frac{2}{11} . \end{matrix}

A geometriai valószínűség

Az eddigiekben kizárólag olyan kísérletek köré csoportosuló események valószínűségeit számoltuk ki, melyek ‐ mint pl. a kockadobás ‐ csupán véges számú különböző eredményre vezethetnek. Ebben a fejezetben pedig a végtelen sok lehetséges eredménnyel rendelkező kísérletekkel és a kísérletek elvégzése után bekövetkezett események valószínűségeinek a kiszámításával fogunk foglalkozni. A ,,geometriai valószínűség'' elnevezést az a tény indokolja, hogy azok a feladatok, amelyek a geometriai valószínűség példái gyanánt szolgálnak, mind geometriailag szemléltethetők, és a valószínűség kiszámítása pedig egyszerű szakaszok mérése, terület-, illetve köbtartalom számításra vezethető vissza.
Lássunk egy példát. Valaki egy köralakú céltáblára vaktában lead egy lövést, de úgy, hogy a céltáblát azért biztosan eltalálja. A céltábla 10 koncentrikus körből áll, amelyek 9 körgyűrűt alkotnak, amelyeknek szélessége egyenlő a legkisebb (10-es) kör sugarával. Kérdés, hogy mekkora valószínűséggel talál az illető a 10-es körbe? Mivel a lövés vaktában történt, semmi jogunk sem lenne azt mondani, hogy a golyó nagyobb valószínűséggel csapódik be a céltábla bal felső negyedébe, mint pl. a jobb alsóba. Ezért egyenlő területű részeknek egyenlő valószínűséget kell tulajdonítanunk. A valószínűség definíciója hasonló lesz ahhoz a definícióhoz, amelyet az 1. közlemény elején a véges esetre vonatkozólag vezettünk be. Ez a definíció a következő. Ha

v

-vel jelöljük annak a valószínűségét, hogy a lövedék egy

t

területű idom valamelyik pontjába csapódjék be és

T

pedig az egész céltábla területét jelenti, akkor

\begin{matrix} v = \frac{t}{T} = \frac{kedvező terület}{lehetséges terület} . \end{matrix}

Ennek alapján annak a valószínűsége, hogy a lövedék a céltábla bal felső negyedébe csapódjék be:

\begin{matrix} v = \frac{\frac{T}{4}}{T} = \frac{1}{4} . \end{matrix}

Számítsuk ki ezek után annak a valószínűségét, hogy a lövés a 10-es körbe találjon. Jelöljük

R

-rel az egész céltábla sugarát, akkor a 10-es kör sugara

R / 10

.Az előbbi definíció szerint

\begin{matrix} v = \frac{t}{T} = \frac{\frac{R^{2}}{100} π}{R^{2} π} = \frac{1}{100} \end{matrix}

Amint az 1. közlemény elején tettük, most is élnünk kell egy feltevéssel. Amikor véges számú elemi eseménnyel dolgoztunk, azt mondtuk, hogy csak azokkal a kísérletekkel foglalkozunk, amelyekhez tartozó elemi események egyenlő eséllyel következnek be, tehát egyik sincs a bekövetkezés szempontjából előnyösebb helyzetben, a többivel szemben. Ezt a feltevést most a végtelen sok elemi esemény esetében módosítani fogjuk. A céltábla példájának esetében az elemi eseményeket a céltábla összes pontjai jelentik. Most nem az elemi eseményekre vonatkozólag teszünk kikötést, hanem az elemi események összességére vonatkozólag; ez a következő: feltesszük, hogy az egyenlő területű idomok nincsenek egymással szemben előnyösebb, vagy hátrányosabb helyzetben, hanem a kísérlet eredményét jelentő elemi esemény egyenlő eséllyel helyezkedik el két egyenlő területű idom akármelyikének a belsejében.
Természetesen nemcsak síkbeli feladatok tartoznak a geometriai valószínűség kiszámításának feladatai közé; vannak olyan problémák, amelyek egy egyenesen és olyanok, amelyek a térben szemléltethetők. Az előbbi feltevésünket mindenesetre ezekben az esetekben is fenntartjuk, csupán a ,,terület'' szót kell a ,,hosszúság'' illetve a ,,köbtartalom'' szavakkal felcserélnünk. A valószínűség definíciójában hasonlóképpen csak a szavakat kell felcserélnünk, tehát egy egyenesmenti probléma esetében a valószínűség a kedvező és a lehetséges hosszúság, egy térbeli probléma esetében pedig a kedvező és lehetséges köbtartalom hányadosával egyenlő.
Mielőtt rátérnénk a példák tárgyalására, megjegyezzük, hogy a geometriai valószínűség érdekesebb és komolyabb nehézséget jelentő feladatai nem azok, amelyeknél a geometriai modellt készen kapjuk és csak a területszámítást kell elvégeznünk, hanem inkább azok, amelyekre előbb a modellt is fel kell állítanunk, tehát amelyeknél előbb azt kell tisztáznunk, hogy melyek azok a területek, amelyeket össze kell hasonlítanunk.

Példák. 1. Két ember

A

és

B

megbeszéli, hogy 12 és 1 óra között egy meghatározott helyen találkoznak. Mind a ketten elfoglalt emberek, ezért megállapodnak abban, hogy az, aki elsőnek érkezik a megbeszélt helyre, 20 percet vár és azután elmegy. Kérdés, mekkora a valószínűsége annak, hogy a találkozás sikerül?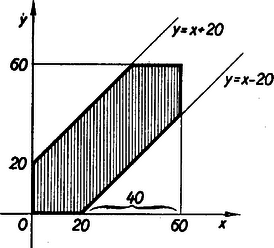

1. ábra

Rajzoljunk egy koordináta rendszert és a vízszintes tengelyen a 0 és 60 közé mérjük fel

A

, a függőleges tengelyen pedig hasonlóképen a 0 és 60 közé mérjük fel

B

érkezésének időpontját, ha a perceket 12 órától kezdődően számítjuk. Ilyenformán

x

jelenti

A

y

pedig

B

megérkezésének időpontját. A két ember a találkozást akkor nem mulasztja el, ha

x

nem nagyobb, mint

y + 20

és

y

sem nagyobb, mint

x + 20

. Tehát

\begin{matrix} x ≦ y + 20, vagyis y≧x-20, y≦x+20. \end{matrix}

Azok a pontok, amelyeknek koordinátái pozitívak, ezt a két egyenlőtlenséget kielégítik és amellett

x ≦ 60

és

y ≦ 60

az 1. ábrán a sraffozott sávot jelentik. Ennek a területe a kedvező, a 60 oldal hosszúságú négyzet területe pedig a lehetséges terület. Tehát a találkozás valószínűsége:

\begin{matrix} v = \frac{t}{T} = \frac{60^{2} - 40^{2}}{60^{2}} = {1 - (\frac{2}{3})}^{2} = \frac{5}{9} . \end{matrix}

2. Egy egységnyi hosszúságú szakaszt két találomra kiválasztott pont segítségével három részre osztunk. Mennyi annak a valószínűsége, hogy a három szakaszból háromszög szerkeszthető? A problémát megint egyszerű területszámítási feladatra vezetjük vissza. Jelöljük az egységnyi hosszúságú szakasz kezdő és végpontját 0-val illetve 1-gyel és a rajta kiválasztott két pontot

x

-szel és

y

-nal. (2. ábra).

2. ábra

Milyen kapcsolatnak kell lennie az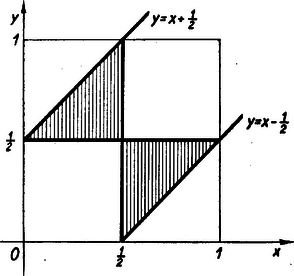

x

és

y

között ahhoz, hogy az osztópontok közötti távolságokból egy háromszöget össze tudjunk állítani? A háromszög jellemző tulajdonsága az, hogy bármelyik két oldalának az összege nagyobb a harmadik oldalnál. Ha az

x

pont az

y

ponttól balra fekszik, akkor egy háromszög megszerkeszthető abban az esetben, ha az

x

és

y

eleget tesznek három egyenlőtlenségnek, melyeket azáltal kapunk, hogy veszünk az

x

y - x

és

1 - y

szakaszok közül kettőt, összeadjuk a hosszúságukat és ezt az összeget nagyobbá tesszük a harmadik szakasz hosszánál. Ezek az egyenlőtlenségek a következők:

\begin{matrix} x + (y - x) = y > 1 - y, x + (1 - y) > y - x, (y - x) + (1 - y) = 1 - x > x \end{matrix}

vagy az összevonást elvégezve:

\begin{matrix} y > \frac{1}{2}, x + \frac{1}{2} > y, \frac{1}{2} > x . \end{matrix}

Ha pedig az

y

fekszik az

x

-től balra, akkor ugyanezek az egyenlőtlenségek szükségesek a háromszög szerkesztéshez, csupán az

x

-et és az

y

-t kell egymással, felcserélni:

\begin{matrix} x > \frac{1}{2}, y + \frac{1}{2} > x, \frac{1}{2} > y . \end{matrix}

3. ábra

Ha most az

x

y

értékpárt, tehát az 1 hosszúságú szakasz egy felosztását a koordináta sík egységnyi oldalhosszúságú négyzetének pontjaként ábrázoljuk (3. ábra), akkor az első egyenlőtlenség sorozat ‐ figyelembe véve még, hogy itt

x < y

volt ‐ annyit jelent, hogy az

x

y

koordinátájú pont az ábrán a baloldalt és feljebb elhelyezkedő sraffozott háromszög belsejében fekszik. Hasonlóképpen a második egyenlőtlenség sorozat ‐ az

y < x

kiegészítéssel ‐ a másik vonalkázott háromszöget szolgáltatja. Ennek alapján egy háromszög megszerkeszthetőségének a valószínűsége:

\begin{matrix} v = \frac{t}{T} = \frac{2}{8} = \frac{1}{4} \end{matrix}

Az összeadási, a szorzási tétel és a feltételes valószínűség

A geometriai valószínűség esetében nagyon jól lehet ezt a két tételt és az utóbbi fogalmat szemléltetni. Tételeink bizonyítása most kézenfekvő. Az összeadási tétel egyszerűen azon alapszik, hogy egymást kizáró események esetében az egész kedvező terület

t

, nem más, mint az egyes események

t_{1}

és

t_{2}

kedvező területeinek az összege, hiszen az ezen területekhez tartozó geometriai idomok az egymást kizárás követelménye miatt nem nyúlhatnak egymásba. Tehát

\begin{matrix} v = \frac{t}{T} = \frac{t_{1} + t_{2}}{T} = \frac{t_{1}}{T} + \frac{t_{2}}{T} = v_{1} + v_{2} \end{matrix}

A szorzási tételt vizsgáljuk meg a következő esetben. Egy az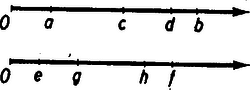

x

tengelyen

a

-tól

b

-ig terjedő szakaszból válasszunk találomra egy pontot és kérdezzük, mi annak a valószínűsége, hogy az

a

b

szakasznak a

c

és

d

pontok által meghatározott részintervallumában fekvő pontot választunk. Ha ennek a valószínűségét

v_{A}

-val jelöljük, akkor

v_{A} = \frac{d - c}{b - a}

(4. ábra).

4. ábra

Annak a valószínűsége, hogy egy másik választásnál a kapott pont egy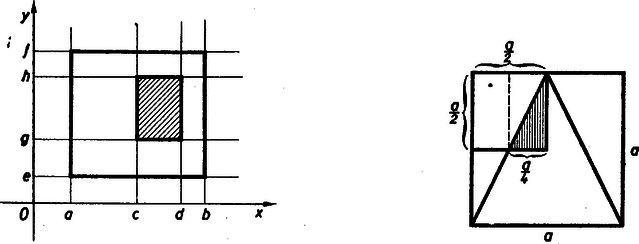

e

f

intervallum

g

h

, részintervallumába essék:

v_{B} = \frac{h - g}{f - e}

(4. ábra). Tegyük fel, hogy a két pontnak a kiválasztása egymástól függetlenül történik és keressük meg a fenti 2 esemény együttes bekövetkezésének

v_{A B}

valószínűségét. Vegyünk fel egy koordináta‐rendszert és a két pont helyzetét ábrázoljuk egyetlen síkbeli pont segítségével oly módon, hogy annak

x

koordinátája az első,

y

koordinátája pedig a második pont helyzetét mutassa az

x

illetve az

y

tengelyen. Az 5. ábrából leolvasható, hogy a kedvező terület

t = (c - d) \cdot (h - g)

, a lehetséges terület pedig

T = (b - a) (f - e)

, tehát akkor az együttes bekövetkezés valószínűsége:

\begin{matrix} v_{A B} = \frac{(c - d) (h - g)}{(b - a) (f - e)} = \frac{c - d}{b - a} \cdot \frac{h - g}{f - e} = v_{A} \cdot v_{B} . \end{matrix}

Más esetben, amikor nem az egyenesen választjuk ki találomra a pontjainkat, hanem a síkban, vagy a térben, a szorzási tétel már nem tárgyalható szemléletesen, mert háromnál magasabb dimenziójú terekben kellene dolgoznunk, ahol geometriai szemléletünk csődöt mond.

5. ábra 6. ábra

Jól megérthetjük a feltételes valószínűség fogalmát, ha megvizsgálunk egy erre vonatkozó példát a geometriai valószínűség esetében. Egy

a

oldalhosszúságú, négyzetalakú céltáblára találomra leadunk egy lövést úgy, hogy a céltáblát azért biztosan eltaláljuk. Tegyük fel, hogy a puska balra és felfelé hord, tehát a lövés a bal felső négyzetbe fog esni és kérdezzük, hogy mekkora annak a valószínűsége, hogy ezen feltétel mellett a lövés a céltábla alapjára elhelyezett,

a

magasságú egyenlő szárú háromszög belsejébe essék? A 6. ábráról leolvasható, hogy ez a valószínűség

\frac{1}{4}

. A geometriai valószínűség esetében nem kell külön bizonyítanunk, hogy a feltételes valószínűség úgy számítható ki, hogy a két esemény együttes bekövetkezésének a valószínűségét elosztjuk a feltételt jelentő esemény valószínűségével, mert ebben az esetben ez nyilvánvaló.

A valószínűségszámítás újabb útjai

Egyszerűség kedvéért szorítkozzunk arra az esetre, amikor véges számú elemi eseményről van szó. Mi eddig csak olyan kísérleteket tekintettünk, amelyeknek az eredményei egyenlő valószínűséggel következhetnek be, tehát egyik sincs előnyben a többivel szemben. A gyakorlat azonban tömegével szolgáltatja azokat a példákat, amelyeknél ez a feltétel nem teljesül. Nem mondhatjuk azt, hogy ha az ég teljesen felhőtlen, akkor is

\frac{1}{2}

annak a valószínűsége, hogy 5 percen belül essék az eső, mert csak két lehetőség van: vagy esik, vagy nem esik. Hasonlóképen nem

\frac{1}{3}

annak a valószínűsége, hogy egy erősebb labdarúgó csapat legyőzzön egy nála sokkal gyengébb csapatot, ugyanis jóllehet három lehetséges eset van, mégis egy jóval erősebb csapat

\frac{1}{3}

-nál nagyobb valószínűséggel győz. Úgyszintén nem

\frac{1}{3}

annak a valószínűsége, hogy egy nagykörúti villamos megállónál az első beérkező villamos 66-os lesz, mert a 66-os ritkábban jár, mint a 6-os és a 4-es; még sok más példát lehetne erre vonatkozólag felhozni. A valószínűségnek tehát az a definíciója, amely szerint a valószínűség a kedvező esetek és lehetséges esetek számának a hányadosa nem minden esetben alkalmas a természet leírására, a valóság helyes megismerése. A modern felfogás szerint a valószínűség mindenféle tőlünk származó megkonstruálása helytelen és elvetendő, mert a valószínűség nem tőlünk függő fogalom, amely aszerint változik, hogy ki‐ki mit gondol róla, hanem tőlünk függetlenül létező, objektív valóság, amelyet a természet szolgáltat. Egy esemény valószínűsége tehát egy adott szám, az eseménynek egy fizikai állandója éppen úgy, mint ahogy egy testnek fizikai állandója a saját tömege. Az azután megint más kérdés, hogy hogyan állapítjuk meg ezt a számot: az esemény valószínűségét. Ezzel a statisztika foglalkozik, amelynek megvannak erre vonatkozólag a jól kidolgozott módszerei. A valószínűségszámításnak az a feladata, hogy megadott valószínűségekből újabb valószínűségeket számítson ki Ahhoz azonban, hogy a valószínűségekkel számolni tudjunk, tisztáznunk kell a valószínűség jellemző tulajdonságait, fel kell állítanunk az axiómákat, amelyeknek nyilvánvalóan eleget tesz. Ezeket az axiómákat 1933-han Kolmogorov szovjet matematikus adta meg és az azóta eltelt 20 év bebizonyította, hogy egyedül Kolmogorov elmélete az, amely a valószínűség számítást kielégítő módon megalapozza. Kolmogorov axiómái a következők:

1. Tekintsük az egy kísérlet köré csoportosuló eseményeket tehát az elemi eseményeket és az ezek által képezhető összetett eseményeket; minden eseménynek van egy

v

valószínűsége, amely 0 és 1 között van:

\begin{matrix} 0 ≦ v ≦ 1 \end{matrix}

2. Ha két esemény (

A

és

B

) kizárja egymást és az egyiknek

v_{A}

másiknak pedig

v_{B}

a valószínűsége, akkor annak a valószínűsége, hogy vagy az egyik, vagy a másik bekövetkezzék:

\begin{matrix} v = v_{A} + v_{B} . \end{matrix}

Amint látjuk az összeadási tétel most axióma lett. Hasonlóképpen elveszti tétel jellegét a szorzási tétel is. Jelen esetben ez nem más, mint a függetlenség definíciója. Két eseményt függetlennek nevezünk, ha együttes bekövetkezésük valószínűsége egyenlő a két esemény valószínűségének a szorzatával:

\begin{matrix} v_{A B} = v_{A} \cdot v_{B} . \end{matrix}

A feltételes valószínűség kiszámításának a képlete szintén definíció. Az

A

eseménynek a

B

eseményre vonatkozó feltételes valószínűsége alatt a

\begin{matrix} v_{A / B} = \frac{v_{A B}}{v_{B}} . \end{matrix}

hányadost értjük, ahol

v_{A B}

az együttes bekövetkezés,

v_{B}

pedig a feltételként szereplő esemény bekövetkezésének a valószínűsége. Ha az események függetlenek, akkor

\begin{matrix} v_{A / B} = \frac{v_{A B}}{v_{B}} = \frac{v_{A} \cdot v_{B}}{v_{B}} = v_{A}, \end{matrix}

vagyis, ebben az esetben a feltételes valószínűség megegyezik az abszolút valószínűséggel.
Kolmogorov elmélete speciális esetként tartalmazza a klasszikus valószínűségszámítást. Ugyanis, ha a valószínűség speciálisan a

\frac{k}{n}

hányados által van értelmezve, akkor az első axióma nyilvánvalóan, a második pedig az 1. közleményben tárgyalt összeadási tétel értelmében teljesül. Hogy mely esetekben van a valószínűség a

\frac{k}{n}

hányados által adva, azt a nagy számok törvénye alapján ellenőrizhetjük. Hasonlóképpen, a nem egyenlő valószínűségű elemi események esetében is, a valószínűség megállapításának egyik leggyakoribb és legegyszerűbb módszere a nagy számok törvényén alapszik. Igen nagy számú kísérletet elvégeztünk, megállapítjuk, hogy ezek közül hányszor következett be az az esemény, amelynek a valószínűségét keressük és ezt a számot elosztjuk a kísérletek számával. Ebből máris világos, hogy a valószínűség tényleg 0 és 1 között van. A második axióma is nyilvánvalóvá válik (az axiómák nyilvánvaló állításokat foglalnak magukban) ha meggondoljuk, hogy ha két esemény kizárja egymást, és 100 kísérletet végeztünk, miközben az eseményeink 10-szer illetve 15-ször következtek be, akkor az az eredmény, hogy vagy az egyik, vagy a másik bekövetkezik, 25 esetben következett be.