Cím: 1951. évi Kürschák József matematikai tanulóverseny
Füzet: 1952/február, 2 - 11. oldal  PDF  |  MathML 
Témakör(ök): Kürschák József (korábban Eötvös Loránd)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A Bolyai János Matematikai Társulat 1951. október 27-én egyidejűleg rendezte Budapesten, Szegeden, Debrecenben, Miskolcon, Veszprémben, Pécsett és Egerben az ez évi Kürschák József matematikai tanulóversenyt. A versenyben az 1951-ben érettségizettek és középiskolás diákok vehettek részt. A résztvevők és beadott dolgozatok száma: Budapesten 170 részvevő 108 dolgozattal, Szegeden 43 résztvevő 16 dolgozattal, Debrecenben 33 résztvevő 15 dolgozattal, Miskolcon 29 részvevő 14 dolgozattal, Veszprémben 40 részvevő 20 dolgozattal, Pécsett 55 részvevő 19 dolgozattal, Egerben 24 részvevő 7 dolgozattal, összesen 394 részvevő 199 dolgozattal. A verseny feladatai a következők voltak:

 

1. Az a oldalú ABCD négyzet BC oldalára felmérjük a BE=a3 távolságot, DC oldalának meghosszabbítására pedig a CF=a2 távolságot. Bizonyítandó, hogy az AE és BF egyenesek metszéspontja a négyzet köré írt körön van.
2. Mely 1-nél nagyobb m egész számokra igaz az, hogy m osztója az 1, 2, 3, ..., m-1 számok szorzatának?
3. Négy félsík úgy helyezkedik el egy síkban, hogy együttesen az egész síkot lefedik, azaz a síknak mindegyik pontja legalább az egyik félsíknak belső pontja. Bizonyítandó, hogy a négy félsík közül kiválasztható három úgy, hogy e három félsík is lefedi együttesen az egész síkot.
 

A Bolyai János Matematikai Társulat elnöksége által kiküldött versenybizottság, melynek tagjai Gallai Tibor, Kárteszi Ferenc, Surányi János, Vincze István és Hajós György előadó, 1951. november 8-án tartott ülésén a következő jelentést fogadta el:
,,A versenyre szép számmal jelentkeztek a versenyzők s a beadott dolgozatok száma lényegesen nagyobb volt mint a korábbi évek versenyein. Legtöbben az első feladatot oldották meg, s legnehezebbnek a harmadik feladat bizonyult.
A beadott dolgozatok közül kiemelkedik Szekerka Pál dolgozata, aki Neukomm Gyula tanár tanítványa s az elmúlt tanévben a budapesti VI. kerületi Rudas László gimnáziumban a III. osztályt végezte el. Az első feladatra valamennyi versenyző közül egyedül ő adott be tisztán elemi geometriai megoldást. A második feladatra adott megoldása kifogástalan s megfogalmazása tömör. A harmadik feladatra is tömören megfogalmazott ügyes megoldást adott be, azonban a dolgozatból nem állapítható meg, vajon szerzője okoskodásának minden részletét meggondolta-e. A bizottság az 1951. évi első Kürschák József-Díjat Szekerka Pálnak ítéli s munkáját 600 forinttal jutalmazza.
Második helyen Kálmán Lajos dolgozatát kell kiemelni, aki Somosi Ferenc tanár tanítványa s az elmúlt tanévben a budapesti V. kerületi Berzsenyi Dániel gimnáziumban a III. osztályt végezte. Az első feladatot analitikusan oldotta meg, a második feladatra helyesen felelt, de feleletének bizonyítása hiányos. Kiemelkedik viszont a harmadik feladatra adott megoldása, mely komoly matematikai gondolkozó készségről és leleményről tanúskodik, bár okoskodásának nem minden apró részletét dolgozta ki. A bizottság az 1951. évi második Kürschák József-Díjat Kálmán Lajosnak ítéli és munkáját 400 forinttal jutalmazza.
Megemlítendő még Fáy Árpád és Seregély József dolgozata. Mindketten 1951-ben érettségiztek. Érdemük különösen a második feladatra adott szép megoldásuk. Fáy Árpád az első feladatra adott, szögfüggvényekkel dolgozó megoldása mellett a harmadik feladattal is eredményesen foglalkozott, bár a lehetséges esetek taglalása hiányos. Seregély József viszont, jóllehet a harmadik feladatnál csak egyfajta lehetséges esettel foglalkozott, az első feladatot szögfüggvények és koordináták használata nélkül oldotta meg. A bizottság Fáy Árpád és Seregély József dolgozatát dicséretben részesíti.''
Az alábbiakban közöljük a megoldásokat Hajós György előadónak a Bolyai János Matematikai Társulat 1951. nov. 17-én megtartott eredményhirdető és díjkiosztó ülésén elhangzott beszámolója alapján.
 

1. feladat.
I. megoldás: Helyezzük a négyzet A csúcspontját derékszögű koordinátarendszer kezdőpontjába, az AB oldalt a pozitív Y tengelyre az AD oldalt a pozitív X tengelyre és tekintsük a négyzetoldalt egységnek (tehát a=1), akkor feladatunk szerint az AE egyenes egyenlete y=3x és a BF egyenes egyenle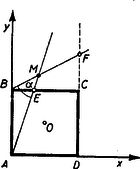te y=1+x2 (1. ábra).
 
 
1. ábra
 

E két egyenes M metszéspontjának koordinátái:
x=0,4ésy=1,2

Számítsuk ki ezen M pont távolságának négyzetét a négyzet O(0,5, 0,5) középpontjától
OM2=(0,5-0,4)2+(0,5-1,2)2=0,12+0,72=0,01+0,49=0,5=0,52+0,52=OA2.


Tehát OM=OA. Ezzel tételünket bebizonyítottuk.
 

II. megoldás: Mivel a kerületi szögek tétele alapján a négyzet köré írt kör bármely pontjától a négyzet oldala 45∘ (illetve az egyik 135∘) alatt látszik, azért tételünk bizonyítást nyert, ha kimutatjuk, hogy AMB∢=α=45∘ (1. ábra). A szögszárak iránytangensei az előbbiek szerint 3 és 12, tehát
tgα=3-121+3⋅12=1,vagyis ténylegα=45∘.
 

III. megoldás: Jelöljük az M pont távolságát a CD négyzetoldaltól MP=a-val, és a BC négyzetoldaltól mért távolságát MQ=b-vel. Az AE egyenes messe a CD négyzetoldal meghosszabbítását G-ben (2. ábr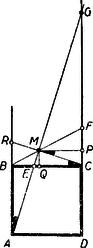a).
 
 
2. ábra
 

Nyilvánvaló, hogy DG=3 és mivel DF a feladat értelmében 1,5, ezért FG=1,5.
Az MABΔ∼MGFΔ és az oldalak aránya
AB:GF=1:1,5=AM:MG.

Ebből következik, hogy AG:MG=2,5:1,5=AD:MP=1:a, vagyis
a=1,52,5=0,6.

Hasonlóképpen BFCΔ∼BMQΔ és így
MQ:FC=BM:BF=AM:AG=1:2,5.

Ebből MQ=b=FC2,5=0,52,5=0,2.
A befogók aránya az, MPC derékszögű háromszögben (0,60,2) ugyanaz, mint az ABE derékszögű háromszögben, miből következik, hogy PMC∢=BAE∢. Mivel pedig PM⊥AB, azért a másik szögszár MC is ⊥AE, vagyis MC⊥MA, ami azt jelenti, hogy az M pont rajta van az AC négyzetátló fölé, mint átmérő fölé rajzolt Thales-körön, amely Thales-kör egyszersmind a négyzet köré írt kör. (Az MC merőlegességére lehetett volna ba=-0,20,6=-13 iránytangensből is következtetni, de nem akartunk ebbe a megoldásba, sem trigonometriát, sem koordináta geometriát közvetlenül bevonni.)
 

IV. megoldás: Messe az AE egyenes a CD oldal meghosszabbítását ismét G-ben és a CM egyenes az AB oldal meghosszabbítását R-ben (2. ábra), akkor az előbbiek alapján
BR:BA=FC:FG=0,5:1,5=1:3,
amiből BR=AB3=BC3. Ebből következik, hogy ABEΔ∼CBRΔ, vagyis MAB∢=MCB∢. De ha két kerületi szög egyenlő és egy-egy száruknak metszéspontja (B) a körön van, akkor a másik két szár metszéspontja (M) is e körön van. (Ez az I. díjnyertes, Szekerka Pál bizonyítása.)
 

V. megoldás: Helyezzük egész ábránkat egy négyzetrácsra úgy, hogy ABCD négyzetünk csúcspontjai egy legkisebb rácsnégyzet csúcspontjaival essenek egybe.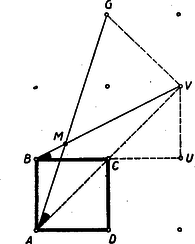
 
 
3. ábra
 

A BC oldalt meghosszabbítva az U rácspontig, az AC átlót pedig a V rácspontig (3. ábra), a keletkezett BUV derékszögű háromszög hasonló az AVG derékszögű háromszöghöz, mert mindkettőben a befogók aránya 2 : 1. Ebből következik, hogy az utóbbi háromszög A-nál fekvő szöge egyenlő az előbbi B-nél fekvő szögével, amiből viszont a kerületi szögek tétele alapján (hasonlóképpen mint a IV. megoldásban) következik, hogy M rajta van a négyzet köré írt körön.
 

VI. megoldás: Húzzuk meg az AU egyenest (4. ábra), ez nyilván párhuzamos a BM egyenessel, mert mindkettő iránytangense 12. Az AUG háromszög nyilván derékszögű egyenlő szárú és így 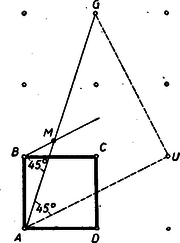A∢-e 45∘-os.
 
 
4. ábra
 

Ennek váltószöge, az AMB∢ tehát szintén 45∘-os, amivel tételünket bebizonyítottuk. (L. a II. megoldást.)
 

2. feladat.
Megoldás: Mindenekelőtt nyilvánvaló, hogy ha m=p prímszám, akkor nem lehet osztója az 1. 2. 3. ...(p-1) szorzatnak. Tehát csak az összetett számok jönnek tekintetbe.
Ha m felbontható két különböző egész szám szorzatára, vagyis m=ab, ahol a≠b, akkor m osztója a fenti szorzatnak, mert hiszen az 1. 2. 3. ...(m-1) szorzatban feltétlenül előfordul mind az ,,a'', mind a ,,b'' mint tényező.
Hátramarad még az az eset, mikor az m csak két egyenlő tényező szorzatára bontható fel, vagyis midőn m=p2 egy prímszám négyzete, akkor az 1. 2. 3. ...(p2-1) szorzat csak akkor osztható p2-tel, ha a tényezősorban p és 2p előfordul, vagyis ha 2p<p2, azaz p>2. Ezt az egyenlőtlenséget p=2 kivételével minden prímszám kielégíti.
Kimodhajtuk tehát, hogy m bármilyen összetett szám lehet a 4 kivételével, és más szám nem felel meg.
 

Megjegyzések: 1. Feladatunk megoldása változatlan marad, ha csak az 1. 2. 3. ...(m-2) szorzatra szorítkozunk, mert hiszen (m-1) és m-nek nem lehet közös osztója.
2. Csak nagyon kevéssé módosul a megoldás, ha az 1. 2. ...[m2] szorzatra szorítkozunk, ahol a szögletes zárójel jelenti az m2 számban foglalt legnagyobb egész számot. A prímszámok természetesen megint ki vannak zárva, viszont az m=ab (a≠b) alakú összetett számok ismét eleget tesznek a követelményeknek, mert 2≤a és 2≤b miatt
b=ma≤m2ésa=mb≤m2.

Hátra van még az m=p2 eset, hol az oszthatósághoz most szükséges, hogy 2p≤p22, vagyis p≥4. Tehát a p=2-n kívül a p=3 is ki van zárva. Ez esetben tehát a 4 és 9 kivételével az összes összetett számok, és csakis ezek, tesznek eleget a követelménynek.
Ez a feladat Kürschák Józseftől ered és még ő sorolta be a kitűzendő versenyfeladatok közé.
 

3. feladat.
I. megoldás: Két félsík elhelyezése után az 5. ábrában feltüntetett 4 helyzet állhat elő, ahol a határegyenes sraffozott oldala jelenti a félsíkot.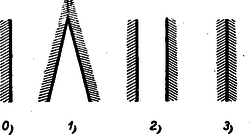
 
 
5. ábra
 

A (0) helyzetben a két határegyenes párhuzamos és az egyik félsík a másik félsíkot teljesen elfedi, tehát ez utóbbi máris felesleges. Ezzel a helyzettel már nem kell foglalkoznunk.
Tehát csak az (1), (2) és (3) eseteket kell a továbbiakban figyelembe venni, mikor egy ék, egy síksáv, illetőleg egy egyenes (a két félsík közös határegyenese) marad fedetlenül.
A harmadik félsík hozzáillesztésével (1)-ből előállhat az I/a, I/b és I/c helyzet, (2)-ből a II. helyzet és (3)-ból a III. helyzet (6. ábra).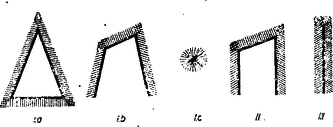
 
 
6. ábra
 

Az I/c eset (amidőn a 3 határegyenes egy pontban metszi egymást és így csak az egyetlen pont marad feladatunk értelmében fedetlen) az egyik félsíknak egy tetszésszerinti kis elhúzásával mindig visszavezethető az I/a esetre. Ugyanígy a III. helyzet is visszavezethető a II. helyzetre a közös határegyenessel bíró két félsíknak egy tetszésszerinti kicsiny széthúzásával. A negyedik félsík elhelyezésénél tehát már csak az I/a, I/b és II. esetekkel kell foglalkoznunk.
A fedetlen részeket teljesen lefedő negyedik félsík határegyenese vagy párhuzamos az első 3 sík valamelyikének határegyenesével vagy nem.
Ha párhuzamos, akkor az a félsík, melynek határegyenesével párhuzamos, a 4. félsíkkal együtt máris lefedi a teljes síkot.
Ha nem párhuzamos, akkor van az első 3 félsík által fedetlenül hagyott résznek egy szögpontja, mely a negyedik félsík határegyeneséhez a legközelebb fekszik. Ez esetben a 4. félsík azzal a két félsíkkal együtt, melyeknek határegyenesei a legközelebb fekvő szögpontban metszik egymást, nyilván teljesen lefedi a síkot (7. ábra).
 
 
7. ábra
 

II. megoldás: Ha tételünk nem volna igaz, akkor a négy lefedő félsík közül rendre egy-egy félsíkot elhagyva fedetlenül marad minden egyes alkalommal legalább egy-egy pont, ami azt jelenti, hogy van a síkban négy olyan pont: P1, P2, P3, P4 melyek mindegyike csak egyetlenegy félsíkkal van lefedve és ugyanakkor mindegyik félsik e 4 pont közül egy és csakis egy pontot fed le. Be fogjuk bizonyítani, hogy ilyen négy pont nem létezik.
 

Segédtétel: E négy pont közül három nem lehet egy egyenesen, mert az esetben a középső pont nem fedhető le egy félsíkkal úgy, hogy ugyanakkor a két szélső pont valamelyike ne kerüljön lefedésbe.
Marad tehát a 4 pont elhelyezésére a következő két eset:
a) Egy pont a másik három pont alkotta háromszögön belül van.
b) A négy pont egy konvex négyszöget alkot.
Az a) esetben jelöljük P4-gyel a belső pontot és messe a P3P4 egyenes a szemben fekvő P1P2 oldalt M-ben 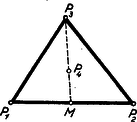(8. ábra).
 
 
8. ábra
 

Segédtételünk értelmében a P4-et lefedő félsíknak le kell fednie vagy a P3, vagy az M pontot is. Ugyancsak segédtételünkből következik, hogy minden M-et lefedő félsík P1 és P2 pontok valamelyikét lefedi. Így minden P4-et lefedő félsík szükségképpen lefed még legalább egy pontot P1, P2 és P3 közül.
b) esetben húzzuk meg a két átlót, ezek metszéspontja legyen M (9. ábra).
 
 
9. ábra
 

Segédtételünk értelmében minden M-et lefedő félsík fedi a P1P3 átló egyik végpontját, és ugyanakkor a P2P4 átló egyik végpontját is. Tehát minden M-et lefedő félsík legalább két P pontot fed le.
Ezzel tételünket bebizonyítottuk.
 

III. megoldás: Ha a 4 lefedő félsíkot két párban tekintjük, akkor feltehetjük, hogy egy-egy pár az I. megoldásban közölt (1) és (2) eset egyikét képviseli, mivel a (3) eset a (2)-re vezethető vissza.
Ha a két pár egyike a (2) esethez tartozik, akkor ‐ tekintve, hogy a két félsíkpár együtt lefedi az egész síkot ‐ az egyik pár által le nem fedett tartomány teljesen a síksáv egyik oldalán van és így a síksáv másik oldalát alkotó félsík elhagyható (lásd I. megoldás, 7. ábra).
Hátra van még az (1) ‐ (1) eset, vagyis amikor mindkét félsíkpár éket alkot. Itt ismét fennáll az, hogy ha két határegyenes (szögszár) párhuzamos, akkor e két határegyéneshez tartozó két félsík vagy lefedi a teljes síkot, vagy pedig e két félsík közül az egyik felesleges. Ha nincs párhuzamos határegyenes, akkor az egyik ék két félsíkjának elhúzásával (oly módon, hogy a mozgó félsíkok határegyenesei mindig párhuzamosak maradnak az eredeti határegyenesekkel) mindig elérhető az a helyzet, mikor a mozgó ék csúcspontja beleütközik a nyugvó ék egyik szárába (10/a ábra), vagy fordítva a mozgó ék egyik szára ütközik be a nyugvó ék csúcspontjába (10/b ábra).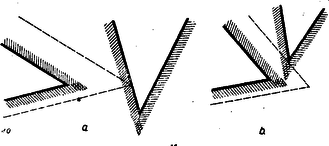
 
 
10. ábra
 

Mindkét esetben e csúcsponton átmenő 3 határegyeneshez tartozó 3 félsík már lefedi a teljes síkot, annál inkább áll fenn a lefedés a félsíkok visszatolása után. (Így bizonyította be a tételt a 2. díjnyertes, Kálmán Lajos.)
 

IV. megoldás: Ha egy egyenes véges számú félegyenessel teljesen le van fedve, akkor a félegyenesek két csoportba oszthatók aszerint, ahogy e félegyenesek a pozitív, illetőleg negatív irányban fedik le az egyenest a végtelenig. Mindegyik csoportba legalább egy félegyenes tartozik, mert véges számú egyirányú félegyenessel nem lehet egy egyenest teljesen lefedni. Ha az egyenest teljesen lefedő véges számú, pozitív irányú és negatív irányú félegyenesek közül kiválasztjuk azt az egy-egy félegyenest, mely az összes többi, vele egyirányú, félegyenest lefedi, akkor e 2 ellenkező irányú félegyenes már lefedi az egész egyenest. Tehát feladatunkban bármely félsík határegyenesét mindig 2 másik félsík már lefedi.
Most 3 esetet kell megkülönböztetni.
Ha a két lefedő félsík határegyenesei párhuzamosak egymással, akkor e két félsík már lefedi az egész síkot.
Ha a két lefedő félsík határegyeneseinek metszéspontja az első sík által lefedett tartományba esik, akkor ez a 3 félsík teljesen lefedi az egész síkot (11/a ábra).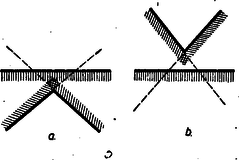
 
 
11. ábra
 

Végül, ha fenti metszéspont az első félsík által le nem fedett részbe esik, akkor az első félsík elhagyható (11/b ábra).
Megjegyzés: Ismeretes a koordináta geometriából, hogy ax+by+c=0 egy egyenes egyenlete. Minden x1, y1 számpárnak, melyre nézve ax1+by1+c=0, megfelel egy pont az egyenesen. Viszont, ha az ax1+by1+c>0, akkor x1, y1 pont az ax+by+c=0 egyenesnek azon az oldalán van, amelyen az origo, ha c>0, és ellenkező oldalán, ha c<0. Ez azt jelenti, hogy mindazon pontok összessége, melyek kielégítik az ax+by+c>0 egyenlőtlenséget, egy félsík belső pontjai, mely félsíknak határegyenese az ax+by+c=0 egyenes.
Ezek szerint most már bebizonyított tételünk így is fogalmazható:
Ha az alábbi négy egyenlőtlenségre
a1x+b1y+c1>0a2x+b2y+c2>0a3x+b3y+c3>0a4x+b4y+c4>0


fennáll, hogy bármilyen x, y számpár legalább egy egyenlőtlenséget kielégít, akkor mindig található a négy egyenlőtlenség között egy olyan, melyet elhagyva, az előbbi állítás a megmaradó három egyenlőtlenségre is fennáll. E tétel közvetlen bizonyítása nem volna egyszerű.