Kezdőlap


Cím:	A szabályos ötszög szerkesztéséhez
Szerző(k):	Hódi Endre
Füzet:	1952/május, 110 - 113. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A II. gimn. matematikakönyv 146. oldalán utalás történik arra, hogy a szabályos tízszög szerkesztésében fellépő körív húrja éppen az ugyanebbe a körbe írható szabályos ötszög egy oldala (1. ábra). Ezt fogjuk igazolni a következőkben.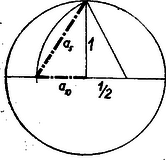

1. ábra

Bizonyításunkban egységsugarú kört használunk; ez nem megy az általánosság rovására, mert ha a kör sugara

r

egység volna, a bele rajzolt ,,húrok'' és egyéb ugyanolyan módon szerkesztett szakaszok is mind

r

-szeresükre növekednének (csökkennének) a hasonlóság folytán, ennélfogva arányuk változatlan marad.

Tudnunk kell, hogy az egységsugarú körbe rajzolható szabályos tízszög

a_{10}

oldala eleget tesz az

\begin{matrix} 1 = a_{10} (a_{10} + 1) \end{matrix}

másodfokú egyenletnek. (L. a II. gimn. matematikakönyv 144. oldalán. Ott ilyen alakban fordul elő:

\begin{matrix} R^{2} = a (a + R) . \end{matrix}

R = 1

, és

a

helyett

a_{10}

-et írunk, akkor előbbi egyenletünkhöz jutunk.)

a_{10}

értéke ebből az egyenletből ki is számítható:

\begin{matrix} a_{10} = \frac{\sqrt[]{5} - 1}{2}, \end{matrix}

mert a negatív gyöknek,

- \frac{\sqrt[]{5} + 1}{1}

-nek itt nem tudunk geometriai jelentést tulajdonítani.
A nem gimnazisták részére itt közöljük az

a_{10}

-re vonatkozó fenti egyenlet egy bizonyítását.
Tekintsük az egységsugarú körbe írt szabályos tízszög egyik középponti háromszögét (2. ábra).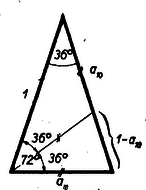

2. ábra

A két vonalkával áthúzott szakaszok ‐ a szereplő háromszögek egyenlő szárú volta miatt ‐ mind egyenlők

a_{10}

-zel. Az eredeti és az alsó kis háromszög hasonlósága miatt (szögeik megegyeznek):

\begin{matrix} (1 - a_{10}) : a_{10} = a_{10} : 1, \end{matrix}

vagyis

a_{10}

az aranymetszés szerint osztott egységnyi sugár nagyobbik darabja.
A beltagok szorzata egyenlő a kültagok szorzatával:

\begin{matrix} a_{10}^{2} = 1 - a_{10}, amiből 1 = a_{10} (a_{10} + 1), \end{matrix}

vagyis megkaptuk a fenti másodfokú egyenletet.
Az egységtávolság aranymetszés szerinti osztását a 3. ábra mutatja.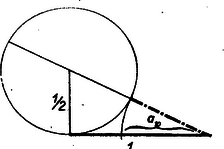

3. ábra

Az egységtávolság egyik végpontjában félegység sugarú érintőkört szerkesztünk az egységtávolsághoz. Ezen kör középpontján és az egységtávolság másik végpontján átmenő szelőn keletkező két metszet

a_{10}

és

a_{10} + 1

. Igazolás: Egy pontból húzott érintő (ábránkban az egységtávolság) mértani középarányos az ugyanabból a pontból húzott szelő két metszete között, vagyis

\begin{matrix} 1 = a_{10} (a_{10} + 1) . \end{matrix}

Látjuk, hogy

a_{10}

-et úgy kapjuk, hogy

1

és

^{1} /_{2}

egységnyi befogókkal bíró derékszögű háromszög átfogójából kivonjuk a kisebbik befogót, az

^{1} /_{2}

-et. Ez történik az

a_{10}

-nek szokásos szerkesztésénél is. (L. 1. ábrát.)
Visszatérve cikkünk tulajdonképpeni tárgyára, azt fogjuk bizonyítani, hogy az egységsugarú körbe szerkeszthető szabályos ötszög

a_{5}

oldala és a szabályos tízszög

a_{10}

oldala között az

\begin{matrix} a_{5}^{2} = 1 + a_{10}^{2} \end{matrix}

összefüggés áll fenn. Ez nyilvánvalóan ugyanaz, mint amit először állítottunk, mert hiszen a szabályos tízszög szerkesztésével kapcsolatban említett húr olyan derékszögű háromszög átfogója, amelynek befogói az egységnyi sugár és

a_{10}

, tehát ennek a húrnak a négyzete Pythagoras tétele értelmében

1 + a_{10}^{2}

-tel egyenlő. Ha most sikerül kimutatnunk, hogy

a_{5}

négyzete is ugyanennyi, akkor ezek, vagyis a szóbanforgó húr és

a_{5}

maguk is egyenlők (hiszen mindketten pozitívok), ennélfogva a szóbanforgó húr csakugyan a szabályos ötszög egy oldala.
Állításunk igazolását kétféleképpen: elemi úton és trigonometriai ismeretek felhasználásával is végezzük, hogy alkalom kínálkozzék a különböző módszerek összehasonlítására.
a) Az elemi geometriai eljárás során először is összefüggést állapítunk meg ugyanabba az egységnyi sugarú körbe szerkeszthető szabályos (konvex)

n

-szög és

2 n

-szög oldalának hosszúsága között. (4. ábra.).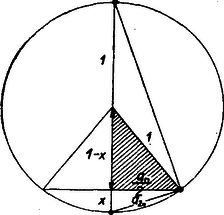

4. ábra

A megvastagított csúcsú (Thales tétele szerint) derékszögű háromszögben mint az egyik befogó, mértani közepe az átfogónak (a kör átmérőjének) és az erre eső vetületének, amit

x

-szel jelöltünk. Eszerint:

\begin{matrix} a_{2 n}^{2} = 2 x . \end{matrix}

A bevonalkázott derékszögű háromszögre Pythagoras tételét alkalmazva:

\begin{matrix} {(1 - x)}^{2} + {(\frac{a_{n}}{2})}^{2} = 1, \end{matrix}

ebből

1 - x = \sqrt[]{1 - \frac{a_{n}^{2}}{4}}

, illetőleg

1 - x = \sqrt[]{1 - \frac{a_{n}^{2}}{4}}

x

értékét

a_{2 n}^{2} = 2 x

egyenletünkbe írva:

\begin{matrix} a_{2 n}^{2} = 2 (1 - \sqrt[]{1 - \frac{a_{n}^{2}}{4}}) = 2 - \sqrt[]{4 - a_{n}^{2}} . \end{matrix}

Speciálisan, ha

n = 5

\begin{matrix} a_{10}^{2} = 2 - \sqrt[]{4 - a_{5}^{2}} \end{matrix}

Ezt szeretnők a kívánt

a_{5}^{2} = 1 + a_{10}^{2}

alakra hozni. Felhasználjuk e célból, hogy

a_{10}

eleget tesz a cikkünk elején említett

\begin{matrix} 1 = a_{10} (a_{10} + 1) \end{matrix}

egyenletnek. Ebből

\begin{matrix} a_{10}^{2} = 1 - a_{10}, \end{matrix}

s ezt utolsó négyzetgyökös egyenletünkbe írva:

\begin{matrix} 1 - a_{10} = 2 - \sqrt[]{4 - a_{5}^{2}}, azaz \sqrt[]{4 - a_{5}^{2}} = 1 + a_{10} . \end{matrix}

Távolítsuk el a négyzetgyököt:

\begin{matrix} 4 - a_{5}^{2} = 1 + 2 a_{10} + a_{1}^{2} \end{matrix}

Az itt még fölösleges

2 a_{10}

tagot ismét az

\begin{matrix} 1 = a_{10} (a_{10} + 1) illetőleg a_{10} = 1 - a_{10}^{2} \end{matrix}

összefüggés alapján helyettesítjük megfelelővel:

\begin{matrix} 4 - a_{5}^{2} = 1 + 2 (1 - a_{10}^{2}) + a_{10}^{2} . \end{matrix}

Ha utolsó egyenletünkben polinommá alakítunk, összevonás és rendezés után csakugyan a kívánt

\begin{matrix} a_{5}^{2} = 1 + a_{10}^{2} \end{matrix}

összefüggéshez jutunk.

b) A trigonometriai igazolásban az egységsugarú körbe írható szabályos ötszög egy középponti háromszögéből indulhatunk ki (5. ábra).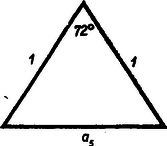

5. ábra

Írjuk fel erre a cosinus-tételt:

\begin{matrix} a_{5}^{2} = 1 + 1 - 2 cos 72^{\circ} = 1 + 1 - 2 sin 18^{\circ} . \end{matrix}

A szabályos

n

-szög egyik középponti háromszögét a csúcsnál lévő szög felezőjének meghúzásával két egybevágó derékszögű háromszögre osztjuk.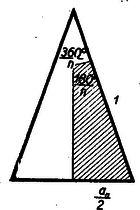

6. ábra

Ezek egyikéből (a 6. ábrán bevonalkáztuk) a szabályos

n

-szög oldala,

a_{n}

a következő módon számítható ki (A körülírt kör sugarát most is egységnyinek vesszük.):

\begin{matrix} \frac{a_{n}}{2} = sin \frac{180^{\circ}}{n}, azaz a_{n} = 2 sin \frac{180^{\circ}}{n} . \end{matrix}

Speciálisan, ha

n = 10

\begin{matrix} a_{10} = 2 sin 18^{\circ}, \end{matrix}

fentebbi egyenletünk ennélfogva így alakul:

\begin{matrix} a_{5}^{2} = 1 + 1 - a_{10} . \end{matrix}

De már láttuk (az elemi megoldás során), hogy

\begin{matrix} 1 - a_{10} = a_{10}^{2}, \end{matrix}

vagyis csakugyan

\begin{matrix} a_{2}^{5} = 1 + a_{10}^{2} . \end{matrix}

Említettük, hogy

a_{10} = \frac{\sqrt[]{5} - 1}{2}

, ennek és utolsó egyenletünknek alapján most már

a_{5}

értéke is kiszámítható.