Kezdőlap


Cím:	Az 1952. évi Arany Dániel matematikai verseny
Füzet:	1952/október, 33 - 41. oldal	PDF \| MathML
Témakör(ök):	Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A Középiskolai Matematikai Lapok szerkesztősége, a Bolyai János Matematikai Társulat és a Közoktatásügyi Minisztérium támogatásával ez évben április 26-án és május 25-én rendezte az Arany Dániel matematikai tanulóversenyt. Ezúttal csak az I ‐ II. osztályosok részére, tekintettel arra, hogy a III ‐ IV. osztályosok a Rákosi Mátyás tanulmányi versenyen vettek részt. Az első forduló feladatai a következők voltak:
1. Adva van egy távolság, egy kör és ennek belsejében a $P$ pont. Szerkesztendő az adott körnek olyan $A B$ húrja, mely a $P$ ponton áthalad és amelyre vonatkozóan az $A P$ és $B P$ szakaszok különbsége az adott távolsággal egyenlő.
2. Hozzuk legegyszerűbb alakra az

\begin{matrix} \frac{{(x^{2} - y^{2})}^{3} + {(y^{2} - z^{2})}^{3} + {(z^{2} - x^{2})}^{3}}{{(x - y)}^{3} + {(y - z)}^{3} + {(z - x)}^{3}} . \end{matrix}

kifejezést.
3. Egy üzemben 40 munkás sztahanovista munkamódszerre tér át. Ezáltal az üzem termelése 20%-kal emelkedik. Ha az első sztahanovistákkal együtt a munkásoknak összesen 60%-a tér át az új munkamódszerre, akkor ezáltal az üzem termelése az eredeti termelésnek két és félszeresére növekszik. Kérdés, hány munkás van az üzemben és hányszorosra emelkedik az üzem termelése, ha valamennyi munkás megtanulja az új munkamódszert?
A beérkezett 3000-en felüli dolgozatból a kerületi bizottságok javaslatát figyelembe véve 358-an jutottak a második fordulóba. A második forduló feladatai a következők voltak:
1.

A

és

B

5000 méteres távon versenyt futnak. Az első kísérletnél

A

1 km előnyt ad

B

-nek és 1 perccel előbb ér célba. A második kísérletnél

A

8 perc előnyt ad és 1 km-re van még a céltól, mikor

B

célba ér. Hány perc alatt futja be

A

és mennyi alatt

B

az 5000 méteres távot? (Feltesszük, hogy a két versenyben nem változik a futók átlagsebessége.)
2. Bizonyítsuk be, hogy bármilyen egész szám is

n

\begin{matrix} n (n + 2) (5 n - 1) (5 n + 1) \end{matrix}

mindig osztható 24-gyel.
3. Szerkesszünk háromszöget, ha adott a háromszög köré írt kör sugara; az oldalakat belülről érintő kör sugara és a háromszög egyik szöge.

A Központi bizottság, amelynek tagjai voltak: Aczél Istvánné minisztériumi főelőadó, Hajós György Kossuth-díjas egyetemi tanár, Lőrincz Pál műegyetemi adjunktus, Neukomm Gyula felelős szerkesztő, Varga Tamás egyetemi tanársegéd, és Surányi János egyetemi docens, főszerkesztő, mint előadó, a következőket állapította meg:
A döntőben 335 versenyző indult. Beadta dolgozatát Budapestem 194 versenyző közül 163, Szegeden 27 versenyző közül 27, Debrecenben 21 versenyzőből 15, Miskolcon 18 versenyző közül 12, Pécsett 11 versenyző közül 11, Veszprémben 19 versenyző közül 19, Győrött 35 versenyző közül 35, és Egerben l0 versenyző közül 10. Összesen tehát beadtak 292 dolgozatot. 12 versenyző oldotta meg mindhárom feladatot, további 15-en foglalkoztak érdemben mindhárom feladattal, de nem mindenre adtak teljes megoldást, vagy csak két feladatot oldottak meg, de valamelyiket kiemelkedően ügyesen. Ennyiben a verseny páratlanul sikeres volt. Nem mutatott azonban ilyen kedvező képet a döntő dolgozatainak egésze. A dolgozatok igen nagy hányada egyetlen feladat megoldását sem tartalmazta, vagy csak a legkönnyebb első feladatét. Egyes kerületekben a döntőben beadott összes dolgozat ilyen volt. Általában feltűnő a vidék óriási lemaradása a pesti versenyzőkkel szemben, különösen az ez irányban az előző évek folyamán bekövetkezett erős javulás után. Összesen 6 vidéki tanuló szerepel az említett 27 közt. Hasonlóan kedvezőtlen tünetnek kell tekinteni azt a tényt is, hogy összesen egy ipari technikumi tanuló szerepel a javaslandók közt, annak ellenére, hogy ennek az iskolatípusnak kevéssel tér el a matematikai tanterve az általános gimnáziumétól.
A már említett 12 dolgozat közül, melyek mindhárom feladat megoldását tartalmazzák, öt emelkedik különösen ki.
Vigassy József dolgozatában különösen a harmadik feladat megoldása értékes. Erre két különböző megoldást ad és jelzi a megoldhatóság feltételének megkereséséhez vezető utat, bár azt nem követi számítással. A második feladatnak is két megoldását adja, bár maga is jelzi, hogy azok nem különböznek lényegesen.
Kovács László a második feladatra két lényegesen különböző megoldást ad, ügyesen kezeli az első feladatot is. A harmadiknál pontosan megadja a szerkeszthetőség feltételét,
A Bizottság Kovács Lászlónak a debreceni Református Kollégium gimnáziuma II. o. tanulójának és Vigassy József a budapesti I. ker. Petőfi gimnázium II. o. tanulójának egy-egy I. Arany Dániel díjat ítélt oda.
Schmidt Eligius dolgozata ugyancsak két megoldást tartalmaz a második feladatra, a harmadik feladatnál pedig tárgyalja a megoldhatóság feltételét. Az első feladat megoldása kissé hosszadalmas nála. A Bizottság Schmidt Eligius, a budapesti II. kerületi Fürst Sándor gimnázium II. o. tanulójának dolgozatát II. Arany Dániel díjjal jutalmazza.
Reichlin Viktor dolgozata a második feladatnak két, de nem lényegesen különböző megoldását tartalmazza. A harmadik feladatnál keresi a megoldhatóság feltételét, de egy tévesen felírt összefüggés alapján hibás eredményre jut.
Fábián Egon dolgozatában a harmadik feladatra ad kétféle megoldást, hivatkozva az első gimnázium tankönyvének egy rokon feladatára. A Bizottság Reichlin Viktor, a budapesti V. ker. Piarista gimnázium II. o. tanulójának dolgozatát és Fábián Egon, a budapesti XI. ker. József Attila gimnázium II. o. tanulójának dolgozatát I. dicséretben részesíti.
II. dicséretet nyert a következő hét tanuló, akik lényegében szintén megoldották mindhárom feladatot: Bártfai Pál budapesti ref. gimn. I. o. tanulója, Eördögh László budapesti Apáczai Csere János gimn. II. o. tanulója, Grätzer György budapesti Berzsenyi Dániel gimn. II. o. tanulója, Kertész Ádám budapesti Fürst Sándor gimn. I. o. tanulója, Kovács Ferenc budapesti Piarista gimn. II. o. tanulója, Lőw Miklós budapesti Vörösmarty Mihály gimn. II. o. tanulója, Zawadowsky Alfréd budapesti Petőfi Sándor gimn. II. o. tanulója.
A Bizottság további 15 dolgozat szerzőjét III. dicséretben részeseti. Ezek a következők: Balatoni Ferenc budapesti II. Rákóczi Ferenc közg. középiskola II. o., Beleznay Ferenc budapesti Piarista gimn. I. o., Bódás Péter székesfehérvári József Attila gimn. II. o., Botár László miskolci Földes Ferenc gimn. II. o, Gergely József keszthelyi ált. gimn. II. o., Huszár Károly budapesti Rákóczi Ferenc gimn. II. o., Legéndi Károly budapesti, református gimn. II. o., Paál Zoltán budapesti, Könyves Kálmán gimn. II. o., Pátkai Győrgy budapesti Fáy András gimn. I. o., Roboz Ágnes budapesti Varga Katalin gimn. I. o., Sántha Ernő budapesti Fáy András gimn. I. o., Szerdahelyi Jenő miskolci XIII. sz. Gépipari Technikum II.o., Tahy Péter budapesti II. Rákóczi Ferenc gimn. II. o., Tomor Benedek győri Révai gimn. II. o., Uray László budapesti Piarista gimn. I. o. tanuló.
Alábbiakban közöljük a kitűzött feladatok megoldásait.

Az I. forduló feladatai

1. feladat.

I. megoldás: Képzeljük a feladatot megoldottnak. Jelöljük az adott kör középpontját

O

-val és az adott

A P - P B

távolságot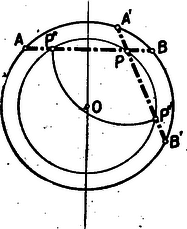

d

-vel.

1. ábra

A keresett

A B

húrra merőleges átmérő ‐ egy megoldást tekintve ‐ az ábra szimmetria tengelye. Ha az

A B

húron

A

pontbál felmérjük a

P B = A P^{*}

távolságot, akkor az így nyert

P^{*}

pont nyilván a

P

pont tükörképe a fenti átmérőre nézve és

A P - P B = A P - A P^{*} = P^{*} P = d

(1: ábra).
Eszerint a szerkesztés menete: az

O

körül

P O

sugárral rajzolt koncentrikus körben megszerkesztjük a

P P^{*} = P P^{*} = d

húrokat. E húrok meghosszabbításai adják az

A B

és

A' B'

megoldásokat.
A megoldások száma 2, 1, 0 aszerint, amint

d ⋚ 2 \cdot O P

. Ha

d = 0

, akkor a két megoldás egybeolvad az

O P

-re merőleges húrrá.

II. megoldás: Jelölés mint az I. megoldásban. A

P P^{*}

felezőpontja

F

egyszersmind az

A B

felezőpontja, tehát

O F ⊥ F P

és így az

F

pont rajta van az

O P

fölé, mint átmérö fölé rajzolt Thales-körön, továbbá

P F = P F' = \f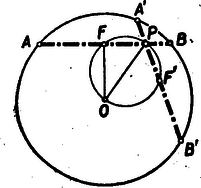rac{d}{2}

. (2. ábra).

2. ábra

A megoldhatóság feltétele, hogy

\frac{d}{2} ≦ O P

, ami megegyezik az I. megoldásban talált eredménnyel.
Többen azzal próbálkoztak, hogy

B P

-t az

A P

-ből a

P

-től számítva mérték vissza. Így mértani helyül a kör

P

-re vonatkozó centrális tükörképét kapták. Ezzel azonban nehezebb feladathoz jutottak: két egyenlő sugarú, egymást metsző kör közös húrjának felezőpontján át olyan szelőt húzni, melynek az adott körök különböző ívei közé eső szakasza adott hosszúságú.

2. fetadat.
I. megoldás: Az

u^{3} + v^{3} = (u + v) (u^{2} - u v + v^{2})

azonosság alapján törtünk nevezője

\begin{matrix} {(x - y)}^{3} + {(y - z)}^{3} + {(z - x)}^{3} = \\ = & (x - y + y - z) [{(x - y)}^{2} - (x - y) (y - z) + {(y - z)}^{2}] + {(z - x)}^{3} = \\ = & (x - z) [(x - y) (x - y - y + z) + {(y - z)}^{2} - {(z - x)}^{2}] = \\ = & (x - z) [(x - y) (x - 2 y + z) + (y - z + z - x) (y - z - z + x)] = \\ = & (x - z) [(x - y) (x - 2 y + z) - (x - y) (y - 2 z + x)] = \\ = & (x - z) (x - y) (x - 2 y + z - y + 2 z - x) = \\ = & (x - z) (x - y) (3 z - 3 y) = 3 (x - y) (y - x) (z - x) . \end{matrix}

Hasonlóképpen a számláló

\begin{matrix} {(x^{2} - y^{2})}^{3} + {(y^{2} - z^{2})}^{3} + {(z^{2} - x^{2})}^{3} = 3 (x^{2} - y^{2}) (y^{2} - z^{2}) (z^{2} - x^{2}) \end{matrix}

Az adott tört tehát

\begin{matrix} \frac{3 (x^{2} - y^{2}) (y^{2} - x^{2}) (z^{2} - x^{2})}{3 (x - y) (y - z) (z - x)} = (x + y) (y + z) (z + x) . \end{matrix}

II. megoldás: Tekintsük a nevezőt

x

polinomjaként. A polinommá átalakítás tényleges elvégzése nélkül is könnyen látható, hogy másodfokú polinomot kapunk, mert az első és harmadik kifejezésből adódó

x^{3}

-os tagok összege 0-t ad. Ennek a polinomnak 0 helyei

x = y

és

x = z

, ami behelyettesítéssel azonnal látható. Így a nevező gyöktényezős előállítása azonos az

(x - y) (x - z)

szorzatnak és az

x^{2}

-es tag együtthatójának szorzatával. Az első és harmadik kifejezésből

x^{2}

együtthatója

- 3 y + 3 z = 3 (z - y)

; tehát a nevező azonos a

\begin{matrix} 3 (x - y) (x - z) (z - y) \end{matrix}

szorzattal. Ebből megkapjuk a számlálót, ha

x

y

z

helyett

x^{2}

y^{2}

z^{2}

-et írunk, tehát a keresett tört:

\begin{matrix} \frac{3 (x^{2} - y^{2}) (x^{2} - z^{2}) (z^{2} - y^{2})}{3 (x - y) (x - z) (z - y)} = (x + y) (y + z) (z + x) . \end{matrix}

III. megoldás: A számláló és nevező olyan három szám köbének összege, amely három szám összege 0. Ha pedig

a + b + c = 0

, akkor kimutatható, hogy

\begin{matrix} a^{3} + b^{3} + c^{3} = 3 a b c \end{matrix}

Ugyanis, ha

\begin{matrix} a + b = - c \end{matrix}

akkor köbre emelve

\begin{matrix} a^{3} + 3 a^{2} b + 3 a b^{2} + b^{2} = - c^{3} \end{matrix}

vagyis

\begin{matrix} a^{3} + b^{3} + c^{3} = - 3 a b (a + b) = - 3 a b (- c) = 3 a b c . \end{matrix}

E segédtétel egyébként közvetlenül adódik a következő azonosságból is:

\begin{matrix} a^{3} + b^{3} + c^{3} - 3 a b c = (a + b + c) (a^{2} + b^{2} + c^{2} - a b - b c - c a) \end{matrix}

Ennek alapján kifejezésünk így írható:

\begin{matrix} \frac{3 (x^{2} - y^{2}) (y^{2} - z^{2}) (z^{2} - x^{2})}{3 (x - y) (y - z) (z - x)} = (x + y) (y + z) (z + x) . \end{matrix}

3. feladat.
I. megoldás: Legyen egy sztahanovista túltermelése a régi módszerrel termelő munkás termelésének

x

-szerese és a munkások száma

y

. Akkor a feladat szerint

\begin{matrix} y + 40 x = 1, 2 y \end{matrix}

(1)

és

\begin{matrix} y + 0, 6 y x = 2, 5 y . \end{matrix}

(2)

\begin{matrix} (2) - ből x = \frac{2, 5 - 1}{0, 6} = \frac{1, 5}{0, 6} = 2, 5 \end{matrix}

x

ezen értékét (1)-be helyettesítve

\begin{matrix} y + 100 = 1, 2 y, \end{matrix}

amiből

y = 500

munkás

és az üzem termelése, ha valamennyi munkás áttér az új munkamódszerre;

1 + x = 3, 5

-szörösre (350%-ra) emelkedik.

II. megoldás: Egy sztahanovista túltermelése az üzem össztermelésének

\frac{20}{40} = \frac{1}{2} %

-a. A munkások 60%-ának túltermelése a feladat szerint az össztermelésnek 150%-a, amiből következik, hogy a munkások

60 %

-a

(150 :^{1} /_{2} =)

300 munkást jelent, vagyis a munkások összlétszáma 500 és így a túltermelés, ha mind az 500 munkás sztahanovistává válik,

500 \cdot^{1} /_{2} = 250 %

, vagyis az üzem termelése 3,5-szeresre emelkedik.

A II. forduló feladatai,

1. feladat.
I. megoldás: A

x

perc alatt.

B

y

perc alatt tesz meg 1 km-t.
Az első kisérletnél A

5 x

perc alatt 5 km-t,

B

pedig 1 perccel hosszabbidő alatt 4 km-t tesz meg,
tehát

5 x + 1 = 4 y

. (1)

A második kísérletnél

B

5 y

perc alatt fut be 5 km-t, míg

A

8 perccel rövidebb idő alatt 4 km-t,
tehát

5 y - 8 = 4 x

vagyis

4 x + 8 = 5 y

. (2)

(2)-ből (1)-et kivonva

\begin{matrix} y = 7 - x . \end{matrix}

y

ezen értékét (1)-be helyettesítve

\begin{matrix} 5 x + 1 = 28 - 4 x, \end{matrix}

amiből

x = 3 és így y = 7 - x = 4

.
Tehát az 5000 m-es távot

A

15,

B

20 perc alatt futja be.

II. megoldás: A 5 km-t

x

perc alatt, tehát 1 km-t

\frac{x}{5}

perc alatt fut be.
Az első kísérletnél

B

4 km-t

(x + 1)

perc alatt tesz meg, tehát 1 km-t

\frac{x + 1}{4}

perc alatt.
A második kísértetnél

B

5 km-t

\frac{5 (x + 1)}{4}

perc alatt,

A

pedig 4 km-t

\frac{4 x}{5}

perc alatt fut be és a feladat szerint

\begin{matrix} \frac{5 (x + 1)}{4} = \frac{4 x}{5} + 8, \end{matrix}

amiből

x = 15

perc.

B

ideje 5 km-re pedig

\frac{5 (x + 1)}{4} = 20

perc.

III. megoldás: A két futamban együttesen mindkét versenyző 9 km-t tesz meg, de

A

9 perccel rövidebb ideig fut.
Tehát A 1 km-t 1 perccel rövidebb idő alatt tesz meg, mint

B

. Az első versenyen

A

így 4 km-en 4 perc előnyt szerez és mivel 1 perccel győz, az első km megtétele 3 percig tart,

B

tehát 4 perc alatt tesz meg 1 km-t. Vagyis

A

15 percig,

B

20 percig fut 5 km-t.

2. feladat.

I. megoldás: a) Ha

n

3-mal osztható, akkor nyilvánvaló, hogy szorzatunk is osztható 3-mal. Ha

n

3-mal nem osztható, akkor

5 n

sem osztható 3-mai, és így

5 n - 1

és

5 n + 1

közül az egyik osztható 3-mal, mert három egymásután következő szám:

5 n - 1

5 n

5 n + 1

közül az egyik feltétlenül osztható 3-mal.
b) Ha

n

páros, akkor

n

és

n + 2

, ha pedig

n

páratlan, akkor

5 n - 1

és

5 n + 1

két egymás után következő páros szám. Két egymásután következő páros szám közül az egyik mindig osztható 4-gyel és így szorzatunk mindig osztható

2 \cdot 4 = 8

-cal.
Mind a), mind b) alatt az összes lehetséges eseteket kimerítettük és így bebizonyítottuk, hogy szorzatunk

n

minden egész számú értéke mellett osztható 3-mal is és 8-cal is, mivel pedig e két számnak nincs közös osztója, tehát a szorzatukkal

3 \cdot 8 = 24

-gyel is.

II. megoldás: Teljes indukció is célra vezet.

n = 1

-re

1 \cdot (1 + 2) (5 - 1) (5 + 1) = 3 \cdot 24

osztható 24-gyel.
Tegyük fel, hogy valamilyen

n = k

értékre már igazoltuk az állítás helyességét, azaz

\begin{matrix} k (k + 2) (5 k - 1) (5 k + 1) = 25 k^{4} + 50 k^{3} - k^{2} - 2 k = 24 A, \end{matrix}

ahol

A

valamilyen egész szám.

k

helyébe

(k + 1)

-et téve:

\begin{matrix} (k + 1) (k + 3) (5 k + 4) (5 k + 6) = 25 k^{4} + 150 k^{3} + 299 k^{2} + 246 k + 72 = \\ = & 100 k^{3} + 300 k^{2} + 248 k + 72 + 25 k^{4} + 50 k^{3} - k^{2} - 2 k = \\ = & 24 (4 k^{3} + 12 k^{2} + 10 k + 3) + 4 k^{3} + 12 k^{2} + 8 k + 24 A = \\ = & 24 B + 4 k (k^{2} + 3 k + 2) + 24 A = \\ = & 24 (A + B) + 4 k (k + 1) (k + 2) \end{matrix}

Mivel

k (k + 1) (k + 2)

, mint 3 egymásra következő szám szorzata osztható

2 \cdot 3 = 6

-tal, azért a nyert kéttagú összegünk második tagja is osztható

4 \cdot 6 = 24

-gyel. Tehát ha tételünk

n = k

-ra igaz, akkor

n = (k + 1)

-re is igaz, de

n = 1

-re igaz és így minden

n

egész számra fennáll.

III. megoldás:

\begin{matrix} n (n + 2) (5 n - 1) (5 n + 1) = n (n + 2) (25 n^{2} - 1) = \end{matrix}

\begin{matrix} = n (n + 2) [24 n^{2} + (n 2 - 1)] = 24 n^{3} (n + 2) + (n - 1) n (n + 1) (n + 2) . \end{matrix}

Az első tag nyilván osztható 24-gyel, a második tag pedig 4 egymásra következő szám szorzata. Ezek közt van mindig 3-mal osztható és van két egymásutáni páros tényező, melyek közül valamelyik így 4-gyel is osztható. Szorzatunk tehát osztható

3 \cdot 2 \cdot 4 = 24

-gyel.

A versenyzők legnagyobb része diszkusszióval (I. megoldás) oldotta meg a feladatot, de gyakran nagyon hosszadalmasan. Volt olyan versenyző is, aki

n

-nek 24-gyel való osztásából adódó teljes

0

1

2 ...

, 23 maradéksorra külön-külön bizonyított.

3. feladat.

I. megoldás: Képzeljük a feladatot megoldottnak. Legyen az adott szög

α

a háromszög köré írt kör középpontja

K

és sugara

r

, beírt kör középpontja

O

és sugara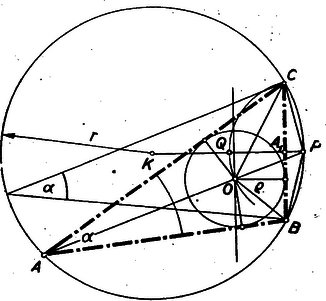

ϱ

. (1. ábra).

1. ábra

B O C ▵

-ből

B O C ∢ = 180^{\circ} - \frac{β}{2} - \frac{γ}{2} = \frac{360^{\circ} - (β + γ)}{2} = \frac{180^{\circ} + [180^{\circ} - (β + γ)]}{2} = \frac{180^{\circ} + α}{2} = 90^{\circ} + \frac{γ}{2}

.
A kerületi szögek tétele alapján a

K

középpontú és

r

sugarú körben tetszőleges a kerületi szög szárainak a körrel való metszéspontjai megadják a háromszög

B C = a

oldalát.
Az

O

pont ‐ a fentiek szerint ‐ rajta van azon a

B C

köríven, melynek pontjaiból a

B C

távolság

90 + \frac{α}{2}

szög alatt látszik és amely körív a

B C

oldalnak ugyanazon az oldalán van, mint az

α

szög csúcspontja. E látószög-kör középpontját

P

-vel jelölve, a központi és kerületi szög közötti összefüggés alapján

\begin{matrix} B P C ∢ = 360^{\circ} - 2 (90 + \frac{α}{2}) = 180^{\circ} - α, \end{matrix}

(1)

vagyis az

A B P C

négyszög húrnégyszög és így a

P

pont a

B C

ív felezőpontja.
Egy másik geometriai hely

O

-ra nézve a

B C

egyenestől

ϱ

távolságban a

B C

-vel párhuzamosan húzott egyenes, a

B C

egyenesnek ugyanazon az oldalán, mint az előbbi körív.
A két mértani hely egyik metszéspontja a keresett

O

pont.

O

körül

ϱ

sugárral rajzolt körhöz a

B

és

C

pontokból szerkesztett érintők metszéspontja

A

(amely rajta van a köré írt körön) a keresett háromszög harmadik csúcspontja. (Általában két pontot kapunk

O

számára, de mindkettő egybevágó háromszögekre vezet, tehát csak egy megoldásról beszélünk.)
Határozzuk meg a megoldhatóság feltételeit. Jelöljük az

a

oldal felezőpontját

A_{1}

-gyel és a

P A_{1}

egyenesnek metszéspontját a látószög-körívvel,

Q

-val. Megoldás nyilván csak akkor van, ha

ϱ ≦ A_{1} Q

Mivel (1) alapján az

A_{1} B P ∢ = \frac{α}{2}

, azért

\begin{matrix} A_{1} P = \frac{a}{2} tg \frac{α}{2} = \frac{a sin \frac{α}{2}}{2 cos \frac{α}{2}} \end{matrix}

és

\begin{matrix} P Q = P B = \frac{a}{2 cos \frac{α}{2}} \end{matrix}

amiből

\begin{matrix} A_{1} Q = P Q - A_{1} P = \frac{a}{2 cos \frac{α}{2}} - \frac{a sin \frac{α}{2}}{2 cos \frac{α}{2}} = \frac{a (1 - sin \frac{α}{2})}{2 cos \frac{α}{2}} . \end{matrix}

\begin{matrix} De a = 2 r sin α = 4 r sin \frac{α}{2} cos \frac{α}{2} \end{matrix}

\begin{matrix} és így A_{1} Q = 2 r sin \frac{α}{2} (1 - sin \frac{α}{2}) . \end{matrix}

Tehát megoldás csak akkor van, ha

\begin{matrix} ϱ ≦ 2 r sin \frac{α}{2} (1 - sin \frac{α}{2}) \end{matrix}

Egyenlőség esetén

ϱ = A_{1} Q

és a háromszög egyenlő szárú

(b = c)

.
Állandó

r

esetén a jobboldal akkor [maximális, ha

sin \frac{α}{2} (1 - sin \frac{α}{2})

maximális. Egy szorzat pedig, amelyben a tényezők összege állandó, akkor veszi fel a legnagyobb értéket, ha a tényezők egyenlők, vagyis

sin \frac{α}{2} = \frac{1}{2}

, amiből

a = 60^{\circ}

és

ϱ ≦ \frac{r}{2} \cdot ϱ

maximális értéke tehát

\frac{r}{2}

és ezt akkor veszi fel, ha

a = 60^{\circ}

és azonkívül

β = γ = 60^{\circ}

, vagyis a háromszög egyenlő oldalú. L. >>K. M. L<< I. évf. 1948. május , 167. sz. feladat.)

II. megoldás: Felhasználjuk ezt a tételt (I. osztályos tankönyv 1950‐es kiadás, 285. oldal), mely szerint egy háromszög beírt és hozzáírt körének egy-egy közös külső érintő oldalon lévő két érintési pontjának távolsága egyenlő a harmadik oldallal, amely a fenti két kör közős belső érintőjének a külső érintők közé eső szakasza.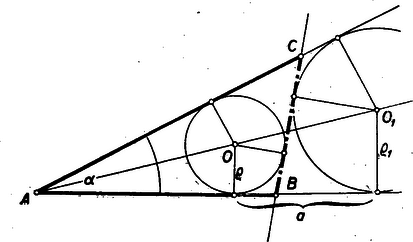

2. ábra

Eszerint a szerkesztés menete: a

B C = a

háromszög oldal szerkesztése ugyanúgy történik, mint az I.megoldásban. Felvesszük az

α

szöget és szerkesztünk egy

ϱ

sugarú, mindkét szárt érintő kört (2. ábra). Az egyik szögszáron az érintés: pontból kiindulva felmérjük ‐ a szög csúcspontjától távolodó irányban ‐ az

a

távolságot. Az így nyert pont lesz az említett tétel alapján a hozzáírt. kör érintési pontja. A beírt és hozzáírt kör egy közös belső érintője metszi ki az

α

szög száraiból a

B

és

C

csúcspontokat.
A megoldhatóság feltétele: a hozzáírt kör középpontját

O_{1}

-gyel és sugarát

ϱ_{1}

-gyel jelölve, feladatunk csak akkor oldható meg, ha

ϱ + ϱ_{1} ≦ O O_{1}

. De

\begin{matrix} ϱ_{1} = ϱ + a \end{matrix}

és így feltételünk

\begin{matrix} 2 ϱ + \frac{asin\frac{α}{2}}{cos \frac{α}{2}} ≦ \frac{a}{cos \frac{α}{2}}, \end{matrix}

amiből

ϱ ≦ \frac{a (1 - sin \frac{α}{2})}{cos \frac{α}{2}} = 2 r sin \frac{α}{2} (1 - sin \frac{α}{2})

, ami megegyezik az I. megoldásból nyert feltétellel