Kezdőlap


Cím:	Az 1952. évi Rákosi Mátyás matematikai verseny
Füzet:	1952/szeptember, 1 - 13. oldal	PDF \| MathML
Témakör(ök):	OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A Rákosi Mátyás matematikai tanulmányi verseny, mely ebben az évben került először kiírásra és pedig a középiskolák III. év IV. osztályú tanulói részére, mind a mennyiséget, mind a minőséget tekintve felülmúlja a tavaly nagy sikerű Arany Dániel versenyt. Az I. fordulóra ‐ mely ápr. 19-én az iskoláknál zajlott le ‐ 219 iskola összesen 3114 tanulót nevezett, de mivel a benevezett iskolákon kívül is indult néhány iskola a résztvevők száma kb. 3150-re tehető. A beadott dolgozatok száma 2921 volt.
Az I. fordulón a következő 3 feladatot kellett a versenyzőknek 4 órán belül megoldani:
1. Legyen adva két egymásra merőleges egyenes és egy pont. A pont körül rajzoljunk kört tetszésszerinti sugárral, de úgy, hogy mind a két egyenest messe. E metszéspontokban emeljünk merőlegest az egyenesekre és keressük meg ezek metszéspontjait. Milyen vonalat írnak le a metszéspontok, ha a kör sugarát változtatjuk?
2. Egy üzem az ötéves terv első évében $6 %$ -kal emeli évi termelését, a második évben pedig további $8 %$ -kal. A további három év alatt évente ugyanannyi százalékkal akarják emelni a termelést, úgyhogy a termelésnek a terv egész folyamán elért emelkedése átlagos évi $10 %$ -nak feleljen meg. Hány százalékkal kell emelni évente a termelést?
3. Egy egyenlő oldalélű négyzetes gúla alapéle $26$ cm, a szomszédos oldallapok $120^{\circ}$ -os szöget zárnak be egymással. Milyen magas a gúla?
Tekintettel arra, hogy a közgazdasági középiskolákban koordináta geometriát nem tanulnak, az 1. feladat pótlására még egy szabványos példa számtani haladványra is ki volt tűzve. A két feladat között a versenyzők választhattak.
A döntő II. forduló az első fordulóhon elért eredmény alapján kiválasztott 281 versenyző közt folyt le május 18-án d. e. 10 órától d. u. 3-ig, mégpedig Budapesten (168 induló), Szegeden (25 induló), Debrecenben (15 induló ‐ köztük egy II. osztályos versenyen kívül), Miskolcon (12 induló), Pécsett (15 induló), Veszprémben (16 induló), Győrött (17 induló) és Egerben (13 induló).
A döntőben a következő 3 feladat volt kitűzve:
1. Adva van a síkban $A$ és $B$ pont. Hol kell elhelyezni a síkban a $C$ pontot, hogy a $C A$ távolság $2, 6$ -szerese legyen a $C B$ távolságnak, és a $B A C$ szög lehető legnagyobb legyen?
2. Egy vasútvonalon $A$ helységből személyvonat indul $C$ helységbe. Amikor a vonat $B$ -n átfut, onnan egy tehervonat indul $A$ felé. Amidőn pedig a tehervonat $A$ -ba érkezik, egy gyorsvonat indul $A$ -ból $C$ felé, s ez éppen a $C$ állomáson éri utol a korábban említett személyvonatot. $A$ és $B$ közt félúton egy diák megfigyeli, hogy a személyvonat áthaladása után $15$ perc múlva futott át a tehervonat és újabb $11$ perc elteltével a gyorsvonat. $A$ -tól $B$ $10$ km-re van. Kérdés, hány km-re van $B$ -től a $C$ helység? (Feltesszük, hogy a vonatok egyenletes sebességgel haladnak.)
3. Bizonyítandó, hogy ha $a + b + c = 0$ , akkor

\begin{matrix} (\frac{a - b}{c} + \frac{b - c}{a} + \frac{c - a}{b}) (\frac{c}{a - b} + \frac{a}{b - c} + \frac{b}{c - a}) = 9 \end{matrix}

A versenyzők túlnyomó része legalább egy feladatot jól oldott meg. 74 versenyző volt, aki vagy legalább 2 feladatot lényegében megoldott, vagy egyre szellemes megoldást adott. Ezek közül kiemelkedett 15 dolgozat (eltekintve a versenyen kívül indult tanuló dolgozatától), melyek szerzői többé-kevésbé teljes megoldást adtak mindhárom feladatra, vagy 2 feladatnak adtak teljes megoldását, de valamelyik megoldásuk kiemelkedő. A minősítésre leginkább az első feladat adott módot. Ezt sokfelől próbálták megközelíteni a versenyzők, és különböző mértékben sikerült a megoldás lényegére rátapintaniuk.
A 15 dolgozat közül 3 találja meg a lényegre rámutató választ, ezek szerzői Kántor Sándor, Dömölki Bálint és Keresztély Sándor. Mindhárman megoldják a másik két feladatot is. Ezek közül is kiemelkedik Kántor Sándor dolgozata. Az első feladatnak két különböző módon adja megoldását és vázolja egy harmadik megoldási lehetőség menetét. A második feladatot egyenletekkel röviden, világosan megoldja, emellett ad egy egész elemi okoskodással történő megoldást is A harmadik feladatnak ügyes, világos megoldását adja. Fogalmazása rövid, tömör. Világosan emeli ki a lényeget.
Dömölki és Keresztély dolgozata egyféle megoldást ad, mindegyik feladatra s nem mindenütt találja meg a legrövidebb utat, bár eljutnak mindegyik feladatnak a teljes megoldásához.
Az első feladatra legegyszerűbb megoldást Fehér János ad, ő azonban nem oldja meg a harmadik feladatot. A második feladatra Ádám András egyszerű grafikus megoldást ad, nem oldja meg az első feladatot. A harmadik feladat megoldásában Szekerka Pálnak van egy ügyes ötlete, amellyel a megoldást áttekinthetővé teszi, viszont az első feladatnál nem sikerül sokszori próbálkozás ellenére az észrevett geometriai viszonyokat bizonyítania.
A K. M. a bírálóbizottság véleményének meghallgatása utána következő döntést hozta:

1 díj (oklevél és 1000 Ft pénzjutalom):
Kántor Sándor (Debrecen, Ref. Koll. g. III. o. t.).
2 díj (oklevél és 500 Ft pénzjutalom):
Dömölki Bálint (Bp. XI., Apáczai Csere János g. III. o. t.),
Keresztély János (Miskolc, Földes Ferenc g. III. o. t.).

I. dicséretben és nagyobb könyvjutalomban részesültek:

\begin{matrix} Ádám András & (Hajdúszoboszló, Irinyi János g. IV.) \\ Bársony András & (Nagykanizsa, Irányi Dániel g.) \\ Durst Endre & (Szolnok, Beloiannisz gimn. IV.) \\ Fehér János & (Győr, Révai g.) \\ Járfás László & (Budapest, X., Széchenyi g.) \\ Klopfer Ervin & (Bp. VIII., Kohó- és gépipari techn. IV.) \\ Nagy Tibor & (Vác, Sztáron Sándor gimn.) \\ Rédly Elemér & (Pannonhalmi g. III.) \\ Révész Pál & (Bp. VII., Madách g. IV.) \\ Szekerka Pál & (Bp. VI., Kölcsey g. IV.) \\ Villányi Ottó & (Bp. IV. Könyves Kálmán g. IV.) \\ Zalán János & (Győr, Révai g.) \end{matrix}

II. dicséretet és könyvjutalmat nyertek:

Adány László (Bp. X., I. László g.), Adorján László (Debrecen, Kohó- és gépipari techn. IV.), Balázs Béla (Bp. VII., Evang. g. III.), Bán István (Bp. V., Berzsenyi gimn. IV.), Bánkövi György (Bp. XI., József Attila g. III.), Beretvás Tamás (Bp. V., Berzsenyi g. III.), Billes Ferenc (Bp. XIV., 2. sz. vegyipari techn.), Csom Gyula (Sümeg, Korvin Ottó g. IV.), Deák Gedeon (Bp. V., 1. sz. textilipari techn. IV.), Dékány Sándor (Bp. XI., József Attila g. III.), Egri György (Bp. V., Eötvös gimn. IV.), Fellegi Iván (Bp. XIV., I. István g.), Földvári György (Bp. V., Eötvös g. IV.), Frajka Zoltán (Karcag, Gábor Áron g. III.), Gersits Ferenc (Bp. X., I. László g. III.), Gönczi Anikó (Bp. I., Szilágyi Erzsébet Ig. IV.), Ivits Iván (Bp. IX., Fáy g. IV.), Halmos Lajos (Bp. I., Fürst S. g. IV.), Harsányi Ibolya (Bp. XIX., Landler Jenő g.), Hartl Aladár (Eger, Dobó István g.), Kelen Rudolf (Bp. X., I. László g. IV.), Kerepesi Károly (Bp. XIV., 2. sz. vegyipari techn.), Kiss Gábor (Szeged, Radnóti g. IV.), Kiss Lajos (Debrecen, Csokonai g. III.), Kollár Mihály (Szarvas, Vajda Péter g. IV.), Kovács István (Bp. XI., József Attila g. IV.), Kövér György (Bp. IX., Ref. g. III.), Lakósi László (Keszthely, Vajda János g.), Malatinszki Jenő (Bp. XIV., Maxim Gorkij isk.), Martin Sándor (Szeged, Radnóti g. III.), Markó László (Bp. XVI., Corvin Mátyás g.), Mina János (Kiskunhalas, Sziládi Áron g. III.), Mitsányi Attila (Bp. XIV., Maxim Gorkij isk.), Molnár Lóránt (Bp. VIII., Fazekas g.), Nagy Ferenc (Szeged, Radnóti g. III.), Nagy Lajos (Aszód, Petőfi g.), Németh László (Gyula, Erkel Ferenc g. IV.), Neogrády Dezső (Keszthely, Vajda János g.), Oláh Tibor (Miskolc, Mikszáth g.), Pataki György (Bp. VII., Madách g. IV.), Rockenbauer Magda (Bp. X., I. László g. III.), Schwirg József (Bp. IX., 4. sz. Gépipari techn. III.), Serf Egyed (Bp. I., Fürst g. IV.), Spiró János (Bp. V., Berzsenyi g. IV.), Szakács Péter (Bp. VI., 1. sz. Élelmiszeripari techn.), Székely László (Cegléd, Kossuth g.), Szilárd Katalin (Bp. VI., Kossuth Zsuzsa g. III.) Szondy Tamás (Bp. III., Árpád g.), Telkes Zoltán (Aszód, Petőfi g. III.), Tölgyesi István (Nyíregyháza, Kossuth g. IV.), Turi István (Battonya, Mikes Kelemen g.), Varsányi Tamás (Bp. VIII., Fazekas g. III.), Zobor Ervin (Nagykanizsa, Irányi Dániel g. III.).

Alábbiakban adjuk a kitűzött feladatok megoldásait.

Az I. forduló feladatai

1. feladat.
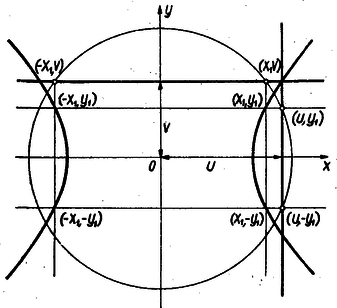
Megoldás: A körnek az egyenesekkel való metszéspontjai szimmetrikusak a pontból az egyenesekre bocsátott merőlegesekre nézve, tehát célszerű az utóbbi két egyenest koordináta-tengelynek választani, az adott pont lesz tehát az origó. Legyen a ,,függőleges'' egyenes távolsága az

Y

tengelytől

u

, a ,,vízszintesé'' az

X

-tengelytől

v

(

u

és

v

előjellel veendők). A kör sugara

r

nyilván nem legkisebb sem

| u |

sem

| v |

-nél. Az

r

sugarú kör által létesített

4

metszéspont:

(x_{1}, v),

(- x_{1}, v)

(u, y_{1})

(u, - y_{1})

és e metszéspontokban emelt merőlegesek metszéspontjainak koordinátái:

(x_{1}, y_{1})

(- x_{1}, y_{1})

(x_{1}, - y_{1})

(- x_{1}, - y_{1})

. Az előbbi

4

pont rajta van az origó körül húzott

r

sugarú körön, tehát koordinátái kielégítik a következő két egyenletet:

\begin{matrix} x_{1}^{2} + v^{2} = r^{2} \end{matrix}

(1)

és

\begin{matrix} u^{2} + y_{1}^{2} = r^{2} \end{matrix}

(2)

r

-et kiküszöböljük az által, hogy pl. (1)-ből kivonjuk (2)-t, az

\begin{matrix} x_{1}^{2} - y_{1}^{2} + v^{2} - u^{2} = 0, \end{matrix}

vagyis

\begin{matrix} x_{1}^{2} - y_{1}^{2} = u^{2} - v^{2} \end{matrix}

egyenletet kapjuk. Az indexet most már elhagyva annak hangsúlyozására, hogy ha

r

változik az

x_{1}

és

y_{1}

, értékek is változnak és feltéve, hogy

u^{2} \neq v^{2}

\begin{matrix} \frac{x^{2}}{u^{2} - v^{2}} - \frac{y^{2}}{u^{2} - v^{2}} = 0, \end{matrix}

| u | = | v |

; akkor az egyenlet így alakul:

\begin{matrix} x^{2} - y^{2} = (x - y) (x + y) = 0. \end{matrix}

Az előbbi egyenlő oldalú hiperbola egyenlete, melynek aszimptotái a koordináta-tengelyek szögfelező egyenesei, az utóbbi egyenletet viszont éppen e két szögfelező pontjainak koordinátái elégítik ki. A

r

változtatásával nyert

(x, y)

pontok mindig kielégítik az első, ill. a második egyenletet, a szerint, hogy milyen

u

és

v

értéke.
Fordítva, ha egy

(x_{0}, y_{0})

pontra nézve

x_{0}^{2} - y_{0}^{2} = u^{2} - v^{2}

(vagyis az

x_{0}

y_{0}

pont rajta van a fenti vonalon), akkor e pontból az adott egyenesekre bocsátott merőlegesek talppontjai:

(x_{0}, v)

és

(u, y_{0})

. Ezek távolsága az origótól:

\sqrt[]{x_{0}^{2} + v^{2}}

és

\sqrt[]{u^{2} + y_{0}^{2}}

a fenti egyenlőség szerint egyenlő, tehát e talppontok rajta vannak az origó körül rajzolt

\begin{matrix} r = \sqrt[]{x_{0}^{2} + v^{2}} = \sqrt[]{u^{2} + y_{0}^{2}} \end{matrix}

sugarú körön, vagyis az

(x_{0}, y_{0})

pont kielégíti a mértani hely feltételeit.
Ezek szerint, ha

| u | \neq | v |

, akkor a mértani hely egyenlő oldalú hiperbola, melynek középpontja az adott pont, tengelyei párhuzamosak az adott egyenesekkel, a tengelyek hosszának fele

\sqrt[]{u^{2} - v^{2}}

. A hiperbola átmegy az adott egyenesek

(u, v)

metszéspontján.
Ha

| u | = | v |

vagyis az adott pont speciálisan a két adott egyenes egyik szögfelezőjén van, akkor a mértani hely a kérdéses szögfelezőből és az adott ponton át rá merőlegesen húzott egyenesből áll. Azt szoktuk mondani, hogy a hiperbola ebben az esetben két egyenesre fajul.

Megjegyzés: Ha az adott egyeneseket választjuk a koordinátarendszer tengelyeinek és az adott pont:

O (u, v)

akkor a geometriai hely egyenlete:

\begin{matrix} \frac{{(x - u)}^{2}}{u^{2} - v^{2}} - \frac{{(y - v)}^{2}}{u^{2} - v^{2}} = 1 \end{matrix}

alakú lesz.

2. feladat.
Megoldás: Legyen a terv előtti év termelése

T

, akkor az első tervévben a termelés

T_{1} = T + \frac{6}{100} T = T \cdot 1, 06

volt. A második tervévben a

T_{1}

növekedett

8 %

-kal, vagyis a termelés a 2. tervévben

T_{2} = T_{1} \cdot 1, 08 = T \cdot 1, 06 \cdot 1, 08

. Ezt a

T_{2}

termelést akarják emelni

3

éven át, évente állandó

x %

-kal úgy, hogy az utolsó tervévben a termelés

T_{5} = T_{2} {(1 + \frac{x}{100})}^{3}

egyenlő legyen

T \cdot 1, 1^{5}

-nel.
Ha az egyszerűség kedvéért

1 + \frac{x}{100}

helyett

q

-t írunk, akkor

T_{2} q^{3} = T \cdot 1, 06 \cdot 1, 08 \cdot q^{3} = T \cdot 1, 1^{5}

,
amiből

\begin{matrix} q^{3} = \frac{1, 1^{5}}{1, 06 \cdot 1, 08}, \end{matrix}

vagyis

\begin{matrix} q = \sqrt[3]{\frac{1, 1^{5}}{1, 06 \cdot 1, 08}} = 1, 121 \end{matrix}

és így

\begin{matrix} x = 100 (q - 1) = 12, 1 % . \end{matrix}

Tehát a hátralevő

3

évben a termelést évente

12, 1 %

-kal kell emelni.

Megjegyzés: A szöveg úgy is értelmezhető, hogy az ötödik év termelése helyett, az öt évi össztermelésről van szó. Ez esetben (a

T

-vel való egyszerűsítés után, az

\begin{matrix} 1, 06 + 1, 06 \cdot 1, 08 (1 + q + q^{2} + q^{3}) = 1, 1 \frac{1, 1^{5} - 1}{0, 1} = 6, 71561 \end{matrix}

egyenlethez jutunk, amiből

\begin{matrix} q^{3} + q^{2} + q + 1 = \frac{6, 71561 - 1, 06}{1, 1448} = 4, 94 \end{matrix}

A jobboldali törtet

2

tizedes pontossággal kerekítettük, tekintve, hogy az egyenletet grafikusan fogjuk megoldani, és ebből nagyobb pontosságra aligha számíthattunk.
Ha mindkét oldalt

(q - 1)

-gyel szorozzuk, akkor

\begin{matrix} q^{4} - 1 = 4, 94 q - 4, 94, \end{matrix}

vagyis

\begin{matrix} q^{4} = 4, 94 q - 3, 94. \end{matrix}

(q - 1)

-gyel való szorzás folytán ennek a

4

-edfokú egyenletnek ‐ mely grafikusan könnyen megoldható ‐ egyik gyöke

1

, a többi gyökei megegyeznek az eredeti harmadfokú egyenlet gyökeivel.
A grafikus megoldás szempontjából célszerű egyenletünk mindkét oldalát

10

-zel osztani:

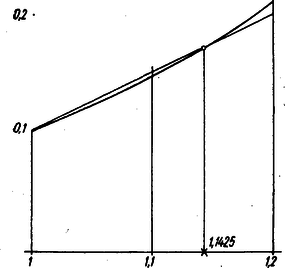
\begin{matrix} 0, 1 q^{4} = 0, 494 q - 0, 394. \end{matrix}

Ábrázoljuk az

y_{1} = 0, 1 q^{4}

és

y_{2} = 0, 494 q - 0, 394

függvényeket:

\begin{matrix} \begin{matrix} q & 1 & 1, 1 & 1, 2 \\ y_{1} & 0, 1 & 0, 146 & 0, 208 \\ x_{2} & 0, 1 & 0, 149 & 0, 198 \end{matrix} \end{matrix}

Az ábrából leolvasható, hogy az egyenes a negyedrendű görbét a

q = 1

ponton kívül, még kb. a

q = 1, 1425

helyen metszi. (Könnyen meggyőződhetünk

4

-jegyű függvénytábla segítségével, hogy

q = 1, 141

-nél a negyedfokú függvény még az egyenes alatt van,

1, 144

-nél már biztosan felette van, tehát

1, 141 < q < 1, 144

.)
Tehát ez esetben az utolsó tervévben

14, 25 %

-kal kell évente emelni a termelést.

3. feladat.
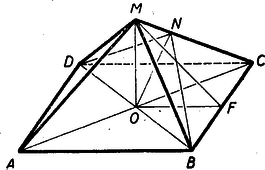
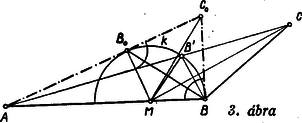
I. megoldás: A betűzést az ábra mutatja.

Legyen az alapnégyzet egy oldala

B C = a

, az alapnégyzet félátlója

O B = O C = \frac{a \sqrt[]{2}}{2}

. A keresett

O M

-et jelöljük

m

-mel. A

B D

átlón át az

M C

oldalélre merőleges sík messe az oldalélt

N

-ben. Tehát

O N ⊥ M C

.
A feltétel szerint a

B N D ∢ = 120^{\circ}

. Legyen

O C N ∢ = α

. Mivel a

B N D

egyenlőszárú háromszögben a szárakkal szembenfekvő szögek

30^{\circ}

-osak, azért

\begin{matrix} sin α = \frac{O N}{O C} = \frac{O N}{O B} = tg O B N ∢ = tg 30^{\circ} = \frac{1}{\sqrt[]{3}} . \end{matrix}

Ezt felhasználva, az

O C M

derékszögű háromszögből

\begin{matrix} m = O C \cdot tg α = O C \cdot \frac{sin α}{\sqrt[]{1 - sin^{2} α}} = \frac{a \sqrt[]{2}}{2} \cdot \frac{1 / \sqrt[]{3}}{\sqrt[]{1 - 1 / 3}} = \frac{a \sqrt[]{2}}{2 \sqrt[]{2}} = \frac{a}{2} . \end{matrix}

Jelen esetben

a = 26

cm és így

m = 13

cm.
A keletkező számos derékszögű háromszög sokféle lehetőséget ad arra is a versenyzők ezeket ki is aknázták ‐ hogy trigonometria felhasználása nélkül számítsuk ki a magasságot. Egy ilyen pl. a következő.

II. megoldás:

B F = O F = \frac{a}{2}

. A

B O N ▵

-ből

B N = \frac{B O}{sin 60^{\circ}} = \frac{a \sqrt[]{2}}{2} / \frac{\sqrt[]{3}}{2} = \frac{a \sqrt[]{2}}{\sqrt[]{3}} = \frac{a \sqrt[]{6}}{3} .

M F C

és a

B N C

derékszögű háromszögek hasonlók, mert a

C

-nél fekvő hegyes szögük közös, tehát

\begin{matrix} \frac{M F}{M C} = \frac{B N}{a} = \frac{\sqrt[]{6}}{3}, \end{matrix}

vagyis

\begin{matrix} \frac{M F^{2}}{M C^{2}} = \frac{m^{2} + \frac{a^{2}}{4}}{m^{2} + \frac{a^{2}}{2}} = \frac{2}{3}, \end{matrix}

amiből

\begin{matrix} 3 m^{2} + \frac{3 a^{2}}{4} = 2 m^{2} + a^{2}, \\ m^{2} = \frac{a^{2}}{4}, és így m = \frac{a}{2} . \end{matrix}

III. megoldás: Legyen

M C = b

és

B N = p

. Mivel a feladat szerint

B N O ∢ = 60^{\circ}

, azért

O N = \frac{p}{2}

.
A

C O M ▵

kétszeres területe kétféleképpen állítható elő:

\begin{matrix} 2 t = b \cdot \frac{p}{2} = \frac{a}{2} \sqrt[]{2} \cdot m, \\ vagyis b p = a m \sqrt[]{2} . & (1) \end{matrix}

B C M ▵

kétszeres területe hasonlóképpen

\begin{matrix} b p = a \sqrt[]{m^{2} + \frac{a^{2}}{4}} . \end{matrix}

(1) és (2)-ből következik, hogy

\begin{matrix} a m \sqrt[]{2} = a \sqrt[]{m^{2} + \frac{a^{2}}{4}}, \\ 2 m^{2} = m^{2} + \frac{a^{2}}{4}, \end{matrix}

amiből

\begin{matrix} m = \sqrt[]{\frac{a^{2}}{4}} = \frac{a}{2} . \end{matrix}

IV. megoldás: Vegyünk

6

, a feltételeknek megfelelő, gúlát és helyezzünk először hármat egymás mellé úgy, hogy csúcsaik és egy oldalélük egybeessenek. Mivel az oldallapok szöge

120^{\circ}

és

3

ilyen lapszög került egymás mellé, a

3

gúla hézag nélkül összeillik. Két-két gúla szomszédos oldallapjai pedig

360^{\circ} - 2 \cdot 120^{\circ} = 120^{\circ}

-os szöget fognak alkotni. Így a szomszédos gúlák közé egy-egy újabb gúlát illesztve úgy, hogy ezek csúcsa is összeessék a már összeillesztett gúlák közös csúcsával, zárt testet kapunk, melyet

6

négyzet (a

6

gúla alaplapja) határol. Ez a test tehát csak kocka lehet. Két csúccsal szembefordított gúla magasságainak összege egyenlő a kocka élével, vagyis a gúla alapélével. Ebből következik, hogy a gúla magassága az alapél hosszának felével egyenlő.

Így oldotta meg a feladatot Szabó László (Aszód, Petőfi g. IV. o. t.) és Tuska Ferenc (Cegléd, Kossuth g. IV. o. t.)
A pályázók legnagyobb része trigonometriai táblákkal szögeket határozott meg, ami ‐ mint a fenti megoldások matatják ‐ teljesen felesleges.

A II. forduló feladatai

I. feladat.
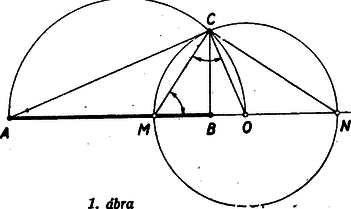
I. megoldás: A

C

pont rajta van azon az Apollonius-féle körön, melynek minden

P

pontjára nézve

\frac{P B}{P A} = \frac{1}{2, 6} = \frac{5}{13}

. A

B A C ∢

akkor maximális, ha

A P

a kör érintője. Ez az érintési pont lesz tehát a keresett

C

pont. Kimutatjuk, hogy

C B A ∢

derékszög.

Az Apollonius-féle kör középpontját

O

-val és az

A B

egyenessel való metszéspontjait

M

és

N

-nel jelölve (1. ábra), a

C M

egyenes az

A B C_{▵}

A B

oldalát

\frac{M B}{M A} = \frac{5}{13} = \frac{C B}{C A}

arányban metszi, mert

M

is a kör egy pontja. Ebből viszont következik, bogy

C M

A C B ∢

felezője,

\begin{matrix} A C M ∢ + M C O ∢ = 90^{\circ}, \end{matrix}

(1)

mert az érintő merőleges a körsugárra.
Láttuk, hogy

A C M ∢ = M C B ∢

. Másrészt a

C O M

egyenlőszárú háromszögből

\begin{matrix} M C O ∢ = O M C ∢ . \end{matrix}

Helyettesítsük az (1) alatti egyenlőségben szereplő szögeket a velük egyenlő szögekkel

\begin{matrix} M C B ∢ + O M C ∢ = 90^{\circ}, \end{matrix}

de akkor az

M B C ▵

harmadik szöge,

M B C ∢

90^{\circ}

, vagyis az

A B C ▵

derékszögű és így

A B = \sqrt[]{A C^{2} - B C^{2}} = B C \sqrt[]{2, 6^{2} - 1} = B C \sqrt[]{5, 76} = 2, 4 B C

, vagyis

\begin{matrix} B C = \frac{5}{12} A B . \end{matrix}

Tehát a

C

pontot a

B

pontban

A B

-re emelt merőleges egyenesen kell elhelyezni

B

-től

\frac{5}{12} \cdot A B

távolságban.

II. megoldás: Képzeljük a feladatot megoldottnak és alkalmazzuk az

A B C ▵

-re a sinus-tételt;

\begin{matrix} \frac{sin α}{sin β} = \frac{C B}{C A} = \frac{5}{13} \end{matrix}

amiből

\begin{matrix} sin α = \frac{5}{13} \cdot sin β . \end{matrix}

Mivel

α

szükségképpen hegyesszög, azért

α

akkor maximális, ha

sin α

maximális;

sin α

pedig akkor veszi fel a legnagyobb értéket, ha

sin β = 1

, vagyis

β = 90^{\circ}

III. megoldás: Tekintsünk egy

C_{1}

pontot, melyre nézve

\frac{C_{1} B}{C_{1} A} = \frac{1}{2, 6} = \frac{5}{13}

és

C_{1} B A ∢

hegyes, továbbá egy

C_{2}

pontot, melyre nézve

\frac{C_{2} A}{C_{2} B}

értéke ugyancsak

\frac{5}{13}

, de a

C_{2} B A ∢

tompa. Legyen

C_{1} C'_{1}

ill.

C_{2} C'_{2}

, a

C_{1}

ill.

C_{2}

pontoknak távolsága az

A B

egyenestől (2. ábra) és az

A

-nál keletkező szögeket jelöljük

α_{1}

ill.

α_{2}

-vel.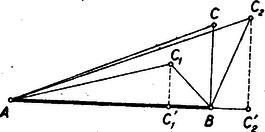

2. ábra

Mivel

C_{1} C'_{1} < C_{1} B

és

C_{2} C'_{2} < C_{2} B

, azért

\begin{matrix} sin α_{1} = \frac{C C_{1}}{C_{1} A} < \frac{C_{1} B}{C_{1} A} = \frac{5}{13} és sin α_{2} = \frac{C_{2} C'_{2}}{C_{2} B} < \frac{C_{2} B}{C_{2} A} = \frac{5}{13} . \end{matrix}

Tehát az

A

-nál levő szög sinusa mindig kisebb

\frac{5}{13}

-nál, kivéve, ha a

C B A ∢

derékszög, ekkor

sin α = \frac{C B}{C A} = \frac{5}{13}

, vagyis ez esetben

sin α

és vele együtt

α

maximális.
Így oldotta meg a feladatot Fehér János (Győr, Révai gimn.)

IV. megoldás: Mindazon közös

A B

oldalú

A B C

háromszögekben, melyekre teljesül az

A C : B C = 2, 6

kikötés, a

C

-nél fekvő szög felezője az

A B

oldalt olyan

M

pontban metszi, melyre

A M : B M = A C : B C = 2, 6

. Az

M

pont helyzete független a háromszög alakjától. Tükrözzük a

C M B

háromszöget a

C M

szögfelezőre. A

B

pont tükörképe

B'

A C

háromszögoldalra esik és

\begin{matrix} M B' = M B \end{matrix}

C

pont helyzetétől független távolság. Az összes ilyen pontok tehát az

M

középpontú és

B

-n átmenő

k

körön sorakoznak. (3. ábra).

Megfordítva, ha

B'

ennek a körnek tetszés szerinti pontja, akkor messük el az

A B'

egyenest a

B M B' ∢

felezőjével. Az így keletkező

A B C

háromszögben

M C

szögfelező, mert

M B'

tükörképe

M C

-re

M B

, a

C

ponté pedig önmaga, tehát a

C B'

oldalegyenes tükörképe

C B

. Ebből következik az is, hogy

\begin{matrix} A C : B C = A M : B M = 2, 6, \end{matrix}

tehát az

A B C ▵

megfelel a követelményeknek.
Az eredeti feladat tehát helyettesíthető azzal, hogy a

k

kör mely

B_{0}

-ját kell

A

-val összekötni, hogy a keletkező

B_{0} A B ∢

a lehető legnagyobb legyen. Ez a

B_{0}

nyilván az

A

-ból húzható érintő érintési pontja. Ez esetben

\begin{matrix} M B_{0} ⊥ A B_{0} \end{matrix}

Szerkesszük meg a fent leírt módon az ezen

B_{0}

ponthoz tartozó

A B C_{0}

háromszöget. Ebben is

M B C_{0} ▵

M B_{0} C_{0} ▵

tükörképe, s így

\begin{matrix} A B C_{0} ∢ = M B_{0} C_{0} ∢ = 90^{\circ} . \end{matrix}

V. megoldás: Keressük azon közös

A B

oldalú

A B C

háromszögek közül, melyekre

A C : B C = 2, 6

azt, amelyben a

B A C ∢

a lehető legnagyobb. A szögek azonban nem változnak, ha a háromszögeket nagyítjuk, vagy kicsinyítjük. Így helyettesíthetjük az összes háromszöget olyanokkal, melyekben az

A C

oldal közös. Ekkor

\begin{matrix} B C = \frac{A C}{2, 6} = \frac{5}{13} A C \end{matrix}

is az összes háromszögekben egyenlő, az összes

B

pontok tehát egy

C

körül

r = \frac{5}{13} \cdot A C

sugárral rajzolt körön vannak. A

B A C ∢

akkor maximális, ha

A B

e kör érintője, tehát

B C ⊥ A B

és Pythagoras-tétele alapján

\begin{matrix} A B = 2, 4 B C, vagyis B C = \frac{5}{12} \cdot A B . \end{matrix}

Számosan differenciálással oldották meg a feladatot, ami ‐ mint láttuk ‐ teljesen felesleges.

2. feladat.
I. megoldás: Jelöljük a keresett

B C

távolságot

x

-szel és legyen a személy-, teher- és gyorsvonat sebessége rendre

c_{1}

c_{2}

, ill.

c_{3}

km/perc. A diák megfigyelése szerint

\begin{matrix} \frac{5}{c_{1}} + \frac{5}{c_{2}} = 15, & (1) \\ \frac{5}{c_{2}} + \frac{5}{c_{3}} = 11. & (2) \end{matrix}

B C = x

távolságot a személyvonat

\frac{x}{c_{1}}

perc alatt teszi meg és ez alatt a tehervonat

\frac{10}{c_{2}}

percig van úton

B

-től

A

-ig, és utána a gyors

\frac{10 + x}{c_{3}}

percig

A

-tól

C

-ig, tehát

\begin{matrix} \frac{x}{c_{1}} = \frac{10}{c_{2}} + \frac{10 + x}{c_{3}} . \end{matrix}

(3)

Tehát

3

egyenletünk van

4

ismeretlennel, vagyis nem határozhatók meg mind az ismeretlenek, de jelen esetben

x

meghatározható, csak

c_{1}

c_{2}

és

c_{3}

marad határozatlan.
(1)-ből (2)-t kivonva

\begin{matrix} \frac{5}{c_{1}} - \frac{5}{c_{3}} = 4, amiből \frac{1}{c_{1}} - \frac{1}{c_{3}} = \frac{4}{5} . \end{matrix}

(4)

(2)-ből

\begin{matrix} \frac{1}{c_{2}} + \frac{1}{c_{3}} = \frac{11}{5}, \end{matrix}

(5)

(3)-ból

\begin{matrix} \frac{x}{c_{1}} - \frac{x}{c_{3}} = \frac{10}{c_{2}} + \frac{10}{c_{3}}, \end{matrix}

vagyis

\begin{matrix} x (\frac{1}{c_{1}} - \frac{1}{c_{3}}) = 10 (\frac{1}{c_{2}} + \frac{1}{c_{3}}) . \end{matrix}

(4) és (5) figyelembevételével

\begin{matrix} \frac{4}{5} x = 10 \cdot \frac{11}{5}, \end{matrix}

amiből

\begin{matrix} x = \frac{110}{4} = 27, 5 km. \end{matrix}

II. megoldás: A diák megfigyelése szerint a személyvonat és a tehervonat egymásután 5 ‐ 5 km-t tesz meg összesen

15

perc alatt, míg a tehervonat és gyorsvonat ugyancsak 5 ‐ 5 km-t tesz meg egymásután összesen

11

perc alatt. Ebből következik, hogy a gyorsvonat 5 km-t 4 perccel rövidebb idő alatt tesz meg mint a személyvonat. A gyorsvonat az

A B

távolság

F

felező pontján

15 + 11 = 26

perccel a személyvonat után halad át. Mivel 5 km-ként hoz be 4 perc időhátrányt, azért 26 perc időhátrányt

6, 5 \cdot 5 km = 32, 5 km

után hoz be. Tehát

F C = 32, 5

km és így

B C = F C - F B = 32, 5 - 5 = 27, 5

km.

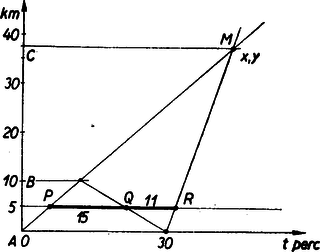
III. megoldás: Ábrázoljuk grafikusan a vonatok menetét. Először tüntessük fel az

A

pontból

0

perckor kiinduló személyvonat megtett km-eit, mint a

t

percek függvényét, tetszőleges sebesség mellett vagyis az

A P

egyenest tetszőleges szög alatt húzhatjuk (l. ábrát).

10

km megtevése után

B

-ből indul vissza a tehervonat

A

-ba ismét (bizonyos mértékig) tetszőleges sebességgel. A tehervonat

15

percel a személyvonat után ér az

5

km-hez, tehát ábránkon

P Q = 15

perc, amiből következik, hogy a tehervonat

A

-ba

30

perccel a személynek (

0

perckor történt) indulása után érkezik. (Ábránkról geometriailag leolvasható. Mivel a gyorsvonat sebességének pozitívnak és felülről korlátosnak kell lennie, azért a tehervonat sebessége sem egészen tetszőleges. Ha a gyorsvonat részére óránkénti

150

km-es sebességet veszünk felső határnak, akkor

5

km megtevésére a gyorsnak legalább

2

percre, a személynek pedig legalább

2 + 4 = 6

percre van szüksége, tehát az

5 P

távolság

≧ 6

perc. Ebből következik, hogy

P Q = 15

perc távolság legfeljebb az

5 P

távolság

2, 5

-szerese.)
A gyorsvonat a

30

-ik percben indul el, de ennek sebessége már meg van határozva az előbbi két tetszőlegesen felvett sebesség által, mert

11

perccel a tehervonat után kell az

5

km-hez érnie. Tehát

Q R = 11

perc, vagyis az

R

pont meg van határozva és így a gyorsvonat menetét feltüntető egyenes is meg van határozva. Ez utóbbinak a személyvonat menetét feltüntető egyenessel való metszéspontja

M (x, y)

M

-nek

y

ordinátája, mely km-eket jelent, ábránkról leolvasható, de könnyen pontosan ki is számítható ábránkból

\begin{matrix} y : (y - 5) = M A : M P = 30 : 26, \end{matrix}

miből

\begin{matrix} 26 y = 30 y - 150, \end{matrix}

\begin{matrix} y = 37, 5 és így B C = y - 10 = 27, 5 km. \end{matrix}

Lényegében így oldotta meg a feladatot Ádám András (Hajdúszoboszló, Irinyi János g. IV. o. t.).

3. feladat.
I. megoldás: Bebizonyítandó tételünk így is írható:

\begin{matrix} 3 + \frac{c}{a - b} (\frac{b - c}{a} + \frac{c - a}{b}) + \frac{a}{b - c} (\frac{a - b}{c} + \frac{c - a}{b}) + \\ + \frac{b}{c - a} (\frac{a - b}{c} + \frac{b - c}{a}) = 9, \end{matrix}

vagyis

\begin{matrix} \frac{c}{a - b} \cdot \frac{b^{2} - b c + a c - a^{2}}{a b} + \frac{a}{b - c} \cdot \frac{a b - b^{2} + c^{2} - a c}{b c} + \\ + \frac{b}{c - a} \cdot \frac{a^{2} - a b + b c - c^{2}}{a c} = \frac{c}{a - b} \cdot \frac{- (a + b) (a - b) + c (a - b)}{a b} + \\ + \frac{a}{b - c} \cdot \frac{- (b + c) (b - c) + a (b - c)}{b c} + \frac{b}{c - a} \cdot \frac{- (c + a) (c - a) + b (c - a)}{a c} = \\ = \frac{c [- (a + b) + c]}{a b} + \frac{a [- (b + c) + a]}{b c} + \frac{b [- (c + a) + b]}{a c} = 6 \end{matrix}

Mivel a feltétel szerint

- (a + b) = c

- (b + c) = a

és

- (c + a) = b

, azért

\begin{matrix} \frac{2 c^{2}}{a b} + \frac{2 a^{2}}{b c} + \frac{2 b^{2}}{a c} = 2 \cdot \frac{a^{3} + b^{3} + c^{3}}{a b c} = 6, \end{matrix}

vagyis

\begin{matrix} \frac{a^{3} + b^{3} + c^{3}}{a b c} = 3. \end{matrix}

(1)

Ennek helyességét kell tehát bizonyítanunk. Feltételünk szerint

c = - (a + b)

, és így

\begin{matrix} \frac{a^{3} + b^{3} + c^{3}}{a b c} = - \frac{a^{3} + b^{3} - {(a + b)}^{3}}{a b (a + b)} = - \frac{a^{3} + b^{3} - a^{3} - 3 a^{2} b - 3 a b^{2} - b^{3}}{a b (a + b)} = \\ \frac{3 a b (a + b)}{a b (a + b)} = 3. \end{matrix}

Ezzel tételünket bebizonyítottuk.

Jegyzet: Az adott feltételek mellett az (1) alatti azonosság még így is bizonyítható:

\begin{matrix} {(a + b + c)}^{3} = a^{3} + 3 a^{2} b + 3 a b^{2} + b^{3} + 3 {(a + b)}^{2} c + 3 (a + b) c^{2} + c^{3} = \\ = a^{3} & + b^{3} + c^{3} + 3 a b (a + b) + 3 {(a + b)}^{2} c + 3 (a + b) c^{2} = 0, és mivel a + b = \\ = - c, & azért \end{matrix}

\begin{matrix} a^{3} + b^{3} + c^{3} - 3 a b c + 3 c^{3} - 3 c^{2} = 0, \end{matrix}

amiből

\begin{matrix} a^{3} + b^{3} + c^{3} = 3 a b c . \end{matrix}

II. megoldás: Az

a

b

c

, számok mind különbözők és egyike sem lehet

0

, mert különben az adott szorzat értelmetlen.
Jelöljük a szorzat első tényezőjét

A

-val, második tényezőjét

B

-vel.

\begin{matrix} A = \frac{(a - b) a b + (b - c) b c + (c - a) a c}{a b c} = \\ = \frac{a^{2} b - a b^{2} + b^{2} c - b c^{2} + a c^{2} - a^{2} c}{a b c} = \frac{a^{2} (b - c) - a (b^{2} - c^{2} + b c (b - c)}{a b c} = \\ \frac{(b - c) [a^{2} - a (b + c) + b c]}{a b c} = \frac{(b - c) (a - b) (a - c)}{a b c} = - \frac{(a - b) (b - c) (c - a)}{a b c} . \end{matrix}

\begin{matrix} B = \frac{c (b - c) (c - a) + a (a - b) (c - a) + b (a - b) (b - c)}{(a - b) (b - c) (c - a)} = \\ = - \frac{a^{3} + b^{3} + c^{3} - a^{2} b - a b^{2} - a^{2} c - a c^{2} - b^{2} c - b c^{2} + 3 a b c}{(a - b) (b - c) (c - a)} \end{matrix}

Tehát

\begin{matrix} A B = \frac{a^{3} + b^{3} + c^{3} - a^{2} b - a b^{2} - a^{2} c - a c^{2} - b^{2} c - b c^{2} + 3 a b c}{a b c} . \end{matrix}

Adjuk hozzá a számlálóhoz az

{(a + b + c)}^{3} = a^{3} + b^{3} + c^{3} + 3 a^{3} b + 3 a b^{2} + 3 a^{2} c + 3 a c^{2} + 3 b^{2} c + 3 b c^{2} + 6 a b c

kifejezést, amely a feltételünk szerint

0

-val egyenlő.

\begin{matrix} A B = \frac{2 (a^{3} + b^{3} + c^{3} + a^{2} b + a b^{2} + a^{2} c + a c^{2} + b^{2} c + b c^{2}) + 9 a b c}{a b c} = \\ = \frac{2 [a^{2} (a + b + c) + b^{2} (a + b + c) + c^{2} (a + b + c)] + 9 a b c}{a b c} \end{matrix}

Mivel tétetelünk szerint a számláló első tagja

0

, azért

\begin{matrix} A B = \frac{9 a b c}{a b c} = 9, ami bizonyítandó volt. \end{matrix}

Így végezte el a bizonyítást Szekerka Pál (Bp. VI. Kölcsey g. IV. o. t.)
Sok pályázó hivatkozott arra, hogy egy azám és reciprokának összege

≧ 2

, megfeledkezve arról, hogy ez csak pozitív számokra érvényes.