Cím: Bolyai János (1952. november)
Szerző(k):  Kárteszi Ferenc 
Füzet: 1952/november, 65 - 75. oldal  PDF  |  MathML 
Témakör(ök): Egyéb írások

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

BOLYAI JÁNOS

 

    ≫ ... most többet nem szollhatok tsak  annyit: hogy  semmiből egy ujj más vi -lágot teremtettem...≪ (Temesvár, 1823.  nov. 3.)  

 
1802 december 15-én született Kolozsvárt a magyar tudomány legnagyobb büszkesége, a minden idők egyik legnagyobb matematikusa, Bolyai János. A Magyar Tudományos Akadémia decemberben Bolyai‐hetet rendez, hogy méltó ünneplésben juttassa kifejezésre a magyar tudomány megemlékezését.
Az anyagi világ terének megismerésében Euklides műve, az Elemek, két évezreden át uralkodó hatással irányította a kutatásokat. Bolyai János műve az Appendix pedig a tudomány fejlődésében forradalmi átalakulást robbantott ki és a modern térfogalom kialakulásában, száguldó fejlődésében gazdag forrásnak bizonyult. A matematika egyik legnagyobb, két évezreden át vajúdó problémáját tisztázta, s kaput nyitott a tudomány újabb, csodálatos fejlődése számára. Ma már egy évszázad matematikai alkotásaiban láthatjuk Bolyai eszméinek tükröződését és széles területen felismerhető hatását. Bolyai János nagyságát nemcsak az Appendix ‐ ez a híres matematikai remekmű ‐ hirdeti, hanem annak a matematika fejlődésére gyakorolt mélyre ható és széles körű hatása is.
Miben áll Bolyai János korszakalkotó felfedezése, mi volt az a két évezreden át minden kutatónak makacsul ellenálló nagy probléma, amelyet megoldott? Ennek a megértése komoly matematikai felkészültséget és érettséget követel. Mégis igyekszünk, a lehetőséghez képest, megvilágítani.
Egy felfedezés jelentőségének helyes értékeléséhez erősen hozzátartozik a probléma keletkezése, fejlődése és megoldása történetének ismerete. A szóbanforgó probléma története tudatosítja azt a tételt, hogy a tudomány társadalmi termék.
A geometriát tudománnyá az athéni matematikusok fejlesztették.1 Első ismereteiket az egyiptomiaktól és a babiloniaktól tanulták. Első ismereteik empirikusan megismert tételek voltak. Hasznát látták iparuk fejlesztésében, s kultúrájuk gyarapításában. Athénben a gyorsan fejlődő termelési rendszer a társadalmi viszonyok rohamos fejlődésére vezetett, s kialakult az a légkör, mely a tudomány fejlődését lehetővé tette. Először az empirikus ismeretek terén mutatkozott rohamos gyarapodás.
Az ilyen ismeretekkel való beható foglalkozás rávezette az athéni matematikusokat arra a felismerésre, hogy a geometriai megismerés számára a tapasztalat elvont általánosítása még nem nyújt kellő biztonságot. A geometriai ismeretek forrása a szemlélet (tapasztalat), azonban a puszta szemlélet még nem szülhet biztos ismeretet.
Rájöttek a szemlélet kritikai ellenőrzésének, a bizonyításnak a szükségességére és ezzel megteremtették az exakt tudomány módszerét.
Euklides művében ‐ az Elemek-ben ‐ érte el ez a fejlődés a csúcspontját. Miben áll Euklides nevezetes programja? A szemlélet szerepének szigorú korlátozásában.
Miért kell a szemlélet szerepét korlátoznunk? Hiszen a szemlélet a kutatásban az intuíció forrása. Igaz. Azonban a szemlélet szubjektív elemek szövevénye, s a legegyszerűbb szemléletes tartalmaktól eltekintve, bizonytalanságok, könnyelmű általánosítások, tévedések sugalmazója. Szükséges, hogy a bonyolultabb szemléletes összefüggéseket a legegyszerűbb szemléletes tartalmak viszonyára bontsuk. Ez az elemzés, kritikai ellenőrzés vezethet csak biztos ismeretekre.1
A szemlélet megbízhatatlanságára nézve tanulságos példa a következő. Tekintsük az 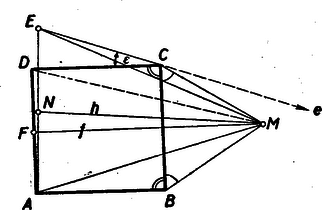ABCD négyzetet. Fordítsuk elegy igen kicsiny ε szöggel C pont körül a CD oldalt a CE állásba. (Az e a CE meghosszabbítása.) AD és AE felezőpontja F és N, felezőmerőlegese az f és h. Ezek metszéspontja az M.
 
 
1. ábra
 

Az AD felezőmerőlegesének M pontjára nyilván AM=DM érvényes. Az AE felezőmerőlegese is tartalmazza M-et, tehát AM=EM. E kettőből pedig DM=EM. Az AD és BC felező merőlegese közös, az f egyenes, tehát BM=CM. A négyzetből pedig AB=CD=CE. Tehát az ABM és ECM háromszögek oldalai páronként megegyező nagyságúak és így e két háromszög egybevágó. (1. ábra)
No de akkor a megfelelő szögeik egyenlők. Így ABM∢=ECM∢. Ez pedig képtelenség, hiszen az ábrából közvetlenül látható, hogy az utóbbi szög éppen az E nagyságú elforgatási szöggel nagyobb az előbbinél. Hol van a hiba gyökere?
Ott van a hiba elásva, hogy elfogadtuk a szemléletből azt a hibás állítást, hogy az M pont az e egyenesnek a négyzet felé eső partján van. Ha a túlsó partján volna, nem lehetne az ábrából leszűrt képtelenségre következtetni. Az a kérdés föltétlenül szigorú elemzésre szorul, hogy az M pont az e egyeneshez képest hol helyezkedik el.
Tekintsük csak az 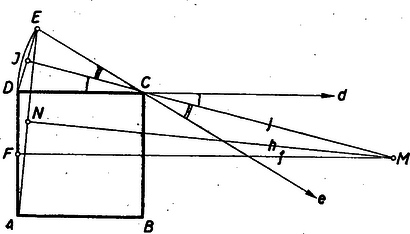ADE háromszöget. Ennek f és h két oldalfelező merőlegese. Ezek közös M pontja a háromszög köré írt kör középpontja. Az M-et a harmadik ‐ DE ‐ oldal felező merőlegesének, a j egyenesnek is tartalmaznia kell. Ha f egyenest DEC egyenlő szárú háromszögben tekintjük, nyilvánvaló, hogy az (ed)∢ felező egyenese. Ebből világos, hogy j az f-et az e-nek f-fel való metszéspontjától jobbra metszi, az az valóban a túlsó parton. (2. ábra)
 
 
2. ábra
 

E példa esetében a tapasztalat lazaságából eredő rejtett hiba feltárására törekedtünk. Az segített, hogy az egész okoskodást, minden tapasztalati mozzanatát, kétségtelenül biztos ismeretelemekkel egybevetve ellenőriztük. Bebizonyítottuk állításaink helyességét, cáfoltuk a hamis állításokat.
Euklides éppen a szemlélet szerepének korlátozása céljából alkotta meg az axiomatikus módszert.
Ragadjuk ki a szemléletből azokat a legegyszerűbb fogalmakat és e fogalmakról szóló legegyszerűbb, a szemlélet alapján félreérthetetlenül átlátható tételeket, amelyek szükségesek és elegendők a geometria megalapozásához. (Vagyis e szemléletből közvetlenül elfogadott fogalmakból és tételekből a további fogalmakat és tételeket már pusztán logikai úton lehessen felépíteni, anélkül, hogy a későbbiek folyamán a szemléletet ismét igénybe vennők.) Ezek az alapfogalmak és alaptételek felszívják a szemlélet szükséges elemeit. A belőlük alkotott alaprendszer már előírja a belőle levezethető egész geometriát.
Az euklidesi megalapozásban ilyen alap fogalmak például a pont, az egyenes, a távolság, stb. A róluk szóló első öt axióma pl. a következő:
 

  I.  Két különböző pont meghatároz egy egyenest.  II.  Az egyenes meghosszabbítható (az egyenes végtelen).  III.  Adott középpont és sugár meghatároz egy kört.  IV.  A derékszögek mind egyenlők.  V.  Két egyenes a közös szelőjük ama oldalán találkozik, amelyiken a ke-letkező belső szögek összege két derékszögnél kisebb.  
*

A geometriának axiomatikus megalapozása hatalmas szellemi munka. Az Elemek-ben már csak e munka termékét látjuk; az alapfogalmak és a róluk szóló axiómák állnak a könyv élén, s utána tüstént az euklidesi kor geometriai ismereteinek az alapokból való szigorú levezetése következik.
 

Euklides megtanította az emberiséget a kutatás exakt módszerére. A csodálatot hamarosan követte az első kritikai periódus. Ez a periódus a kritikában még csak a felszínen mozgott. Úgy találták a bírálók, hogy az V. axióma nem olyan közvetlenül átlátható és egyszerű, mint a többi. Mint például az első négy axióma. Megkísérelték hát egyszerűbben hangzó axiómával helyettesíteni. Így például azzal a tétellel, hogy a háromszög szögösszege két derékszög összegével egyenlő.
 

Az V. axiómából ez a tétel levezethető. De ha ezt a tételt választjuk az V. helyett axiómául, akkor ebből az V. vezethető le. Úgy mondjuk, hogy az V.-et vele aequivalens axiómával helyettesítjük. Ilyen aequivalens axiómákat a kétezer esztendős irodalomban bőven találhatunk. Most mutatóban felsorolunk néhányat.
 

1. Két párhuzamos egyenes távolsága mindenütt egyenlő (Poseidonius, I. század).
2. Adott egyenessel kívül eső ponton át csak egy párhuzamos egyenes van (Ptolemaios, II. század).
3. Van legalább két hasonló háromszög, amelyek nem egybevágók (Wallis, 1663).
4. Van legalább egy olyan háromszög, melynek szögösszege két derékszög összegével egyenlő (Saccheri, 1753).
5. Nincs maximális területű háromszög (Gauss, 1799).
6. Három különböző pont körön, vagy egyenesen van (Bolyai Farkas, 1851).
 

Ez a kritikai periódus lényeges fejlődésre nem vezetett. Az utána következő kritikai törekvések már sokkal mélyebbre irányultak. Az euklidesi axiómarendszerből töröljük az V. axiómát, s a megmaradóknak az összességét nevezzük röviden maradék‐rendszernek. Fölmerült a kérdés, vajon az V. axióma nem volt-e fölösleges? Az a sejtés alakult ki, hogy az V. axióma a többi axiómából levezethető, tehát az axiómarendszer fölösleges eleme. Ennek a sejtésnek a bizonyítására való törekvések meddők voltak.
 

Ezek a törekvések akkor mélyültek el, mikor indirekt úton próbálták a sejtést bizonyítani. Mit értünk a szóban forgó sejtés indirekt bizonyításán?
 

Fogadjuk el a maradék axiómarendszert és csatoljuk hozzá az V. axióma tagadását ‐ mondjuk abban a fogalmazásban, hogy a háromszög szögösszege nem minden háromszögre nézve =2R, vagy bármely más aequivalens fogalmazását is vehetnők. (Így például Bolyai Farkas azt az aequivalens fogalmazást választja, hogy az egyenestől állandó távolságú vonal görbe.) Induljon ki következtetéseink sora ebből a megváltoztatott axiómarendszerből. Ha ezen az úton ellentmondásra bukkanunk, akkor ezáltal bebizonyítottuk, hogy a szögösszeg nem minden háromszögre nézve =2R feltevés nem igaz.
 

Sok volt a hibás és meddő bizonyítási kísérlet. Az ellentmondásra vezető következtetés sehogy sem sikerült. Furcsa, a szemlélet számára szokatlan antieuklidesi geometriák bontakoztak ki a kutatások során, melyekben nem volt belső ellentmondás. A kutatók mégis inkább azt hitték, hogy elvétették a kutatómunka menetét, s ha majd kifogástalan munkát végeznek, fel fog merülni a várva várt ellentmondás.
 

A harmadik kritikai periodust Bolyai J., Gauss, Lobacsevszkij kutatásai jelentették.1 Helyesen felismerték és kiértékelték azt a tényt, hogy a maradék‐rendszerből és az V. axióma tagadásából kiinduló következtetések sora nem vezetett és nem is vezethet ellentmondásra. Mielőtt ennek a részletes taglalásába fognánk, ki kell térnünk Legendre (1794) tételére és e tétel bizonyítására. Ez a tétel arról szól, hogy az V. axióma tagadását a maradék‐rendszer, különösen az egyenes végtelenségét kifejező II. axióma miatt, bizonyos mértékben korlátozza.
 

Legendre‐tétel: A maradék axiómarendszerból már következik, hogy a háromszög szögösszege nem >2R.
Bizonyítás: Jelöljük a szögösszeget Σ-val. Bebizonyítjuk, hogy a maradék‐rendszerből és a Σ>2R föltevésből kiinduló következtetés ellentmondásig vezethető, tehát csak Σ≦2R lehet.
 

Legyenek 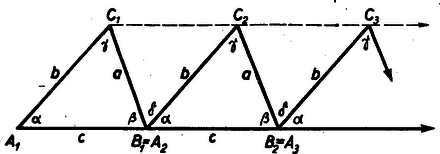A1B1C1, A2B2C2, ... egybevágó háromszögek. E háromszögek c=A1B1=A2B2=... oldalaikkal egy rétűen és hézagtalanul fedjék be az egyenest. Az ábrán a g egyenesre felrakott egybevágó háromszögek csatlakozásánál δ szögrés keletkezett. Fölmerül a kérdés, hogy bármely, A1B1C1 háromszög esetében is marad-e ki ilyen szögrés?
 
 
3. ábra
 

Euklides bebizonyította ‐ az V. axiómától függetlenül, az egybevágóság axiómáira támaszkodva ‐ hogy a háromszög bármely két szögének összege <2R. Tehát bármely háromszöggel csináljuk is meg az 3. ábra háromszög‐sorozatát, az α+β<2R miatt δ szögrések valóban fellépnek.
 

Nem mondhatjuk, hogy a C1, C2, ... szögpontok egy egyenesen sorakoznak, mert ez az V. axióma elfogadását követeli, de bebizonyítható, a maradék axióma‐rendszer alapján, hogy a C1C2, C2C3, ... egyenes‐szakaszok egyenlők.
Ugyanis a beékelt A2C2C1, A3C3C2, ... háromszögek δ-val jelzett szöge az eredeti háromszögek α és β szögével együtt megtölti a g egyenes egy‐egy pontjának félkörnyezetét. A beékelt háromszögek δ szögét bezáró oldalak pedig megegyezők, az eredeti háromszögek a, b oldalai. Így az első egybevágósági axióma szerint a megegyező δ szögükkel szemközti C1C2, C2C3, ... oldalak is egyenlők. Jelöljük ezeket d-vel.
No most tegyük fel, hogy a+β+γ>2R. Minthogy α+β+δ=2R, nyilván γ>δ. Az A1B1C1, és A2C2C1, háromszögek az a és b oldalban megegyezők, de a közbezárt szögükre nézve γ>δ áll. Ebből a szemközti oldalakra nézve c>d következik, aminek a bizonyítása már Euklides-nél is szerepel; ez a bizonyítás az V. axiómától független. Tehát c-d=e>0.
Most haladjunk A1-ből az Ak pontba. Az A1A2... Ak egyenes út rövidebb, mint az A1C1C2C2... CkAk törött útvonal. Vagyis
k⋅c<b+kd+b.
Innen
k⋅e<2b.
És ebben már képtelenséget állítunk. Hiszen ez azt jelenti, hogy bárminő nagy a k szám, az e szakasz k-szorosa nem érheti el az A1B1C1 háromszöggel előirt 2b távolságot.
Látjuk, hogy ez a bizonyítás mélyen kiaknázza a II. axiómát. Ez az axióma korlátozza tehát a szögösszegről szóló feltevést; eszerint a szögösszeg vagy=2R, vagy kisebb<2R-nél.1
Bolyai János abból indul ki, hogy semmi sem teszi indokolttá, hogy e lehetőségek közül az elsőt tüntessük ki azzal, hogy a geometria felépítésében alapul választjuk. A Σ<2R feltevésből és a maradék‐rendszerből kiindulva sem merül fel a következtetések során ellentmondás. A Σ=2R feltevésből pedig ugyancsak ellentmondás nélkül való geometria ‐ az euklidesi geometria ‐ következik. Indokolt tehát, ha a Σ≦2R-ben kifejezett két feltétel‐lehetőség egyikét sem tüntetjük ki, mint axiómát. Hanem pusztán a maradék‐rendszerből vezetjük le a geometriát. Ez a geometria, minthogy kevesebb axiómára épül, átfogóbb, mint az euklidesi. Ebben a geometriában tudjuk, hogy a Σ>2R nem teljesül, azonban a Σ közelebbi meghatározása közömbös. Ezt a ,,tágasabb'' geometriát nevezte el Bolyai abszolút geometriának: ezzel az elnevezéssel arra utal, hogy ez a geometria rendszer független attól, hogy az V. axiómát elfogadjuk, vagy tagadjuk.
Ha az abszolút geometriában a Σ=2R feltevést is bevezetjük, a geometria különös esetét, az euklidesi geometriát nyerjük. Ha pedig a Σ<2R feltevést választjuk, akkor a Bolyai által S-rendszernek nevezett geometriát nyerjük. Az S-rendszer tehát, a maradék axiómarendszerre és a Σ<2R axiómára épített geometriát, az ú. n. Bolyai‐Lobacsevszkij, vagy más néven hiperbolikus geometriát jelenti.
 

Bolyai nagy érdeme abban áll, hogy felépítette az abszolút geometriát és azon belül a hiperbolikus geometriát. Az egymásnak ellentmondó euklidesi és Bolyai‐Lobacsevszkij‐geometria az abszolút geometria szintézisében ,,egy kalap alá'' kerül. Ezzel pontot tett a kétezer esztendeig vajúdó kérdés után, visszavezetve az V. axióma függetlenségének kérdését a geometria ellentmondásnélküliségének problémájára.
A nem‐euklidesi geometria kialakulásának történetéhez hozzátartozik annak a megmutatása is, hogy miképpen bontakozott ki Bolyai János elméjében a nagy probléma, a probléma megoldásának helyes útja, az abszolút geometria felépítése. Mindezek a rendelkezésre álló dokumentumok alapján rekonstruálhatók.
 

Bolyai Farkas 1799-ben tért haza Göttingából. 1801-ben megnősült: 1804-ben meghívták a marosvásárhelyi kollégium matematika tanszékére tanárnak. A szerény jövedelmű, sovány lehetőségeket ígérő állást nagy örömmel fogadta. Hiszen akkor már elsőszülött fiának ‐ Jánosnak ‐ a sorsa, feleségének egészségi állapota követelte a szegényes, de mégis megnyugtató anyagi keretek biztosítását. 47 esztendőt töltött a katedrán, s még öt esztendőt nyugalomban.
János még Kolozsvárt született 1802 december hó 15-én. Gyermekkorának számottevő részét a marosvásárhelyi házban töltötte, amelyet Farkas természetbeni járandóság képen kapott. János nevelésére apja nagy gondot fordított, s az első rendszeres oktatásban is maga részesítette. Matematikára, vívásra, hegedűjátékra és a zenei ismeretek elemeire ő maga tanította. János gyorsan és sokat tanult, s a latin nyelvben is rohamosan haladt előre.
 

János már 15 éves korában ott tartott, hogy apjától ‐ ez Farkas véleménye volt ‐ nem volt mit, újat tanulnia. Jánosnak ebben az első életszakaszában, apjának hatása döntő tényező volt. Apjának matematikai érdeklődése, alapvető kérdések tisztázására való törekvése, mélyen és irányítóan befolyásolták a zseniális gyermek fejlődését. A párhuzamossági axiómához fűződő kétezer esztendős probléma iránti érdeklődés is, apja hatására vert benne erős gyökeret, Gauss iránti csodálata, határtalan tisztelete is ebben az időben ébredt, apjának elbeszélései nyomán.
Farkasnak az volt a vágya, hogy János Gaussnál folytassa szépen induló matematikai tanulmányait. A marosvásárhelyi tanár sanyarú anyagi körülményei ezt nem tették megvalósíthatóvá. Bár János a katonai pálya iránt nem érzett vonzalmat, a bécsi katonai mérnök akadémián folytatta tanulmányait. Ez volt élete első nagy csalódása, hiszen ő maga is Gausshoz vágyott, matematikát tanulni. 1818 augusztus 24-én vették fel az akadémia IV. osztályába.
Az akadémia matematikából nem sok újat nyújtott Jánosnak. Az egész képzés matematika anyaga a következő volt: a III. osztályban: aritmetika és algebra. A IV. osztályban: egyszerű geometria, sztereometria, a sík trigonometriája, gömbi trigonometria, geodézia és a térképezés elemei. Az V. osztályban: a kúpszeletek, magasabb fokú egyenletek megoldása, a differenciál- és integrálszámítás elemei, matematikai földrajz. A VI. osztályban: a szilárd és cseppfolyós testek mechanikája. Az utolsó ‐ VII. ‐ osztályban már matematikai jellegű tárgy nem is szerepelt.
János hamarosan az akadémia legkitűnőbb hallgatói sorába került, s arra is maradt ideje, hogy az V. axiómához fűződő problémán elmélkedjék. 1820 tavaszán apjának is megírta, hogy az axióma bebizonyításán fáradozik. Apja ‐ válaszlevelében ‐ aggódva igyekszik őt célkitűzéseitől eltéríteni, kevésbé meddő kérdésekkel való foglalkozásra kérlelni. Ámde ugyanebben a levélben arról is beszámol, hogy ő maga mennyit vergődött, hogy a problémát tisztázza és kitér saját elmélkedéseinek ismertetésére. Úgy, hogy az elterelésre szánt levél inkább lett ,,olaj a tűzre'', s János még izzóbb érdeklődéssel vetette magát a problémára.
Talán apja intő, aggódó sorai után vetett szikrát benne egy termékeny gondolat, mely az abszolút geometria kezdetét jelentette Bolyai János elméjében. Későbbi írásaiban visszaemlékezik erre az első szikrára. Azt írja, hogy még 1820-ban lépett arra az útra, amely az abszolút geometriáig elvezet. Magától rájött a Legendre-féle szögtételekre, s felmerült benne a kérdés, mi következménnyel jár a ,,háromszög szögösszege<2R'' feltevés. Először is a párhuzamosság fogalmának új értelmezését teszi szükségessé, ami pedig a végtelen sugarú körnek olyan szemléletére vezet, miszerint a végtelen sugarú kör nem egyenes, hanem görbevonal. Az egyenestől állandó távolságban futó pont pályája, a távolságvonal is, mint görbe mutatkozik az új szemléletben. Úgy fejezi ki ő maga, hogy a végtelen sugarú körnek a véges sugarú körhöz és a távolságvonalhoz való viszonya, a parabolának az ellipszishez és a hiperbolához való viszonyára emlékeztette.
 

Ez a termékeny sajátságos ötlet alapvető fontos mozzanat János gondolatvilágának kialakulásában. Egyben magárahagyottságának is első mozzanata. (Ezt a gondolatát apja már nem bírta követni, s csak akkor vált képessé végre megérteni a geometria nem‐euklidesi felfogását, midőn Gauss 1832. évi levele meggyőzte János alkotásának helyességéről és tudományos értékéről.)
 

Először is le kell szögeznünk azt a körülményt, hogy Bolyai János irodalmi tájékozottsága szegényes, a korabeli matematikai ismeretek teljessége szempontjából csak nagyon vázlatos volt. Még Gauss munkásságának eredményeit is csak kis részben ismerte. Így például Gauss felületelméleti kutatásairól ‐ a ,,Disquisitiones..,, című művéről ‐ élete végéig sem szerzett tudomást. Lobacsevszkijnek csak egyetlen művéről ‐ de arról is csak később ‐ 1848-ban értesült. Nyilvánvaló, hogy ez a viszonylagos tájékozatlanság csak fokozta azokat a nehézségeket, amelyek Bolyai elé tornyosultak. A tudós környezet ösztönző hatása, a rokon problémakörben működő kutatók érdeklődése, más kutatók módszereinek megismerése az eredményes és szívós kutatómunkának szilárd támaszai, erős mozgatói. Bolyainak mindebben nem volt része.
 

Az első írásos dokumentum, amelyből következtetni lehet Bolyai gondolatvilágának fejlődésére, 1820-ból való. Egyik VI. osztályos mechanika füzetében, ,,A Parallelarum Theoria'' felirattal.
 

Bolyaiban a geometriai szemlélet átalakulása megindult. 1823-ban egy téli éjszakán végül is megállapította azt az összefüggést, amely az ú. n. párhuzamossági szög és párhuzamossági távolság között fennáll.1 Kutatásainak során ez volt a második döntő mozzanat. A felismerés boldog örömében, a kutató munkának elég általános tünete képen, felvillant előtte a nem‐euklidesi geometria felépítésének teljes körvonala. A végleges forma villanásszerű megsejtése vezette tollát, midőn 1823 november 3-án nevezetes levelét megírta apjának.
 

≫...semmiből egy újj más világot teremtettem. Mind az, valamit eddig küldöttem, csak kártyaház a toronyhoz képest. Meg vagyok győződve, hogy nem sokkal fog kevesebb betsületemre szolgálni, mintha fel‐találtam volna.≪
Apja válaszában igyekszik János lelkesedését lelohasztani. Félti, mert képtelen elhinni, hogy fia új utat talált, mely elvezeti a kétezer esztendeje vajúdó probléma tisztázásához.
János 1825 februárjában Marosvásárhelyre megy apjához, látogatóba. Részletesen megmutatta akkor az abszolút tértudomány felépítését. Apja formálisan megértette, helyesebben tudomásul vette és követte János gondolatait, de lényegét és jelentőségét nem bírta felfogni, mert képtelen volt a belécsontosodott euklidesi szemléletet szétfeszíteni. Heves viták után János szomorúan távozott. Vágyott apja elismerésére és szomorúsággal töltötte el az a felismerés, hogy messze szakadtak egymástól, mert föléje nőtt s apja képtelen hozzá felemelkedni.
1826-ban a ≫egy 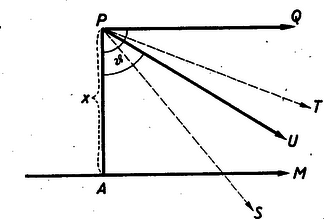írásbeli dolgozatot≪ adott át Bolyai egykori tanárának, Wolter századosnak. Ebben az abszolút geometriának ≫az alapja le van téve≪ (Bolyai János kézirataiból merített adatok.) Sajnos ez a Wolternek küldött kézirat nem került elő.
Ha a Σ<2R feltevésből indulunk ki, akkor következik, hogy van az AM→-et sehol sem metsző olyan PT→ egyenes is, melyre nézve APT∢ hegyesszög, sőt számtalan ilyen nem‐metsző van. (4. ábra)
 
 
4. ábra
 

Bolyai párhuzamosnak nevezte ama nem‐metsző PU→ félegyenest, amelyre nézve teljesül az, hogy minden az APU∢-beli PS→ félegyenes metszi az AM-et. (Persze az UPQ∢-beli egyik PT→ egyenes sem metszi AM→-et.)
Az APU∢=ϑ szöget az x párhuzamossági távolsághoz tartozó párhuzamossági szögnek nevezzük. Bolyai 1823 telén fedezte fel azt a nevezetes tételt, miszerint
cotgϑ2=exk
ahol e a természetes logaritmus alapszáma és k valamely pozitív érték, ami csak empirikus alapon határozható meg. Ha a mérések azt igazolnák, hagy a k végtelen nagy, akkor a valóságban az euklidesi geometria volna érvényes és ϑ/2=45∘ volna.
A legpontosabb mérések sem bizonyítottak többet, minthogy a k óriási nagy érték, s így a ϑ/2=45∘ a gyakorlat szempontjából tökéletesen pontosnak tekinthető és a geometria euklidesi rendszere a valóságos tér leírására tökéletesen alkalmas. Azonban az óriási méretű világtérben a 45∘-nak legkisebb híja is azzal járna, hagy a k óriási nagy, de mégis véges és így a világtérben, nagyban a Bolyai‐Lohacsevszkij‐geometria érvényesülne.
Bolyai Farkas mintegy húsz esztendeje dolgozott már élete fő művén, melynek kinyomtatására 1829-ben kapta meg az engedélyt. Két kötetben jelent meg, az első kötet 1832-ben. János 1830 őszén találkozott ismét apjával, s valószínűnek látszik, hogy az akkori megbeszélés alapján elhatározta az abszolút geometria rövid, írásban való kifejtését. Latin nyelvű kéziratát 1831-ben adta át apjának, hogy megjelenőben levő könyvéhez, mint annak egyik függelékét csatolja. Farkas szóbanforgó művének címe ≫Tentamen juventutem studiosam in elementa Matheseos...introduceadi≪ Az első kötethez csatolt három függelék egyike a János műve. A függelék címe: ≫Appendix scientiam spatii absolute veram exhibens: a veritate aut falsitate Axiomatis XI. Euclidei, a priori haud unquam decidenda indipendentem: adjecta ad casum falsitatis quadratura circuli geometrica≪. Röviden csak Tentamen, ill. Appendix e művek közismert címe. Az Appendix különlenyomatai már 1831 június havában elkészültek.
Bolyai Farkas elküldte az Appendixet Gaussnak és fia nevében kérte véleményét. Gauss nevezetes válasza 1832 március 6-án kelt. Farkas másolatot készített róla és elküldte Jánosnak Lembergbe. János április 6-án kapta meg a levelet.
Gauss levele az első avatott személy bírálata. Hűvös hangja ellenére mély elismerést is kifejez.
≫Most valamit a fiad munkájáról. Ha avval kezdem, hogy nem szabad megdicsérnem, bizonyára egy pillanatra meghökkensz, de mást nem tehetek, ha megdicsérném, ez azt jelentené, hogy magamat dicsérem, mert a mű egész tartalma, az út, melyet fiad követett és az eredmények, amelyekre jutott, majdnem végig megegyeznek részben már 30‐35 év óta folytatott meditatióimmal. Valóban ez rendkívül meglepett engem.
 

Szándékom volt, hogy saját munkámból, melyből egyébiránt mostanáig csak keveset tettem papírra, életemben semmit sem bocsátok nyilvánosságra: A legtöbb embernek nincs meg a helyes érzéke az iránt, amin ez a dolog múlik s én csak kevés olyan emberre akadtam, aki azt, amit vele közöltem, különös érdeklődéssel fogadta. Erre csak az képesít, hogy élénken érezzük, hogy mi az, ami tulajdonképpen hiányzik, és ami ezt illeti a legtöbb ember nincsen vele tisztában. Ellenben az volt a szándékom, hogy idővel mindent úgy írjak meg, hogy legalább majdan velem el ne pusztuljon.≪
≫Nagyon meglepett tehát, hogy a fáradtságtól már most megkímélhetem magamat és nagyon örvendek, hogy éppen régi jó barátom fia az, ki engem olyan csodálatos módon megelőzött ...≪
≫Éppen annak lehetetlensége, hogy a priori Σ és S között dönthessünk, legvilágosabb bizonyítéka annak, hogy Kantnak nem volt igaza, midőn azt állította, hogy a tér csak formája a mi szemléletünknek. Más éppen olyan erős okra, egyik kis dolgozatomban mutattam rá, mely a Gött. Gel. Anzeigen 1831. évi kötetében található, mint 64. darab a 625. oldalon. Talán nem fogod megbánni, ha abban fáradozol, hogy a G. G. A. ezt a kötetét megszerezd (ami bármelyik bécsi, vagy budai könyvkereskedő útján történhetik), mert benne találod néhány oldalon kifejtve a képzetes mennyiségekre vonatkozó nézetemnek lényegét is.≪
 

Gauss levelének nyilatkozata erősen emlékeztet más nyilatkozatára, amelyet Jacobi és Abel ‐ az elliptikus függvények elméletében alapvetően fontos ‐ vizsgálataira vonatkozólag tett. Legendre nagyra tartotta Abel munkásságát, s Gauss nyilatkozata felháborította. Hasonlóképpen Bolyai János is megütközött Gauss magatartásán. Nem arra volt szüksége, hogy művének értékes voltát Gauss is kifejezze, erre csupán Farkas meggyőzése végett vágyott. Ezt meg is kapta. Ő maga szilárd meggyőződéssel vallotta, tudatosan tudta, hogy óriási értékű művet alkotott. Bolyai elismerésre, odaadó támogatásra vágyott, s Gauss úgy nyilatkozik, hogy szép‐szép, de én ezt már megcsináltam.
Vajjon szabad-e ≫méltánytalan≪ viszontbírálatnak minősíteni Bolyai János következő sorait.
 

≫Nézetem szerint és mint erősen meg vagyok győződve, minden elfogulatlanul ítélőnek nézete szerint, mindazok az okok, melyeket Gauss arra felhoz, hogy miért nem akart e tárgyra vonatkozó dolgozataiból életében mit sem közölni, erőtlenek és semmisek, mert hisz a tudományban úgy, mint magában a közönséges életben, mindig arról van szó, hogy szükséges és közhasznú, de még homályos dolgokat kellően tisztázzunk és az igaz és helyes iránt még hiányzó, vagy még inkább szunnyadó érzéket felkeltsük, kellően eddzük és előmozdítsuk. A matematika iránti érzék általában az emberiség nagy kárára és hátrányára, fájdalom csak igen kevés emberben ébred; és ilyen okból, vagy ürügyből Gaussnak, hogy következetes maradjon, kitűnő műveinek még igen jelentékeny részét magánál kellett volna rejtenie. És az a körülmény, hogy fájdalom, a matematikusok között mégpedig a híresek között is, nagy számmal vannak felületesek, értelmes embernek nem szolgálhat okul arra, hogy csak felületest és középszerűt alkosson és a tudományt lethargikusan csak az örökölt állapotban hagyja. Efféle feltevés egyenesen természetellenesnek és merő oktalanságnak nevezhető; és ennélfogva annál inkább zokon esik, ha Gauss ahelyett, hogy az Appendix és az egész Tentamen nagy becsét egyenesen, nyíltan elismerte volna és nagy örömét és érdeklődését nyilvánítva, arra törekedett volna, hogy a jó ügynek illő fogadtatást szerezzen, inkább mindezek elől kitérve csak jámbor kívánságokkal és a kellő műveltség hiánya fölötti panaszokkal érte be. Bizony nem ebben áll az élet, a munkálkodás és az érdem.≪
 

Hasonló hangulatot tükröznek következő sorai is, melyeket 1832-ben egy folyamodványában írt.
 

≫Az egyetlen Gauss, úgy látszik, tett néhány könnyebb lépést a cél felé, de még nagyon messze volt attól, hogy ezt magát lássa. De minden fáradozása dacára sem tudott előrehaladni, ezt a szerző kétségtelenné tudja tenni több adattal, melyet Gaussnak részint mostani, részint előbbi és az apjának számos (a szerzőhöz intézett) levele tartalmaz. A szerző minden benne fölmerülő főnehézséget már az 1823. év második felében győzött le, miután már előbb, mikor még szerencséje volt a cs. k. mérnök‐akadémia növendékének lenni, minden valódi tudás és különösen az ilyen ‐ fontosságtól és nevezetességétől eltekintve ‐ már történetileg is annyira rendkívüli tárgy iránt oly élénk érdeklődést ébredt benne, hogy néhány könnyed kísérlet után, mely még távol elmaradt a céltól, nem rettent vissza egy erőteljes támadás fáradalmaitól, hogy ezt a nagy és annyira ki nem elégítő hézagot betöltse. És mélyen érzi, hogy nyugalmat és boldogságot nem talál addig, míg a labyrinthushól ki nem tekergőzik.≪
Bolyai lendületét, munkakedvét, erejét a csalódások s betegsége is hosszú időre megtörték. Esztendők peregtek le egymás után anélkül, hogy alkotó erejét bármiféle problémára irányította volna.
 

Gauss magatartása Bolyai Jánossal szemben nem volt méltó ahhoz a hatalmas tudományos tekintélyhez, amelyet alkotó munkásságával önmaga számára kivívott. Nem érezte át azt az erkölcsi kötelességet, hogy a nagy felfedezésre felhívni a tudós világ figyelmét, segíteni az ismeretlen tudóst a kibontakozás útján azoknak a feladata, akik már felérkeztek a legmagasabb csúcsra, akiknek az elismerő szava másoknak is súlyt ad.
Bolyai János későbbi elmélkedési során az abszolút geometria további kidolgozásában még igen fontos eredményekre jutott. Az Appendix egyetlen nyomtatásban megjelent műve, hosszú ideig más eredményeit nem is ismerték.
Élete végéig megmaradt elszigeteltségében. Nem az ő hibája, hanem kora társadalmi állapotáé. Sanyarú sorsára jellemző, hogy egy valamire való könyv sem akadt kezébe. Más matematikusok gondolatai nem jutottak el hozzá. Mégsem sorvadt el alkotó ereje. Gondolatai ‐ kizárólag önmagából merítve is ‐tovább fejlődtek. A térfogalom tisztázásában oly messzire jutott, ahová csak a XIX. század végén érkeztek el más, és szerencsés tudományos környezetben dolgozó kiváló matematikusok.
Hatalmas szellemi erőre vall az a tény, hogy anyagi nyomorban, szörnyű elszigeteltségben is tovább dolgozott, önmaga számára, élete végéig. Az ilyen életet ritka ember bírja ki törés nélkül. Bolyai János pedig a matematika más területein is súlyos és mély problémákat vetett fel, s nem egy ilyen problémának a megoldására vezető utat vázolta, vagy kifejtette feljegyzéseiben.
Sőt a matematika határán túl, más problémák is izgatták örökké kutató elméjét. Társadalmi problémák. Ez irányú eszméi annak a sivár társadalmi környezetnek a benne ütött sebeiből fakadtak, melyben végigvergődte tragikus életét. Az egyéni sors kegyetlen ütései nem sirámokat fakasztottak ajkán, hanem az emberibb, igazságosabb társadalmi rendszer alapvető problémáinak kutatására sarkalták.
 

Bolyai Jánost fiatalon, 1833-ban nyugdíjazták. Sanyarú anyagi viszonyok között tengődött élete végéig, meg nem értő, kicsinyes, gyötrő környezetben. Elismerésben sohasem volt része ‐ hiszen Gauss hallgatott ‐ munkásságáról csak halála után szereztek tudomást a matematikusok. Környezete még másban sem értette meg, ugyan ki értette volna közülük korszakalkotó tudományos kutatásait! Teljesen elhagyottan halt meg 1860 jan. 17-én. A marosvásárhelyi temetőbe temették. Midőn a múlt század végén ‐ az akkor már világhírű ‐ Bolyai János sírját keresték, hogy emlékkövet állítsanak, alig találtak rá az elfelejtett, jeltelen sírra.
Gauss nagy tanítványának, Riemannnak bizonyos fölfedezése váltotta ki a matematikusok olyan irányú érdeklődését, mely Bolyai és Lobacsevszkij felfedezését az ismeretlenségből kiemelte. Továbbá Gauss hagyatékának rendezése során merült fel a kérdés, ugyan ki az a magyar matematikus, akit a hűvös fejű, a dicséretben oly fukar szavú  textitGauss, zseniális matematikusként emleget néhány levelében.
1868-ban J. Hoüel francia nyelvre fordította az Appendixet, megtoldván a két Bolyai életrajzával. 1872-ben Frischauf német nyelven, tankönyvszerű feldolgozásban ismertette Bolyai János abszolút geometriáját. A rohamosan terjedő érdeklődés során világhírre emelkedett az Appendix. 1891-ben G. B. Halsted austini (Texas) professzor angolra fordította, történeti bevezetést írt hozzá. Könyve 1896-ban már a negyedik kiadást érte meg. Maga Halsted csupán azért kelt át az Óceánon, hogy Bolyai sírját felkeresse.
1902 január 27-én a Magyar Tudományos Akadémia Bolyai‐díjat létesített. Első alkalommal H. Poincaré (1905), második alkalommal D. Hilbert (1910) részesült Bolyai‐díjban.
A Sztalin‐díjas V. F. Kagan professzor 1950-ben orosz nyelvre fordította az Appendixet, bőséges életrajzzal és magyarázatokkal látta el (234 lap).
Ma már az egész világ elismeri Bolyai János nagyságát, s mi boldog büszkeséggel készülünk születése százötvenedik évfordulójának megünnepelésére.
1V. ö. Alexits‐Fenyő: ,,Matematika és dialektikus materializmus''.

1V. ö. Kárteszi: ,,Az olló geometriája''. 19., 20, 21. §.

1Bolyai-tól függetlenül a kazáni egyetem zseniális professzora N. I. Lobacsevszkij (1792‐1856) szintén megoldotta a párhuzamosságra vonatkozó kétezer esztendős problémát, s felfedezte az anti‐euklidesi geometriát. Felfedezését több könyvben is részletesen kifejtette. Ezért nevezi az irodalom a hiperbolikus geometriát ‐ később szó lesz róla ‐ Bolyai‐Lobacsevszklj geometriának.

1Könnyen levezethető Legendre másik szögtétele is: ha egy háromszög szögösszege=2R, akkor minden háromszögnek a szögösszege=2R; ha pedig egy háromszög szögösszege<2R, akkor minden háromszög szögösszege <2R.

1Ha Σ=2R feltevésből indulunk ki; akkor ,,az AM→ félegyenest a P-ből kiinduló minden félegyenes metszi, kivéve azt az egyetlen PQ→ félegyenest, mely az AM-re merőleges AP→-vel derékszöge zár be'' tételt levezethetjük. Megfordítva a dolgot: ebből a tételből, mint feltevésből a ≫Σ=2R≪ tétel gyanánt levezethető.