Cím: Az 1951. évi Arany Dániel matematikai tanulóversenyről beszámoló
Füzet: 1951/november, 105 - 113. oldal  PDF  |  MathML 
Témakör(ök): Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A verseny lefolyását és a feladatok szövegét előző számunkban már ismertettük. Az alábbiakban közöljük az eredményeket és az első forduló feladatainak a megoldását. A második forduló feladataira következő számunkban térünk vissza. Az első forduló feladataira adott megoldások a döntőbe jutást biztosították. A helyezések a második fordulóban elért eredmény alapján történtek.

 

A kezdők versenyén az algebrai átalakítás bizonyult a legnehezebb feladatnak. Hibátlan megoldást egyedül Kántor adott rá. Lényegében jó Bársony megoldása is; azonban megoldásába előjelhiba került. A második feladatra négyen adtak lényegében helyes megoldást. A harmadik feladatot majdnem mindenki megoldotta. Sokféle megoldás érkezett. A megoldhatóság feltételét is többen megállapították. Kántor azt is észrevette, hogy szerkesztése kétféleképpen hajtható végre, tévesen vélte azonban, hogy ezúton két különböző pontot szerkeszthetne.
A bíráló bizottság Kántor Sándor, a debreceni református gimnázium II. oszt. tanulója dolgozatát I. díjban, Bársony András, a nagykanizsai Irányi Dániel gimnázium II. oszt. tanulója dolgozatát II. díjban, Kovács László, a debreceni református gimnázium I. oszt. tanulója és Zobor Ervin, a nagykanizsai Irányi Dániel gimnázium II. oszt. tanulója dolgozatait pedig egy‐egy III. díjban részesítette.
 

A haladók versenyén legtöbb nehézséget a térmértani feladat adott. Hogy hétélű test nincs, azt többen nem is próbálták bizonyítani. A bizonyításhoz legközelebb talán Villányi jutott, azonban Euler‐féle testekre szorítkozott és leírása zavaros. A megoldás első részében Kováchnak van egy szellemes gondolata, bár leírása nem világos. Az exponenciális egyenletrendszernél egyedül Villányi látta helyesen az x=y=1 megoldást. László észrevette ugyan e megoldás létezését, de nem látta, hogyan következik az az ő levezetéséből. Ehelyett utólag egy teljesen hibás eljárással erőszakolta ezt ki. Érdeme viszont, hogy a második feladatra két különböző, egyszerű megoldást adott. E feladatot elég sokan megoldották, de a megoldások egyszerűségében és áttekinthetőségében igen nagy különbségek vannak. Figyelemreméltó Mórenth dolgozata, mely arra mutat, hogy viszonylag kis gyakorlottsággal, de a problémák lényegének világos meglátásával jut el eredményeihez.
A bizottság Villányi Ottó szentendrei gimn. III. oszt. tanulója dolgozatát I. díjban, László Zoltán, a debreceni Fazekas gimn. IV. oszt. tanulója dolgozatát II. díjban, Kovách Ádám, a nyíregyházi Kossuth gimn. IV. oszt. tanulója, és Mórenth András, a budapesti I. ker. dolgozók gimn. IV. oszt. tanulója dolgozatát III. díjban részesítette. Ezen kívül dicséretet nyert első helyen Marosfalvi László (szombathelyi Nagy Lajos gimn. IV. oszt.) és Schay Géza, (budapesti József Attila gimn. III. oszt.): második helyen Heppes Aladár (kaposvári Táncsics gimn. IV. oszt.), Kálmán Lajos (budapesti Berzsenyi Dániel gimn. III. oszt.) és Rejtő Péter (budapesti református gimn. III. oszt.).
A nyertesek pénzjutalmat, a dicsértek pedig ajándékkönyvet kaptak.
 

Az első forduló feladatainak megoldása

 

Kezdők feladatai:
 

1. Hozzuk egyszerűbb alakra az
(x+y)5xy(x2+xy+y2)-x4y(x2+xy+y2)-y4x(x2+xy+y2)
kifejezést.
A feladatot legtöbben osztási eljárással oldották meg. Ez az eljárás azonban nem sokat segít, ha a tört egyszerűsíthető, de nem az egész nevezővel. Célszerűbb megpróbálni közös nevezőre hozatal után a számlálót és nevezőt is lehetőségig szorzattá alakítani.
 

Megoldás. A törtek közös nevezője xy(x2+xy+y2) és közös nevezőre hozva a számláló
(x+y)5-x5-y5=(x+y)5-(x5+y5).

Mint teljes indukcióval, könnyen belátható, két egyenlő páratlan kitevőjű hatvány összege felírható mint az alapok összege, szorozva egy polinommal1:
a2n+1+b2n+1=(a+b)(a2n-a2n-1b++a2n-2b2-...-ab2n-1+b2n).


Ezt használva n=2-re, a számláló így alakítható:
(x+y)5-(x5+y5)=(x+y)[(x4+4x3y+6x2y2++4xy3+y4)-(x4-x3y+x2y2-xy3+y4)]==5(x+y)xy(x2+xy+y2).


Így az egész nevezővel lehet egyszerűsíteni és a kifejezés legegyszerűbb alakja 5(x+y) lesz.
 

2. Bizonyítsuk be, hagy bármely háromszög magassági pontjának az oldalak felezőpontjára vonatkozó tükörképei a háromszög köré írt körön vannak.
 

I. megoldás. Ha az egyik oldal középpontjára tükrözünk, akkor a magassági pont, a tükörképe és a kérdéses oldal végpontjai olyan négyszöget alkotnak, melynek átlói felezik egymást, tehát paralelogrammát.
 
 

Ennek a tükrözött pontba futó oldalai merőlegesek egy‐egy háromszögoldalra, mert a paralelogramma velük párhuzamos oldalai a háromszög magasságai. Így a háromszög csúcsai és a magasságpont tükörképe olyan négyszöget alkotnak, melynek két szemközti szöge derékszög. Ez a négyszög tehát húrnégyszög. Így a háromszög köré írt kör átmegy a magassági pont tükörképén. A meggondolás hegyes és tompaszögű háromszögre egyformán alkalmazható.
 

II. megoldás. Eljárhatunk fordítva is. A magasságpontot összekötjük az oldal felezőpontjával és meghosszabbítjuk az egyenest a körig.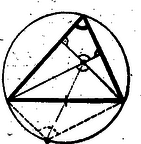
 
 

Ekkor a keletkező metszéspontról kell megmutatni, hogy az a magassági pontnak a felezőpontra vonatkozó tükörképe, vagyis, hogy az oldal középpontja felezi a magassági ponttól a körig terjedő szakaszt is. Ez esetben az e két pont és a kérdéses oldal végpontjai által meghatározott négyszög paralelogramma. Ezt fogjuk bebizonyítani.
Az egyíves szögek, mint csúcsszögek egyenlők. A felső 180∘-ra egészíti ki a háromszög kövéríves szögét, mert e szögek szemköztes szögei egy olyan négyszögnek, melynek másik két szöge derékszög. A kövéríves szöget a szaggatott ívű szög is 180 fokra egészíti ki, mert olyan kerületi szögek, melyeknek ívei egymást teljes körré egészítik ki. Így a kérdéses négyszögről azt tudjuk, hogy két szemközti szöge egyenlő és az ezek csúcsát összekötő átló felezi a másik átlót. A 329. feladat (97. old.) megoldása szerint az ilyen négyszög valóban paralelogramma.
 

III. megoldás. Ismerünk (az I. gimn. új tankönyvéből pl.) egy hasonló tételt: A magassági pontnak az oldalakra vonatkozó tükörképei a körülírt körön vannak.
 
 

Ezt felhasználva is bizonyíthatjuk a tételt. Azt kell felhasználnunk, hogyha egy pontot egymásután tükrözünk két egymásra merőleges egyenesre, akkor a pontnak a tengelyek metszéspontjára vonatkozó tükörképéhez jutunk. Esetünkben a magassági pontnak az oldalra vonatkozó tükörképét még az oldal középmerőlegesére kell tükröznünk. Ez az egyenes azonban átmegy a körülírt kör középpontján, s így tükörtengelye a körnek. Az e körüli tükrözés tehát a középpontra vonatkozó tükörpontba, másrészt ismét a körülírt körön fekvő pontba viszi át a magasságpontnak az oldalra vonatkozó tükörképét.
 

IV. megoldás. Rajzoljuk meg mindhárom tükörpontot.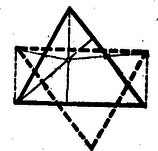
 
 

Az ezek meghatározta háromszög egybevágó az eredetivel és hozzá képest 180∘-kal el van forgatva, mert úgy keletkezett az oldalfelezőpontok alkotta háromszögből, hogy azt a magassági pontból, mint középpontból kétszeresre nagyítottuk. Meg fogjuk mutatni, hogy a két háromszög oldalfelező merőlegesei egybeesnek, vagyis, hogy két‐két egyenlő oldal végpontjai téglalapot határoznak meg. Vizsgáljuk a vastagított oldalt. Azok az egyenesek, amelyek ennek végpontjait kötik össze a másik két oldal középpontjára vonatkozó tükörképekkel, párhuzamosak és egyenlők a vastagított oldalra bocsátott magasságnak a háromszögcsúcs és a magassági pont közti szakaszával, mert ennek tükörképei egy‐egy oldalközéppontra nézve. Így merőlegesek a vastagított oldalra. A kérdéses négyszög tehát valóban téglalap.
 

Megjegyzés. Rajzoljuk meg a körülírt kört és a magassági pontnak a ráeső hat tükörképét.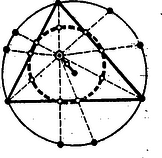
 
 

Ha a kört most a magassági pontból felére kicsinyítjük, akkor az oldalra vonatkozó tükörképek a magasságok talppontjára fognak kerülni, az oldalközéppontra vonatkozó tükörképek pedig az oldalközéppontra. E hat pont tehát egy körön van. Ennél az összehúzásnál a háromszögcsúcsok a magasságokon a csúcs és magassági pont közti szakasz felezőpontjába fognak kerülni. Ezekkel együtt 9 nevezetes pontot találtunk a háromszögben, melyek egy körön vannak. Ezt a kört a háromszög Feuerbach‐féle körének nevezzük. A feles kicsinyítésből az is következik, hogy a Feuerbach‐kör középpontja középpontja a magasságpont és a körülírt kör középpontja közti szakasznak is. Az e három ponton átmenő egyenest Euler‐egyenesnek nevezik és megmutatható, hogy ezen rajta van a súlypont is.
Az I. megoldásból a Feuerbach‐körre vonatkozó állítások egy egyszerű bizonyítása is adódik. Rajzoljuk meg a magasságvonalakra eső pontok alkotta háromszöget és kössük össze az egyik oldal végpontjait a párhuzamos háromszögoldal középpontjával.
 
 

Ekkor e háromszögoldal és a magasságpont alkotta háromszögben meghúztuk mindhárom középvonalat. Így a szaggatott négyszög két szemközti szöge derékszög lesz, tehát a kis háromszög köré írt kör átmegy a nagy háromszög oldalainak középpontján. Az oldalközéppontot a kis háromszög szemközti csúcsával összekötő egyenes e körnek átmérője. Mivel ez a szakasz a magasság talppontjából is derékszög alatt látszik, így e talppont is a körön van.
 

3. Az a, b, c, d számok milyen értékei mellett van megoldása és hányféle megoldása van az
x+y=a,y+z=b,z+u=c,u+x=d
egyenletrendszernek?
A feladat meglepően sok nehézséget adott a versenyzőknek. A megoldhatóság feltételét még sokan megtalálták, de hogy ez mit jelent, azt kevesen tudták megmagyarázni; a megoldások számára vonatkozó kérdéssel pedig a legtöbben értetlenül álltak szemben.
 

Megoldás. Összeadva egyrészt az első és harmadik, másrészt a második és negyedik egyenletet az
x+y+z+u=a+c,ésy+z+u+x=b+d
összefüggéshez jutunk. Ez csak akkor nem jelent ellentmondást, ha a+c=b+d. Ez tehát a megoldhatóság feltétele. Ha ez teljesül, akkor bármely három egyenletből következik már a negyedik. Így elég három egyenlet megoldását keresni. Ilyen esetben egy változót tetszés szerint választva a többi általában egyértelműen kiszámítható. Esetünkben ez mindig így van. Válasszuk pl. u-t tetszés szerint. Ekkor a harmadik, második és első egyenletből sorra z=c-u, y=b-c+u, x=a-b+c-u(=d-u) adódik. Ez esetben tehát az egyenletrendszernek végtelen sok megoldása van.
 

Megjegyzés. Ha pl. az összeg konstansok pozitívok, akkor a feltétel éppen azt fejezi ki, hogy ha a, b, c, d hosszúságú pálcákból (ebben a sorrendben) négyszöget rakunk össze úgy, hogy a pálcák az összeillesztési pontok körül egymáshoz képest elforgathatók legyenek, akkor e négyszög minden állásában, ha konvex, akkor érintő négyszög. Az egyenletek ez esetben a csúcsoktól az érintési pontokig terjedő szakaszokat szolgáltatják. Ezek a különböző négyszögállásoknál változnak. Így ez a meggondolás is mutatja, hogy végtelen sok gyök van.
 

Haladók feladatai:
 

1. Oldjuk meg a
2(x+1)22(x-1)2=4x2
egyenletet.
 

Megoldás. Az egyenlet így alakítható át: 24x=22x2, és ez csak úgy állhat fenn, ha a kitevők egyenlők. A keletkező egyenletet nullára redukálva, a 2x2-4x=2x(x-2)=0 egyenletre jutunk, és mivel szorzat csak úgy lehet nulla, ha valamelyik tényezője nulla, így az x=0 és x=2 megoldások adódnak. Azonnal látható, hogy ezek az eredeti egyenletnek valóban megoldásai is.
 

Megjegyzés. A versenyzők a másodfokú egyenletet ‐ ritka kivétellel ‐ vagy elosztották 2x-szel és csak egy gyököt kaptak; vagy eljutottak a két gyökhöz, de csak az oldó képleten át. Mindkét eljárás arra mutat, hogy gondolkodás nélkül, gépiesen dolgoznak.
 

2. Egy egyenlőszárú trapéz párhuzamos oldalainak a hossza 15,3 és 25,2 cm. A hosszabbik párhuzamos oldal végpontjaiból a rövidebbik olyan szög alatt látszik, amelynek tangense 0,75. Számítsuk ki a trapéz területét.
Itt ismét sok fölösleges számítástól és számítási hibától menekült volna meg, aki helyesen tudja használni algebrai ismereteit. Ilyen azonban egy sem akadt a versenyzők közt. Igen sok út kínálkozik a magasság kiszámítására, de mindegyik több‐kevesebb mellékszámításon át vezet. Ilyenkor célszerű az adott mennyiségeket alkalmas betűkkel jelölni és a számértéket majd csak a területre nyert kifejezésekbe helyettesíteni be. Esetünkben, mivel a trapéz szimmetrikus, a párhuzamos oldalak felét célszerű jelölni pl. a-val és b-vel (a>b), az adott tangens legyen t, a látószöget jelöljük α-val.
Ekkor a trapéz középvonala a+b és csak az m magasságot kell kiszámítanunk.
 

I. megoldás. Legyen a hosszabb párhuzamos oldal végpontjából a szemközti szár látószöge 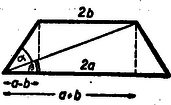β.
 
 

Mivel egyenlőszárú trapéz rövidebb párhuzamos oldalának végpontjából húzott magassága a szemközti oldalt a+b és a-b hosszúságú darabokra osztja, kapjuk a tg (α+β)=ma-b; tg β=ma+b összefüggést. Ezeket a tg (α+β)=tg α+tg β1-tg α tg β kifejezésbe helyettesítve az
ma-b=(t+ma+b)(1-tma+b)
egyenletet kapjuk, mely rendezés után m-re az
m(a+b-tm)=(a-b)(t(a+b)+m),
vagy
tm2-2bm+t(a2-b2)=0
másodfokú egyenletet szolgáltatja. Ennek gyökei
m=bt±(bt)2-(a2-b2)=bt±b2(1+1t2)-a2bt=10,2;a2-b2=(a+b)⋅(a-b)=20,25⋅4,95=100,2375;(bt)2-(a2-b2)=1,95.

Innen m1=8,35; m2=12,15; és a terület: T1=169,0875; T2=246,0375.
 

II. megoldás. Az egyenlőszárú trapéz körbe írható. Hosszabbítsuk meg az egyik magasságot a körig. A meghosszabbítást jelöljük 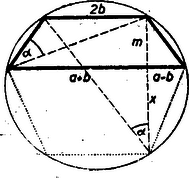x-szel.
 
 

A meghosszabbítás végpontjából a 2b hosszúságú oldal szintén α szög alatt látszik, tehát t=tg α=2bm+x. Másrészt az egy ponton átmenő húrok szeleteit számítva m⋅x=(a+b)(a-b)=a2-b2. Az első egyenletet így is írhatjuk: m+x=2bt. Ismerjük m és x összegét és szorzatát, tehát e két mennyiség az
u2-2btu+a2-b2=0
egyenlet két gyöke. Ez lényegében megegyezik az előző megoldásban nyert egyenlettel és így ugyanazokhoz az eredményekhez is vezet. Akármelyik gyököt választhatjuk m-nek, amit az magyaráz, hogy a rajzon pontozva jelzett trapéz is megfelel a feltételeknek.
 

III. megoldás. Még egyszerűbben jutunk a megoldáshoz, ha megrajzoljuk a 2b hosszúságú oldalhoz tartozó középponti szöget a trapéz köré írt körben.
 
 

Ennek nagysága 2α, tehát ha a kör középpontjából a 2b hosszúságú oldalra merőlegest bocsátunk, derékszögű háromszöget kapunk, melynek egyik hegyesszöge α és a szemközti befogója b. Így az oldal távolsága a kör középpontjától x=bt, a kör sugara pedig r=b2+b2t2=b1+1t2. A hosszabb oldal távolsága a kör középpontjától mostmár könnyen kiszámítható egy második derékszögű háromszögből: y2=r2-a2. Innen y=b2(1+1t2)-a2.
Mivel a körnek két olyan 2a hosszúságú húrja van, mely párhuzamos a 2b hosszúságú húrral, a középpont két oldalán, így a trapéz magasságára két lehetséges értéket kapunk: m1=x-y vagy m2=x+y.
Ismét az első megoldásban nyert eredményekhez jutottunk, de most az oldó képletből kapott megoldás két tagja geometriai értelmet nyert.
 

3. Egy számtani sorozat elemei egész számok, és egyik eleme négyzetszám. Bizonyítsuk be, hogy akkor bármeddig folytatva a sorozatot, elemei közt újra és újra fordulnak elő négyzetszámok.
 

I. megoldás. Legyen a2 a sorozatban előforduló négyzetszám és a sorozat szomszédos elemei közti különbség d. Ez nyilván szintén egész szám. Az a+kd alakú számok négyzete (k=0,1,2,...) mind elemei a sorozatnak. Valóban (a+kd)2=a2+(2ak+k2d)d és 2ak+k2d egész szám, így ez a négyzetszám eleme a sorozatnak (a2-től számítva a 2ak+k2d+1-edik eleme).
 

II. megoldás. Próbáljuk meg y-t úgy választani, hogy y2 eleme legyen a sorozatnak. Ez akkor áll fenn, ha y2 az a2-től d egész számú többszörösében különbözik. y2-a2=(y-a)(y+a) kell hogy osztható legyen d-vel. Ez bizonyosan fennáll, ha y=kd+a (k=0,1,2,...) vagy ha y=ld-a és l elég nagy egész szám. (Akkora, hogy (ld-a)2 ne legyen kisebb a sorozat legkisebb tagjánál.)
Ha d összetett szám, akkor ezenkívül további esetek is lehetségesek, melyben y-a és y+a oszthatók egy‐egy olyan számmal, amelyeknek szorzata adja meg d-t. Pl. a=2, d=21 mellett az y=21k+2, (k=0,1,2,...) és y=21 l-2 (l=1,2,3,...) alakú számokon kívül az y=21m+5 (m=0,1,2,...) és y=21n-5 (n=1,2,3,...) alakú számok négyzetei is elemei a sorozatnak. Az ilyen esetek teljes áttekintése is megadható, de már bonyodalmasabb volna.
1Beszorzással azonnal adódik az állítás helyessége n=1-re. Tegyük fel, hogy valamilyen n=k-1-re már igazoltuk az állítást.
Ekkor n=k-ra az
a2k+1+b2k+1a+b=a2a2k-1+b2k-1a+b-b2k-1a2-b2a+b=
=a2a2k-1+b2k-1a+b-b2k-1(a-b) azonosságból, beírva a tört helyébe feltevésünk szerint vele azonosnak bizonyult polinomot, adódik állításunk helyessége: n=k-ra is