Cím:	1950. évi Kürschák József matematikai tanulóverseny
Füzet:	1951/május, 2 - 11. oldal	PDF  |  MathML
Témakör(ök):	Kürschák József (korábban Eötvös Loránd)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Az 1950. évi Kürschák József matematikai tanulóverseny   A Bolyai János Matematikai Társulat 1950. október 14-én, rendezte meg a Kürschák József matematikai tanulóversenyt. A verseny Budapesten, Szegeden, Debrecenben, Miskolcon, Veszprémben, Pécsett és Egerben egyidőben folyt le. A versenyen 1950-ben érettségizettek és középiskolás diákok vehettek részt. A résztvevők és a beadott dolgozatok száma: Budapesten 208 versenyző, 77 dolgozat; Szegeden 32 versenyző, 7 dolgozat; Debrecenben 44 versenyző, 12 dolgozat; Miskolcon 21 versenyző, 8 dolgozat; Veszprémben 23 versenyző, 4 dolgozat; Pécsett 30 versenyző, 6 dolgozat, Egerben 20 versenyző, 2 dolgozat; összesen 378 versenyző és 116 dolgozat. A verseny feladatai a következők voltak: 1. Egy könyvtárban egy napon több olvasó fordul meg, s mindegyikük csak egyszer jár aznap a könyvtárban. Bármely három olvasó között van két olyan, aki a könyvtárban találkozik egymással. Bizonyítandó, hogy akkor meg lehet adni két időpillanatot úgy, hogy bármely olvasó a két időpillanatnak legalább egyikében a könyvtárban van. 2. A $k_1$, $k_2$ és $k_3$ kör három különböző pontban páronként érinti egymást. Összekötjük $k_1$ és $k_2$ érintési pontját a másik két érintési ponttal. Bizonyítandó, hogy ezek az összekötő egyenesek a $k_3$ kört egy átmérőjének, két végpontjában metszik. 3. $a_1$, $b_1$, $c_1$, $a_2$, $b_2$, $c_2$ olyan valós számok, hogy akármilyen $x$ és $y$ egészszámot helyettesítünk is az $\begin{array}{c}{\displaystyle a_{1}x+b_{1}y+c_1\text{<span style="font-weight: normal;font-style: normal;">és</span>}{a}_{2}x+b_{2}y+c_2}\end{array}$ kifejezésekbe, az eredmények között minden esetben van páros egészszám. Bizonyítandó, hogy akkor az $a_1$, $b_1$, $c_1$ és $a_2$, $b_2$, $c_2$ számhármasoknak legalább az egyike három egész számból áll.   A Bolyai János Matematikai Társulat elnöksége által kiküldött versenybizottság, melynek tagjai Gallai Tibor, Kárteszi Ferenc, Surányi János, Vincze István és Hajós György előadó, 1950 október 28-án tartott ülésén egyhangúan a következő jelentés fogadta el:   ,,Örvendetes tény, hogy a verseny résztvevőinek száma messze meghaladta a korábbi hasonló versenyekét. Ez részben annak köszönhető, hogy társulatunk a versenyt első ízben rendezte egyidejűleg hét helyen. A beadott dolgozatok viszonylagosan kevés helyes megoldást tartalmaznak. A harmadik feladatra egy versenyző sem adott be jó megoldást. Olyan dolgozat sincs, amelyik az első feladatot is és a másodikat is kifogástalanul oldja meg. A bizottság ezért úgy határozott, hogy az első Kürschák József-díjat ebben az évben nem adja ki.   A beadott dolgozatok közül kiemelkedik Bognár János és Szekerka Pál dolgozata. Bognár János a budapesti evangélikus gimnáziumban dr. Vermes Miklós tanár tanítványa volt és 1950-ben tett érettségi vizsgálatot. Beadott munkája az első feladatnak kifogástalanul megfogalmazott szabatos megoldását tartalmazza; a második feladatot megoldotta, bár a lehetséges esetek diszkutálásánál hibázott; a harmadik feladattal dolgozata nem foglalkozik. Szekerka Pál a budapesti VI. kerületi Rudas László gimnáziumban Neukomm Gyula tanár tanítványa és ez évben a II. osztályt végezte el. Dolgozatában helyes megoldását adja az első és második feladatnak, bár az utóbbinál csak egyféle elhelyezkedésre gondol; helyesen indul el a harmadik feladat megoldásánál is. A bizottság az 1950. évi második Kürschák József-díjat megosztva Bognár Jánosnak és Szekerka Pálnak itéli s munkájukat 300‐300 forinttal jutalmazza.   Megemlítendő még Korányi Ádám, Wellisch Tibor és Zergényi Erzsébet dolgozata. Mindhárman 1950-ben tettek érettségi vizsgálatot. Korányi Ádám azzal emelkedik ki, hogy valamennyi versenyző közül egyedül ő oldotta meg maradéktalanul a második feladatot, mert dolgozata minden lehetséges elhelyezkedésre kiterjed; az első feladatot lényegében megoldotta ugyan, de megoldásában több részlet kidolgozása hiányzik. Wellisch Tibor munkájának érdeme, hogy az első feladat helyes megoldásán kívül a harmadik feladattal is foglalkozik s annak megoldásában a versenyzők közül legmesszebbre jut; a második feladattal nem foglalkozik. Zergényi Erzsébet az első két feladatot oldotta meg, az elsőnek megoldását nem dolgozta ki s a másodiknál a lehetséges elhelyezkedéseket nem vizsgálta. A bizottság Korányi Ádám, Wellisch Tibor és Zergényi Erzsébet dolgozatát dicséretben részesíti.   Minthogy az első díjat a bizottság nem adta ki, lehetővé vált, hogy a dícséretben részesült munkák szerzői is pénzjutalmat kapjanak. A bizottság Wellisch Tibort és Zergényi Erzsébetet 100‐100 forinttal jutalmazza. Korányi Ádám az előző évi Kürschák József tanulóversenyen második díjat nyert s ezért a verseny szabályzata szerint dícséretben részesített dolgozatára pénzjutalmat nem kaphatott.''   1. feladat:   I. megoldás: Nézzük először azt az esetet, ha az olvasók közül bármelyik kettő találkozik a könyvtárban. Ekkor az utolsó érkezésétől az első távozásáig bármely időpontban az olvasók mindegyike a könyvtárban van. Ebben az esetben az először távozó olvasó is bevárja az utoljára érkezőt. Ha nem találkozik mindegyik mindegyikkel a könyvtárban, akkor válasszunk ki két olyan olvasót, akik nem találkoznak, legyenek ezek $a$ és $b$. A többi olvasót $3$ csoportra oszthatjuk. Az első csoportba tartoznak azok, akik találkoznak $a$-val, de $b$-vel nem. Ez legyen az $A$ csoport. A másodikba tartoznak azok, akik nem találkoznak $a$-val, csak $b$-vel. Ez legyen a $B$ csoport. A harmadikba azok tartoznak, akik mindkettővel találkoznak. Ez legyen a $C$ csoport. Minden könyvtárlátogató beletartozik e csoportok valamelyikébe, mert ha lenne olyan $c$ látogató, aki sem $a$-val sem $b$-vel nem találkozna, így $a$, $b$, $c$ nem találkoznak a könyvtárban, de ez a feltevés szerint nem fordul elő. Most $C$ azon egyedeit, kik $A$ minden egyedével találkoznak osszuk az $A$ csoportba, akik $B$ minden egyedével, azokat osszuk $B$-hez. Akik az $A$ csoportnak is, $B$ csoportnak is minden tagjával találkoznak, azokat bármelyikhez oszthatjuk. Az eredeti $A$ csoportban bármely látogatónak kellett találkoznia, mert ha ketten nem találkoztak volna, akkor ők $b$-vel oly hármast alkotnának, akik nem találkoznak a könyvtárban. A $C$ csoport tagjai szintén mind találkoznak egymással, hisz az $a$ eltávozása és $b$ megérkezése közötti időben mind bent kell hogy legyenek a könyvtárban. Viszont a $C$ csoport azon tagjai, akikkel az $A$ csoportot kibővítettük, mind találkoznak az $A$ csoport tagjaival, így a kibővített $A$ csoport minden tagja találkozik egymással, tehát van oly időpont, amint már láttuk; mikor mindnyájan a könyvtárban vannak. Ugyanígy látható be, hogy van egy oly időpont is, amikor a kibővített $B$ csoport tagjai mind a könyvtárban vannak. E két időpont olyan, hogy bármely egyén e két időpontnak legalább egyikében a könyvtárban tartózkodik. A $C$ csoport minden egyede találkozik vagy az $A$ vagy a $B$ csoport minden egyedével. Mert ha lenne a $C$ csoportnak egy olyan $c\text{'}$ egyede, aki az $A$ csoport egyik egyedével $a\text{'}$-vel és a $B$ csoport egyik egyedével $b\text{'}$-vel nem találkozna, akkor $a\text{'}$ sem találkozhatna $b\text{'}$-vel ‐ hiszen, mivel $c\text{'}$ nem találkozik sem $a\text{'}$-vel, sem $b\text{'}$-vel, $a\text{'}$ előbb menne el, mint $c\text{'}$ megérkezik, és $b\text{'}$ később érkezne meg, mint $c\text{'}$ elmenne ‐ így volna $3$ olyan egyed, ugyanis $a\text{'}$, $b\text{'}$, $c\text{'}$, akik egyáltalában nem találkoznának. 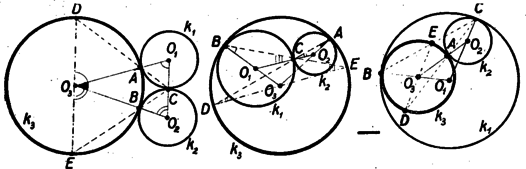  II. megoldás: Tekintsük azt a pillanatot, mikor az első olvasó eltávozik és azt a pillanatot, mikor az utolsó megérkezik. Ha valaki e két időpillanat egyikében sem volna ott, az csak úgy lehetne, ha az első eltávozása után érkezne ‐ hiszen előtte nem távozhat ‐ és az utolsó érkezése előtt távozna el ‐ hiszen utána nem érkezhet. Ez esetbén azonban ő, az első távozó és az utolsó érkező nem találkozna, ami ellentmond a feltevésnek.   III. megoldás: Képzeljük el a feladatot úgy, hogy a könyvtár portása utasítást kapott, hogy egy hirdetést olvasson fel két ízben, de úgy, hogy mégis minél többen hallják. Mikor válik szükségessé az első felolvasás? Nyilván akkor, amikor az első egyén távozni akar. És mikor kell másodszor felolvasni? Világos, hogy akkor, amikor azok közül, akik az első felolvasást nem hallották (tehát az első távozó után érkeztek) valaki távozni akar. Ha emellett teljesül a feladat kikötése is, akkor nem lehet, hogy valaki is ne hallotta volna a hirdetést, mert annak e két felolvasás után kellett volna jönnie, de ez esetben, ő, az első távozó, és az azután érkezők közül először távozó látogató közül senki senkivel sem találkozott volna.   Megjegyzés: E harmadik megoldás készen adja a feladat általánosításának bizonyítását is: ha $n$ tetszőleges pozitív egész szám és azt tesszük fel, hogy ($3$ helyett) bármely $n$ látogató közül találkozik legalább kettő a könyvtárban, akkor létezik olyan $n-1$ időpont, hogy minden látogató ezek valamelyikében a könyvtárban van.   2. feladat   E feladat megoldói közül egy kivételével, senki nem látta világosan, hogy három különböző esetet kell megvizsgálni: midőn a három kör kivülről érinti egymást, midőn $k_1$ és $k_2$ a $k_3$ kör belsejében van és midőn $k_3$ az egyik kört belülről, a másikat kívülről érinti. A továbbiakban hol egyik, hol másik, helyzetben tárgyaljuk a bizonyítást utalva a többi esetekben fellépő módosításra. Használni fogjuk a következő jelöléseket: a körök középpontja $O_1$, $O_2$, $O_3$; $k_2$ és $k_3$, $k_3$ és $k_1$, $k_1$ és $k_2$ érintési pontja rendre $A$, $B$, $C$, az $AC$ és $BC$ egyenesek a $k_3$ kört a $D$ és $E$ pontban metszik. (Ábra a köv. oldalon.)     I. megoldás: Vizsgáljunk kivülről érintkező köröket. Legyenek az $O_1{O}_2{O}_3$ háromszög szögei rendre $\alpha$, $\beta$ és $\gamma$. $A{O}_{2}C\Delta$ és $A{O}_{3}D\Delta$ egyenlőszárú és $A$-nál lévő szögeik egyenlők, mert csúcsszögek. Ha két egyenlőszárú háromszögben az alapnál fekvő egy-egy szög egyenlő, akkor az összes szögek egyenlők. Így $A{O}_{3}D\sphericalangle =A{O}_{2}C\sphericalangle =\beta$. Ugyanúgy következik a $B{O}_{1}C$ és $B{O}_{3}E$ egyenlőszárú háromszögekből, hogy $B{O}_{3}E\sphericalangle =\alpha$. Így a $D{O}_{3}E\sphericalangle$ egy $\alpha$, egy $\beta$ és egy $\gamma$ nagyságú szögből tevődik össze, tehát ${180}^{\circ }$-os, vagyis a $D$, $O_3$ és $E$ pont egy egyenesen, a $k_3$ kör egy átmérőjén fekszik. Ha a $k_3$ kör tartalmazza $k_1$-et és $k_2$-t, akkor a megoldásban szereplő háromszögpároknak az $A$ ill. $B$ csúcsnál fekvő szögei közösek és az $O_1$-nél $O_2$-nél illetve $O_3$-nál fekvő külső szögek egyenlőségét használva fel okoskodhatunk az előbbi módon. Ha $k_3$ a $k_1$ kör belsejében és a $k_2$ körön kívül van, akkor az első háromszögpárral az első esetnél, a másodikkal pedig a második esetnél elmondott módon okoskodunk és ismét arra az eredményre jutunk, hogy a $D{O}_3$ és $E{O}_3$ szárak között egy háromszög három szöge, vagyis éppen ${180}^{\circ }$ fekszik.   II. megoldás: Legyen $k_1$ és $k_2$ a $k_3$ kör belsejében. Elég megmutatnunk, hogy $D{O}_3\Vert E{O}_3$, mert a két egyenes egy pontja közös, tehát ez esetben egymás meghosszabbításába kell esniök. Ismét nézzük az $A{O}_{2}C$ és $A{O}_{3}D$ egyenlőszárú háromszögeket. $A$-nál levő szögük közös, tehát az alapon fekvő másik szögek is egyenlők: $AC{O}_2\sphericalangle =AD{O}_3\sphericalangle$. E szögek egy szára közös, s így megfelelő szögek, másik száruk is párhuzamos: $C{O}_2\Vert D{O}_3$. Ugyanígy kapjuk, hogy $C{O}_1\Vert E{O}_3$. De $O_1$, $C$ és $O_2$ egy egyenesen vannak, a két érintkező kör centrálisán, így $D{O}_3$ és $E{O}_3$ egymással is párhuzamosak, amiből következik a bizonyítandó állítás. Ha kívülről érintkező köröket vizsgálunk, akkor a háromszögpároknak egy-egy szöge csúcsszöget alkot, az alapjukon levő második szögek ez esetben váltószögek lesznek, tehát száraik ismét párhuzamosak. A harmadik esetben ismét az egyik háromszög párra úgy okoskodunk, mint az első, a másodikra úgy, mint a második esetben.   III. megoldás: Átfogalmazzuk a feladatot. Jelöljük $O$-val a három kör hatványpontját. (A közös érintők közös metszéspontját). Az $O$-ból a körökhöz húzott érintődarabok egyenlők $OA=OB=OC$. Így $O$ köré olyan $k$ kört lehet írni, mely átmegy az $A$, $B$, $C$ pontokon, és merőlegesen metszi mindhárom kört, mivel az érintő merőleges a sugárra. A feladat tehát helyettesíthető a következővel: az egymást merőlegesen metsző $k$ és $k_3$ körök $A$ és $B$ metszéspontját a $k$ kör tetszőleges $C$ pontjából vetítjük. Bizonyítandó, hogy az $AC$ és $BC$ egyenesek második metszéspontja $k_3$-mal, $D$ és $E$ átellenes pontok. Azt fogjuk megmutatni, hogy $D{O}_3$ és $E{O}_3$ ugyanarra az egyenesre merőleges. Ilyen egyenes $CO$. Tükrözzük ugyanis az ábrát egy $CD$-re merőleges $t$ tengely körül.     Ha egy kört egy húrjának felezőmerőlegesére tükrözünk, akkor a húr végpontjához húzott sugarak egymásba mennek át. Ha nem a felezőpontban húzzuk a merőleges tengelyt, ezek az egyenesek akkor is egymással párhuzamos helyzetekbe mennek át. Így a $k$ kört nézve $CO$ tükörképe $t$-re párhuzamos lesz $OA$-val. $k_3$-at nézve $O_{3}D$ képe párhuzamos lesz $O_{3}A$-val. De a két kör merőlegesen metszi egymást, ami azt jelenti, hogy a metszésponthoz húzott körsugarak merőlegesek egymásra: $OA\perp O_{3}A$. Ekkor azonban $OC\perp O_{3}D$ -re, mert a tükörképeik is merőlegesek egymásra. Ugyanígy következik egy $CE$ egyenesre merőleges tengelyre tükrözve, hogy $OC\perp O_{3}E$. Mivel az $O_{3}D$ és $O_{2}E$ egyenesek ugyanarra az egyenesre merőlegesek, így párhuzamosak egymással és miután az $O_3$ pontjuk közös, következik, hogy $D$, $O_3$ és $E$ egy egyenesen feküsznek, $k_3$ egy átmérőjén. Ennél az átfogalmazásnál a kezdetben említett három eset abban különbözik, hogy $C$ a $k$ kör különböző részeire esik, a bizonyítás azonban ettől függetlenül minden esetben érvényes. A feladat átfogalmazása egy általánosítást is kínál, melyet a $299$. feladatban tűzünk ki ($40$ old.).   IV. megoldás. A bizonyítandó állítás következik abból is, hogy ha megmutatjuk, hogy a $D$-ben és $E$-ben húzott érintők párhuzamosak. Nézzünk először két kört, $k$ és $k_3$ érintik egymást a $B$ pontban. Középpontjuk legyen $O$ és $O_3$. Egy $B$-n átmenő egyenes $k$-t $C$-ben, $k_3$-at $E$-ben metszi $OBC\sphericalangle =O_{3}BE\sphericalangle$. (Belülről érintkező köröknél egybeesik a két szög, külső érintkezésnél csúcsszögek). 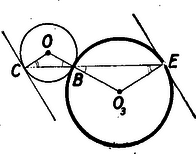    Mivel $BOC\Delta$ és $B{O}_{3}E\Delta$ egyenlőszárú, következik, hogy $OCB\sphericalangle =O_{3}EB\sphericalangle$. $B$, $C$ és $E$ egy egyenesbe esnek, így következik, hogy $OC\Vert O_{3}E$. (Belső érintkezésnél megfelelő szögek szárai, külső érintkezésnél váltószögekéi.) De ekkor a $C$-ben és $E$-ben húzott érintők, melyek ezekre a sugarakra merőlegesek, szintén párhuzámosak. Ezt a meggondolást a $k_2$ és $k_3$ körökre alkalmazva ugyanúgy következik, hogy a $C$-ben és $D$-ben húzott érintők is párhuzamosak. Még rövidebben mondhattuk volna el a bizonyítást, ha hivatkoztunk volna arra, hogy érintkező köröknek hasonlósági pontja az érintkezési pont, s azokban a pontokban, melyek ennél a hasonlóságnál egymásnak felelnek meg, az érintők párhuzamosak (Az előzőkben ennek az állításnak egy bizonyítását mondtuk el.) Hasonló tétel igaz térben is; érintkező gömbökre, érintők helyett érintő síkokkal, és felhasználható a feladat térbeli megfelelőjének bizonyítására, melyet a $305$. feladatban tűzünk ki ($41$. old.).   3. feladat.   A feladat megoldása tulajdonképpen nem kíván különösebb ötleteket, csak kitartóan végig kell próbálni az összes lehetőségeket. Hogy rövidebben fejezhessük ki magunkat, néhány rövid jelölést fogunk használni. Amit az együtthatókról tudunk, egy keretben fogjuk feltüntetni:     Ha egy együtthatóról azt tudjuk, hogy páros egészszám, akkor a helyébe egy $2$-est írunk, ha azt tudjuk, hogy páratlan egészszám, akkor $1$-est; ha pedig az derül ki, hogy két együttható összege páros egészszám, akkor ezek helyét egy $\circ -\circ$ jellel kötjük össze. Az üresen hagyott helyek azt jelentik, hogy a megfelelő együtthatókról még nem derült ki semmi. $\left(x\mathrm{,}y\right)=\left(a\mathrm{,}b\right)$-vel azt jelöljük, hogy $x$ helyébe $a$-t, $y$ helyébe $b$-t helyettesítünk.   I. megoldás: $1^{\circ }$. $\left(x\mathrm{,}y\right)=\left(\mathrm{0,0}\right)$ helyettesítéssel, azt kapjuk, hogy $c_1$ és $c_2$ közül valamelyik páros egészszám. Feltehetjük, hogy $c_1$ ez: $2^{\circ }$. Helyettesítsünk $\left(x\mathrm{,}y\right)=\left(\mathrm{1,0}\right)$-t. Ha $a_1+c_1$ páros, $a_1$ is páros, ha nem akkor $a_2+c_2$ páros:     $3^{\circ }$. $\left(x\mathrm{,}y\right)=\left(-\mathrm{1,0}\right)$ helyettesítésnél az első esetben biztos páros az első kifejezés, a másodikban mivel $-a_1+c_1$ nem lehet páros (akkor $a_1+c_1$ is az volna), tehát $-a_2+c_2$ kell, hogy páros legyen. Ez csak úgy lehet, ha vagy $a_2$ is $c_2$ is páros egészszám, vagy mindkettő páratlan:     $4^{\circ }$. $\left(x\mathrm{,}y\right)=\left(\mathrm{0,1}\right)$. Az első esetben, ha $b_1+c_1$ páros $b_1$ is az, ha nem akkor $b_2+c_2$ páros. A másodikban ha $b_1+c_1$ páros $b_1$ is az, ha nem akkor $b_2+c_2$ páros, de akkor $b_2$ páros egészszám kell legyen. A harmadikban ha $b_1+c_1$ páros, akkor $b_1$-nek páros egésznek kell lennie. Ha nem, akkor $b_2+c_2$ páros, de akkor $b_2$ páratlan egészszám:     Az $1$. és $4$. esetben bármely egész $\left(x\mathrm{,}y\right)$-ra az egyik kifejezés értéke páros lesz. Ezeket az eseteket nem is vizsgáljuk tovább. $5^{\circ }$. Legyen $\left(x\mathrm{,}y\right)=\left(\mathrm{0,}-1\right)$. $2$.-ben $-b_1+c_1$ nem lehet páros, mert akkor $b_1$ és $b_1+c_1$ is páros lenne. Így $-b_2+c_2$ páros, tehát vagy mindkettő páros egészszám, vagy mindkettő páratlan. Az első lehetőség csak a két kifejezés sorrendjében különbözik a $3$. esettől, így nem tárgyaljuk külön. $3$.-ban és $5$.-ben az első, $6$.-ban a második kifejezés biztosan páros:     $6^{\circ }$. Legyen $\left(x\mathrm{,}y\right)=\left(\mathrm{1,1}\right)$ $1$.-ben $a_1+b_1+c_1$ nem lehet páros, mert feltettük ($4$.-nél), hogy $b_1+c_1$ nem páros, tehát kell, hogy $a_2+b_2+c_2$ legyen páros. $b_2+c_2$ páros, így $a_2$ is páros. $2$.-ben hasonlóan kell, hogy $a_2+b_2+c_2$ legyen páros s így $b_2$ páros egészszám, amivel viszont lényegében a már elintézett esetre jutunk. $3$.-ban sem lehet $a_1+b_1+c_1$ páros, így $a_2+b_2+c_2$ az, amiből következik, hogy $b_2$ páros egésszám. $4$.-ben $a_2+b_2+c_2$ páratlan egészszám, tehát biztosan $a_1+b_1+c_1$ páros, tehát $a_1+b_1$ is páros. $a_1$-ről viszont $2$.-ben feltettük, hogy nem páros (t. i. azzal, hogy $a_1+c_1$ nem páros).     A bizonyítandó állítást ezzel már meg is kaptuk, hisz itt minden esetben a második kifejezés együtthatói egészszámok. A további helyettesítések csak a táblázatok teljes kitöltéséért történnek: $7^{\circ }$. Legyen $\left(x\mathrm{,}y\right)=\left(\mathrm{2,0}\right)$. $1$.-ben $2a_1+c_1$ biztos páros, így nem tudunk meg újabbat. $2$.-ben az első kifejezésnek kell párosnak lennie, tehát $2a_1+c_1$-nek, s így $2a_1$-nek is. $a_1$ tehát egész. Új eredményt csak akkor kapunk, ha $a_1$ páratlan. $3$.-ban szintén az első kifejezés s így $2a_1$ külön is páros, $a_1$ viszont nem az, így $a_1$ és vele együtt $b_1$ is páratlan egészszám:     $8^{\circ }$. Az első esetben $b_1$ megismerésére helyettesítsünk $\left(x\mathrm{,}y\right)=\left(\mathrm{0,2}\right)$-t. $2b_2+c_2$ páratlan, így $2b_1+c_1$, tehát $2b_1$ is páros, $b_1$ tehát egészszám. Ha páros, újat nem kapunk, tehát újabb lehetőség csak az, ha $b_1$ páratlan.   Így a következő öt eset lehetséges:     Az első kettőben csak a két elsőfokú kifejezés sorrendje, az utolsó kettőben pedig csak $x$ és $y$ szerepe van felcserélve. Így ezek nem lényegesen különböző esetek. Az első két esetben minden egész $x$, $y$ párra ugyanaz a kifejezés páros. A harmadikban, ha $x$ is $y$ is páros, vagy mindkettő páratlan, akkor az első, ha egyik páros, másik páratlan, akkor a második kifejezés lesz páros. A negyedik esetben páros $x$-re, az ötödikben páros $y$-ra az első kifejezés lesz páros, $y$ illetőleg $x$ párosságától függetlenül; páratlan $x$-re ill. $y$-ra viszont, a második. Ez a megoldás nehézségekbe nem ütközik, de fáradságos. Ilyenkor igyekszünk a próbálgatásokat lehetőleg ügyesen elrendezni, hogy kevés esetet szétválasztva gyorsan és áttekinthető módon juthassunk e] a kívánt eredményhez.   II. megoldás: Tekintsük az $\left(\mathrm{1,0}\right)$, $\left(\mathrm{0,0}\right)$ és $\left(-\mathrm{1,0}\right)$ helyettesítéseket. A három helyettesítés közül legalább valamelyik kettőre ugyanannak a kifejezésnek kell páros egészszámot adnia, mert összesen két kifejezésünk van. Bármelyik két helyettesítésre is lesz e kifejezés páros, biztos, hogy benne $a$ és $c$ egészszámok. Ugyanezzel az okoskodással adódik a $\left(\mathrm{0,1}\right)$, $\left(\mathrm{0,0}\right)$, $\left(\mathrm{0,}-1\right)$ helyettesítések segítségével, hogy valamelyik kifejezésben $b$ és $c$ egészszám. Ha mindkétszer ugyanarról a kifejezésről van szó, akkor $a$ is $b$ is $c$ is egészszám. Ha $a$ és $c$ az egyik kifejezésben bizonyul egésznek, $b$ és $c$ viszont a másikban, akkor $\left(\mathrm{1,1}\right)$ behelyettesítésével látjuk, hogy valamelyik kifejezésben $a+b+c$ is egész. Mivel két együtthatóról már tudjuk, hogy külön-külön egészszám, így következik, hogy a harmadiknak külön is egésznek kell lennie, így minden esetben valamelyik kifejezésben $a$ is $b$ is $c$ is, egészszám.   III. megoldás: Tekintsünk a számsíkon $5$ pontot: a $\left(\mathrm{0,1}\right)$, $\left(\mathrm{0,}-1\right)$, $\left(\mathrm{1,0}\right)$ $\left(-\mathrm{1,0}\right)$ és $\left(\mathrm{0,0}\right)$ pontokat. Ha $\left(x\mathrm{,}y\right)$ helyébe ezt az öt értéket helyettesítjük, valamelyik kifejezés mindegyik esetben páros egész értéket ad, így bizonyos, hogy az öt helyettesítés közül háromra ugyanaz a kifejezés lesz páros. Jelöljük együtthatóit index nélkül $a$, $b$, $c$-vel. Legyen a három helyettesítés $\left(x_1\mathrm{,}{y}_1\right)$, $\left(x_2\mathrm{,}{y}_2\right)$ és $\left(x_3\mathrm{,}{y}_3\right)$. Ez esetben $a{x}_1+b{y}_1+c=2A$, $a{x}_2+b{y}_2+c=2B$, $a{x}_3+b{y}_3+c=2C$, ahol $A$, $B$ és $C$ egészszámok. Szorozzuk meg az első egyenletet $\left(y_2-y_3\right)$-mal, a másodikat $\left(y_3-y_1\right)$-gyel, a harmadikat $\left(y_1-y_2\right)$-vel és adjuk őket össze. Ekkor $b$ és $c$ szorzója éppen $0$ lesz. A jobboldalon pedig újra páros szám keletkezik. Jelöljük $2D$-vel: $\begin{array}{c}{\displaystyle a\left[x_1\left(y_2-y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2\right)\right]=2D\mathrm{.}}\end{array}$ Ha a számpárokat pontok koordinátáinak fogjuk fel, akkor a szorzója éppen a három pont által alkotott háromszög kétszeres területe, ezt $2T$-vel jelölve, egyenletünk ilyen alakú lesz: $a\cdot 2T=2D$. A fenti egyenleteket sorra $\left(x_2-x_3\right)$-mal, $\left(x_3-x_1\right)$-gyel, $\left(x_1-x_2\right)$-vel szorozva és összeadva hasonlóan nyerjük, hogy $b\cdot 2T=2E$, ahol $E$ egészszám. Nézzük meg, most az öt számpárt ábrázoló pontokat. Ezek közül minden módon kiválasztva hármat vagy $1$, vagy $\frac{1}{2}$ területű háromszöget kapunk, vagy egy egyenesbe esik a három pont. Tehát $2T$ értéke $2$, $1$ vagy $0$. Első két esetben $a=\frac{2D}{2T}$ és $b=\frac{2E}{2T}$ s így velük együtt $c=2A-a{x}_1-b{y}_1$ is egészszámok. Ha a három pont egy egyenesre esik és a másik két pontnak megfelelő két helyettesítésre a másik kifejezés ad páros értéket, akkor végezzük el még az $\left(\mathrm{1,1}\right)$ helyettesítést. Ha erre ismét az első kifejezés lesz páros, akkor a most hozzávett pont és a $3$ egy egyenesen sorakozó pont közül a két szélső alkot egy $1$ területű háromszöget, ha pedig itt a második kifejezés értéke páros, akkor ez a pont és az ötből kimaradó két pont alkot egy ugyanilyen háromszöget. Ezek valamelyikével ismételhetjük tehát meg a fenti gondolatmenetet. Valamelyik kifejezésnek tehát mindegyik esetben mindhárom együtthatója egész.