Kezdőlap


Cím:	Egyenlőtlenségek (3.)
Szerző(k):	Aczél János , Surányi János
Füzet:	1951/november, 113 - 127. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

4. Függvények konvex voltának egyszerű algebrai feltételei

Előző közleményünkben láttuk, hogy bizonyos egyenlőtlenségek helyessége geometriailag nyilvánvaló abból, hogy valamely függvény görbéje (alulról nézve) konvex, ill. konkáv. Egyszerűbb függvényeknél ezt könnyű a függvény grafikus ábrázolása alapján megállapítani. Nézzük pl. a

\sqrt[]{x}

függvényt. Ennek csak pozitív

x

értékekre van értelme. Görbéje egy vízszintes tengelyű parabola felső fele, tehát (alulról) konkáv görbe. A

- \sqrt[]{x}

függvényt viszont ugyanennek a parabolának az alsó fele ábrázolja, tehát konvex görbe.
A

\sqrt[3]{x^{2}}

függvény ábrázolásánál a nagyon kis abszolút értékű számoknál kell sűrűn számítani függvényértéket, hogy kellően megbízható görbét rajzolhassunk. Ekkor azt vesszük észre, hogy az

x = 0

értékhez közeledve a görbe balról is, jobbról is hozzásimul az

Y

-tengely felső feléhez. Így a negatív

x

-ekre is konkáv a görbe, pozitív

x

-ekre is, de nem mondhatjuk azt, hogy az egész görbe konkáv, mert az

x = 0

helyen csúcsa van.
A

\sqrt[]{x^{3}}

függvénynek ismét csak pozitív

x

-ekre van értelme és ilyenekre domború görbe ábrázolja, mely az

Y

-tengely közelében hozzásimul az

X

-tengelyhez.
Az

\frac{1}{x}

görbe képe, mint tudjuk, egyenlőszárú hiperbola, melynek két ága nagy abszolút értékű

x

-ekre az

X

-tengelyhez simul; 0-hoz közeli negatív

x

-ekre az

Y

-tengely alsó, pozitívokra a felső feléhez simul. A negatív

x

-ekhez tartozó görbeág konkáv, a pozitív

x

-ekhez tartozó konvex.
Lényegében ugyanez a helyzet az

\frac{1}{x^{3}}

függvénnyel is, csak annyi a különbség, hogy annak a görbéje az

X

-tengelyhez sokkal gyorsabban közeledik, az

Y

-tengelyhez viszont sokkal lassabban, mint az

\frac{1}{x}

görbe. Ez azonban nem változtat azon, hogy a görbe domború, ill. homorú.
A

2^{x}

görbéje és

10^{x}

-é is negatív

x

-ekre az

X

-tengelyhez simul, 0-nál az értéke 1, pozitív

x

-ekre pedig egyre rohamosabban növekszik. A két függvénygörbe egészen hasonló menetű; csak a

10^{x}

mindenütt erősebben növekszik, mint a

2^{x}

. Hasonló a görbéje minden 1-nél nagyobb alapszám hatványait ábrázoló görbének is. Minél közelebb van az alapszám 1-hez, annál kevésbé meredeken fog emelkedni a függvény. Az 1 alapszámnak minden hatványa is, 1. Az

y = 1^{x} = 1

függvényt tehát egy vízszintes egyenes szemlélteti. Ha viszont az alapszám 1-nél kisebb pozitív szám, akkor a pozitív hatványai közelednek 0-hoz, negatív hatványai pedig minden határon túl nőnek, ha a kitevő abszolút értékét minden határon túl növeljük. A görbék most az 1-nél nagyobb alapokhoz tartozó görbék tükörképei az

Y

-tengelyre. Az összes ilyen görbék konvexek.
A lg

x

görbéje kis pozitív

x

-eknél nagy abszolút értékű negatív

y

értékektől meredeken emelkedik,

x = 1

-nél átmetszi az

X

tengelyt, azután egyre kevésbé meredeken emelkedik tovább. A görbe mindenütt konkáv.
A

sin x

és

cos x

függvényt hullámok ábrázolják. A hullámhegyek konkávok, a völgyek konvexek. Így az előbbi a

0 \leq x \leq π

, a

2 π \leq x \leq 3 π

, általában a

2 k π \leq x \leq (2 k + 1) π

intervallumokban konkáv, a

π \leq x \leq 2 π

3 π \leq x \leq 4 π

, általában a

(2 k + 1) π \leq x \leq (2 k + 2) π

intervallumokban konvex; utóbbi függvény pedig a

- \frac{π}{2} \leq x \leq \frac{π}{2}

\frac{3 π}{2} \leq x \leq \frac{5 π}{2}

és általában a

\frac{4 k - 1}{2} π \leq x \leq \frac{4 k + 1}{2} π

intervallumokban konkáv, a

\frac{π}{2} \leq x \leq \frac{3 π}{2}

\frac{5 π}{2} \leq x \leq \frac{7 π}{2}

és általában a

\frac{4 k + 1}{2} π \leq x \leq \frac{4 k + 3}{2} π

intervallumokban konvex (

k = 0

\pm 1

\pm 2

...

).
Különleges szerepe van domborúság szempontjából az

a x + b

alakú függvényeknek, hiszen ezeket egyenes ábrázolja, tehát se nem domborúak, se nem homorúak. Tágabb értelemben viszont konvexnek is, konkávnak is tekinthetjük ezeket. Más függvény nem is bírhat ezzel a tulajdonsággal, csak aminek egyenes a képe.¹
Írjuk fel pl. az

\frac{1}{x}

görbére, hogy minden olyan húr középpontja, melynek végpontjai pozitív abszcisszájúak, a görbe fölött van. Legyen

a

és

b

pozitív

\begin{matrix} \frac{\frac{1}{a} + \frac{1}{b}}{2} \geq \frac{1}{\frac{a + b}{2}}, azaz \frac{a + b}{2} \geq \frac{1}{\frac{\frac{1}{a} + \frac{1}{b}}{2}} = \frac{2 a b}{a + b} . \end{matrix}

A geometriai szemlélet tehát közvetlenül adta, hogy a számtani közép nagyobb a harmonikusnál. Sok egyéb érdekes és fontos egyenlőtlenséget írhatnánk még fel megállapításaink alapján, a baj csak az, hogy nem építünk biztos alapokra, mikor szemléletünkre bízzuk annak eldöntését, hogy egy függvény hol konvex, hol konkáv.
Eldönthetjük ezt a szemlélet igénybevétele nélkül is, éppen azt a tulajdonságot fejezve ki az algebra nyelvén, ami a konvex görbéket jellemzi, hogy a húr mindig a görbe fölött van. Legyen

x

az (

x_{1}, x_{2}

) szakasz egy belső pontja az

X

-tengelyen. Először is

x

-et szeretnénk

x_{1}

és

x_{2}

segítségével írni fel.

\begin{matrix} x = x_{1} + \frac{x - x_{1}}{x_{2} - x_{1}} (x_{2} - x_{1}) = \frac{x_{2} - x}{x_{2} - x_{1}} x_{1} + \frac{x - x_{1}}{x_{2} - x_{1}} x_{2} . \end{matrix}

x_{2} - x = p_{1}

x - x_{1} = p_{2}

jelölést használva

x_{2} - x_{1} = p_{1} + p_{2}

x

a távolságot

p_{2} : p_{1}

arányban osztó pont. Abszcisszájára:

\begin{matrix} x = \frac{p_{1} x_{1} + p_{2} x_{2}}{p_{1} + p_{2}} . \end{matrix}

x

az (

x_{1}, x_{1}

) szakasz belső pontja (és csakis ekkor)

p_{1}

és

p_{2}

pozitív. Ha

\frac{p_{1}}{p_{1} + p_{2}}

és

\frac{p_{2}}{p_{1} + p_{2}}

helyett

q_{1}

és

q_{2}

-t írunk, akkor

\begin{matrix} x = q_{1} x_{1} + q_{2} x_{2}, ahol q_{1}, q_{2} pozitív és q_{1} + q_{2} = 1. \end{matrix}

Írjuk fel most az

x_{1}

és

x_{2}

abszcisszájú pontok közti húr

x

abszcisszájú

B

pontjának ordinátáját. (Feltesszük a továbbiakban mindig, hogy

x_{1} \neq x_{2}

.) Jelöljük ezt

y

-na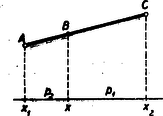l.

Az ábráról látható, hogy

\begin{matrix} \frac{y - f (x_{1})}{f (x_{2}) - y} = \frac{A B}{B C} = \frac{p_{2}}{p_{1}} = \frac{q_{2}}{q_{1}} . \end{matrix}

Innen egyszerű átalakítással nyerjük, hogy

\begin{matrix} y = \frac{p_{1} f (x_{1}) + p_{2} f (x_{2})}{p_{1} + p_{2}} = \frac{q_{1} f (x_{1}) + q_{2} f (x_{2})}{q_{1} + q_{2}} = q_{1} f (x_{1}) + q_{2} f (x_{2}) . \end{matrix}

A mondott geometriai tulajdonságot tehát így írhatjuk algebrai formában:

f (x)

akkor és csakis akkor konvex, ha minden

x_{1}

x_{2}

számhoz és bármely 0-tól különböző pozitív

p_{1}

és

p_{2}

számokra (úgynevezett súlyokra)

\begin{matrix} f (\frac{p_{1} x_{1} + p_{2} x_{2}}{p_{1} + p_{2}}) < \frac{p_{1} f (x_{1}) + p_{2} f (x_{2})}{p_{1} + p_{2}} . \end{matrix}

(1)

Írhatjuk az egyenlőtlenséget így is: bármely pozitív

q_{1}

és

q_{2}

súlyokra, melyekre

q_{1} + q_{2} = 1

\begin{matrix} f (q_{1} x_{1} + q_{2} x_{2}) < q_{1} f (x_{1}) + q_{2} f (x_{2}) . \end{matrix}

'

)

A nyert egyenlőtlenséget nevezik: súlyozott Jensen‐féle egyenlőtlenségnek. Ez fejezi ki tehát azt, hogy a függvény konvex. Ha

q_{1} = q_{2} = \frac{1}{2}

, akkor kapjuk a szimmetrikus Jensen-egyenlőtlenséget.

\begin{matrix} f (\frac{x_{1} + x_{2}}{2}) < \frac{f (x_{1}) + f (x_{2})}{2} . \end{matrix}

(2)

Pontosan ilyen számítással kapjuk, hogy egy

g (x)

függvény konkáv, ha bármely két pozitív

p_{1}

p_{2}

súlyra, ill. bármely két pozitív

q_{1}

q_{2}

súlyra, melyre

q_{1} + q_{2} = 1

\begin{matrix} g (\frac{p_{1} x_{1} + p_{2} x_{2}}{p_{1} + p_{2}}) > \frac{p_{1} g (x_{1}) + p_{2} g (x_{2})}{p_{1} + p_{2}}, \end{matrix}

ill.

\begin{matrix} g (q_{1} x_{1} + q_{2} x_{2}) > q_{1} g (x_{1}) + q_{2} g (x_{2}) . \end{matrix}

A tágabb értelemben konvex, ill. konkáv függvénynél az ívnek lehet közös pontja is a húrral, vagyis konvexre

\begin{matrix} f (q_{1} x_{1} + q_{2} x_{2}) \leq q_{1} f (x_{1}) + q_{2} f (x_{2}); \end{matrix}

konkávra

\begin{matrix} g (q_{1} x_{1} + q_{2} x_{2}) \geq q_{1} g (x_{1}) + q_{2} g (x_{2}) . \end{matrix}

Próbáljuk most ezen eredmény segítségével állapítani meg néhány függvényről, hogy konvex-e, vagy konkáv. Legyen pl.

f (x) = x^{2}

és képezzük erre az (

1'

) egyenlőtlenség két oldalának különbségét. Mivel

q_{1} + q_{2} = 1

\begin{matrix} q_{1} x_{1}^{2} + q_{2} x_{2}^{2} - {(q_{1} x_{1} + q_{2} x_{2})}^{2} = q_{1} (1 - q_{1}) x_{1}^{2} - 2 q_{1} q_{2} x_{1} x_{2} + \\ + q_{2} (1 - q_{2}) x_{2}^{2} = q_{1} q_{2} (x_{1}^{2} - 2 x_{1} x_{2} + x_{2}^{2}) = \\ = q_{1} q_{2} {(x_{1} - x_{2})}^{2} > 0, & (3) \end{matrix}

feltéve, hogy

q_{1} > 0

q_{2} > 0

és

x_{1} \neq x_{2}

. Az

x^{2}

függvényről tehát ezúton is megmutattuk, bogy konvex.
Vizsgáljuk most a

\sqrt[]{x}

függvényt. Alakítsuk át a

q_{1} \sqrt[]{x_{1}} + q_{2} \sqrt[]{x_{2}} - \sqrt[]{q_{1} x_{1} + q_{2} x_{2}}

kifejezést. Ezzel a gyökjelek miatt ebben az alakban nem tudunk mit kezdeni, de csökkenthetjük a kifejezésben a gyökjelek számát, ha szorzunk és osztunk

q_{1} \sqrt[]{x_{1}} + q \sqrt[]{x_{2}} + \sqrt[]{q_{1} x_{1} + q_{2} x_{2}}

-vel. (Részben gyöktelenítjük a kifejezést.) Ekkor a számláló így alakítható át:

\begin{matrix} (q_{1} \sqrt[]{x_{1}} + q_{2} \sqrt[]{x_{2}} - \sqrt[]{q_{1} x_{1} + q_{2} x_{2}}) (q_{1} \sqrt[]{x_{1}} + q_{2} \sqrt[]{x_{2}} + \sqrt[]{q_{1} x_{1} + q_{2} + x_{2}}) = \\ = {(q_{1} \sqrt[]{x_{1}} + q_{2} \sqrt[]{x_{2}})}^{2} - (q_{1} x_{1} + q_{2} x_{2}) = q_{1} (q_{1} - 1) x_{1} + \\ + 2 q_{1} q_{2} \sqrt[]{x_{1} x_{2}} + q_{2} (q_{2} - 1) x_{2} = - q_{1} q_{2} (x_{1} - 2 \sqrt[]{x_{1} x_{2}} + x_{2}) = \\ = - q_{1} q_{2} {(\sqrt[]{x_{1}} - \sqrt[]{x_{2}})}^{2} . \end{matrix}

Ez mindig negatív, a nevező viszont mindig pozitív, tehát a kifejezés most mindig negatív lesz. A függvény tehát konkáv.
Vizsgáljuk az

x^{3}

függvényt hasonló módon:

\begin{matrix} q_{1} x_{1}^{3} + q_{2} x_{2}^{3} - {(q_{1} x_{1} + q_{2} x_{2})}^{3} = q_{1} (1 - q_{1}) (1 + q_{1}) x_{1}^{3} - \\ - 3 q_{1}^{2} q_{2} x_{1}^{2} x_{2} - 3 q_{1} q_{2}^{2} x_{1} x_{2}^{2} + q_{2} (1 - q_{2}) (1 + q_{2}) x_{2}^{2} = \\ = q_{1} q_{2} [(2 q_{1} + q_{2}) x_{1}^{3} - 3 q_{1} x_{1}^{2} x_{2} - 3 q_{2} x_{1} x_{2}^{2} + (q_{1} + 2 q_{2}) x_{2}^{3}] = \\ = q_{1} q_{2} [q_{1} (2 x_{1}^{3} - 3 x_{1}^{2} x_{2} + x_{2}^{3}) + q_{2} (x_{1}^{3} - 3 x_{1} x_{2}^{2} + 2 x_{2}^{2})] . \end{matrix}

Erről már nem látszik olyan könnyen, hogy milyen az előjele. Vizsgáljuk az első zárójelben levő kifejezést és próbáljuk az első tagot egy teljes négyzet kifejezésbe foglalni, mely még

x_{1}

-gyel van szorozva. (Így tudjuk a harmadfokú tagot figyelembe venni.)

\begin{matrix} 2 x_{1}^{3} - 3 x_{1}^{2} x_{2} + x_{2}^{3} = 2 x_{1} (x_{1}^{2} - 2 x_{1} x_{2} + x_{2}^{2}) + x_{1}^{2} x_{2} - \\ - 2 x_{1} x_{2}^{2} + x_{2}^{3} = 2 x_{1} {(x_{1} - x_{2})}^{2} + x_{2} (x_{1}^{2} - 2 x_{1} x_{2} + x_{2}^{2}) = \\ = (2 x_{1} + x_{2}) {(x_{1} - x_{2})}^{2} . \end{matrix}

Hasonló érvényes a második kifejezésre is, csak ott

x_{1}

-et és

x_{2}

-t fel kell cserélni s így végül a fenti kifejezés így alakítható át:

\begin{matrix} q_{1} q_{2} {(x_{1} - x_{2})}^{2} [q_{1} (2 x_{1} + x_{2}) + q_{2} (x_{1} + 2 x_{2})] . \end{matrix}

Mivel

q_{1}

és

q_{2}

pozitív és

x_{1} \neq x_{2}

, ez biztosan pozitív, ha

x_{1}

és

x_{2}

pozitív, viszont biztosan negatív, ha

x_{1}

is,

x_{2}

is negatív. Az eredmény megegyezik azzal, amit az előző közleményben szemlélet alapján állapítottunk meg. A számolás kényelmetlenné válása viszont azt mutatja, hogy találtunk ugyan egy megbízható módszert a domborúság vizsgálására, de ez elég bonyolult módszer. Alkalmazzuk azért még egy egyszerű esetben: az

\frac{1}{x}

függvényre.

\begin{matrix} \frac{q_{1}}{x_{1}} + \frac{q_{2}}{x_{2}} - \frac{1}{q_{1} x_{1} + q_{2} x_{2}} = \frac{(q_{1} x_{2} + q_{2} x_{1}) (q_{1} x_{1} + q_{2} x_{2}) - x_{1} x_{2}}{x_{1} x_{2} (q_{1} x_{1} + q_{2} x_{2})} . \end{matrix}

Alakítsuk át a számlálót. Itt egy 1-es helyébe lesz célszerű majd

q_{1} + q_{2}

-t írni:

\begin{matrix} q_{1} q_{2} (x_{1}^{2} + x_{2}^{2}) + (q_{1}^{2} + q_{2}^{2} - 1) x_{1} x_{2} = q_{1} q_{2} (x_{1}^{2} + x_{2}^{2}) + \\ + [(q_{1}^{2} - q_{1}) + (q_{2}^{2} - q_{2})] x_{1} x_{2} = q_{1} q_{2} (x_{1}^{2} + x_{2}^{2}) - \\ - [q_{1} (1 - q_{1}) + q_{2} (1 - q_{2})] x_{1} x_{2} = q_{1} q_{2} (x_{1}^{2} - 2 x_{1} x_{2} + x_{2}^{2}) = \\ = q_{1} q_{2} {(x_{1} - x_{2})}^{2} . \end{matrix}

A számláló tehát ismét pozitív, a nevező biztosan pozitív, ha

x_{1}

és

x_{2}

is pozitív és biztosan negatív, ha

x_{1}

is,

x_{2}

is negatív. A függvény tehát pozitív értékekre konvex, negatív értékekre konkáv.⁴
Az utoljára nyert egyenlőtlenség szerint ha

x_{1}

x_{2}

q_{1}

q_{2}

pozitív,

x_{1} \neq x_{2}

és

q_{1} + q_{2} = 1

, akkor

\begin{matrix} \frac{q_{1}}{x_{1}} + \frac{q_{2}}{x_{2}} > \frac{1}{q_{1} x_{1} + q_{2} x_{2}} . \end{matrix}

Innen

\begin{matrix} q_{1} x_{1} + q_{2} x_{2} > \frac{1}{\frac{q_{1}}{x_{1}} + \frac{q_{2}}{x_{2}}} . \end{matrix}

Vagyis azt bizonyítottuk utolsó átalakításunkkal, hogy a súlyozott számtani közép nagyobb, mint a súlyozott harmonikus. A (3) egyenlőtlenségből viszont

\begin{matrix} q_{1} x_{1}^{2} + q_{2} x_{2}^{2} > {(q_{1} x_{1} + q_{2} x_{2})}^{2}, vagyis \sqrt[]{q_{1} x_{1}^{2} + q_{2} x_{2}^{2}} > q_{1} x_{1} + q_{2} x_{2}, \end{matrix}

azaz a súlyozott négyzetes közép viszont a számtaninál is nagyobb.

q_{1} = q_{2} = \frac{1}{2}

-et írunk, akkor a már ismerős

\begin{matrix} \sqrt[]{\frac{x_{1}^{2} + x_{2}^{2}}{2}} > \frac{x_{1} + x_{2}}{2} > \frac{2}{(\frac{1}{x_{1}} + \frac{1}{x_{2}})} = \frac{2 x_{1} x_{2}}{x_{1} + x_{2}} \end{matrix}

egyenlőtlenségekhez jutunk (feltéve, hogy

x_{1}

és

x_{2}

különböző pozitív számok).⁵
Használtuk a ,,súly'', ,,súlyozott'' elnevezést, és valóban a szereplő kifejezések a súlypont kifejezéséhez hasonlítanak. Helyezzünk az

X

-tengelyre az

x_{1}

pontban

p_{1}

súlyt, az

x_{2}

pontban

p_{2}

súlyt. Képzeljük ezeket súlytalan rúddal összekötve. A rúd súlypontja az elhelyezett súlyokkal fordított arányban osztja a rudat, vagyis abban az

x

pontban lesz, melyre

\frac{x - x_{1}}{x_{2} - x} = \frac{p_{2}}{p_{1}}

. Innen

\begin{matrix} x = \frac{p_{1} x_{1} + p_{2} x_{2}}{p_{1} + p_{2}} = q_{1} x_{1} + q_{2} x_{2}, ahol q_{1} = \frac{p_{1}}{p_{1} + p_{2}}, \\ q_{2} = \frac{p_{2}}{p_{1} + p_{2}}, q_{1} + q_{2} = 1. \end{matrix}

Ha viszont egy

f (x)

görbe

(x_{1}, y_{1}) = (x_{1}, f (x_{1}))

pontjában helyezünk el

p_{1}

súlyt, és az

(x_{2}, y_{2}) = (x_{2}, f (x_{1}))

pontban

p_{2}

súlyt, akkor hasonló számítást végezve az ordinátára is (és használva a fenti jelöléseket) az adódik, hogy a súlypont koordinátái

\begin{matrix} (q_{1} x_{1} + q_{2} x_{2}; \end{matrix}

A Jensen-egyenlőtlenség tehát azt fejezi ki, hogy ha egy konvex görbe két pontjára súlyokat helyezünk, akkor a súlyok súlypontja a görbe fölött van.⁶
Helyezzünk most több pontban súlyokat a görbére. Kössük össze a pontokat abban a sorrendben, ahogy a görbén következnek és az utolsót kössük össze az elsővel. Így konvex sokszög keletkezik. A fizikából tudjuk, hogy ha ennek csúcsaiba súlyokat teszünk, akkor a súlypont a sokszög belsejében lesz. Miután pedig a görbe, amibe a sokszöget írtuk, konvex (alulról), így ez esetben is a görbe fölött lesz a súlypont. Ezt szigorúan bebizonyíthatjuk már meglevő ismereteinkből.
Az (

x_{1}

y_{1}

), (

x_{2}

y_{2}

...

, (

x_{k}

y_{k}

) pontokban rendre elhelyezett

p_{1}

p_{2}

...

p_{k}

súlyok súlypontja a

\begin{matrix} (\frac{p_{1} x_{1} + p_{2} x_{2} + ... + p_{k} x_{k}}{p_{1} + p_{2} + ... + p_{k}}, \frac{p_{1} y_{1} + p_{2} y_{2} + ... + p_{k} y_{k}}{p_{1} + p_{2} + ... + p_{k}}) \end{matrix}

pont. Az állítást teljes indukcióval fogjuk igazolni.

k = 2

-re már láttuk az állítás helyességét. Tegyük fel, hogy

k = n - 1

-re már kiszámítottuk a súlypont koordinátáit

(n > 2)

n

darab pont súlypontjához úgy jutunk, hogy vesszük

n - 1

darab pont súlypontját, és ide képzeljük összpontosítva az

n - 1

darab pontba helyezett súlyokat. Ennek és az

n

-edik pontnak képezzük a súlypontját. Mivel feltevésünk szerint az

n - 1

pont súlypontjának pl. az abszcisszája

\frac{p_{1} x_{1} + p_{2} x_{2} + ... + p_{n - 1} x_{n - 1}}{p_{1} + p_{2} + ... + p_{n - 1}}

, a pontban elhelyezendő súly pedig

p_{1} + p_{2} + ... + p_{n - 1} = p

, így az

n

pont súlypontjának abszcisszája

\begin{matrix} \frac{p \frac{p_{1} x_{1} + p_{2} x_{2} + ... + p_{n - 1} x_{n - 1}}{p_{1} + p_{2} + ... + p_{n - 1}} + p_{n} x_{n}}{p + p_{n}} = \\ \frac{p_{1} x_{1} + p_{2} x_{2} + ... + p_{n - 1} x_{n - 1} + p_{n} x_{n}}{p_{1} + p_{2} + ... + p_{n - 1} + p_{n}} . \end{matrix}

Azt kaptuk tehát, hogy ha

n - 1

pontra helyes az állítás, akkor helyes

n

pontra is. Mivel 2-re már láttuk az állítás helyes voltát, ezzel megmutattuk, hogy általánosan érvényes. Az ordinátára szó szerint ugyanígy következik az állítás helyessége.

Az eredményben az egyes pontok koordinátáinak teljesen szimmetrikus a szerepe. Így nyilvánvaló, hogy ha más sorrendben vesszük a pontokat, akkor is ugyanehhez a súlyponthoz kell jutnunk. Még akkor is ugyanehhez a súlyponthoz jutunk, ha a súlyokat csoportokba foglaljuk és az egyes csoportok súlypontjaiból számítjuk az egész rendszer súlypontját. Az első

m

és következő

n

pont súlypontjának abszcisszája

\begin{matrix} ξ_{1} = \frac{p_{1} x_{1} + \dots + p_{m} x_{m}}{p + \dots + p_{m}} és ξ_{2} = \frac{p_{m + 1} x_{1} + \dots + p_{m + n} x_{m + n}}{p_{m + 1} + \dots + p_{m + n}} . \end{matrix}

Ide a megfelelő súlyok összegét helyezve kapjuk az egész rendszer súlypontjára, hogy

\begin{matrix} \frac{(p_{1} + ... + p_{m}) ξ_{1} + (p_{m + 1} + ... + p_{m + n}) ξ_{2}}{p_{1} + ... + p_{m} + p_{m + 1} + ... + p_{m + n}} = \\ = \frac{p_{1} x_{1} + ... + p_{m} x_{m} + p_{m + 1} x_{m + 1} + ... + p_{m + n} x_{m + n}}{p_{1} + ... + p_{m} + p_{m + 1} + ... + p_{m + n}}, \end{matrix}

és ugyanígy számolhatunk az ordinátákra is.

Helyezzünk most az

f (x)

görbe

x_{1}

x_{2}

...

x_{k}

abszcisszájú pontjaiba rendre

p_{1}

p_{2}

...

p_{k}

súlyokat. Megmutatjuk, hogy a görbe akkor és csakis akkor konvex, ha

\begin{matrix} f (\frac{p_{1} x_{1} + p_{2} x_{2} + ... + p_{k} x_{k}}{p_{1} + p_{2} + ... + p_{k}}) < \\ < \frac{p_{1} f (x_{1}) + p_{2} f (x_{2}) + ... + p_{k} f (x_{k})}{p_{1} + p_{2} + ... + p_{k}} . & (4) \end{matrix}

k = 2

-re az (1) egyenlőtlenség tartalmazza az állítást; nagyobb

k

-kra teljes indukcióval fogjuk bizonyítani.

Tegyük fel, hogy

k = n - 1

-re már igazoltuk az állítást

(n > 2) : f (x)

akkor és csakis akkor konvex, ha bármely

x_{1}

...

x_{n - 1}

-re

\begin{matrix} f (\frac{p_{1} x_{1} + ... + p_{n - 1} x_{n - 1}}{p_{1} + ... + p_{n - 1}}) < \frac{p_{1} f (x_{1}) + ... + p_{n - 1} f (x_{n - 1})}{p_{1} + ... + p_{n - 1}} . \end{matrix}

Ekkor ezen feltevés és (1) szerint, ha a függvény konvex, akkor

\begin{matrix} f (\frac{p_{1} x_{1} + ... + p_{n - 1} x_{n - 1} + p_{n} x_{n}}{p_{1} + ... + p_{n - 1} + p_{n}}) = \\ = f (\frac{(p_{1} + ... + p_{n - 1}) \frac{p_{1} x_{1} + ... + p_{n - 1} x_{n - 1}}{p_{1} + ... + p_{n - 1}} + p_{n} x_{n}}{(p_{1} + ... + p_{n - 1}) + p_{n}}) < \\ < \frac{(p_{1} + ... + p_{n - 1}) f (\frac{p_{1} x_{1} + ... + p_{n - 1} x_{n - 1}}{p_{1} + ... + p_{n - 1}}) + p_{n} f (x_{n})}{(p_{1} + ... + p_{n - 1}) + p_{n}} < \\ < \frac{(p_{1} + ... + p_{n - 1}) \frac{p_{1} f (x_{1}) + ... + p_{n - 1} f (x_{n - 1})}{p_{1} + ... + p_{n - 1}} + p_{n} f (x_{n})}{p_{1} + ... + p_{n - 1} + p_{n}} = \\ = \frac{p_{1} f (x_{1}) + ... + p_{n - 1} f (x_{n - 1}) + p_{n} f (x_{n})}{p_{1} + ... + p_{n - 1} + p_{n}} . \end{matrix}

Ebből következik, hogy állításunk minden

k

-ra helyes. Megfordítva ha a (4) egyenlőtlenség fennáll, akkor a függvény konvex, hiszen (

1'

) a (4) egyenlőtlenségnek speciális esete.
Itt is írhatunk

\frac{p_{1}}{p_{1} + ... + p_{k}}

\frac{p_{2}}{p_{1} + ... + p_{k}}

...

\frac{p_{k}}{p_{1} + ... + p_{k}}

helyett

q_{1}

q_{2}

...

q_{k}

-t. A

p

-kkel együtt ezek is pozitívok és

q_{1} + q_{2} + ... + q_{k} = 1

.
Ekkor a (4) egyenlőtlenség így is írható

\begin{matrix} f (q_{1} x_{1} + q_{2} x_{2} + ... + q_{k} x_{k}) < \\ < q_{1} f (x_{1}) + q_{2} f (x_{2}) + ... + q_{k} f (x_{k}) & (4') \end{matrix}

Ha speciálisan

q_{1} = q_{2} = ... = q_{k} = \frac{1}{k}

, akkor az

\begin{matrix} f (\frac{x_{1} + x_{2} + ... + x_{k}}{k}) < \frac{f (x_{1}) + f (x_{2}) + ... + f (x_{k})}{k} . \end{matrix}

Ha a függvény konvex, akkor ez is mindig teljesül.
A (4) és (

4'

) egyenlőtlenséget

k

-tagú súlyozott Jensen-egyenlőtlenségnek nevezzük. Az utolsó egyenlőtlenség a

k

-tagú szimmetrikus Jensen-egyenlőtlenség.⁷
Eredményünk alkalmas arra, hogy már bebizonyított egyenlőtlenségekből külön bizonyítás nélkül újabbakra következtessünk. Így ‐

k

tagra csak a szimmetrikus egyenlőtlenséget írva fel ‐ az

x^{2}

ill.

\frac{1}{x}

konvexitásából, amit az előzőkben bizonyítottunk, következik az

\begin{matrix} \frac{x_{1}^{2} + x_{2}^{2} + ... + x_{k}^{2}}{k} > {(\frac{x_{1} + x_{2} + ... + x_{k}}{k})}^{2}, \end{matrix}

és pozitív

x_{1}

x_{2}

...

x_{k}

értékekre az

\begin{matrix} \frac{\frac{1}{x_{1}} + \frac{1}{x_{2}} + \dots + \frac{1}{x_{k}}}{k} > \frac{1}{\frac{x_{1} + x_{2} + ... + x_{k}}{k}} \end{matrix}

egyenlőtlenségek helyessége is, amiket így is írhatunk:

\begin{matrix} \sqrt[]{\frac{x_{1}^{2} + x_{2}^{2} + ... + x_{k}^{2}}{k}} > \frac{x_{1} + x_{2} + ... + x_{k}}{k}, \end{matrix}

(5)

ha az

x

-ek közt van különböző. Ha pedig az

x

-ek még mind pozitívek is, akkor

\begin{matrix} \frac{x_{1} + x_{2} + ... + x_{k}}{k} > \frac{k}{\frac{1}{x_{1}} + \frac{1}{x_{2}} + \dots + \frac{1}{x_{k}}} . \end{matrix}

(6)

Tehát

k

szám négyzetes közepe nagyobb számtani közepüknél,

k

pozitív szám számtani közepe viszont nagyobb harmonikus közepüknél.
A tétel értékét különösen akkor fogjátok látni, ha megoldjátok a következő feladatot:

338. Bizonyítsuk be az (5) és (6) egyenlőtlenségeket a fenti általános tétel és teljes indukció felhasználása nélkül.

\begin{matrix} * \end{matrix}

A többtagú Jensen-egyenlőtlenség következik a kéttagúból és ezzel már egy olyan tétel birtokába jutottunk, amellyel bizonyos egyenlőtlenségekből újabb egyenlőtlenségek helyességére következtethetünk. Láttuk azonban azt is, hogy a kéttagú súlyozott Jensen-egyenlőtlenség teljesülését sem egész egyszerű igazolni még igen egyszerű függvényeknél sem. Nézzük meg, nem lehet-e erre is még egyszerűbb egyenlőtlenségekből következtetni. Szemléletesen világosnak látszik, hogy már akkor is biztosan következtethetünk egy függvénynek ‐ illetőleg a görbéjének a konvexségére, ha csak azt tudjuk, hogy minden húrfelező pontja (vagy általában egy pontja) a görbe íve fölött van. Mindig olyan görbére gondolunk, amelyik egy összefüggő vonallal megrajzolható. Az ilyen görbéket és a megfelelő függvényeket is röviden folytonosnak fogjuk nevezni. Ezeknek az egyik fontos tulajdonsága, hogy ha két folytonos görbe közül az egyik egy helyen a másik alatt van, egy másik helyen pedig fölötte, akkor e két hely közt valahol metszi egymást a két görbe (esetleg többször is, de legalább egyszer). Ezt a tényt a szemlélet alapján helyesnek fogadva el, ebből kiindulva már szigorú bizonyítását adhatjuk előbbi állításunknak konvex és folytonos függvényekre. Ha egy ilyen görbe egy íve valamely

a

helyen a húrja fölé jut, akkor megkeressük

a

előtt is, után is a legközelebbi helyet,

ξ_{1}

-et és

ξ_{2}

-t, ahol a görbe átmetszi a húrt. (Ezek megegyezhetnek esetleg

x_{1}

-gyel, ill.

x_{2}

-v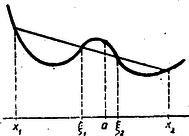el is.)

Ekkor

ξ_{1}

és

ξ_{2}

közt a görbe húrja teljesen a görbe alatt van. Ha tehát minden húr felezőpontja a görbe fölött van, akkor sehol sem kerülhet a görbe a húr fölé. De a húrra sem eshet, pontja a görbének, kivéve a húr végpontjait, mert ha volna más közös pont is, akkor elég kevéssel sülyesztve a húrt, már olyan húrt kapnánk, mely fölé emelkedik a görbe, de éppen most láttuk be, hogy ez lehetetlen, ha feltételünk teljesül. (Az ,,elég kevéssel süllyesztés'' pontosabban így értendő:

Ha a görbének a végpontok közt van még pontja a húron, akkor kiválasztva egy ilyen pontot; ez előtt is, utána is kiválasztható a konvexitás szerint, a görbének egy-egy pontja a húr alatt. Ha úgy húzunk az adott húrral párhuzamos egyenest az adott húr alatt, hogy a két kiválasztott pont fölött menjen el, akkor ez két-két olyan pont közt, melyek ennek a szelőnek ellenkező oldalán vannak, átmetszi a görbét, tehát valóban olyan húrt szolgáltat, melynek fölé emelkedik a görbe, s így alkalmazható rá az előbbi gondolatmenet.)

Ezzel igazoltuk is állításunkat. A hiba legfeljebb annyi, hogy ismét a szemléletre hivatkoztunk elég erősen, tehát ismét óvatosságra volna szükség, és meg kellene vizsgálni, hogy nem vezethet-e félre valami hamis látszat. Egy vonallal megrajzolható görbéről beszéltünk és rajzoltunk is ilyeneket. De vajjon nem rajzoshatók-e furcsább görbék is. Hiszen cikkünk elején is volt szó pl. olyan görbéről, aminek csúcsa van

(\sqrt[3]{x^{2}} -nek az x = 0 helyen)

. Valóban szigorú bizonyításhoz pontosabban meg kell mondani, hogy milyen függvényeket nevezünk folytonosnak, de a szigorúbb bizonyítás is történhetnék lényegében úgy, mint fönt elmondottuk. Ennek a részleteire nem térünk ki. Nézzük meg ellenben, hogy mit állíthatunk a folytonosság felhasználása nélkül.

339. Bizonyítsuk be, hogy ha egy függvény kielégíti a (2) kéttagú szimmetrikus Jensen-egyenlőtlenséget, akkor teljesül a négytagú, a nyolctagú, általában a

2^{j}

tagú szimmetrikus Jensen-egyenlőtlenség is (

j = 2

, 3, 4,

...

).
Tetszésszerinti

x_{1}

x_{2}

...

x_{n}

számokhoz határozzuk meg azt az

y

-t, amelyet még hozzávéve a számokhoz, az így kapott

n + 1

szám számtani közepe ugyanaz maradjon, ami az eredeti

n

számé volt. Bizonyítsuk be, hogy ha egy függvényre teljesül valamilyen tagszámú szimmetrikus Jensen-egyenlőtlenség, akkor teljesül minden kisebb tagszámú is.

A két eredmény együtt azt adja, hogy ha egy függvényre teljesül a kéttagú szimmetrikus Jensen-egyenlőtlenség, akkor teljesül bármilyen

k

-ra a

k

-tagú is. A feladatból adódó rendkívül szellemes és elegáns bizonyítás Cauchy (ejtsd: Kósi) múlt századbeli kiváló francia matematikustól ered. Az ő nevével gyakran fog találkozni, aki alaposabban meg akar ismerkedni a matematikával.
Ennek az eredménynek sok más bizonyítása is ismeretes. Még egyet feladunk, ami egy lépésben adja a bizonyítását.

340. Legyenek

x_{1}

x_{2}

...

x_{n}

x_{n + 1}

tetszésszerinti számok. Számítsuk ki azt az

y

-t, melyre igaz, hogy az első

n

adott szám számtani közepének és

y

-nak a számtani közepe ugyanaz, mint az adott

n + 1

szám számtani közepe.

Bizonyítsuk be, hogy ha egy függvényre teljesül a kéttagú szimmetrikus Jensen-egyenlőtlenség, akkor teljesül bármilyen

k

-ra a

k

-tagú is.
341. Bizonyítsuk be, hogy ha egy függvényre teljesül a kéttagú szimmetrikus Jensen-egyenlőtlenség, akkor teljesül a

k

-tagú súlyozott Jensen-egyenlőtlenség is, feltéve, hogy a súlyok racionális számok.

Azt gondolhatnánk, bogy most már befejezhető az okoskodás a folytonosság felhasználása nélkül, hiszen, ha a súlyok, vagy egy részük nem racionális számok, akkor is található hozzájuk akármilyen közel racionális szám is és ha ezzel helyettesítjük az irracionális súlyt, akkor tetszés szerint kevéssel változtatunk. De nem folytonos függvény változhatik nagyon sokkal is a változó igen kis változtatására (gondoljunk pl. az

\frac{1}{x}

függvényre az

x = 0

hely közelében). Így ennek a hátralévő lépésnek a megtételéhez fel kell használni a függvényről, hogy folytonos. Ennek a részleteire nem térünk ki.

Lássuk most eredményeink néhány alkalmazását (felhasználva azt a részben szemlélet alapján indokolt eredményünket is, hogy a függvény konvex volta már abból is következik, ha kielégíti a kéttagú szimmetrikus Jensen-egyenlőtlenséget).

342. Hol konvexek, hol konkávok a következő függvények:

10^{x}

lg x

a^{x}

{log}_{}^{⌣_{}^{a}} x

? Mutassuk meg, hogy az

x_{1}^{q_{1}} x_{2}^{q_{2}}

(q_{1} + q_{2} = 1)

súlyozott mértani közép az ugyanezen súlyokkal súlyozott számtani és harmonikus közép között van.

343. Mutassuk meg, hogy ha

h > - 1

, akkor

{(1 + h)}^{x} > 1 + h x

x > 1

és ha

x < 0

, viszont

{(1 + h)}^{x} < 1 + h x

, ha

0 < x < 1

. (Bernoulli‐egyenlőtlenség.)

344. Mutassuk meg, hogy ha

a

és

b

pozitív, akkor

\begin{matrix} a^{2} b \leq 4 {(\frac{a + b}{3})}^{3}; \end{matrix}

(7)

továbbá ha

r

és

s

olyan pozitív számok, melyekre

\frac{1}{r} + \frac{1}{s} = 1

, akkor

\begin{matrix} \frac{a^{r}}{r} + \frac{b^{s}}{s} \geq a b . \end{matrix}

(8)

345. Egyenlő területű derékszögű háromszögek közül melyiknek az átfogója a legkisebb? Hogyan lehet a feladatot ,,megfordítani'' (hasonlóan a 280., 282., 283. feladatokhoz)?

346. Hol konvex, hol konkáv a

sin x

és

cos x

függvény? (Használjuk fel a

sin α + sin β

, ill.

cos α + cos β

szorzat‐alakját.)

347. Bizonyítsuk be, hogy, ha

n

pozitív egész szám, akkor

\begin{matrix} \frac{{({x_{1}}^{n} + {x_{2}}^{n})}^{n + 1}}{{({x_{1}}^{n - 1} + {x_{2}}^{n - 1})}^{n}} \leq \frac{{({x_{1}}^{n + 1} + {x_{2}}^{n + 1})}^{n}}{{({x_{1}}^{n} + {x_{2}}^{n})}^{n - 1}} . \end{matrix}

A (közönséges)

n

-edik hatványközépen értjük az

\sqrt[n]{\frac{{x_{1}}^{n} + {x_{2}}^{n}}{2}}

értéket. Mutassuk meg, bogy az

n

-edik hatványközép kisebb az

n + 1

-ediknél. Mutassuk meg ugyanezt a súlyozott hatványközepekre is (a gyök alatt a hatványok számtani közepe helyett súlyozott számtani közepet véve).

348. Legyen

r

racionális szám.⁸ Mutassuk meg, hogy

y = x^{r}

konvex, ha

r

egynél nagyobb, vagy pedig negatív; konkáv, ha

0 < r < 1

.
Mutassuk meg, hogy az

r

-edik hatványközép nő, ha

r

nő. A mértani közép az

r

-edik és

- r

-edik hatványközép közé esik.

349. Az

a^{x}

és

{log}_{}^{⌣_{}^{a}} x

x^{n}

és

\sqrt[n]{x}

1 / x^{n}

és

1 / \sqrt[n]{x}

függvénypárok közt rokonság van. Miben áll ez a rokonság? Az ilyen függvényeket egymás inverzeinek nevezzük. Miért különleges ebből a szempontból az

1 / x

függvény? Tudunk-e más ilyen függvényeket is mondani? (,,involutórius függvények''). Konvex függvény inverze mikor konvex, mikor konkáv?

350. Mutassuk meg, hogy az

a^{x^{2}}

függvény konvex, felhasználva, hogy

a^{x}

és

x^{2}

konvex függvények. Azt mondjuk, hogy egy

h (x)

függvény az

f (x)

és

g (x)

függvények összetétele, ha a

h

függvény értékeit megkaphatjuk úgy, hogy az

f

függvény értékeit számítjuk ki, de nem az

x

helyen, hanem mindig arra az értékre, amelyet a

g

függvény vesz fel az

x

helyen, tehát

h (x) = f (g (x))

. Természetesen az

f

és

g

sorrendje lényeges. Röviden azt is mondjuk, hogy

h (x)

g

függvény

f

függvénye. Bizonyítsuk be, hogy ha egy függvény egy konvex függvénynek konvex és növekedő függvénye, akkor maga is konvex függvény.

¹Ezzel a 311. feladatnak adtuk megoldását.

²Ezzelmegoldásátadtuka312.feladatnak.

³Ezzelmegoldásátadtuka313.feladatnak.

⁴Ezzel megoldását adtuk a 314. feladatnak.

⁵ Ezzel megoldását adtuk a 315. feladatnak.

⁶Ezzel megoldását adtuk a 316. feladatnak.

⁷Ezzel megoldását adtuk a 317. feladatnak

⁸Irracionális $r$ -ekre is igazak állításaink, csak azt nehezebb bizonyítani. Erre nem fogunk kitérni.