Cím: Egyenlőtlenségek (2.)
Szerző(k):  Aczél János ,  Surányi János 
Füzet: 1951/augusztus, 62 - 71. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek
Hivatkozás(ok):Feladatok: 1951/május: 285. matematika feladat, 1951/május: 286. matematika feladat, 1951/május: 287. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

2. Egyenlőtlenségek átalakítása
 

Mielőtt egyenlőtlenségekkel foglalkoznánk, először tisztáznunk kell, hogyan lehet egyenlőtlenségeket átalakítani, belőlük újabb helyes egyenlőtlenségeket nyerni. Legyen A és B két valós szám. A>B ugyanazt jelenti, mint hogy az A-B különbség pozitív. (Jelben így is írhatjuk: A-B>0). Az első közleményben a két szám számtani és mértani közepe közt fennálló egyenlőtlenséget is úgy sikerült bizonyítani, hogy különbségük előjelét állapítottuk meg. Hasonlóan bizonyíthatunk más egyenlőtlenségeket is.
Tegyük fel, hogy
A>B,
(azaz, hogy A-B pozitív).
a) Ekkor (A+C)-(B+C)=A-B is pozitív, tehát
A+C>B+C.

b) Másrészt cA-cB=c(A-B) pozitív, ha c pozitív, de negatív, ha c negatív, tehát
ha c pozitív, cA>cB;  ha c negatív  cA<cB.
c) Vizsgáljuk most A és B hatványait. A2-B2=(A-B)(A+B), A3-B3=(A-B)(A2+AB+B2) és általában bármely pozitív egész n-re An-Bn=(A-B)⋅(An-1+An-2B+...+ABn-2+Bn-1). Az első tényező feltétel szerint mindig pozitív. A második tényező előjeléről biztosat tudunk mondani, ha A is, B is pozitív. Ekkor biztos, hogy a második tényező és vele együtt a szorzat is pozitív, tehát ha A>B és A is B is pozitív, akkor A2>B2, A3>B3, általában An>Bn (n=2,3,4,...).
d) Mit tudunk mondani A és B reciprokáról?
1A-1B=B-AAB=-A-BAB.
Ha ismét A is B is pozitív, akkor a nevező is pozitív, feltevés szerint a számláló is pozitív, így a tört negatív az előtte álló előjel miatt, tehát
1A<1B.

Általában 1An-1Bn=Bn-AnAnBn. Ha n pozitív egész és A is B is pozitív számok, akkor a nevező pozitív, a számláló viszont a föntebb végzett átalakítások szerint negatív, így a tört értéke is, tehát
1An<1Bn(n=1,2,3,...).
(Ez a c) pont alapján következik az éppen bebizonyított 1B>1A egyenlőtlenségből is.)
e) Legyen most A>B és C>D, vagyis A-B is, C-D is pozitív. Ekkor mindig pozitív A+C-(B+D)=(A-B)+(C-D) is, tehát
A+C>B+D.

f) Próbáljuk meg AC-BD-t is A-B és C-D segítségével kifejezni. E különbségeket rövidebb írás kedvéért b-vel és d-vel jelölve A=b+B, C=d+D. Így AC-BD=(b+B)(d+D)-BD=bd+bD+Bd (b és d jelentését beírva könnyen látható az azonosság helyessége). Ha itt B is D is pozitív, akkor az utolsó kifejezés is, tehát AC-BD is. A feltételből természetesen az is következik, hogy a B-nél nagyobb A is és a D-nél nagyobb C is pozitív, tehát ha A<B, C<D és A, B, C, D pozitív számok akkor
AC>BD.

Ezt az egyenlőtlenséget bebizonyíthattuk volna már előbb helyesnek bizonyult átalakítások segítségével is. Ugyanis b) szerint ha A>B és C pozitív, akkor AC>BC. Hasonlóan, ha C>D és B pozitív, akkor BC>BD is fennáll.
Viszont általában ha α, β, és γ három olyan szám, amelyekre
α>βésβ>γakkorα>γ
is fennáll, mert α-γ=(α-β)+(β-γ) és a jobboldalon mindkét kifejezés feltétel szerint pozitív.
Így az előbb nyert egyenlőtlenségekből következik a bizonyítandó AC>BD egyenlőtlenség. 1
Itt az egyenlőtlenségekben szereplő mennyiségekre bizonyos feltételeknek kell teljesülniök, hogy az egyes következtetéseket levonhassuk. Kérdés azonban, hogy nem teljesül-e valamelyik egyenlőtlenség akkor is mindig, ha a feltételek valamelyikét elhagyjuk? Figyeljük meg pl. az f) esetre adott kétféle bizonyítást. Az elsőből szükségesnek látszott B-ről is, D-ről is feltenni, hogy pozitívok. A második bizonyításban viszont csak annyit használtunk fel, hogy B és C pozitív. Az előbbivel együtt pozitívnak kell lennie A-nak is, de D előjelére nem következik ebből semmi és valóban igaz is, hogy az AC>BD egyenlőtlenség helyes akkor is, ha a kiinduló egyenlőtlenségeken kívül csak A, B és C-ről tudjuk, hogy pozitív, D azonban negatív.
Ennél többet azonban nem lazíthatunk a feltételeken. Ha pl. a két jobboldal negatív, akkor a 2>-3, 4>-2 egyenlőtlenségpár jobb- és baloldalainak szorzata közt a 8=2⋅4>(-3)(-2)=6 egyenlőtlenség áll fenn, viszont a 2>-3, 4>-3 egyenlőtlenségpár jobb- és baloldalainak szorzata közt a 8=2⋅4<(-3)(-3)=9 egyenlőtlenség. Így, ha mindkét jobboldal negatív, akkor azt sem állíthatjuk, hogy mindig a baloldalak szorzata a nagyobb, de azt sem, hogy mindig a jobboldalaké, mert mindkét esetben van olyan ,,ellenpéldánk'', amiben nem ez az eset következik be.
Mivel -1>-2, 3>2-ből -3=(-1)⋅3>(-2)2=-4, de viszont -1>-2, 5>2-ből -5=(-1)⋅5<(-2)⋅2=-4, tehát akkor sem vonhatunk általános következtetéseket, ha az egyik egyenlőtlenség mindkét oldala negatív.
Ha a két egyenlőtlenség három tagja negatív, akkor a b) értelmében -1-gyel szorozva az egyenlőtlenségeket és az egyenlőtlenségjeleket az ellenkező értelművel cserélve fel, a már bebizonyított esetekre jutunk. Alkalmazásban azonban legtöbbször csak az f) alatt kimondott esetre lesz szükségünk.
A c) pontban ha A pozitív, B negatív, akkor semmit sem mondhatunk, mert pl. 3>-2, 3>-3, 3>-4. Az első esetben 32>(-2)2, a másodikban 32=(-3)2, a harmadikban 32<(-4)2.
Ha A is, B is negatív, akkor A>B-ből a b) pont szerint -A<-B, vagy -B>-A következik s így a c) pont szerint (-B)n>(-A)n. Ebből, ha n páros, azt kapjuk, hogy Bn>An, ha n páratlan, akkor viszont -Bn>-An, An>Bn, tehát egyrészt a c) pontban szereplő egyenlőtlenségre egész általánosan csak pozitív A és B mellett következtethetünk, másrészt a további eseteket erre vissza tudjuk vezetni. Teljesen hasonló a helyzet A és B előjelével a d) pontban is.
A másik feltevés a c) és d) pontban az, hogy az n hatványkitevő pozitív egész szám. A következtetés azonban helyes marad, minden pozitív (nem egész) n kitevőre is. Ha n=1/q, q pozitív egész, A és B pozitív és A>B, akkor nem lehet 2 A1q=B1q(A1q=B1q), mert ekkor A=B volna. Ha A1q<B1q állna fenn, akkor q-adik hatványra emelve a c) pont szerint következnék, hogy A<B, tehát csak az lehet, hogy A1q>B1q. Ebből c) szerint az is következik, hogy ha p pozitív egész szám, akkor
ApqP>Bpq

Rajzoljuk most meg az y=Ax és y=Bx 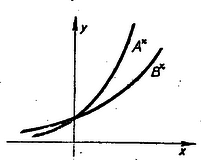görbét.
 
 

Minden tört számmal fel nem írható x-hez akármilyen közel találunk tört számot. Ezekben mindig az első görbe van magasabban, mint a második, a görbék pedig összefüggő vonallal rajzolhatók meg, így az x pontban is az első görbe lesz magasabban.
Teljesen hasonlóan okoskodhatunk a d pontban is. 3
Az e) és f) pontban azt is felvethetnénk, hogy hogyan változik a helyzet, ha az egyik egyenlőtlenség helyett a két mennyiség egyenlőségét tudjuk. Legyen most pl. A<B és C=D, akkor mivel B>A és BC=BD az a) pont szerint BD=BC>AC, vagyis AC<BD. Ha pedig A (és vele együtt B is) pozitív, akkor a b) pont szerint AC<BD áll fenn. 4
Miután két mennyiség A és B közt három kapcsolat állhat, fenn: A>B vagy A=B vagy A<B, így gyakran előfordul, hogy ezek közül csak az egyiket akarjuk kizárni. Az A≠B jelöléssel már ebben a cikkben is találkoztatok. A többi esetben a fennmaradó két lehetőséget szoktuk felírni jelben. Például azt, hogy A nem lehet kisebb B-nél, így írjuk: A≥B, és úgy olvassuk: ,,A nagyobb B-nél, vagy egyenlő vele''. Akkor az f) alatti és a most nyert eredményt (abban A-t és B-t felcserélve) így egyesíthetjük: ha
A>BésC≥DésA,B,C,Dpozitív,
akkor
AC>BD.
Ugyanezen feltétel mellett
A+C>B+D.
Azt figyeljük meg, hogy ha csak az egyik feltételben is nem szerepel az egyenlőségjel, akkor már a következményben sem állhat egyenlőség. Ha az első egyenlőtlenség helyett is A≥B állna, akkor már a következményben is ≥-t kellene írnunk, de még mindig azzal a megszorítással, hogy a következményben csak akkor áll fenn egyenlőség, ha mind a két feltételben az egyenlőség áll fenn.
 

3. Konvex függvények.
 

Első közleményünkben bebizonyítottunk egy egyenlőtlenséget a számtani és mértani közép között és alkalmaztuk geometriai szélsőértékfeladatok megoldásában. A 252. feladat II. megoldásában (75‐76. old.) egy másik egyenlőtlenséget használtuk geometriai szélsőértékfeladat megoldásában. Ezt az egyenlőtlenséget következő alakjában bizonyítottuk be: ha a,b pozitív számok, akkor a számtani közép négyzete és az ú. n. négyzetes közép közt a következő egyenlőtlenség áll fenn: 5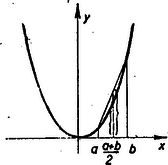
(a+b2)2≤a2+b22.
Ezt felfoghatjuk úgy, hogy az y=x2 függvényt ábrázoló görbe egy tulajdonságát fejezi ki. Rajzoljuk fel a görbét és az a és b abszcisszájú pontokat. Ezek ordinátái a2 és b2. Így a2+b22 az e két pontot összekötő húr felezőpontjának az ordinátája. E pont abszcisszája a+b2 így (a+b2)2 a görbe ugyanilyen abszcisszájú pontjának az ordinátája. Az egyenlőtlenség tehát azt fejezi ki, hogy a görbe bármely húrjának a felezőpontja a görbe fölött van. Ez szemléletesen világos is, mert a görbe alulról nézve domború, vagy idegen szóval konvex, s így egy húr minden pontja a görbe fölött van.
 
 

Ezek szerint hasonló egyenlőtlenséget nyerhetünk, ha ábrázolunk függvényeket és megnézzük, hogy az őket ábrázoló görbék alulról nézve domborúak-e vagy sem. Ezt ránézésre is könnyen eldönthetjük, ha a görbe elég egyszerű. Legfeljebb akkor merül fel kétség, ha a görbe ilyen alakú: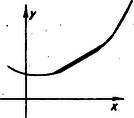
 
 


tehát egy darabja nem is homorú, nem is domború, hanem egyenes. Az ilyen görbéket is nevezhetjük konvexnek (alulról) akkor a konvexség tágabb értelmezéséhez jutunk. Egyezzünk meg abban, hogy a jövőben ha görbék domborúságáról beszélünk, azt mindig alulról nézve gondoljuk. Továbbá, ha röviden konvexet (domborút) mondunk, akkor mindig a szűkebb értelemre gondolunk tehát olyan görbére, amelyben nincs egyenes rész. Ellenkező esetben mindig jelezni fogjuk, hogy tágabb értelemben konvex görbéről van szó.
Ha egy függvényt konvex görbe ábrázol, akkor a rövidség kedvéért a függvényt is konvexnek nevezzük. Hasonlóan, ha egy függvény görbéje alulról homorú (konkáv), akkor a függvényt is konkávnak nevezzük. Ha a görbe konvex, ill. konkáv, de előfordulhat benne egyenes rész is, akkor tágabb értelemben konvexnek, ill. tágabb értelemben konkávnak nevezzük és ugyanígy a függvényt is, amelyet ábrázol.
Aki már ábrázolta az x3 függvényt, emlékszik rá, hogy ennek a görbének az y tengelytől jobbra eső darabja alulról domború, az y tengelytől balra eső része viszont alulról homorú.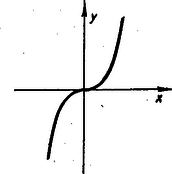
 
 

Ilyenkor a függvényről is azt mondjuk, hogy a megfelelő szakaszon konvex, ill. konkáv; tehát pl. az x3 függvény x pozitív értékeire konvex, negatív értékeire pedig konkáv.
 

311. Ábrázoljuk a
x,-x,x213,1x,1x3,2x,10x,lgx(=logx⌣10),(A)ax(a  tetszőleges pozitív szám),sinx,cosx,ax+b


függvényeket és állapítsuk meg a rajz alapján, hogy x mely értékeire konvexek, mely értékeire konkávok ezek a függvények. Milyen különleges tulajdonsága van ezek közül az utolsó kifejezéssel jellemezhető függvényeknek konvexség szempontjából? Van-e más hasonló tulajdonságú függvény is?
 

*
 

Nem nagyon megbízható dolog azonban egy függvény tulajdonságait az őt ábrázoló görbéről olvasni le, mert ezt a görbét nem tudjuk pontosan megrajzolni. Csak egyes pontokban számíthatjuk ki a függvényértéket és azoknak az ábrázolásánál is követhetünk el hibát, de különösen az függ egyéni megítélésünktől, és kézügyességünktől, hogy hogyan húzzuk a görbét a kijelölt pontok között. Az ábra magában például már arra sem volna teljesen megbízható, hogy megkeressük az x3 függvénynél azt a pontot, ahol a görbe (alulról nézve) konvexből átfordul konkávba. Mikor mégis természetesnek vesszük, hogy ez a pont a 0, akkor beleszámítjuk azt is, hogy a 0 pontnak bizonyos központi helyzete van ennél a görbénél. Valóban minden x értékre (-x)3=-x3. Ez geometriailag azt jelenti, hogy a görbe x és -x abszcisszájú pontjai egymás tükörképei a 0 pontra nézve. A 0 pontnak ezt a tulajdonságát azonban nem a grafikonról könnyű leolvasni, hanem a függvény matematikai kifejezéséből. Ha megpróbáljátok az xx2+1 görbét ábrázolni, az a 0 helyen átmegy domborúból homorúba, de ezen kívül negatív x-ekre is, pozitívokra is egy helyen átfordul homorúból domborúba. Ezeknek a fordulópontoknak a helyét már nehéz volna rajzról kielégítő pontossággal leolvasni, mert a közelükben nagyon kevéssé görbül a görbe. Az is előfordulhat, hogy a görbe oly kis darabon hajlik át homorúból domborúba és vissza, hogy azt rajzolás közben észre sem vesszük.
Szükségünk van tehát a grafikus ábrázolásnál biztosabb eszközre ahhoz, hogy eldöntsük egy függvényről, hogy konvex-e egy darabon vagy sem. Az erre kínálkozó út az, hogy keresünk olyan geometriai tulajdonságokat, amik teljesen kifejezik azt, hogy a görbe konvex, de emellett arra is alkalmasak, hogy ábrázolás nélkül, kizárólag a függvénnyel felírhatók legyenek. Sok ilyen tulajdonság van. Ezek közt az egyik legegyszerűbbet már meg is fogalmaztuk éppen akkor, amikor egyenlőtlenségek és a függvénygörbe domborúsága közt találtunk kapcsolatot: (alulról) domború görbének egy, húr végpontjai közti íve teljesen a húr alatt van. Megfordítva is: ha egy görbedarabnak bármely húrja a megfelelő ív felett van, akkor a görbedarab konvex.
Próbáljuk meg ezt a geometriai tulajdonságot a függvény segítségével felírni.
 

312. Legyen az X tengely két adott pontjának koordinátája x1 és x2. Mutassuk meg, hogy bármely köztük levő pont alkalmas pozitív p1 és p2 számokkal felírható
p1x1+p2x2p1+p2(B)
alakban. Áttekinthetőbbé válik a kifejezés, ha p1p1+p2-t q1-gyel p2p1+p2-t q2 vel jelöljük. Ekkor a pont így is írható:
q1x1+q2x2(B')
ahol q1 és q2 pozitív és q1+q2=1.
Hogyan írható fel egy f(x) függvény görbéjének x1 és x2 abszcisszájú pontjai közötti húrján (B) ill. (B') abszcisszájú pont ordinátája?
Írjuk le a konvexséget kifejező fenti tulajdonságot a függvényre vonatkozó egyenlőtlenség alakjában.
A nyerendő egyenlőtlenséget nevezik Jensen-egyenlőtlenségnek. Ha ebben q1=q2(=12) ill. p1=p2, akkor kapjuk a szimmetrikus Jensen-egyenlőtlenséget.
 

313. Hogyan szól a megfelelő egyenlőtlenség-konkáv, tágabb értelemben konvex, ill. tágabb értelemben konkáv függvényekre?
 

314. A 312. feladat eredményét felhasználva döntsük el, hogy az x2, x, x3, 1x függvények hol konvexek, hol konkávok.
 

315. Legyen p1 és p2 pozitív szám, q1=p1p1+p2, q2=p2p1+p2 (tehát q1+q2=1). Nevezzük az x1, x2 számok p1 és p2, ill. q1 és q2 súlyokkal súlyozott számtani-, négyzetes-, illetőleg harmonikus közepének sorra a
p1x1+p2x2p1+p2=q1x1+q1x2;p1x12+p2x22p1+p2=q1x12+q2x22;p1+p2p1x1+p2x2=1p1x1+p2x2p1+p2=1q1x1+q2x2


kifejezéseket. Bizonyítsuk be, hogy a súlyozott harmonikus közép nem lehet nagyobb, mint a súlyozott számtani közép, ez pedig nem nagyobb a súlyozott négyzetes középnél. Mikor lehetnek egyenlők?
Írjuk fel a megfelelő egyenlőtlenségeket, ha p1=p2, (q1=q2).
 

*
 

A ,,súlyozott'' jelző a fizikára emlékeztet. Mindjárt meglátjuk, mi indokolja ezt az elnevezést.
 

316. Az X-tengelynek az x1 pont és x2 pont közti szakaszát képzeljük el súlytalan rúdként a koordináta-síkból kivágva; helyezzünk el az x1 végpontban p1 súlyt, az x2 végpontban p2 súlyt. Az X tengely melyik pontjában lesz a rúd súlypontja?
Helyezzünk el az y=f(x) görbén fekvő (x1,y1) pontban p1, súlyt, az (x2,y2) pontban pedig p2 súlyt. Ha ezeket képzeljük el súlytalan rúddal összekötve, akkor hol lesz most a rúd súlypontja? (Mi lesz az abszcisszája és mi lesz az ordinátája?)
Mit jelent a Jensen-egyenlőtlenség ,,fizikailag''? Mi van ha p1 és p2 súlyok egymással egyenlők?
Ebből a fizikai értelmezésből a Jensen-egyenlőtlenség egy általánosításához jutunk, ha kettő helyett több súlyt helyezünk el a görbe különböző pontjaiban: Három pont súlypontját úgy határozhatjuk meg, hogy az első két pont súlypontjába a két pont egyesített súlyát helyezzük, majd képezzük az így keletkezett pontnak és a harmadik pontnak a súlypontját és ugyanígy vesszük sorra hozzá a további pontokat.
 

317. Számítsuk ki az (x1,y1),(x2,y2),...,(xk,yk) pontokban rendre elhelyezett p1,p2,...,pk súlyok súlypontjának abszcisszáját és ordinátáját.
Bizonyítsuk be, hogy bármilyen sorrendben is vesszük a pontokat a fenti eljárásban, ugyanazt a súlypontot kapjuk. Ugyanezt a számot kapjuk-e akkor is, ha a pontokat csoportokra választjuk és az egyes csoportok súlypontjainak számítjuk ki a súlypontját?
Bizonyítsuk be a 312. feladat alapján, hogy egy függvény akkor és csak akkor konvex, ha minden x1,x2,...,xk-ra és minden pozitív p1,p2,...,pk-ra
f(p1x1+p2x2+...+pkxkp1+p2+...+pk)≤≤p1f(x2)+p2f(x2)+...+pkf(xk)p1+p2+...+pk


vagy minden pozitív q1,q2...qk-ra melyek összege 1,
f(q1x1+q2x2+...gkxk)≤q1f(x1)+q2f(x2)+...+gkf(xk).(D')
Mikor állhat fenn egyenlőség? (Mi az egyenlőtlenség fizikai értelme?)
Ez a ,,többtagú (k-tagú) súlyozott Jensen-egyenlőtlenség''. Hogy szól a k-tagú szimmetrikus Jensen-egyenlőtlenség?
Látszólag semmire sem jutottunk. Azzal a céllal fordultunk a geometriához, hogy innen kapjunk segítséget újabb egyenlőtlenségek felkutatásához. Végül a fordított feladatra jutottunk s éppen geometriai tulajdonságok szigorú bizonyításához volt szükségünk egyenlőtlenségek bebizonyítására. Az utolsó feladatban azonban már láttunk példát arra, hogy bizonyos egyenlőtlenségek ismeretében a geometriai szemlélet rávezetett arra, hogy további egyenlőtlenségek helyességére tudjunk következtetni. További feladatunk az lesz, hogy olyan, lehetőleg egyszerű tulajdonságokat keressünk, amelyekből már a függvény konvex voltára következtethetünk, amelyekből tehát a konvexséget kifejező további egyenlőtlenségek helyessége már levezethető.
1Ezzel teljes megoldását adtuk a 285. feladatnak.
Megoldotta: Dursi E., Kántor S., Kovács L., Villányi O., Zobor E. Részben: Rédly E., Reichlin V., Tornyos F., Zatykó L.

2Pozitív szám tört hatványán (valamilyen gyökén) mindig ennek a pozitív értékét értjük.

3Ezzel a 286. feladatnak adtuk megoldását. Megoldotta: Kántor S. Részben: Rédly E., Zobor E., Zatykó L.

4Ezzel a 287. feladatnak adtuk megoldását. Megoldotta: Durst E., Kántor S., Kovács L., Reichlin V., Villányi O., Zatykó L., Zobor E. Részben: Rédly E.

5Valóban a két oldal különbsége

a2+b22-(a+b2)2=a2-2ab+b24=(a-b2)2≥0