Cím: Egyenlőtlenségek (1.)
Szerző(k):  Aczél János ,  Surányi János 
Füzet: 1951/május, 12 - 19. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Középértékek
 

Az iparban, kereskedelemben és a gyakorlati élet számtalan területén számolunk középértékekkel. Aki munkatervet akar készíteni, tudnia kell, hogy mennyi munkát szokott elvégezni naponta. Nem egy gyönge napját fogja alapul venni, hiszen nem annyit szokott végezni általában, de tervét valószínűleg nem tudná keresztülvinni akkor sem, ha friss erőben, teljes figyelemmel elért egyszeri legjobb teljesítményét akarná mindjárt, rendszeresen, naponta túlszárnyalni. Úgy jár el helyesen, ha hosszabb időre eső napi átlagteljesítményét veszi alapul és célul is átlagos teljesítményének az emelését tűzi ki. Hasonlóan egy üzem vagy üzemrész munkájára is a dolgozók teljesítményének átlaga a jellemző. A közlekedési vállalatoknak ismerniük kell az utasok napi átlagos számát; külön azt, hogy az úgynevezett csúcsforgalomban mennyi az utasok száma, hogyan változnak ezek az átlagok évszakonként és még számtalan adatot, amik mind valamilyen átlagértéket jelentenek. A KÖZÉRT, vagy az állami áruházak központjának ismernie kell (sok egyéb mellett) az egyes üzletek átlagos forgalmát; a háziasszonynak azt, hogy mennyibe kerül háztartása átlagosan, naponta; a kutató kísérleteit többször ismétli, mert azok nem folynak le kétszer hajszálra egyező módon. Az így megismételt mérések kissé eltérő eredményeinek ismét középértékét veszi.
Középértéket sokféleképpen lehet számolni. Általában a feladat természete dönti el, hogy mikor melyiket alkalmazzuk. Térjünk vissza például a bevezetőben említett munkáshoz. Ő alkatrészekből állít össze egy tárgyat. Egy hétig jegyzi, hogy mennyit készített el naponta: (az egyszerűbb számítás kedvéért képzeljük úgy el, mintha minden hétköznapon egyformán 8 órát dolgozna.) 201, 209, 225, 231, 224, 213. Most azt szeretné tudni, hogy hány darabot kellett volna készítenie naponta, hogy minden nap pontosan ugyanannyit készítve érje el ugyanazt a heti termelést. Ezt a számot s-sel jelölve, 6 nap alatt 6s darabot készítene egész egyenletes munkával. Valójában elkészített 201+209+225+231+224+213 darabot. Így s-re adódik, hogy
s=201+209+225+231+224+2136=13036=21716.
Itt tehát az átlagot úgy számítottuk ki, hogy a számok összegét osztottuk az összeadandók számával. Az így számított mennyiséget az adott számok számtani közepének szoktuk mondani. ,,Közép''-nek vagy ,,középérték''-nek azért nevezzük, mert az előforduló számok legkisebbike és legnagyobbika közé esik, hisz s számára úgy adódna 201 vagy 231 érték, ha mindegyik összeadandó helyébe 201-et, ill. 231-et írnánk. Az első esetben nyilván csökkentenénk, a másodikban növelnénk a tört értékét. Általában az a1,a2,...,an számok számtani közepén az
a1+a2+...+ann
értéket értjük. Igaz, hogy a gyakorlatban legtöbbször ez a középérték szokott előfordulni, de távolról sem mindig, és az is előfordul, hogy helytelenül használják ezt a középértéket más középértékek helyett. Lássunk erre is példát.
Összetettebb munkánál nem elegendő az elkészült darabokat megszámlálni, hanem a munka egyes folyamatait külön kell megfigyelni. Ilyenkor azt szokták mérni, hogy a munkafolyamat egyszeri elvégzéséhez mennyi időre van szükség. Most vegyük a következő példát: Egy szakmunkás betanít valakit. Társa a legtöbb munkafolyamatban el is érte mesterét, csak egy nagy gyakorlatot igénylő munkafolyamat megy még lassan. Ezt a szakmunkás 6 mp. alatt végzi el, tanuló társa 10 mp. alatt. Mennyi kettőjük átlagteljesítménye ebben a munkafolyamatban ? Elhamarkodott volna rávágni, hogy 8 mp. Ismét az a kérdés, hogy mennyi idő alatt kellene elvégezniük azt a munkafolyamatot ahhoz, hogy összesen ugyanannyiszor végezzék el, ahányszor ténylegesen elvégzik különböző teljesítményeik mellett, ha mindketten egyenlő idők alatt végeznék el. Valamilyen i másodperc idő (például 1óra=3600mp, vagy 1 munkanap) alatt a szakmunkás i/6-szor, a tanuló i/10-szer végzi el a folyamatot, ha pedig mind a ketten h idő alatt végeznék el egyszerre, akkor i idő alatt együtt 2i/h-szor végeznék el, így h-t a 2ih=i6+i10 összefüggés adja meg. Innen
1h=16+1102ésh=116+1102=712mp.
Itt tehát az átlagos idő reciprok értéke az egyes idők reciprok értékeinek a számtani közepe. Ennek a számtani középnek a reciproka adja tehát a közepes időt. Ezt a középértéket harmonikus középnek nevezik. Általában két szám, a és b harmonikus közepe:
h=11a+1b2=2aba+b.

Harmadik példánkat a fizikai mérések köréből választjuk. Igen nagy pontossággal lehet tömeget mérni. Kutató laboratóriumban, gyógyszertárban használt mérlegek pár száz gramm mérésére alkalmasak, de ugyanakkor még a gramm ezredrészére is érzékenyek, tehát a mérendő alig százezred részére. Ilyen pontos méréseknél gondosan meg kell vizsgálni, hogy nem hamisíthatja-e meg valami a mérés eredményét. A mérleg alapelve, hogy ha egy rudat pontosan a közepén alátámasztunk, akkor a végeire függesztett testek akkor lesznek egyensúlyban, ha egyenlő a tömegük. Még igen pontosan készített mérlegeknél is előfordulhat azonban, hogy a karok hosszában hajszálnyi eltérések legyenek, ha ezt is a milliméter ezredrészéig szigorúan vizsgáljuk. Ezt a hibát például úgy küszöbölhetjük ki, hogy a mérendő testet kétszer mérjük meg: egyszer a bal serpenyőbe tesszük, és a jobba helyezzük a súlyokat, azután megcseréljük. Ha a kétszeri mérés eltér, akkor a karok nem egyenlők. Ekkor a két mérés eredményének valamilyen középértéke a test valódi tömege. Annak megállapításához, hogy milyen középről van szó, a fizikából kell tudnunk annyit, hogy ha mérlegkarok nem egyenlőek, akkor az egyensúlyt tartó tömegek fordítva aránylanak, mint a megfelelő mérlegkarok hosszai. Legyen a mérendő tömeg m, a mérlegkarok hossza k1 és k2, és a k1 hosszúságú karon lévő serpenyőbe téve a mérendő súlyokat, m1-nek mérjük a test tömegét, ha pedig a mérendő testet helyezzük az első serpenyőbe, és a k2 hosszúságú karon egyensúlyozzuk ki, akkor m2-nek találjuk; tehát a k1 karon lévő m tömeggel a k2 karon m1 súly, a k2 karon lévő m tömeggel pedig a k1 karon m2 súly tart egyensúlyt. Így m1m=k1k2 és mm2=k1k2. Innen m1m=mm2, tehát m2=m1m2, vagy* m=m1m2. Az m1 és m2-ből ilyen módon számított középértéket mértani középnek nevezzük. Ha néhány esetben számítást végzünk, az így számított közepet, ha néha nagyon kevéssel is, de mindig kisebbnek találjuk a számtani középnél.
m1   m2   m=m1m2   m1+m22109,11111109,9594110,45183,1184,1183,5484183,55107,1107,8107,4494107,451935

Ha ez mindig így van, akkor a súlyosabb hiba nem is az, hogy pontatlan értéket adna, ha gondolkodás nélkül számtani középpel számolnánk, hanem hogy ez a hiba mindig egy irányban tér el a helyes értéktől. Vizsgáljuk meg, hogy valóban igaz-e bármely két a és b számra, hogy a számtani közepük nagyobb, mint a mértani. Természetesen a két számnak pozitívnak kell lennie, mert ha mindkettő negatív, akkor a számtani közép is negatív, s így biztosan kisebb a mértani középnél, ha pedig az egyik negatív, a másik pozitív, akkor a mértani középnek nincs értelme. Ha a két szám egyenlő, akkor a számtani közép is, a mértani is a közös értéküket adja. Megvizsgálandó tehát az az eset, amikor a két szám pozitív és különböző, mondjuk a és b, ez a két szám a,b≧0, a≠b. Úgy sejtjük, hogy ekkor
a+b2>ab.(1)
Elég ehelyett azt megmutatni, hogy
a+b2-ab>0,
mert ebből a negatív tagot újra átvíve a jobboldalra, nyerjük az első egyenlőtlenséget. De ha ezt a kifejezést jól megfigyeljük, látjuk, hogy ez teljes négyzet:
a+b2-ab=12(a+b-2ab)=12(a-b)2>0,
mert valós szám négyzete pozitív. Ezzel bebizonyítottuk a második, tehát a mondottak szerint az (1) egyenlőtlenséget is. Két pozitív szám számtani közepe tehát mindig nagyobb, mint a mértani, csak akkor egyenlők, ha a két szám egyenlő.
A talált egyenlőtlenségnek egy érdekes speciális esetét kapjuk, ha b-nek a reciprokát vesszük: a+1a2>a1a=1, azaz a+1a>2; ha a≠1a azaz a≠1. Egy számnak és reciprokának összege mindig több 2-nél, kivéve, ha e szám 1. Ennél az érdekes eredménynél is érdekesebb az, hogy ebből az egyszerűbb egyenlőtlenségből is következik az általánosabb egyenlőtlenség: írjunk a helyett xy-t, ahol x≠0, y≠0. Mivel 1/x/y=y/x, tehát egyenlőtlenségünkből xy+yx>2, ha xy≠1, azaz x≠y. Szabad az egyenlőtlenséget a pozitív xy értékkel végigszorozni, és kapjuk, hogy
x+y≥2xy,azazx+y2>xy,hax≠0,y≠0,x≠y.
(Könnyű látni, hogy az első két feltétel, mely a kiinduló egyenlőtlenséghez volt szükséges, az utolsó egyenlőtlenségnél el is hagyható.)
Nyert egyenlőtlenségünket felhasználhatjuk a következő feladat megoldására: keressük az egyenlő kerületű téglalapok közül a legnagyobb területűt. 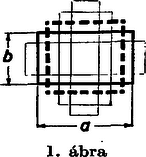a és b-vel jelöljük a téglalap oldalait, (1. ábra) akkor kerülete K=2(a+b) és területe T=ab. a és b értékét szabadon választhatjuk, de csak úgy, hogy közben a kerület K nagysága ne változzék.
 
 

Keressük ezek közt azt a téglalapot, amelyre a terület a legnagyobb. De az (1) egyenlőtlenségből rögtön nyerünk egy összefüggést T és K közt.
T=ab<a+b2=K4,
kivéve, ha a=b (vagyis ha négyzettel van dolgunk), ekkor éppen egyenlőség áll fenn. De az összes bennünket érdeklő téglalapok kerülete ugyanakkora, így a K4 érték is mindegyiknél ugyanaz, tehát a változó terület mindig kisebb az állandó K4-nél, csak akkor egyenlő vele, ha a=b, ha téglalapunk négyzet. Ez utóbbi esetben lesz tehát legnagyobb a terület négyzetgyöke és mivel nagyobb pozitív szám négyzete is nagyobb, mint egy kisebb pozitív számé, ebből következik, hogy maga a terület is az egyenlő téglalapok közül a négyzetnél a legnagyobb.
Általánosabban megmutatható, hogy az összes egyenlő kerületű négyszögek közül a négyzet területe a legnagyobb. Hasonlóan az egyenlő kerületű 5 szögek, 6 szögek általában bármilyen oldalszámú sokszögek közül a szabályos ugyanannyi oldalú sokszög területe a legnagyobb. Ha pedig semmit sem kötünk ki a görbe alakjáról, akkor arra az eredményre jutunk, hogy az összes egyenlő kerülete görbék közül a kör zár be legnagyobb területet. Ezt a tételt szintén egy egyenlőtlenség formájában lehet kifejezni és bizonyítani is. Jelöljük a görbe kerületét K-val, az általa bekerített területet T-vel. Ekkor minden görbére K2>4πT, kivéve a kört, mert arra egyenlőség áll. Ezt az egyenlőtlenséget nevezik izoperimetrikus (egyenlő kerületű) egyenlőtlenségnek. * Ez valóban az említett tételt fejezi ki, mert a K kerületű kör sugara r=K2π és így K2=4π2r2=4π(πr2). Az egyenlőtlenség baloldalán tehát a K kerületű kör területének 4π-szerese áll és az egyenlőtlenség szerint ez nagyobb minden más görbe által bezárt terület 4π-szeresénél.
Egyelőre csak egy egyszerű egyenlőtlenséget bizonyítottunk és mutattuk be egy alkalmazását. Hasonló egyenlőtlenségekre azonban a matematika különböző területén és a matematika alkalmazásában lépten-nyomon szükség van. Ezekről az egyenlőtlenségekről és alkalmazásaikról kívánunk néhány következő cikkben valamelyest képet adni. Az egyes egyenlőtlenségeket és alkalmazásaikat többnyire ti magatok fogjátok megoldani a kitűzött feladatok és gyakorlatok keretében. A ti megoldásaitok fogják továbbvinni a tárgyalást. A vastag számmal jelzett feladatok lesznek különösen fontosak a továbbhaladáshoz. Ezek megoldásai is ugyanaddig küldhetők be, mint minden feladatéi, de már a következő számban közöljük is őket, így aki megoldotta, lehetőleg mielőbb küldje be megoldását.
 

279. Az 1. ábrán felrajzoltunk néhányat az egyenlő kerületű téglalapok közül, úgyhogy középpontjuk közös és oldalaik párhuzamosak. Ha megrajzoltuk volna valamennyi ilyen téglalapot, fekete folt keletkezne a papíron. Milyen alakú lenne ez a folt ?
 

280. Egyenlő területű téglalapok közül melyiknek legkisebb a kerülete ?
 

281. Ha megrajzolnánk az összes egyenlő területű téglalapot közös középponttal és párhuzamos oldalakkal, milyen alakú folton feketítenénk be a papirost ?
 

282. Egyenlő magasságú derékszögű háromszögek közül melyiknek az átfogója a legkisebb ? (Magasságon természetesen a derékszögű csúcsból az átfogóra bocsátott magasságot értjük.)
 

283. Egyenlő átfogójú derékszögű háromszögek közül melyiknek a magassága a legnagyobb ?
 

284. A 282. és 283. feladatban megrajzolva a feltételnek megfelelő összes háromszöget úgy, hogy közös legyen a magasságuk ill. közös legyen az átfogójuk, ezek milyen foltot takarnának le ?
 

A továbbiakhoz egyenlőtlenségek helyes átalakításában kell biztonságra szert tenni. A számtani középről úgy döntöttük el, hogy nagyobb a mértaninál, hogy az utóbbit levontuk belőle és megállapítottuk, hogy a különbség pozitív. Különösen egyenlőtlenségek átalakításának helyességét leggyakrabban ilyen úton sikerül ellenőrizni.
 

285. Bizonyítsuk be, hogy ha A>B és c tetszőleges valós szám, akkor
a) A+c>B+c;
b) ha c pozitív, cA>cB; ha c negatív, cA<cB;
Továbbá, ha A>B és A is, B is pozitív, akkor
c) A2>B2,A3>B3,..., An>Bn minden pozitív egész n-re;
d) 1A<1B, 1An<1Bn minden pozitív egész n-re;
e) ha A>B és C>D, akkor A+C>B+D és
f) ha még A, B, C, D mind pozitívok is, akkor AC>BD.
 

Itt egyes mennyiségekre megszorításokat tettünk. Volt-e erre mind szükség ? Hogy egy feltételből nem engedhetünk, azt úgy mutathatjuk meg, hogy példát mutatunk, melyben a kérdéses feltevés nem teljesül, de a várt következménynek is az ellenkezője igaz. Már egyetlen ilyen ,,ellenpélda'' is elegendő, hogy meggyőzzön róla: a feltevést elhagyva nem lehet általános érvényű a tétel: nem igaz kivétel nélkül minden esetben, hisz egy kivételt már találtunk.
 

286. Szükségesek-e az előző feladatban az egyes feltételek, vagy engedhetnénk belőlük ?
 

287. Legyenek A, B, C, D tetszőleges valós mennyiségek. Hasonlítsuk össze az A+C és B+D továbbá az AC és BD mennyiségeket, ha A<B és C=D.
*Gyökmennyiségeken azok pozitív értékét fogjuk általában érteni.

*Erről a kérdéskörről Fejes Tóth Lászlónak jelent meg most részletes magyar nyelvű dolgozata: Az izoperimetrikus probléma. Matematikai Lapok I. (1951) 363‐383. old. Folytatása sajtó alatt.