Cím: Az 1950. évi Középiskolai Matematikai Lapok országos matematikai tanulóversenye
Füzet: 1951/március, 229 - 240. oldal  PDF  |  MathML 
Témakör(ök): Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Mint lapunk előző száma már hírt adott róla, június 3-án d. u. 3‐7 óráig rendeztük meg harmadízben (egy évi megszakítás után) országos matematikai tanulóversenyünket. A verseny Budapesten központi helyen, továbbá az ország 44 középiskolájában folyt kezdő és haladó csoportban. A kezdők versenyén III. és IV. osztályos tanulók nem vehettek részt. Előző számunk ismertette a kitűzött feladatokat is. A dolgozatokat négytagú bizottság vizsgálta felül és tett javaslatot a Bolyai János Matematikai Társulat választmányának a díjak odaítélésére. A bizottság tagjai Hajós György egyetemi tanár, Lőrincz Pál, Neukomm Gyula tanulmányi felügyelők és Surányi János felelős szerkesztő.
A bizottság örömmel látta, hogy a verseny iránt idén egész rendkívüli érdeklődés nyilvánult meg, s a dolgozatok soha nem tapasztalt mennyiségben özönlöttek az ország minden részéről. A kezdők versenyén 484-en, a haladókén pedig 172-en adtak be dolgozatot. A dolgozatok minősége még nem áll arányban a nagy érdeklődéssel. Ezen a téren komoly javulásra van szükség és reméljük, hogy diákjaink rendszeres munkája a kartársak támogatásával és a komoly fejlődés előtt álló szakköri mozgalom ezt rövidesen meg fogja hozni.
Sajnálattal tapasztalta a bíráló bizottság, hogy a verseny néhány helyen nem folyt kellő komolysággal és így azonos, vagy majdnem azonos szövegű dolgozatok érkeztek.
Különösen sajnálatos, hogy a kezdők versenyének éppen az a két dolgozata egyezik gondolatról gondolatra, melyek egyedül tartalmaznak mindhárom feladatra helyes megoldást. Ez annál feltűnőbb, mert a harmadik feladat egyébként helyes megoldását mindkét dolgozat szerzője fölöslegesen indirekt bizonyításnak fogalmazza. E két versenyzőt így ki kellett zárni a versenyből.
Miután így a számbajövő dolgozatok közt nem volt olyan, amelyik mindhárom feladatot helyesen megoldotta volna, a bizottság első díj kiadását nem javasolja. Második díjra javasolja Horváth Ákosnak a szentendrei gimnázium II. osztályos tanulójának dolgozatát. A számbajövő dolgozatok szerzői közül egyedül ő ad korrekt megoldást az első feladatra. A másodiknál nem veszi észre, mint a pályázók egyike sem, hogy 90∘ nem megoldása a feladatnak. A harmadik feladat leírása teljesen zavaros, ha látott is valamit a megoldást szolgáltató kapcsolatból.
Bakos István, a mezőkövesdi gimnázium II. osztályos tanulójának, Kálmán Lajos, a budapesti Berzsenyi Dániel gimnázium II. osztályos tanulójának és Szekerka Pál, a budapesti Rudas László gimnázium II. osztályos tanulójának dolgozatát harmadik díjra ajánlja a bizottság. Az első feladatnak mindhárman csak egy részmegoldását nyerik, mivel az egyenlőtlenség végigszorzásánál nem ügyelnek a szorzó előjelére. A második feladatnál ők is elfogadják a 90∘-ot megoldásul. Szekerka a sinus-érték alapján adódó mindkét szöget szintén elfogadja megoldásnak. A harmadik feladatra mindhárman helyes megoldást adnak. Bakos felveti a pont pályája hosszának kérdését, azonban nem tud rá helyes választ adni. A megoldás fogalmazása Szekerkánál a legvilágosabb.
Javasolja a bizottság, hogy Rédly Elemér (a szentendrei gimnázium I. osztályos tanulója) dolgozata, dicséretet nyerjen. Ő a harmadik feladatnak lényegében helyes megoldását adja. A második feladattal, mint első osztályos, nem foglalkozik. Az első feladatnál próbálgatáshoz folyamodik, majd grafikus ábrázolással próbálja megoldását teljessé tenni.
A haladók versenyén öt dolgozat ad többé-kevésbé elfogadható megoldást mindhárom feladatra, mindhárom feladat pontos megoldását azonban csak Fodor László, a betettyóújfalusi Arany János gimnázium IV. osztályos tanulója adja. Az ő dolgozatát javasolja a bizottság első díjra.
Második díjra javasolja Korányi Ádám (a szegedi Klauzál gimnázium IV. osztályos tanulója) és Villányi Ottó (a szentendrei gimnázium II. osztályos tanulója) dolgozatát. E két dolgozat mutatja a legnagyobb változatosságot, legkülönbözőbb gondolatokat. Korányi a második feladatra három elegáns megoldást ad. (Ezek közül a második igen szellemes szimmetria-meggondolást alkalmaz, azonban hiányzik a szélsőérték létezésének igazolása.) A harmadik feladat megoldásánál hibásan hivatkozik a legnagyobb szöggel szemközti átlóra, nem is ezt használja fel. Villányi az első feladatra két megoldást ad, bár az első nem egész korrekt. Mindkettőben bizonyítja, hogy az összeg 36-tal is osztható, ha 18-cal osztható. A harmadik feladatra adott első megoldása egész elhibázott, második megoldása azonban helyes és egyszerű gondolaton alapuló megoldás. Villányi teljesítménye annál is figyelemre méltóbb, mert mint II. osztályos indult a haladók versenyén.
Szántó István (a szegedi Móra Ferenc gimnázium IV. osztályos tanulója) és Zergényi Erzsébet (a soproni állami általános leánygimnázium IV. osztályos tanulója) dolgozatát harmadik díjra javasolja a bizottság. Szántó a második feladatban ügyesen csökkenti le a határozatlan mennyiségek számát egyre, azután azonban differenciálszámítást alkalmaz, a kínálkozó sokkal egyszerűbb módszerek helyett. A harmadik feladatban ügyesen fogja meg a lényeget, de hibásan hivatkozik a bizonyításban a legrövidebb oldalra. Zergényi a második feladatnál szintén differenciálszámítást használ. Nem mutatja meg, hogy valóban van szélsőérték és milyen. Igen tömör, világos a harmadik feladat megoldása és az elsőé is, bár itt a rövidség hiányosságra is vezetett.
A Választmány 1950. október 10-i ülésén elfogadta a bizottság javaslatát és az első díjat 300, a második díjat 200, a harmadik díjat 100 forintban állapította meg.
Az alábbiakban ismertetjük a feladatok megoldását.

 


Kezdők versenye:
1. Az x változó mely értékeire teljesül az
x-1x-2<x+3x(1)
egyenlőtlenség?
 

Ez a feladat okozta a versenyzőknek a legtöbb nehézséget. A feladat ugyan nem nehéz, de az indulók járatlanok voltak egyenlőtlenségek kezelésében. Legtöbben minden átalakítást gondolkozás nélkül úgy hajtottak végre, mint egyenleteknél szokásos, és nem gondoltak arra, hogy ha negatív számmal szoroznak, akkor abból lesz kisebb szám, ami eredetileg nagyobb volt.
 

I. megoldás: Egyszerűbb alakra hozzuk az egyenlőtlenséget. Elegendő az 1-gyel kisebbített
1x-2<3x(2)
egyenlőtlenséget igazolnunk, mert ehhez 1-et adva visszanyerjük az eredetit.
Ábrázoljuk a két oldalon lévő függvényt grafikusan.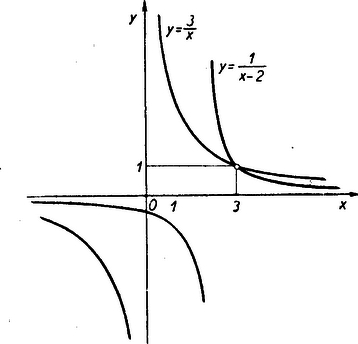
 
 

A baloldalinak 2-nél, a jobboldalinak 0-nál szakadása van. E helyeken kívül csak ott válhatik az egyik a másiknál kisebből nagyobbá, ahol közben egyenlők lesznek. Mivel ez csak x=3-nál következik be, az ábra mutatja, hagy (2) csak 0 és 2 közt és 3-nál nagyobb x-ekre teljesül.
 

II. megoldás: A (2) egyenlőtlenségről azonnal látjuk, hogy teljesül, ha 0<x<2, mert ekkor a baloldal negatív, a jobb viszont pozitív. Ha x negatív, vagy 2-nél nagyobb, akkor a két oldal egyező előjelű s így reciprokaik között az ellentétes egyenlőtlenségnek kell fennállnia:
x-2>x3,3x-6>x,x>3.
A feltételnek tehát a 0 és 2 közti és a 3-nál nagyobb számok tesznek eleget, s így az (1) egyenlőtlenségnek is.
 

III. megoldás: Áttekinthetőbbé válik a feladat, ha úgy alakítjuk, hogy egy függvényről azt kelljen eldönteni, mely x értékekre pozitív az értéke. A baloldalt levonva az egyenlőtlenségből
0<x+3x-x-1x-2=2(x-3)x(x-2),
Ez akkor teljesül, ha a számláló és nevező egyező előjelű, tehát
a) ha x-3>0 és x(x-2)>0. Utóbbi mindig teljesül, ha az előbbi teljesül, tehát minden 3-nál nagyobb szám megfelel a feltételnek.
b) ha x-3<0 és x(x-2)<0, azaz a második egyenlőtlenségben szereplő két tényező ellenkező elöjelű. Kell tehát hogy x nulla és kettő között legyen, a az ilyen x-ek az első egyenlőtlenséget is kielégítik. A feltételnek tehát a
0<x<2  és  x>3
feltételeket kielégítő számok felelnek meg.
 

2. Oldjuk meg az
1-sinxcosx=12
egyenletet.
 

Erre a feladatra is alig érkezett pontos megoldás, bármilyen egyszerű is a feladat, mert a versenyzők kellő figyelem nélkül csak gépiesen számoltak. Így legtöbben 90∘-ot is megoldásul kapták és ezt is elfogadták az egyenlet gyökének.
 

I. megoldás: Bevezetjük mindkét szögfüggvény helyett a tangenst:
1-sinxcosx=1cosx-tgx=1+tg2x-tgx.
Egyenletünk ezek alapján így írható:
1+tg2x=12+tgx,
négyzetre emelve
1+tg2x=14+tgx+tg2xtgx=34.


Ennek két szög felel meg, azonban a 180∘-nál nagyobb megoldásának a sinusa negatív, s így az eredeti egyenlet baloldalán 1-nél nagyobb szám állna, tehát ez nem megoldása az eredeti egyenletnek. A hegyesszög megoldásra sinx=35, cosx=45 és teljesül az eredeti egyenlet. A megoldás ebből x=36∘58'.
 

II. megoldás: Fejezzük ki a baloldalt sinx segítségével:
1-sinxcosx=1-sinx1-sin2x=(1-sinx)21-sin2x=1-sinx1+sinx.
Ezt felhasználva egyenletünk:
1-sinx1+sinx=12vagy1-sinx1+sinx=14.
Innen sinx=35 és az eredeti egyenletből cosx=2(1-sinx)=45. x tehát hegyes szög. x=36∘58'.
 

III. megoldás: A számlálóban egynél kisebb szám kell hogy álljon, mert a nevező mindig egynél kisebb; tehát sinx pozitív, a nevezőben pedig pozitív szám áll, mert a számlálóban az áll. Így cosx is pozitív. E szerint x hegyes szög. Ábrázoljuk a szereplő mennyiségeket egy egységnyi sugarú negyedkörben. Ábránkon AB=sinx. Meghúzva az OA-val párhuzamos 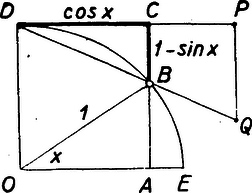DC érintőt, BC=1-sinx és CD=OA=cosx, tehát
tgBDC∢=BCCD=1-sinxcosx=12
kell legyen.
 
 

Ennek alapján megoldhatjuk grafikusan az egyenletet: Egy OAD derékszög szárai közé O középpontú DE negyedkört húzunk. A D-ben húzott érintő egy tetszőleges P pontjában merőlegesen lefelé meghúzzuk a PQ=1/2DP távolságot. A DQ egyenes metszi ki a körből azt a B pontot, melyre EOB∢=x. Ezt tehát közvetlenül lemérhetjük. Befejezhetjük a megoldást számítással is. BDC∢ mint húr és érintő közti szög, kerületi szög. A hozzátartozó középponti szög BOD∢=90∘-x, így BDC∢=45∘-x2, tehát a keresett szögre
tg(45∘-x2)=12
Innen x=36∘58'.
Megjegyzés: Az
1-sinxcosx=tg(45∘-x2)
összefüggés természetesen tisztán számítással is igazolható.
 

3. Egy egyenlőszárú trapézt vágjunk ketté egyik átlójával. Az egyik levágott háromszöget csúsztassuk a síkban, úgy, hogy a háromszög két csúcsa továbbra is a másik háromszöget határoló két trapézoldalon vagy meghosszabbításukon mozogjon. Milyen pályán mozog eközben a harmadik csúcs?
 

Megoldás: Legyen a trapéz két párhuzamos oldala AB és CD. A nem párhuzamos oldalak AD és BC. A BCD▵-et mozgatjuk. A háromszög AD oldalon mozgó csúcspontja D', az AB-n mozgó B', a harmadik csúcs 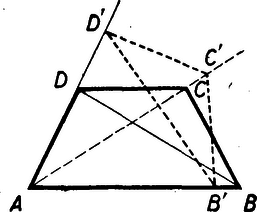C'.
 
 

Az AB'C'D' négyszög húrnégyszög, mert tudjuk, hogy a szimmetrikus trapéz húrnégyszög, s így D'AB'∢+B'C'D'∢=DAB∢+BCD∢=180∘.
Húzzuk meg a négyszög AC' átlóját. Akkor B'AC'∢=B'D'C'∢, mint kerületi szögek. De minthogy B'D'C'∢=BDC∢=BAC∢, azért B'AC'∢=BAC∢. Ez azt jelenti, hogy az ABCD trapéz AD és az AB'C'D' négyszög AC' átlója egyenlő szöget zár be AB-vel, tehát a két egyenes egybeesik. Minthogy C' a mozgó háromszög harmadik csúcspontja, azért a harmadik csúcspont a trapéz másik átlóján mozog, azaz fennáll a következő tétel:
Ha egy egyenlőszárú trapéz egyik átlóját meghúzzuk és az így kapott két háromszög közül az egyiket úgy toljuk el a síkban, hogy a háromszög két csúcsa továbbra is a másik háromszöget határoló két oldalon maradjon, akkor a háromszög harmadik csúcspontja a trapéz másik, meg nem húzott átlóján mozog.
 

Szekerka Pál
 

Megjegyzés: A harmadik csúcs eljuthat az átló A csúcson túli meghosszabbításra is, ha a két háromszögcsúcs egymásután átjut a megfelelő trapézoldalak A-n túli meghosszabbítására. Mivel a harmadik csúcs az AB oldaltól nem lehet a BC szakasznál nagyobb távolságra, az AD oldaltól pedig CD-nél nagyobb távolságra, így legtávolabbi helyzetét az A csúcs mindkét oldalán akkor éri el, mikor a belőle induló háromszögoldalak merőlegesek az AB ill. AD egyenesre. (Ez egyidejűleg következik be épp a felhasznált szögösszefüggések folytán.) Míg a háromszöget úgy mozgatjuk, hogy mindkét csúcsa egyszer megtegye oda és vissza a számára lehetséges legnagyobb utat, addig a harmadik csúcs egyszer bejárja oda és vissza a szélső helyzetek közti szakaszt.
 


Haladók versenye:
 

1. Három szomszédos egész szám köbének összege mikor osztható 18-cal?
 

I. megoldás: A három szám közt kell hogy egy páros és két páratlan legyen, mert különben az összeg páratlan. Ehhez a középső számnak kell párosnak lennie.
A köbösszegnek ezenkívül 9-cel is oszthatónak kell lennie. A három szám közül az egyik osztható 3-mal, s ennek a köbe mindenesetre osztható 9-cel, tehát elég a másik két köb összegét vizsgálnunk. Ezek egyike mindig egy 3-mal osztható szám után a másika egy hárommal osztható szám előtt áll, tehát ilyen alakban írhatók: (3k+1), (3l-1). Köbeik összege:
(3k+1)3+(3l-1)3=27k3+27k2+9k+1+27l3--27l2+9l-1=9(3k3+3k2+3l3-3l2+k+l).


Ez mindig osztható 9-cel, tehát három egymásutáni szám köbe osztható 18-cal, ha a középső szám páros, különben pedig nem osztható.
 

II. megoldás: Mint előbb láttuk, kell hogy a középső szám páros legyen. Jelöljük azt 2n-nel, akkor a kérdéses összeg
(2n-1)3+(2n)3+(2n+1)3=24n3+12n==12n(2n2+1)=12n(3n2-(n2-1))==36n3-12(n-1)n(n+1).


Mivel három egymásutáni szám közt mindig van páros és van 3-mal osztható, így szorzatuk mindig osztható 6-tal, tehát a kivonandó többszöröse 12⋅6=72-nek. Ezzel többet is bizonyítottunk, mint ami a feladat volt: Három egymásután egész szám köbének az összege csak akkor osztható 18-cal, ha a középső szám páros, ilyenkor azonban mindig osztható 36-tal is az összeg.
 

2. Az ax2+bx-c=0 egyenletben a, b, c pozitív számok és a2=bc. Mi az eggyel növelt gyökök szorzatának lehetséges legnagyobb értéke, és ezt az a, b, c milyen értékei mellett veszi fel?
 

Ezt a feladatot legtöbben differenciálszámítás segítségével oldották meg, azonban bizonytalanul botladoztak a több határozatlan mennyiség között. Többnyire nem tudták indokolni, hogy miért differenciálnak az egyik szerint, a másikat állandónak tekintve. Egy versenyző volt, aki először is lecsökkentette a határozatlanok számát 1-re. Túl nagy fegyver azonban a feladathoz a függvénydiszkusszió módszere. Elegendő sokkal egyszerűbb algebrai tényeket használni fel.
 

Megoldás: Felhasználva a gyökök és együtthatók közti összefüggéseket és az együtthatók közt feltételezett kapcsolatot:
x1+x2=-ba,x1x2=-ca=-bcab=-a2ab=-ab.
Így az eggyel növelt gyökök szorzata
(1+x1)(1+x2)=1+(x1+x2)+x1x2=1-ba-ab==ab-b2-a2ab=-(a-b)2-abab=-1-(a-b)2ab.


Mivel a és b pozitív, ez mindig kisebb -1-nél, csak akkor egyenlő vele, ha a=b. Ekkor a2=bc=ac folytán a=c, tehát mindhárom együttható egyenlő, vagyis lényegében az
x2+x-1=0
egyenlettel van dolgunk.
 

3. Bizonyítandó, hogy bármely konvex négyszögnek van olyan csúcsa, melyből induló oldalakat paralellogrammává egészítve ki, e paralellogrammát a négyszög tartalmazza.
 

A feladat egy érdekes csapdát rejt magában, ami sok pályázót tévútra vezetett, még olyanokat is, akik lényegében jó megoldást találtak. A legnagyobb és legkisebb oldalból, vagy szögből igyekeztek kiindulni sokan, pedig ez nem lehet jellemző a feladat megoldására, hisz ha megrajzolunk egy négyszöget és bele a kérdéses paralellogrammát és az egészet csuklóval összeillesztett rudakból képzeljük, akkor ezt a szerkezetet tetszés szerint hajlíthatjuk. Legalább is amíg semelyik szög nem lépi át a 0 vagy 180∘-ot, addig tovább is tartalmazni fogja a négyszög a paralellogrammát, a kisebb-nagyobb szög viszonya azonban közben megváltozik. Ugyancsak nem változtat az ábra szerkezetén, ha tetszőleges irányban és mértékben megnyújtjuk, de megváltoztatható ezen a módon az oldalak nagyságviszonya. Más úton kell tehát a mogoldást keresni.
 

I. megoldás: Paralellogrammákra nincs mit bizonyítanunk. Ha a négyszögnek egy oldalpárja párhuzamos, (trapéz esetén) a rövidebb párhuzamos oldal bármelyik végpontjából húzhatunk párhuzamost a másik végpontból induló oldallal.
Az általános négyszög esetét a trapézére fogjuk visszavezetni. Ehhez olyan trapézt kell a négyszögből kivágnunk, melynek rövidebb párhuzamos oldala és egyik ezzel szomszédos oldala egybeesik egy-egy négyszögoldallal. Ekkor ez a két oldal egészíthető ki a kívánt paralellogrammává. Ilyen trapézt be tudunk rajzolni a négyszögbe. Keressük meg az egyik szemközti oldalpár metszéspontját és válasszuk ki a másik két oldal közül azt, amelyiknek végpontjai e metszésponthoz közelebb esnek. A negyedik oldalnak abból a végpontjából, amely a szemközti oldalhoz közelebb fekszik, húzzunk a szemközti oldallal párhuzamost. Így valóban a kívánt tulajdonságokkal rendelkező trapézt kaptunk.
 

II. megoldás: Paralellogramma és trapéz esetében ugyanúgy járhatunk el, mint az előző megoldásban.
Vizsgáljuk most meg, hogy egy szabálytalan négyszögben mivel jellemezhető egy oldalpár, mely a kívánt tulajdonságú paralellogrammává egészíthető ki. Tegyük fel, hogy az ABCD négyszög oldalai közt nincsenek párhuzamosak és az AD és DC oldal kiegészíthetők olyan paralellogrammává, melyet a négyszög tartalmaz.
Ekkor DCA∢≤CAB∢ és DAC∢≤ACB∢. Fordítva, ha egy átló az egyik oldalán fekvő mindkét oldallal kisebb, vagy legfeljebb akkora szöget zár be, mint az átellenes oldallal, akkor e két oldalt egészítve ki paralellogrammává, a párhuzamosok a négyszög belseje felé indulnak s így a paralellogrammát a négyszög tartalmazza. Azt kell tehát megmutatnunk, hogy az egyik átlónak mindig megvan ez a tulajdonsága.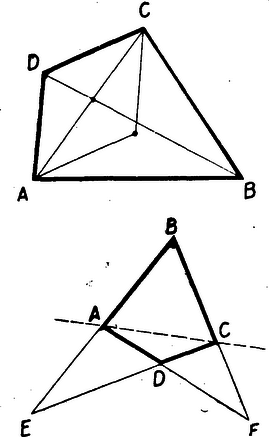
 
 

Legyen AC az az átló, amelynek ugyanarra az oldalára esik az átellenes oldalpárok E és F metszéspontja. Legyen D a másik átló azon végpontja, amelyik AC-nek ugyanazon oldalára esik, mint E és F.
Ekkor
ACB∢=CAF∢+CFA∢>CAF∢=CAD∢,
és
CAB∢=ACE∢+AEC∢>ACE∢=ACD∢,
tehát az AD és DC oldalak a kívánt tulajdonságú parallelogrammává egészíthetők ki.
 

III. megoldás: Az előző megoldásban láttuk, hogy elég azt megmutatni, hogy valamelyik átló az egyik oldalára eső egyik négyszögoldallal sem zár be nagyobb szöget, mint az illető oldallal szemközti oldallal.
Legyen az ABCD négyszög átlóinak metszéspontja E. Ha az AC átló bír a kívánt tulajdonsággal, akkor a mondottak szerint igaz az állítás. Ha nem, akkor feltehetjük, hogy pl.
BAC∢≤ACD∢,  de  BCA∢>CAD∢.
Ekkor
ABE∢+BAE∢=AED∢=CDE∢+DCE∢,
tehát a fenti első egyenlőtlenség következtében
ABE∢≥CDE∢.
Másrészt
ADE∢+DAE∢=AEB∢=BCE∢+CBE∢.
tehát a második föltételi egyenlet folytán
ADE∢>CBE∢.
Így a BD átló felel meg ez esetben a kívánt feltételnek. (A BCD törtvonal egészíthető ki a kívánt paralellogrammává.)
 

IV. megoldás: Két szomszédos oldalt úgy egészíthetünk ki paralellogrammává, hogy közös végpontjaikat tükrözzük a másik két végpont összekötő egyenesének (tehát a négyszög egyik átlójának) felezőpontjára. Mindegyik csúcsnak így megszerkesztjük a tükörképét és a bizonyítandó tétel azzal helyettesíthető, hogy a négyszög tartalmaz ezek közül legalább egyet.
Ha az átlók kölcsönösen felezik egymást, akkor a tükörképek az átellenes csúcsok, tehát mind a négyszöghöz tartoznak.
Ha pédául AC felezi BD-t, (de megfordítva nem), akkor AC-nek a metszésponthoz közelebbi végpontját tükrözve BD felezőpontjára nyilván a négyszögbe eső pontot kapunk.
Ha egyik átló sem felezi a másikat, akkor csak a metszésponthoz közelebbi végpontok tükörképe eshet a négyszögbe. Legyenek ezek a végpontok A és B, tükörképük a BD illetve AC átló középpontjára 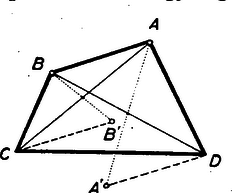A', illetve B'.
 
 

A' az AC és AD szárak közti szögtérbe esik, B' a BC és BD szárak köztibe. Így csak attól függ, hogy a négyszöghöz tartoznak-e vagy kívül esnek rajta, hogy a CD egyenes melyik oldalán vannak. Szerkesztés szerint A'D és B'C párhuzamos AB-vel. Így ha CD is párhuzamos AB-vel, akkor A' és B' is CD-re esik, ellenkező esetben pedig CD különböző oldalán feküsznek, tehát egyik a négyszögben, a másik rajta kívül. Ezzel állításunkat igazoltuk.
 

V. megoldás: Két oldal akkor egészíthető ki a kívánt tulajdonságú paralellogrammává, ha a nem közös végpontjaikból a másik oldallal párhuzamosan húzott egyenesek a négyszög belseje felé indulnak. Szemeljünk ki egy oldalt. Egyik végpontjából a másik végpontból induló oldallal párhuzamosan húzott egyenes akkor indul a négyszög belseje felé, ha a kiszemelt oldal melletti szögek összege legalább 180∘.
De a négyszög szögösszege 360∘ lévén, egy szemközti oldalpárból az egyik oldal mellett legalább 180∘-nyi szög kell hogy feküdjék. Mindkét szemközti oldalpárból kiválasztva az (vagy egy) ilyen oldalt föltétlenül szomszédos oldalpárt kapunk. Ezek kiegészíthetők teljesen a négyszöghöz tartozó paralellogrammává.