|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A körző csuklós műszer, amelyben két kar (szár) közös pontja, a körző sarka, csuklója körül elforgatható. Ha a saroktól a körző hegyéig a két szár hossza és , akkor a körzővel olyan és csak olyan köröket lehet rajzolni, amelyeknek sugara és között van, mert , és egy háromszög három oldala.
Bizonyos számú állandó hosszúságú kar, amelyeket bizonyos közös pontjaik, csuklók körül el lehet forgatni, csuklós szerkezetet alkot. Ebben a csuklók körül forgatható karok szöge változik.
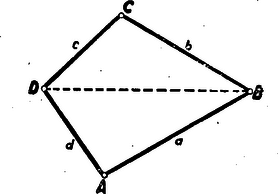
A körző után a csuklós négyszög a legegyszerűbb csuklós szerkezet. Az csuklós négyszög , , és hosszúságú karból, s ezeket a karokat az egy síkban fekvő , , és pontban egymáshoz kapcsoló , , és csuklóból áll. Mivel , , és egy négyszög négy oldala, azért a négy kar közül akármelyik kisebb, mint a többi három kar összege. Általános csuklós négyszögben a karok hossza különböző lehet és két szomszédos kar összege általában nem egyenlő a másik két kar összegével. A csuklós négyszög egyik szögétől, pl. a szögtől függ a többi szög, a két átló hossza és két különböző kar egy-egy pontjának távolsága.
Egy csuklós négyszöget a karok lehető elfordításával igen változatos alakokra lehet hozni. Ugyanaz a csuklós négyszög lehet egyszer konvex, máskor konkáv, harmadszor magát keresztező négyszög, sőt háromszög alakot is mutathat. Ez az utóbbi alak akkor fordul elő, ha két kar egy egyenesbe esik. Az csuklós négyszög alakjának változtatásakor az és kar csak akkor eshetik egymás meghosszabbításába , ha , és egy valóságos, vagy egyenes szakaszra elfajuló háromszög oldalai, ekkor , s az csukló a háromszög oldalára esik. Az és kart akkor fordíthatjuk egymásra , ha az esetben , és egy háromszög oldalai. Ekkor az csuklós négyszög alakja háromszög, amelynek oldalához folytatásként csatlakozik a szakasz.
Egy csuklós négyszög egyenes szakaszra fajul el, ha csuklói egy egyenesre kerülnek. Ez akkor fordulhat elő, ha két szomszédos kar együttes hossza a másik két kar együttes hosszával egyenlő, miként paralelogrammában és deltoidban. Deltoidalakú csuklós négyszögnek van L alakja is, amikor két csukló egymásra esik, s azokból kiinduló karok fedik egymást és egymásra merőlegesek.
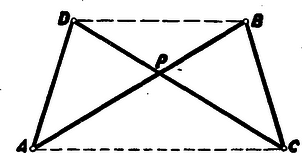
Az csuklós paralelogrammából származó keresztező négyszög, ellenparalelogramma karjának ( és csuklójának) rögzítésekor a csuklós négyszög többi három karjának elforgatása alatt a keresztezéspont és gyújtóponttal és hosszúságú főtengellyel bíró ellipszisen mozog.
 1. ábra.
Az és szemközt fekvő és egyenlő oldal metszéspontja -tól és -től egyenlő távolságra van, mivel az és háromszög egybevágósága miatt az háromszög alapján fekvő szögek egyenlők. Emiatt és A keresztezéspontnak ezt a tulajdonságát használta fel 1931-ben Yates R. amerikai matematikus ellipszisrajzoló készülékének elkészítésére. (Készülékét általánosabb görbék rajzolására szükséges alkatrészekkel is fölszerelte.)
Már a gőzgép felfedezője Watt is használt csuklós paralelogrammát, hogy a dugattyú mozgása a gőzhengerben lehetőleg egyenesvonalú legyen.
A csuklós négyszögnek egy olyan csuklóját, amelynek szöge és között minden szögértéken átmehet, teljes fordulású csukló-nak nevezzük.
Az csuklós paralelogramma mind a négy csuklója teljes fordulású. Ha az és csuklót annyira széthúzzuk, hogy és az szakaszra essék, akkor és . Ha pedig a és csukló széthúzásával és a szakaszra esik, akkor és . Amíg a csuklós paralelogramma egyik szélső (elfajult) alakjából a másikba átmegy, mindegyik szöge átmegy és között minden szögértéken.
Olyan csuklós négyszögre, amelyben a karok hossza különböző, a következő tételt mondhatjuk ki:
Egy olyan csuklós négyszögben, amelynek négy karja közül van egy legkisebb és egy legnagyobb, vagy két csukló teljes fordulású, vagy egy sem. Ha van a csuklós négyszögben teljes fordulású csukló, akkor az a két csukló ilyen, amelyet a legrövidebb kar köt össze. A legrövidebb karral összekapcsolt két csukló mindig teljes fordulású, ha a legrövidebb és a leghosszabb kar együttes hossza nagyobb, mint a másik két kar együttes hossza.
A tételnek két megoldását adjuk. Aki még trigonometriáról nem hallott, az az elsőt átugorhatja. Először azt vizsgáljuk, hogy az csuklós négyszög oldalainak , , , hosszából milyen következtetést lehet vonni az szögre.
Az háromszögben a cosinustétel szerint a háromszögben pedig (itt egyenlőség jele is állhat, mivel a , és pont egy egyenesre is eshet). Így -ra a következő egyenlőtlenségeket kapjuk:
Kérdés, milyen értékek közt változhat ? Milyen feltételek mellett érheti el a fenti határokat? A cosinus függvény és között egynél nem nagyobb számértékű minden valós értéket fölvesz, tehát minden olyan értéket, amelyre és , mert ekkor szükségképpen .
és
mindig teljesül, mert a négyszög bármely oldala kisebb, mint a többi háromszög összege.
Így ha akkor van olyan szög, amelyre , különben pedig nincsen. Ha nem az egyenlőségjel érvényes, akkor . Ez pedig egyértelmű azzal, hogy Ekkor , tehát .
Hasonlóan: ahhoz, hogy legyen olyan , amelyre , kell, hogy | |
legyen. Ekkor folytán , és , ha Ha az és egyenlőtlenség egyszerre teljesül, akkor .
Ha ellenben egyszerre fennáll az és az egyenlőtlenség is, akkor az szög és között minden értéket felvehet, mivel -nak és között nincs sem legkisebb, sem legnagyobb értéke. Ekkor az csukló teljes fordulású.
Számítás nélkül is könnyű bebizonyítani, hogy az és az egyenlőtlenség fennállása esetén teljes fordulású csukló, különben pedig nem az.
Föltételezhetjük, hogy . Vizsgáljuk ismét a átlót. A négyszög bármely helyzetében az -ből azt kapjuk, hogy a -ből pedig
Ezek szerint az kart akkor lehet az kar meghosszabbításába forgatni, ha és akkor lehet ráforgatni az karra, ha Ha valamelyik egyenlőtlenség helytelen, akkor a megfelelő forgatás sem hajtható végre. Tegyük fel, hogy , ekkor az utóbbi egyenlőtlenségben elhagyható az abszolútérték jele, mert a különbség pozitív, és az egyenlőtlenség így rendezhető: (2)-t és (3)-at összeadva Mivel feltettük, hogy és , így azt kaptuk, hogy a legrövidebb kar, a leghosszabb pedig vagy . Mindkét esetben a (2) és (3) azt mondja, hogy a legrövidebb és leghosszabb oldal együtt nem lehet hosszabb a másik kettő összegénél. Ekkor és csak is ekkor lehet az csúcs ‐ és az eredmény mutatja, hogy egyúttal a legrövidebb oldal másik végpontja a csúcs is ‐ teljes körülfordulású.
Ezek szerint a csuklós négyszögnek kétféle fajtája van, az egyik fajtának van teljes fordulású csuklója, a másiknak nincs. Az olyan csuklós négyszöget, amelynek nincs teljes fordulású csuklója, a karok forgatásával nem lehet úgy alakítani, hogy az egyik csuklóban a két kar szöge egyszer és máskor legyen. Mindig lehet azonban úgy alakítani, hogy egyszer valamelyik csuklóban a két kar szöge legyen és máskor pedig egy másik csuklóban a két kar szöge legyen.
Ha ugyanis semmikép sem lehetne az csuklós négyszöget úgy alakítani, hogy az , , és csuklóban a két kar , , , ill. szöge közül valamelyik legyen, akkor | |
volna, ahol
Ekkor azonban
és így
volna. Ez azonban lehetetlen, mert és között fekvő , , , szögre az utolsó egyenlet baloldalának mindegyik tagja pozitív.
Ha pedig , , , közül egy sem lehetne zérus a csuklós négyszögben, akkor volna olyan -nál nem nagyobb pozitív , , , szög, hogy
Ebből következik, hogy
Ez azonban szintén ellentmondás, mivel az egyenlet baloldalán mindegyik tag pozitív.
|
 PDF | MathML
PDF | MathML