Kezdőlap


Cím:	Síkgörbék fonalas szerkesztése 3.
Szerző(k):	Molnár József
Füzet:	1950/október, 176 - 179. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Folyóiratunk előző számában pozitív súlyú fókuszokkal rendelkező Tschirnhaus-féle görbékkel foglalkoztunk, vagyis olyan görbékkel, melyeken egy $P$ pontnak az $F_{1}$ , $F_{2}$ , $...$ , $F_{n}$ rögzített pontoktól való távolságait adott pozitív $q_{1}$ , $q_{2}$ , $...$ , $q_{n}$ állandókkal szorozva állandó $k$ összeget kapunk.

\begin{matrix} q_{1} P F_{1} + q_{2} P F_{2} + ... + q_{n} P F_{n} = k . \end{matrix}

A hiperbolában olyan görbét ismertünk meg, amelyet szintén hasonló egyenlet jellemez, de vegyes előjelű (

+ 1

- 1

) súlyokkal. A hiperbolára első cikkünkben ismertetett fonalas szerkesztést hasznosítani lehet általánosabb vegyes előjelű súlyokkal rendelkező Tschirnhaus-féle görbék fonalas szerkesztésére is.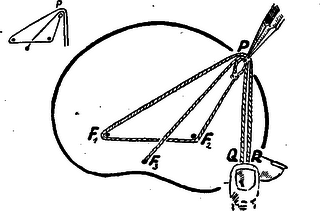

1. ábra.

Könnyen leolvasható az 1. ábráról pl. hogy a feltüntetett fonalmenet segítségével olyan görbét rajzolhatunk, melynek

F_{1}

F_{2}

F_{3}

a fókuszai és melyre nézve a

P F_{1} + P F_{2} - P F_{3}

kifejezés értéke állandó, vagyis egy

q_{1} = q_{2} = 1

q_{3} = - 1

súlyokkal rendelkező Tschirnhaus-féle görbét kapunk. A két fonalat más

Q

és

R

pontban fogva össze, az előbbivel azonos fókuszokkal rendelkező görbét kapunk, de az állandó értéke már más lesz. Az alábbi két ábra ilyen, ú. n. konfokális görbéket ábrázol. Az állandó igen nagy értékei esetén a görbe csaknem kör alakú. Kisebb állandókkal a görbe nemcsak köralakját veszítheti el, hanem konvexitását is. Az első görbeseregen látni, hogy ha az állandót úgy választjuk, hogy

P F_{1} + P F_{2} - P F_{3} = F_{1} F_{3} + F_{2} F_{3}

legyen, akkor a görbének

F_{3}

-ban szögpontja van. Azt is látni, hogy a görbe két különálló menetből is tevődhet össze. Az egyik menet egyetlen ponttá is zsugorodhat.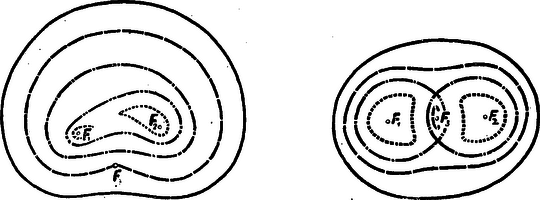

2. ábra. 3. ábra.

A második görbeseregben a negatív

F_{3}

fókusznak az

F_{1} F_{2}

szakasz felezési pontját választottuk. Itt látunk olyan görbét is, mely önmagát átmetszi, meg olyant is, melynek két menete közül az egyik a másik belsejében van. A belső menet itt is összezsugorodhat egy ponttá.
Ha a fókuszokat változtatjuk és

F_{3}

F_{2}

-be kerül, akkor a görbe

F_{1}

közepű körré változik; ugyanis mivel

P F_{2} = P F_{3}

, következik, hogy ekkor

P F_{1} + P F_{2} - P F_{3} = P F_{1}

marad állandó. Ha azonban

F_{1}

F_{2}

-vel esik össze, akkor ‐ az állandót

k

-val jelölve ‐

2 P F_{2} - P F_{3} = k

egyenlettel rendelkező Descartes-féle görbét kapunk.
Hasonlóan rajzolhatunk több fókusszal is vegyes előjelű súlyokkal rendelkező Tschirnhaus-féle görbéket.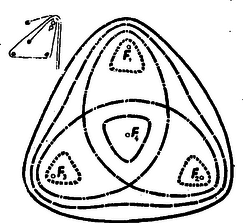

4. ábra.

A 4. ábra egy negatív és három pozitív fókusszal rendelkező konfokális görbesereget ábrázol. Az

F_{1}

F_{2}

F_{3}

pozitív fókuszok az

F_{4}

negatív fókusz körül szabályosan helyezkednek el. A görbék alakja itt is a három szimmetrikus fókusznál látottakhoz hasonló lehetőségeket mutat.
A fókuszokat változtatva, egy pozitív és egy negatív fókusz összeesésekor itt a görbe ellipszissé változik, három pozitív fókusz összeesésekor pedig Descartes-féle görbét kapunk.
A következő két ábra két pozitív és két negatív fókusszal rendelkező görbéket mutat. Az elsőnél egy rombusz szemközti csúcsaiban, a másodiknál egy téglalap két szomszédos csúcsában helyezkednek el az egyenlő előjelű súlyokhoz tartozó fókuszok. Az első esetben kapunk zárt és nyílt görbéket is, a második azonban már csupán nyílt görbéket szolgáltat.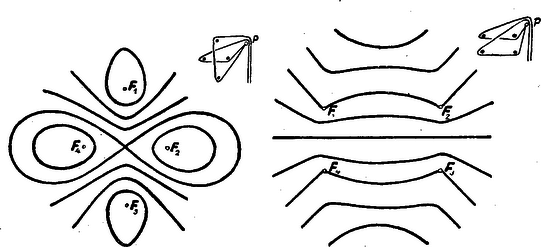

5. ábra. 6. ábra.

Gondoljunk vissza még egyszer a hiperbolára. Ott a fonalas szerkesztés a két ág közül ‐ amit pl. koordinátákkal tárgyalva egy összetartozó görbének ismertünk meg ‐ csak az egyiket szolgáltatja. A másikat akkor kapjuk, ha a súlyok előjelét ellenkezőre változtatjuk. A hiperbolához hasonlóan annak is van bizonyos alapja, hogy az olyan görbéket, melyek fókuszai és állandója egyenlő és a súlyok is csak előjelben különböznek egy görbe különböző meneteinek vagy ágainak tekintsük. Ezt különösen hihetővé teszi a következő két ábra.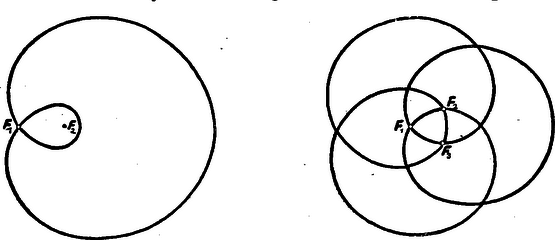

7. ábra. 8. ábra.

A 7. ábra a

P F_{1} + 2 P F_{2} = 2 F_{1} F_{2}

és

2 P F_{2} - P F_{1} = 2 F_{1} F_{2}

egyenlettel jellemzett görbéből tevődik össze. Az

F_{1}

pontban nemcsak találkozik a két görbe, hanem olyan szépen összesimul, hogy nehéz is két görbének látni. Pascal-féle csigavonal néven is ismeretes ez a görbe. Ez alkalmazást nyer különböző geometriai és fizikai problémákkal kapcsolatban.
Utolsó ábránkon négy görbe kapcsolódik egybe. Mindegyik fókuszai a szabályos háromszöget kitűző

F_{1}

F_{2}

F_{3}

pontok, az állandó értéke e háromszög oldalának kétszerese, s azok a görbék vannak megrajzolva, melyek csupa

+ 1

súlyhoz és melyek egy

- 1

, és két

+ 1

súlyhoz tartoznak.