Cím: Síkgeometriai tételek bizonyítása térgeometriai meggondolások közvetítésével
Szerző(k):  Kárteszi Ferenc 
Füzet: 1950/május, 109 - 117. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Síkgeometriai tételek bizonyítása térgeometriai meggondolások közvetítésével

(Sztereografikus projekció.)
 

A körsorokról szóló közleményemben arra törekedtem, hogy lehetőleg ne vegyek igénybe aritmetikai segédeszközöket. Mégis volt benne két ,,számításos'' részlet és éppen ezeken épült fel az egész közlemény tartalma. A következő két tétel bizonyításában alkalmaztunk aritmetikai meggondolást.
(α) Ha a k és l körök közös pontja A és B, akkor az AB egyenesnek a két körön kívül eső bármely pontjából a két körhöz összesen négy egyenlő érintő írható.
(β) Ha három kör páronként metsző, a párok meghatározta három hatványvonal egy pontban találkozik. (A belső hatványpont esetében aritmetika meggondolást alkalmaztunk.)
Ha (α) és (β) tételt sikerülne az aritmetika alkalmazása nélkül bebizonyítani, akkor az egész közlemény tiszta geometriai úton lenne tárgyalható.
No most megmutatom, hogy térbeli meggondolások segítségével, miképpen lehet ezt a két kényes tételt ,,számítás'' nélkül bebizonyítani.
 

I.

 

Toljunk a H forgáshengerbe egy vele megegyező átmérőjű G gömböt. A gömb egy k főköre mentén érinti a hengert. E kör síkja α, merőlegesen áll a henger t tengelyére. Ha a k körrel határolt felső félgömböt merőlegesen vetítjük az α síkra, egyrétű képet nyerünk, mely megtölti a k kör belsejét. A k kör a kép kontúrja.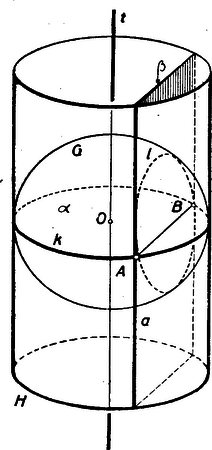
 
1. ábra.
 

Vágjuk át a hengert és a gömböt egy a t tengellyel párhuzamos β síkkal. Ez a hengert a és b alkotóban, a gömböt l körben metszi. Az α síkot pedig a k kör AB húrjában.
Könnyen belátható, hogy az l kör a sík fölötti felének a síkra eső merőleges vetülete éppen az AB húr, s ez az egyenes szakasz a szóbanforgó félkörnek egyrétű képe.
E szerint a rajzlapra írt k kör belseje és húrja mindég úgy tekinthető, mint a k ereszvonal fölé épített félgömb kupola és a kupolára írt a rajzlapra merőleges síkban fekvő félkör merőleges vetülete (képe).
Nyilvánvaló, hogy a k és l kör A-hoz tartozó érintője két egymásra merőleges egyenes. (Az első vízszintes síkban van, a másik pedig éppen a függőleges a alkotó.)
Képzeljük el külön a k és l kört, mint egy-egy körlemezt úgy, amint a térben állnak, továbbá hosszabbítsuk meg a lemezek metszésvonalát, ez a h egyenes.
A h tetszőleges külső pontjából írjunk egy-egy érintőt a két körhöz. HK az egyik, HL a másik érintő.
 
2. ábra.
 

Minthogy ezek a felső félgömbnek H-ból írt érintői, nyilván egyenlők. Hiszen egy pontból a gömbhöz írt érintők mind egyenlők, mert egy forgáskúp alkotói. Ez a kúp egy gömbi kis kör mentén érinti a gömböt. (Könnyen belátható, tessék csak egy pontból két érintőt írni egy körhöz az így nyert ábrát a szimmetriatengelye körül forgatni!)
No most képzeljünk el egy síkban két kört, k1-t és k2-t, de úgy hogy A, B pontokban messék egymást. Forgassuk az ábrát a szimmetriatengelye körül. Két gömb keletkezik, amelyeknek a metszésvonalát az A is meg a B is leírja forgás közben. Tehát a két gömb egy gömbi kis körben, l-ben metszi egymást.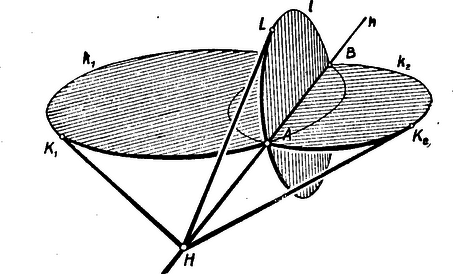
 
3. ábra.
 

Az ábra k1, k2, és l köre a G1, G2 félgömböt határoló köröket és a metszési körüket szemlélteti. A G1 gömbre gondolva, HK1 és HL egyenlő; a G2 gömbre gondolva, HK2, és HL egyenlő. Tehát HK1=HK2.
Ha a k1 és k2 körök alkotta síkbeli ábrát értelmezzük, tekinthetjük két félgömb-kupola ereszvonalának. A közös AB húr pedig a két félgömb-kupola metszésvonalának képe. Vagyis a síkbeli ábra a térbeli alakzat képe.
 
4. ábra.
 

A 3. ábrával egybevetve nyilvánvaló, hogy a két kör létesítette h vonal külső H pontjából írt HK1 és HK2 érintők egyenlők. Ezzel az (α) tételt ,,számolás'' nélkül igazoltuk.
Az 5. ábrát tekintsük három félgömb-kupola merőleges képének, ahol rendre a k1, k2, k3 a három kupola ereszvonala. Legyen a G1, G2; G2, G3; G3, G1 kupolapárok metszésvonala rendre az l12, l23, l31. Az első két metszésvonalnak h12 és h23 a képe. Az első két metszésvonal mindketteje a G2 gömbre van írva, kereszteződő állásban, metszéspontjuknak az M a képe.
 
5. ábra.
 

Ez a metszéspont, amint az 12 és 23 index is mutatja, mind a három gömbön rajta van, tehát az l31 metszésvonalnak is pontja. Az l31 vonal képe pedig az AB húr, ezért az AB húrnak is át kell mennie az M képen. Ezzel pedig éppen a (β) tétel ,,számítás nélküli'' bizonyítását, nyertük.
 

II.

 

Most más, látszólag gyakorlati kérdésre térek át. A probléma a következő. Tessék a földgömböt síkon ábrázolni (Más szóval: tessék a földgömbről síkra vetett térképet rajzolni.) A végén majd kiderül, hogy a felvetett kérdéssel való foglalkozás geometriai ismereteink szempontjából is lényeges gyarapodást jelent. A gömbi térkép termékeny, új geometriai szemléleti módot fejleszt ki.
Nyilvánvaló, hogy az ábrázolás módját, a térkép gyakorlati céljához kell szabnunk. Olyan térkép szükséges, amelyen a földrajzi hálózat (a hosszúsági és szélességi körök hálózata) jól tájékoztat és a fokmérést a térképen egyszerű módon végezhetjük. A földrajzi hálózat ,,ablakokra'' tagolja a térképet, s ha jó sűrű, akkor könnyű a felszíntagozódást ablakról-ablakra haladva belerajzolni. Tehát a földgömb térképén lényeges kérdés a földrajzi hálózat ábrázolása.
Könnyű dolgunk lenne, ha a föld felszín hengerfelület volna. Ugyanis a hengeren a földrajzi hálózat egyszerű; egyenletes sűrűséggel elrendezett alkotók és egyenletes sűrűséggel elrendezett köröket választhatnánk hálózati vonalak gyanánt. Persze a hengeres térképet is síkra kellene rajzolni. E végből a 0 számozású alkotója mentén felvágjuk a hengert és síkba terítjük. A kiterítésben a körök is kiegyenesednek és a síkra rajzolt szalagtérképen olyan hálózati vonalrendszert nyerünk, mint ,,a kockás'' papiros két egymásra merőleges vonalserege.
No de a gömb nem teríthető ki síkba. Ezért a leírt módszert a gömb esetében nem alkalmazhatjuk. Vegyük talán a gömb vetületét térkép gyanánt? Sajnos a vetületben a hálózatikörök általában nehezen rajzolható vonalakká torzulnak, torzul a hosszúság, a szög, és a Föld egész felszínrajza.
Mégis a vetítés ötletéhez ragaszkodunk. Igyekezzünk azonban a vetítést olyan módon berendezni, hogy a térkép torzítása a valóságos terepviszonyokra való visszakövetkeztetésben a lehető legkisebb nehézséget akozza.
A térképpel szemben támasztott lényeges követeléseink a következők.
A földgömbre írt hálózati körök képe kör legyen, (mind a hosszúsági, mind a szélességi körök képe). Ha ez sikerül, a térkép hálózati vonalai körzővel megrajzolhatók. Az ilyen jellegű térképet körtartó térképnek nevezzük.
Ha a Föld méreteihez képest kicsi felületrészt ragadunk ki, a valóságos felszínforma és a neki megfelelő térképrajz legyen hasonló. Ezt a kicsinyben való hasonlóságot úgy szokták mondani, hogy a térkép konformis.
Az utóbbi kikötést most pontosabban értelmezzük. A kép és a földfelszín kicsiny ablakainak a hasonlósága azon alapszik, hogy a térképen szereplő szögek és a nekik megfelelő térképvonalak alkotta szögek egyenlők. Vagyis ha a', b' a térkép két egymást metsző vonala és a, b a földfelszínen nekik megfelelő vonalak, akkor
(ab)∢=(a'b')∢
legyen. Ezt a követelményt teljesítő térképet szögtartó térképnek nevezzük. A körtartó és egyben szögtartó térkép létesítésére alkalmas vetítési mód feltalálása nehéz feladatnak látszik.
Az alkalmas vetítési mód feltalálását Hipparchos-nak köszönhetjük. A G gömb egy átellenes pontpárját jelöljük E és D-vel. Jelöljük δ-val a gömb érintő síkját a D pontban. (A δ a további szövegben is ezt az érintő síkot fogja jelölni.) Az E világító középpontból vetítsük az átlátszónak képzelt gömbhéj felszínrajzát a δ képsíkra. Az így származtatott vetületet sztereográfikus képnek nevezzük.
 

III.

 

A sztereográfikus vetület szabatos geometriai tárgyalásához most egy modellre volna szükségünk. Kénytelen vagyok ábrával és hozzáfűzött értelmező szöveggel pótolni a modellt.
 
6. ábra.
 

A 6. ábra a következő viszonyokat szemlélteti. A G gömb E, D átellenes pont párját f függőleges tengely (átmérő) köti össze. Az α sík merőlegesen áll az f tengelyre, azaz vízszintes. Az f tengely talppontja az O'=D' pont. Az x és y egyenes az X pontban érinti a gömböt, tehát az OX sugárra merőlegesek. Az x egyenes az N az y egyenes az M pontban metszi az α síkot. Az EX=s egyenes (az X pont vetítősugara az E vetítési középpontra nézve) az X' pontban metszi az α síkot. Tehát ha az E pontból vetítjük az x és y érintő egyeneseket, az NX'=x' és MX'=y' lesz a képük.
Ha az u és v egyenest az E pontból az x' és y' egyenessel párhuzamosan vezetjük, vízszintes állásúak lévén, a gömb két érintő egyenesét nyerjük. Az u-nak metszenie kell az x-t, mart az u, x' párhuzamos egyenespárt összekötő sík tartalmazza az s egyenest és vele együtt az X pontot. Ezért az NX-nek metszenie kell az u egyenest. Hasonlóképpen v-nek metszenie kell az y-t. U és V jelöli a szóbanforgó metszéspontokat. Az U pontból a gömbhöz írt UE és UX érintők egyenlők. Más szóval az UEX egyenlőszárú háromszög. Az u és x' párhuzamossága folytán az NXX'Δ hozzá hasonló, tehát egyenlőszárú háromszög, NX=NX'. Hasonlóképpen MX=MX'. Ebből már az is nyilvánvaló, hogy a NX'MΔ és NXMΔ egybevágó háromszögek, hiszen az MN oldaluk közös. Így az X-nél és az X'-nél levő szögük megegyezik:
(xy)∢=(x'y')∢.

Kénytelen voltam a további mondanivalóim miatt ezt a hosszú magyarázatot fűzni a modellt pótló 6. ábrához.
Lássuk csak, miféle összefüggéseket olvashatunk ki ebből az ábrából?
(I.) Ha az f tengely E döféspontjából a reá merőleges síkra vetítjük a gömb érintőjét, akkor a vetület örökli az érintő hosszát. (Az érintő hosszán az érintőnek az érintési pont és a képsík közé eső szakaszát értjük)
(II.) A szóban forgó vetület a gömbi szöget örökli. (Ez a fentírt szögegyenlőség szóbafűzése.)
Ha az α síkot, állandóan az f-re merőleges állásban tartva, a D pontig emeljük, akkor éppen a δ sztereografikus, érintő képsíkot nyerjük. Az x' és y' helyébe a velük nyilván párhuzamos x* és y* lép, s így az ezek bezárta szög sem változik. Tehát az E-ből a δ-ra való vetület is szögtartó.
No most tessék az N pontot rögzíteni az α síkon. Mozgassuk a fix N ponton átmenő x egyenest úgy, hogy állandóan érintse a gömböt. Akkor az X érintési pont egy gömbi kis kört ír le ‐ ez a k ‐ és az N-től mért távolságát állandóan megtartja. Ez a távolság az N csúcsból a gömbhöz írt érintő-kúp alkotója. Persze a változó X pont képe, az x' is mozog az α síkon. Mit ír le a változó képpont? Egy az N középpont köré írt kört. Ugyanis a képpontnak az N-től való távolsága mindig ugyanakkora, mint a neki megfelelő gömbi pontnak az N-től való távolsága, ami pedig állandó. Tehát az N pontból a gömbhöz írt kúp érintési körének az E-ből az α-ra való vetülete olyan kör, melynek a kúp csúcsa a középpontja és a sugara a kúp alkotójával egyenlő.
Ha az α helyett a vele párhuzamos δ sztereografikus képsík fogja fel a vetületet, akkor a szóbanforgó vetületnek ugyancsak körnek kell lennie (mert a kúp síkmetszetei hasonlók és itt a vetítősugarak kúpot alkotnak).
Minthogy minden gömbi kör előállítható egy külső csúcsból a gömbhöz írt érintő kúp érintési vonala gyanánt, a főkörök kivételével, belátható, hogy a G-re írt köröket E-ből a δ érintősíkra vetítve, a vetület is kör.
Kivételesen viselkednek az E ponton átmenő körök. Mert e körhöz tartozó vetítő sugarak egy síkba esnek, közönséges sugársort alkotván. A sugársor síkja egyenesben metszi a sztereográfikus képsíkot és ez az egyenes a kivételes helyzetű kör egyrétű, sztereografikus képe.
Modellünk segítségével bebizonyítottuk tehát, hogy a sztereografikus vetület körtartó és szögtartó. E szerint a gömb köreihez a képsík köreit (esetleg egyeneseit) rendeltük.
Megfordítva is igaz a dolog. A sík tetszőleges körének, vagy egyenesének egy olyan kör felel meg a gömbön, amelynek a képe éppen a sík szóbanforgó köre, vagy egyenese.
 

197. feladat. Bebizonyítandó, hogy a δ sík tetszőleges körét az E ponttal összekötő kúp körben metszi a G gömböt.
 

198. feladat. Bizonyítandó, hogy a G gömb legnagyobb köreinek (főköreinek) a sztereografikus képe is kör, ha a főkör nem megy át az E ponton.
 

IV.

 

A gömbre írt körök összefüggéseit tanulmányozó geometriai fejezetet gömbi geometriának nevezzük. A síkra írt körök összefüggéseit tanulmányozó kérdéskört pedig körgeometriának. (Megjegyzem, hogy a körgeometriában az egyenest is körnek tekintjük. Erre az ,,egy kalap alá'' vonásra az nyújt alapot, hogy mindkettő önmagában eltolható vonal, és a körön és az egyenesen kívül ezzel a tulajdonsággal más, síkra rajzolható vonal nem rendelkezik.)
A sztereografikus projekció közvetítésével a gömbi geometria és a körgeometria szoros rokonságba kerül. Ugyanis minden olyan tétel, ami a gömbi körökre nézve a szög fogalmával kifejezhető, illetőleg minden olyan tétel, mely a sík önmagában eltolható vonalainak szögekkel kifejezhető kapcsolatáról szól a sztereográfikus vetítés közvetítésével, egymásba átjátszható.
A gömbön való tükrözést pl. a következőképpen szokás érteni. Legyen a G gömb egy főköre az e kör és a gömb egy tetszőleges pontja P. P-ből az e síkjára állított merőleges egyenes másodízben P'-ben metszi a gömböt. Ez a pont a P-nek a gömbi tükörképe. No most kerüljük meg ennek a leírásnak az alkalmatlan motívumait és fogalmazzuk át a tükrözést úgy, hogy a leírásban csak a kör és a szög fogalmát alkalmazzuk. Mindazok a körök, amelyek a P és P' pontokon átmennek az e főkör síkjára merőleges síkokban vannak. E körök mindegyikét derékszögben metszi és felezi az e főkör.
A gömbön való tükrözést ezzel definiálhatjuk is: Mindazok a körök, amelyek a gömb felszínére úgy vannak írva, hogy átmennek az adott P ponton és az e kört derékszögben metszik, még egy pontban találkoznak, s ez a pont a P-nek az e-re való tükörképe.
 

199. feladat. Bebizonyítandó, hogy a gömbön való tükrözés műveletének sztereográfikus képe a síkon, körre való tükrözés (inverzió).
 

A sztereográfikus leképezés új szemléleti módra nevel bennünket. Ebben a szemléleti módban a gömbi geometria és a körgeometria bizonyos tételei és fogalmai dualitásba kerülnek (párokban jelentkeznek). Elegendő, ha a tételpár egyik tagját bebizonyítjuk, a másik tagja már nem szorul bizonyításra, mert az egyikből, a sztereográfikus vetítés közvetítésével, eleve tudjuk, hogy a másik tétel igazsága is gépiesen kikövetkeztethető. Tréfásan úgy mondhatjuk: ,,két legyet egy csapásra''.
 

200. feladat. A Föld egyenlítőjének és a 0-ik hosszúsági körének a metszéspontjából vetítsük a földrajzi hálózatot az átellenes pont érintő síkjára. Megrajzolandó a földrajzi hálózat képe, ha a köröket csak 30 fokonként tüntetjük fel. (Rajzot kérünk és a készítés leírását.)