Cím: A körsorokról 1.
Szerző(k):  Kárteszi Ferenc 
Füzet: 1950/február, 14 - 22. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I.
 

Részben ismeretes tételeket tárgyalok a következőkben. Síkgeometriai összefüggéseket tárgyalok, s az okoskodásokból igyekezem minimálisra, zsugorítani az aritmetikai ízű meggondolásokat.
Legyen adott a k kör és a külső, vagy belső P pont. Vegyük P ponton át azt a szelőt, mely a kör középpontján megy át és legtávolabb eső pontja, a rövid PU és hosszú PV szelvényt létesíti. Bármelyik irányban forgatjuk a szelőt P pont körív, a hosszú szelő egyre rövidebb, a rövid egyre hosszabb lesz, sőt egy pillanatban PX és PY egyenlővé válik. Belső pontra nézve a PO egyenesre merőleges állásban következik be az egyenlőség: 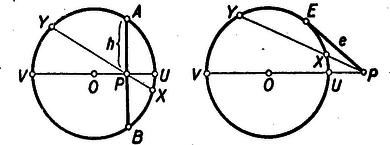PA=PB.
 
 
1. ábra
 

Külső pontra nézve pedig az érintkezés pillanatában: PE=PE. Jelölje PA, ill. PE távolságot röviden h, ill, e. Bár a forgás közben a rövid szelvény növekedett, a hosszú meg fogyott, a szorzatuk állandó maradt. Mégpedig, bizonyára, már tanultátok,
PX⋅PY=h2,ill.PX⋅PY=e2.(1)

A belső, illetőleg külső pontra vonatkozó h2, ill. e2 mennyiséget a pont körre vonatkozó hatványának nevezzük. A szelő rövid és hosszú szelvénye szorzatának az állandóságát, az (1.) alatti egyenleteket, hasonlósági következtetések révén tanultátok bizonyítani. (Tudniillik PAY∼PXB, PEY∼PXE hasonló háromszögek).
 

II.

 

Két kör közös húrjának nevezetes tulajdonságát találjuk a pont hatványának fogalma révén.
A 2. ábrán P pontot az AB húr egyenesén tetszőlegesen választottuk.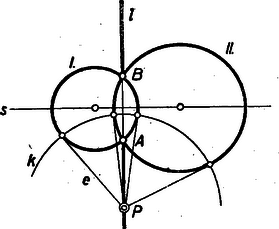
 
 
2. ábra
 
P pontból akár az I, akár a II körhöz írt érintő egyenlő PA⋅PB-vel, mert PA és PB szelvényeket akár az egyik, akár a másik körhöz viszonyítva tekinthetjük. P-ből a két körhöz négy egyenlő érintő ágazik. Az érintési pontok P középpont köré a PA⋅PB sugárral írt k körön sorakoznak.
Ha P pont mozog az l egyenesen, a k kör is változik. Ha az A pont felé tart, a kör ponttá zsugorodik; ha távolodik A-tól, a kör az s egyenesé tágul. (Ha az AB belső szakaszon van a P pont, akkor nem ágazik ki belőle a körökhöz érintő, tehát nincs hozzátartozó k kör sem). Mozgás közben P pontnak a hatványa állandóan változik, de az I körre és II körre vonatkozó hatványa egymás között állandóan egyenlő marad, még akkor is, ha P belső pontja a két körnek. Ezért az, l egyenest a két kör hatványvonalának nevezzük.
Ha P pont lelép az egyenesről, más lesz a hatványa I körre, mint II. körre nézve. (Ha l-ről jobbra lelép a mi ábránkon, akkor az I-re vonatkozó hatványa a II-re vonatkozónál nagyobbá válik). Bizonyítsátok be, hogy ez így van! 1. feladat.)
Most pedig az egymást metsző görbék hajlásszögének a forgalmát értelmezzük. Ennek a fogalomnak a bevezetése a hatványvonal fogalmának hasznos átfogalmazásához vezet.
Két görbe, g1 és g2 messe egymást az M pontban. Legyen e1 és e2 az érintőjük ebben a pontban. Nevezzük el az e1, e2 egyenesek hajlásszögét a görbék M pontban alkotott hajlásszögének. Ha a két egyenes merőleges egymásra, azt mondjuk, hogy a két görbe merőleges egymásra az M pontban. Ha a kör és b kör merőlegesek egymásra az M-ben, bármelyikük M pontbeli érintője a másiknak a középpontján megy át.
Pillantsatok vissza a 2. ábra k körére. Tüstént megértitek, hogy k kör az I, II köröket derékszögben metszi. Sőt az A B pontokat összekötő végtelen sok kör bármelyikét derékszögben metszi. (Ugyanis II kör helyett vegyük a végtelen sok kör bármelyikét, de tartsuk meg az I kört). Így a két kör hatványvonalát olyan módon is értelmezhetjük, mint az őket derékszögben metsző körök középpontjának geometriai helyét.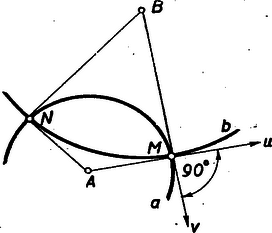
 
 
3. ábra
 

Sőt ezáltal tágítható a hatványvonal fogalma, az egymást nem metsző körök esetére nézve is. Az egymást nem metsző körökhöz mindig található alkalmas k kör, mely mind a kettőt metszi, Az AB és CD egyenesek közös P pontjából h-hoz érintőt írunk, ennek a hossza 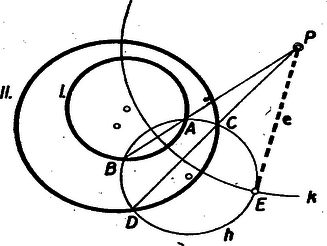PE=e.
 
 
4. ábra
 

Az I, k körpárra tüstént érthető, hogy P-ből e-vel egyenlő érintőpár ágazik az I-hez. A II, k körpárra nézve pedig az, hogy P-ből a II-höz ágazik két érintő, amelyek akkorák mint e. Eszerint P köré e sugárral írt k kör derékszögben metszi mind az I, mind a II kört. Tehát az így nyert P pont az I, II pár hatványvonalának egy pontja. Bebizonyítjuk, hogy a hatványvonal ebben az esetben is a két kör közös szimmetria tengelyére merőleges egyenes.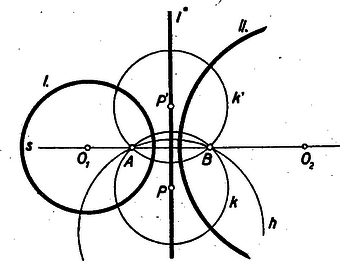
 
 
5. ábra
 

Legyen P az előbb mutatott eljárás szerint szerkesztett pont és k a köréírt, derékszögű kör az I, II-höz képest. Tükrözzük a k kört s egyenesre. Az így nyert, k' kör szintén derékszögben metszi I és II kört.
Minthogy pl. I a k ,k' körpárt derékszögben metszi, az A, B pontokon átmenő körsor mindegyik körét derékszögben metszi. Ugyanez áll II-re is. Tehát az A, B pontokon átmenő körök mind derékszögűek az I és II-höz, vagyis a szóbanforgó körsor középpontjait sorakoztató l egyenes, az AB felező merőlegese, az I és II kör hatványvonala.
Érintkező körök hatványvonala pedig nyilvánvalóan a közös pontjukhoz tartozó közös érintőjük.
 

III.

 

Három kör, I, II, III három párt értelmez: (I, II); (II, III); (III, I). A három pár pedig három hatványvonalat: a 12-, 23-, 31-et. Ez a három egyenes egy P pontban, a három kör hatványpontjában találkozik (6. ábra).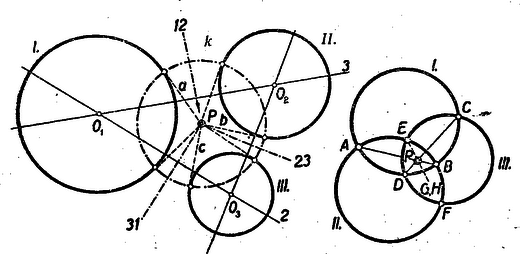
 
 
6. ábra
 

Azért nevezzük hatványpontnak, mert ennek a pontnak mind a három körre vonatkozó hatványa ugyanaz. Ha P külső pont, akkor a belőle kiágazó hat érintő egyenlő. Érintési pontjuk a P középpont köré írt k körön sorakozik. Ez a kör az I, II, III köröket merőlegesen metszi.
A tétel bizonyításához a 6. ábra első képe szemlélteti a viszonyokat. Egymást nem metsző körök esete. Jelölje P a 23 és 31 hatványvonalak metszéspontját, Akkor P-ből két-két egyenlő érintő ágazik a három körhöz, hosszúságukat jelölje rendre a, b, c. A 23 egyenes II és III körök hatványvonala, ezért b=c. A 31 egyenes a III és I köröké, ezért c=a. Tehát c=b is igaz, amiből éppen az következik, hogy a harmadik hatványvonal, az 1 2 is tartalmazza a P pontot.
Ugyanezzel a meggondolással a körök bármely kölcsönös helyzetének esetében megy a bizonyítás, csak arra az egy esetre, nem, ha a körök bármely ketteje metszi egymást és a közös húrok metszéspontja a körök belsejében van. Tudniillik a tétel ebben a kiemelt esetben is igaz, de a P ekkor a körök közös húrjainak metszéspontja, s így mind a három körre nézve belső pont. Nem ágazik belőle a körökhöz érintő és nem írható köré a három kört merőlegesen metsző kör. Csak az érvényes ebben az esetben is, hogy mind a három körre nézve P pontnak a hatványa ugyanakkora.
Ennek az esetnek a szemléltetésére való a 6. ábra másik képe. Az AB és CD közös pontját jelölje P. Kössük E pontot össze a P-vel. Nem hisszük, hogy ez az egyenes az F ponton is átmegy. (Ha elhinnők, nem szorulna bizonyításra). Tehát EP két különböző pontban metszi a II és III kört, jelöljük ezeket G- és H-val.
A PA, PB és PC, PD szelvények az I körben vannak és így az I.-ben mondottak szerint
PA⋅PB=PC⋅PD.
Hasonlóképen a II körből
PA⋅PB=PE⋅PG
és a III körből
PC⋅PD=PE⋅PH.
E három egyenlőség alapján
PE⋅PG=PE⋅PH,azazPG=PH.
Ez csak úgy lehetséges, hogy G és H ugyanaz a pont. Ámde EP egyenes a II és III kört csak akkor metszheti egybeeső pontokban másodszor is, ha éppen az F ponton megy át. Ezt nem akartuk hinni, de most már beláttuk, hogy igaz.
 

IV.

 

Ismeritek a. körsor elnevezést, tanultátok, hogy két ponton át számtalan kör írható, ezeknek az összességét nevezzük körsornak.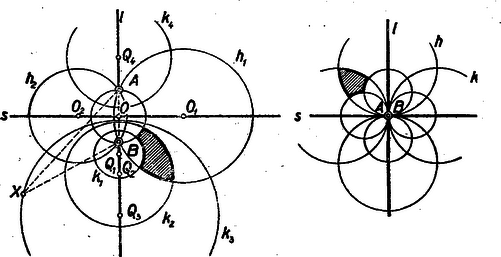
 
 
7. ábra
 

Az A, B pontokon át írható körsor tengelye az AB egyenes felezőmerőlegese, az s, hatványvonala az A és B pontot összekötő l egyenes, alappontjai az A és B pont. A körsor legkisebb körének AB az átmérője. Végtelen nagy köre is van, mert az s tengelyen a kör középpontja akár jobbra, akár balra távolodik a hn kör, az l egyenessé tágul.
Most új fogalmat vezetünk be, az A és B pontokhoz tartozó Apollonius-féle körsort. Az elnevezést megvilágítom egy bizonyításra kitűzött feladat révén. Ismeritek a következő tételt. Ha λ előírt aránymutató és A, B megadott pontok, akkor az
AX:BX=λ
kirovást teljesítő X pontok geometriai helye kör. Az A és B ponthoz tartozó, λ aránymutatójú Apollonius kör.
Bizonyítsátok be, hogy az A es B pontokon át írható kör sort derékszögben metsző k kör az A, B pontokhoz tartozó egyik Apollonius kör. (2. feladat.)
Az s tengelyt, A és B alappontokon átmenő körsort derékszögben metsző (k) körök összességét az A, B pontokhoz tartozó Apollonius-féle körsornak nevezzük. Van két ponttá zsugorodott köre: A és B nullkör. Van egyenessé tágult köre: ez az s egyenes. A körsor tengelye az l egyenes és hatványvonala az s egyenes.
A két ponton át írható körsor köreinek megrajzolása egyszerű rajzi munka. Az A, B pontokhoz tartozó Apollonius-féle körsor köreinek megrajzolásához megadható-e egyszerű rajzi utasítás? Igen. Legyen az AB átmérőhöz tartozó kör h és az átmérő egyenese l. Az l egyenes tetszőleges Q pontja, mint középpont, s a belőle h-hoz vezetett érintő, mint sugár meghatároz egy kn kört.
Az ábra s és l tengelyű körsora derékszögű körhálózatot alkot. (Bármely h kör bármely k kört derékszögben metsz). A kiragadott sötét idom derékszögű körnégyszög. Oldalai körívek, szögei derékszögek. Ha a körnégyszöget sűrűn rajzolt hálózatból vesszük, midőn oldalainak mérete AB távolsághoz képest elenyészően kicsinyek, a sötét parcella ,,majdnem'' téglalap.
Ha A és B egybeesik, mindkét körsor egy pontban érintkező körökből áll. Egyik sor a másikból az A=B pont körül való negyedfordulattal is származtatható. A 7. ábra második képe szemlélteti ezt a két különös körsort.
Könnyen belátható, hogy a sík bármelyik U pontján egy h és egy k kör megy át, azaz A és B kivételével minden pont egy s és l rendszerhez tartozó kör metszéspontjának tekinthető. (Bizonyítsátok be! 3. feladat.)
A derékszögű körhálózat fontos szerepet játszik a térképészetben. A térképen látható hosszúsági- és szélességi körök, ilyen hálózatot alkotnak, az északi- és déli-sarkpont tölti be az A és B alappont szerepét.
 

V.

 

Még egy fogalmat vezetünk be. A körre vonatkozó tükrözés fogalmát. Az egyenesre való tükrözés fogalmának tágításával nyerjük.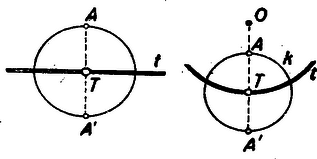
 
 
8. ábra
 

A fogalom tágításának egyik módját szemlélteti az ábra. A' pont A-nak a tükörképe t-re nézve. A második képen t szerepét egy kör, a reá bocsátott menőleges szerepét e kör egy sugara tölti be.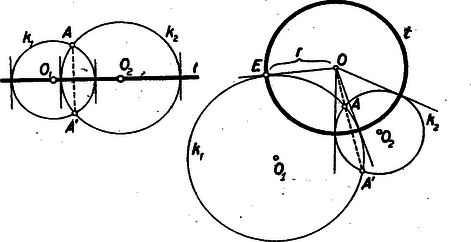
 
 
9. ábra
 

A fogalom tágításának egy másfajta módját szemlélteti a 9. ábra. Szerkesszétek meg A pont t egyenesre való tükörképét. Az egyenes egy-egy tetszőleges pontja köré kört írunk, mely A ponton megy át. A' két kör másik közös pontja az A' tükörkép. Ne felejtsétek el, hogy k1 és k2 merőlegesen metszi a t egyenest. Erre építjük a fogalom tágítását.
Vegye át t szerepét egy kör. Két hozzá derékszögű kör k1 és k2 az A és A' pontban metszi egymást. Most ezt a geometriai műveletet nevezzük el a körre vonatkozó tükrözésnek; A' az A-nak t körre vonatkozó tükörképe. Ha a kör sugara r, akkor pl, a k1 körre a szelők tételét alkalmazva
OA⋅OA=r2.
Visszatekintve a 7. ábrára, ebben az értelemben mondhatjuk. hogy az A és B pontok, a hozzájuk tartozó Apollonius-körök bármelyikére nézve, egymásnak tükörképe.
Kitűzött feladatok:
4. ‐ Legyen 1, 2, 3, 4, 5, 6 hat pont jele. Az 12, 34 és 56 találkozzék egy pontban. Ha 1 2 3 4 és 3 4 5 6 pontok egy-egy húrnégyszög csúcsai, bizonyítsátok be, hogy 5 6 1 2 is húrnégyszöget tűz ki.
Ez a térben is igaz, sőt a térben azt is hozzátehetjük. hogy a hat pont kőré gömb írható.
5. ‐ Adva van k kör és A, B pontok. Szerkesztendő az A, B pontokon átmenő kör, mely a k kört érinti.
6. ‐ Adva van ismét k és A, B. Szerkesztendő az A, B pontokon átmenő kör, mely a k kört derékszögben metszi.
7. ‐ Tekintsük egy megadott háromszög oldalait, mint egy-egy kör átmérőjét. A hozzájuk tartozó három kör hatványpontja milyen összefüggésben van a háromszöggel?