Cím: 1947. Beszámoló a Bolyai János tanulóversenyről
Füzet: 1948/május, 111 - 114. oldal  PDF  |  MathML 
Témakör(ök): Kürschák József (korábban Eötvös Loránd)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Hírt adtunk a Bolyai János matematikai tanulóverseny lefolyásáról és nyerteseiről. Az alábbiakban ismertetjük a versenyre beérkezett dolgozatokat és olvasóink megoldásait.
A nyertes dolgozatokból átvett megoldásokat szószerint közöljük, a szerkesztő szövegkiegészítéseit [ ]-zárójelbe tesszük.

 

I. Mutassuk meg, hogy ha n páratlan szám, akkor
46n+296⋅13n
osztható 1947-tel!
 

I. Megoldás: [n=2k+1(k=0,1,2,...) alakban írható, mivel páratlan szám.]
462k+1+296⋅132k+1=46⋅462k+3848⋅132k==2(23⋅2116k+1924⋅169k)=2{23⋅2116k+(1947-23)⋅169k}==2{1947⋅169k+23(2116k-169k)}.2116-169=1947,tehát2116k-169k==[(2116-169)(2116k-1+2116k-2⋅169+...+2116⋅169k-2+169k-1)]=1947q


és
1947⋅169k+23(2116k-169k)=1947Q,
ahol q és Q egész szám.
 

Pollák György versenynyertes dolgozatából.

Megoldotta: Fülöp M., Tóth T. versenydolgozata, továbbá Kocsis K., Párkány M., Tamás H.
 

Megjegyzés: A megoldás lényegében a 462k+1+296⋅132k+1=46⋅462k+296⋅13⋅132k=46(462k-132k)+(46+296⋅13)⋅132k átalakítást használja.
 

II. Megoldás: 462k+1+296⋅132k+1={462k+1+(296⋅13)2k+1}-132k+1(2962k-1).
Az első tag osztható 46+296⋅13=2⋅1947-tel, 2962k-1 pedig (296+1)(296-1)=9⋅33⋅59⋅5=1947⋅45-tel, tehát az egész kifejezés osztható 1947-tel.
Kis hibával megoldotta Kántor K., Gaál E. versenydolgozata.
 

III. Megoldás: 1947=33⋅59. Mivel an-bn osztható a-b-vel és ha n páratlan szám, akkor an+bn is osztható a+b-vel, így 46n+296⋅13n=46n-13n+9⋅33⋅13n osztható 46-13=33-mal és ha n páratlan
46n+296⋅13n=46n+13n+5⋅59⋅13n osztható 46+13=59-cel.
Mivel 33 és 59 relatív prím számok, tehát kell, hogy szorzatuk: 33⋅59=1947 is osztója legyen 46n+206⋅13n-nek, ha n páratlan szám.
 

Vermes Róbert (Bp.-i Zsidó gimn. VIII. o.)
Megoldotta: Szőke L. versenydolgozata, továbbá Gaál I., Szépfalussy P.
 

IV. Megoldás: Állításunkat teljes indukcióval bizonyítjuk:
ha n=1,
46+296⋅13=2⋅1947.

Tegyük fel, hogy valamely n páratlan számra már tudjuk a tétel helyességét 46n+296⋅13n=1947⋅q, q egész. Innen 296⋅13n=1947⋅q-46n. Vizsgáljuk az összeget a következő páratlan kitevőre: 46n+2+296⋅13n+2=46n+2+(296⋅13n)132=46n+2+1947⋅q⋅132-13246n=1947⋅132q+46n(462-132)=1947⋅132q+46n33⋅59=1947⋅Q, ahol Q ismét egész szám. Ezzel bebizonyítottuk tételünket.
Megoldotta: Máyer I., Abonyi I., Síposs G. versenydolgozata, továbbá Gehér L., Gősy S., Károlyházy F.
Elég jó: Horváth M. versenydolgozata.
Osztásmaradékokkal számol (2 pont): Hosszú M., Izsák I., Korda J., Kővári T., Róna P., Sós Vera, Szabó Gy., Székely-Doby S., Ungár P. versenydolgozata, továbbá Gacsályi S.
Kis számolási hibával (2 pont): Czipszer J., Tarnóczi T.
 

II. Bizonyítsuk be, hogy hattagú társaságnak mindig van vagy három olyan tagja, akik kölcsönösen ismerik egymást, vagy három olyan, akik kölcsönösen nem ismerik egymást.
 

Sajnos, a ,,kölcsönös'' szó zavaró volt és néhányan egyoldalú ismeretségekre is gondoltak. Így persze nem igaz a tétel: állítsuk pl. libasorba a társaságot és mindenki ismerje az előtte levőket. Ekkor bármely két ember közt van ismeretség, de mindég csak egyoldalú. Erre a példára mutat rá Bede István versenydolgozatában. Többen azt is megjegyzik, hogy öttagú társaságra nem igaz a tétel. Erre meg ,,ellenpélda'' egy olyan öttagú társaság, amelyik körbe állítható úgy, hogy mindenki csak a két szomszédjával legyen ismeretségben.
 

Megoldás: Tekintsük a társaság egyik tagját, A urat. Ha ez kettőnél többet ismer és ezek közül kettő ismeri egymást, akkor már van három egymást kölcsönösen ismerő tag; ha pedig egyik sem ismeri a másikat, a második eset következik be. Ha A úr ismerőseinek száma nem haladja meg a kettőt, vagyis az előtte ismeretlenek száma legalább három, akkor ez utóbbiak vagy mind ismerik egymást, (1. eset) vagy van köztük legalább kettő, akik nem ismerik egymást. Minthogy ezek A úr előtt is ismeretlenek, a társaságnak megint van 3, kölcsönösen ismeretlen tagja.
 

Pollák György versenynyertes dolgozatából.

Megoldotta: Gaál I., Kővári T., Magyar Á. Sz., Sós Vera (lényegtelen hibával), Ungár P. versenydolgozata, továbbá Czipszer J., Károlyházy F., Róna P., Személyi J.
Elég jó (2 pont): Párkány M., Tarnóczi T. megoldása.
Van gondolat: Izsák I., Szőke L., Török A. versenydolgozatában.
 

III. Egy körlapot feleakkora átmérőjű körlapokkal akarunk befedni. Hogyan tehetjük ezt meg a legkevesebb számú körlappal?
 

Megoldás: [Az általánosság megszorítása nélkül feltehetjük, hogy] a befödendő kör sugara legyen 1.
1. [Hét kis körrel le lehet fedni a nagyot.] Beleírunk egy szabályos hatszöget, oldalainak középpontjai köré írunk egy-egy 1/2 sugarú kört, továbbá az eredeti kör középpontja köré is írunk egyet és azt állítjuk, hogy a kört lefedtük.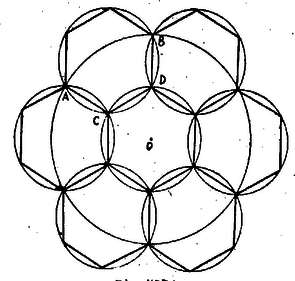
 
34. ÁBRA
 

[Tudjuk, hogy egybevágó szabályos hatszögekkel be lehet úgy fedni a síkot, hogy a hatszögek közt hézag sem marad, de egymást nem is fedik.] A 34. ábrán 7 darab [így illeszkedő] 1/2 oldalú szabályos hatszöget látunk. [Jelöljük a belső hatszög középpontját O-val; A és B legyen egy külső hatszögnek az a két szemközti csúcsa, melyek közül egyik sem csúcsa a belső hatszögnek, C és D pedig a belső hatszöggel közös csúcsok.] OA=1=OB, [mert OA és OB is szimmetriatengelye az ábrának s így kell, hogy C, ill. D is ezekre az egyenesekre essék. Már pedig OC=OD=CA=DB=1/2.] A berajzolt nagy kör sugara tehát 1, és az, mint látható, a hatszögek által befödetik. A hatszögek köré írt 1/2 sugarú körök ezért még inkább befedik a nagy kört.
2. Most azt bizonyítjuk, hogy hét körnél kevesebb nem elég. Az egy darab 1/2 sugarú kör által befedett körív végpontjainak távolsága ≤1, mert félsugarú körön belül bármely két pont távolsága ≤1. Ezért az egy kör által befedett ívhez tartozó középponti szög ≤60∘, vagyis az általunk megadotton kívül minden más lefedésnél [már] a körvonal lefedéséhez 7 kör kell, vagy több.
3. [Hét kis kör is csak az adott elrendezésben fedi be egészen a nagy kört.] Ha egy kör az O pontot fedi, akkor a kerületnek legfeljebb egy pontját fedi le, ha tehát a kerületet hét kör fedi le, akkor a középpont lefedéséhez feltétlenül kell egy nyolcadik. [Hat körrel pedig csak a megadott módon lehet lefedni az egész kerületet.]
 

Ungár Péter (VIII. o.) díjnyertes dolgozatából.


3 kivételével (3 pont): Fülöp M., Gaál E., Göndöcz I., Hosszú M.,
Megoldotta: Bede I. versenydolgozata, továbbá Czipszer J., Izsák I., Kővári T., Magyar Á. Sz., Máriaföldy Julianna, Máyer I., Pollák Gy., Sós Vera, Szabó Gy., Tavaszy M. és egy névtelen versenydolgozat, továbbá Gaál I.,. Gacsályi S., Gehér L., Gősy S., Károlyházy F., Madarassy Gy., Személyi J.
Elég jó (1 pont): Alkonyi I., Emőd (Eichner) I., Erdei M., Gargya L., Kántor K., Kertész I., Korda J., Lichtenstein Gy., Makay S., Róna P., Síposs G., Székely-Doby S., Szőke L., Varsányi F. versenydolgozata, továbbá Lichtenstein J., Párkány M., Serédi B., Szépfalussy P., Tarnóczi T., Vermes R. megoldása.
 

Megjegyzés: A probléma a következő módon általánosítható. Vegyünk kör helyett bármilyen konvex idomot. ‐ Konvexnek nevezünk egy idomot, ,,ha sehol sincs behorpadva'', vagyis ha bármely két a belsejében fekvő pontot összekötve az összekötő egyenes is a belsejében lesz. ‐ Kicsinyítsük le az idomot 2:1 arányban és ilyenekkel próbáljuk meg lefedni a nagyot, de úgy, hogy a kis idomokat közben el ne forgassuk, csak önmagukkal és a naggyal párhuzamos helyzetben tologassuk. Egy háromszög befedésére pl. 4 feleakkora háromszög elég, ha az oldalak középpontjait összekötjük, de ekkor a középső kis háromszög 180∘-kal el van fordítva. Párhuzamos háromszögekből már hatra van szükség. ‐ Hajós György vetette fel a kérdést, hogy általában hány párhuzamos, feleakkora idom szükséges a befedéshez. Ő is, Kárteszi Ferenc is, megtalálták a választ; bebizonyították, hogy hét kis idom, bármilyen konvex idomnál elegendő. Kevesebb nem lehet általában elegendő, de háromszögnél 6 kis idom is elegendő, paralelogrammánál már 4, trapéznál meg az alakjától függően 5 vagy 6.