| Cím: | Jelentés Az 1947. évi Első Országos Középiskolai Matematikaversenyről | ||
| Szerző(k): | Surányi János , Szőkefalvi-Nagy Béla | ||
| Füzet: | 1947/november, 11 - 20. oldal |  PDF | MathML PDF | MathML |
|
| Témakör(ök): | OKTV | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A szegedi matematikusok a középiskolai matematikai lapok elindításával együtt azt is elhatározták, hogy minden tanév végén országos versenyt is rendeznek. Az első versenyt 1947. évi június hó 14-én du. 3‐8-ig tartottuk egyidőben, azonos feltételek mellett Békéscsaba, Budapest, Csurgó, Debrecen, Nagykőrös, Nyíregyháza, Orosháza, Pannonhalma, Pécs, Szeged és Zalaegerszeg városokban. Kezdő és haladó csoport közt választhattak a résztvevők, de a VII‐VIII. oszt. tanulók csak az utóbbiban indulhattak. A kezdők versenyének tételei a következők voltak: 1. Melyek azok a számok, melyek maguk is, négyzetük is, két egyenlő jegyre végződnek? 2. Egy egész számokból álló számsorozat minden tagja, a harmadiktól kezdve, az előző két tag összege. Bizonyítsuk be, hogy bizonyos tagtól kezdve a sorozat tagjai mind egyforma előjelűek. 3. Az háromszög -hoz tartozó súlyvonalának egy pontját összekötve a és csúcsokkal, a kapott egyenesek a szemközti oldalakat , -ban metszik. Bizonyítsuk be, hogy . A haladó verseny résztvevői pedig az alábbi feladatokat kapták: 1. Hányféleképp írhatjuk fel az 1‐6 számokat a dobókocka 6 lapjára? 2. Van-e az változónak olyan negyedfokú, 5 tagból álló kifejezése, melynek négyzete is 5 tagú? Határozzuk meg ezeket! 3. Bizonyítsuk be, hogy a pozitív és számok számtani és mértani közepének különbsége és közé esik. A bíráló bizottság gondos mérlegelés után a következő eredményt állapította meg: A kezdők csoportjában: I. díjat nyert: Gehér László, a zalaegerszegi gimnázium VI. o. tanulója. II. díjat nyert: Korányi Ádám (Szegedi piarista gimn V. b. o.), Korda Péter (Budapesti Berzsenyi gimn. V. b. o.), Szépfalussy Péter (Szegedi piarista gimn. VI. b. o.) és Turczi Gyula (Csurgói református gimn. VI. o.). Dícséretben részesült: Gábor Imre (Pannonhalmi gimn. VI. o.) és Neszmélyi András (Pannonhalmi gimn. V. o.). A haladó csoportban I. díjat nyert: Magyar Á. Szilveszter (Budapesti ciszterci gimn. VIII. o.) és Ungár Péter (Budapesti evangélikus gimn. VII. o.). II. díjat nyert: Izsák Imre (Zalaegerszegi gimn. VIII. o.), Kajtár Márton (Pannonhalmi gimn. VII. o.) és Károlyházi Frigyes (Budapesti piarista gimn. VII. b. o.). III. díjat nyert: Gaál Egon (Budapesti ciszterci gimn. VIII. o.), Róna Péter (Budapesti evangélikus gimn. VI. o.) és Székely Dobi Sándor (Budapesti Szt. László gimn. VIII. o.). Dicséretben részesült: Bognár János (Budapesti evangélikus gimn. V. o.) és Hosszu Miklós (Csurgói református gimn. VIII. o.). A beérkezett dolgozatokról az alábbiakban számolunk be: Kezdő csoport: 1. feladat I. megoldása: Mivel , azért egy szám négyzetének utolsó két jegye a szám utolsó két jegyéből alkotott szám négyzetének utolsó két jegyével azonos. A két egyező jegyből álló számok négyzetei közül a -án kívül a -nek áll két egyező jegy a végén, tehát a -ra és -ra végződő számok tesznek eleget a feltételnek. Megoldotta: Simon E. II. megoldás: Az első megoldás szerint olyan számot keresünk, melyre utolsó két jegye egyenlő. Ez megegyezik utolsó két jegyével. Ennek a számnak utolsó jegye egyes jegyével egyezik meg, utolsó előtti jegye pedig annál egyeseinek és -eseinek összegével több. Tehát kell, hogy az utóbbi osztható legyen tízzel, ilyen számjegy és . Megoldotta: Sichermann Ilse, Vigh T. Részben oldotta meg: Berendik I., Dach Gy., Lengyel E., Mády Erzsébet. Van gondolat: Kenyeres M., Kovács A., Krausz T. megoldásában. 2. feladat megoldása: Elegendő azt bebizonyítani, hogy vagy van két egymásután következő tag, melyeknek előjele egyenlő, vagy előfordul a . Tekintve, hogy különböző előjelű számokat úgy vonunk össze, hogy a kisebbiket kivonjuk a nagyobbikból és a nagyobb előjelét írjuk eléje, míg az előjelek váltakoznak, minden tag abszolút értékre kisebb, mint az előtte levő abszolút értéke, , tehát a sorozat számainak abszolút értéke csökken. Bizonyos számú tag után a csökkenés lehetetlensége miatt (pozitív egész számok csökkenő sorozata csak véges számú tagból állhat) az abszolút értéknek növekednie kell, tehát a kérdéses tag abszolút értéke nagyobb lesz, mint az előtte lévőé. Az összevonás szabályai szerint a nagyobb tartja meg előjelét, tehát a kérdéses tag után következő tag előjele olyan lesz, mint az előzőé. Tehát két egymásután következő tag előjele egyenlő, a tétel be van bizonyítva. Gehér László. A megoldást pedzi: Brezsán F., Dach Gy., Kiss Z., Szittya O. Van gondolat: Kenyeres M., Krausz T., Simon E. dolgozatában. Megjegyzés: Ennek a tételnek az okára a következő mutat rá. Nevezzünk Fibonacci-féle sorozatnak minden olyan , , , , sorozatot, melyben a harmadik tagtól mindegyik az előző kettő összege: . Egy ilyen sorozatot nyilván az első két tagja egyértelműen meghatározza. Az is világos, hogy ha egy Fibonacci sorozat minden tagját megszorozzuk ugyanazzal a számmal, vagy ha két Fibonacci-féle sorozatot összeadunk, ismét Fibonacci-féle sorozatot kapunk. Hogy még egy kicsit ismerkedjünk velük, nézzük meg, nincs-e köztük mértani sor is. (Hogy számtani nincs a csupa -ból állón kívül, az könnyen látható). Az , , , sorozat Fibonacci-féle, ha Lényegében tehát két ilyen mértani sor van: ( és tetszőleges.) Az előbbi állandó, az utóbbi végig változó előjelű. De ha két Fibonacci-féle sorozatot ismerünk, melynek tagjai nem arányosak, akkor ezekkel már bármelyik előállítható. Esetünkben pl. ha , , , egy tetszőleges Fibonacci-féle sorozat, akkor csak az -t és -t kell úgy választani, hogy az Ekkor az: sorozat megjegyzéseink szerint Fibonacci-féle, amelynek első tagja , második tagja . Mivel pedig az első két tagja egyértelműen meghatározza a Fibonacci-féle sorozatot, tehát kell, hogy legyen. Kérdés most már, milyen előjelű ez a kifejezés? Az első tag előjele állandó (ugyanaz, mint -é), a másodiké váltakozó. Ha , akkor a már ismert váltakozó előjelű mértani sort kapjuk. Ha , akkor azt kell megnézni, hogy és közül melyik együtthatója nagyobb abszolút értékű. Mivel , így , . Ennek folytán hatványai minden határon túl nőnek, hatványai pedig minden határon túl csökkennek (13. és 28. feladat) és így elég nagy indextől kezdve minden tag előjele olyan, mint -é. Kivétel csak az a sor, amelyben az első és második tag hányadosa: , mivel azonban ez irracionális szám (33. feladat), így ez nem következhetik be, ha és egész. Sokan azt vizsgálták, hogy az egymásutáni tagok hogyan tevődnek össze az első és második tagból és abból próbálnak következtetni, hogy a második tag együtthatója mindig többel nő. Ez az út is járható, de ekkor nem az együtthatók különbsége, hanem hányadosa az irányadó, mert ha , akkor a törtek és az hányados viszonyát kell megvizsgálni. Megmutatható, hogy a törtek is értéket közelítik meg tetszőleges kis hibával, ha csak elég nagy, mégpedig váltakozva kisebbek és nagyobbak nála. Így a sorozat állandó előjelű valahonnan kezdve, ha csak nem , ami viszont egész számokból álló sorozatra nem következhetik be. Ezt a megoldást pedzi Neszmélyi András dolgozata. Kár, hogy állításait nem próbálja indokolni. 3. feladat. A oldal felező pontját jelöljük -sel. I. megoldás: Hosszabbítsuk meg az egyenest és -en túl mérjük rá az távolságot; így kapjuk a pontot (4. ábra). 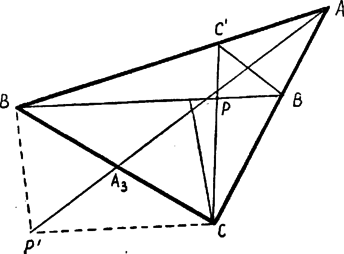 négyszög parallelogramma, mert átlói felezik egymást. Mivel a parallelogramma szemben fekvő oldalai párhuzamosak, és . A szárait párhuzamosok metszik, tehát a szárakon keletkező metszetek aránya egyenlő:
II. megoldás: Legyen és (5. ábra).  Ekkor Másfelől , tehát a szakaszt felezi s így és . Tehát a fenti aránypárból: Minthogy még (csúcsszögek), azért (két oldal aránya és a közbezárt szög egyenlő). Tehát és így .
III. megoldás: Tegyük fel, hogy . Ekkor van egy -n keresztülmenő egyenes, amely -vel párhuzamos és nem tartalmazza a pontot, hanem a és az egyenest két különböző helyen metszi: -t -ben, -t -ban, -t -ben (6. ábra). 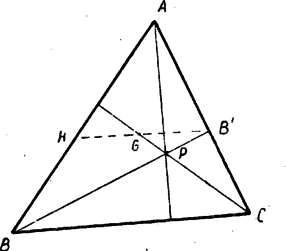 Másrészt alkalmazzuk ezt a tételt az pontból kiinduló sugarakra: Ellentmondásra jutottunk, tehát a és pont egybeesik.
IV. megoldás: Tudjuk, (35. feladat) hogy a trapéz átlóinak metszéspontja felezi a rajta keresztül az alappal párhuzamosan húzott egyenesnek a trapéz szárai közé eső szakaszát. Ebből is következik a tétel. Húzzunk ugyanis -n át párhuzamost -vel. Ez metssze -t a pontban. (7. ábra) és metszéspontja, az említett tétel folytán rajta kell, hogy feküdjék -en, s így azonos -vel, mert ez az és egyenes metszéspontja. Így átmegy -n, vagyis azonos -vel, tehát valóban . 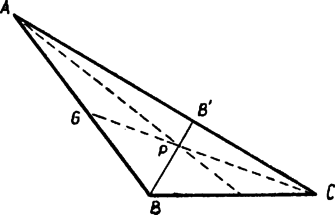 A használt tétel a következőképpen bizonyítható: Legyen az trapéz és átlóinak metszéspontja , az -n át -nel párhuzamosan húzott szakasz végpontjai , . Ekkor Megoldotta: Horváth G., Korda P., Neszmélyi A. Részben jó: Kovács Á. V. megoldás: Ha tetszésszerinti olyan pont, amely nem fekszik az , egyik oldal-egyenesén sem és ha , , a pontnak a háromszög , , illetőleg pontjából a szemközti oldalra való vetülete, akkor Ceva tétele szerint: (81. feladat. Megoldását lásd 33‐34. l.-on.) Ha , akkor és így , amiből:
Megjegyzés: Ha megnézzük, az a két rész, amire a súlyvonal vágja a háromszöget, nem igen hasonlít egymásra, mégis csak azon múlik mindegyik bizonyítás, hogy van valami rokonság a rajz jobb és balfele közt. Egész hasonlóan felel meg a két rész egymásnak, mintha tükörbe nézünk, mi és a tükörképünk. A megfelelő pontok előtte és mögötte egyenlő távol vannak, csak éppen az a furcsaság van a súlyvonal esetében, hogy a távolságot itt nem merőlegesen célszerű mérni, hanem ferdén: a oldal irányában. A tükrözés analógiájára ,,leképezés''-ről beszél a geometria, ha valamilyen módon két ábrát pontról-pontra megfeleltetünk egymásnak, akkor is, ha azoknak látszólag nem sok közük van egymáshoz. Az itt szereplő leképzést ,,affin tükrözés''-nek nevezik. Így jellemezhetjük általában: ha és a sík két nem párhuzamos egyenese (esetünkben az és a egyenes) és a sík egy tetszőleges pontja, akkor azt a pontot, amelyre a) , b) a szakaszt az egyenes felezi, a pont tengelyű és irányú affin tükörképének nevezzük. (Ha az tengelyen rajta van, akkor .) Ha , akkor az -tengelyű közönséges tükrözésről van szó. Ha torzít is ez a ,,tükrözés'', mégsem torzít el mindent és épp ez teszi használhatóvá. Tételünk nyilván következni fog abból, hogy az affin tükrözésnél egyenesnek a képe is egyenes. Legyen ugyanis egy tetszőleges egyenes a síkban, egy határozott és tetszésszerinti pontja, és az affin tükörképeik, és a és metszéspontja -szel. a) Ha az tengelyt a pontban metszi, akkor , tehát egyben , következésképpen rajta van a egyenesen. b) Ha párhuzamos -szel, akkor a négyszög parallelogramma, tehát , és így egyben ; következésképpen a négyszög két oldala párhuzamos és egyenlő, tehát szintén parallelogramma, azaz rajta van a -ből -szel párhuzamosan húzott egyenesen. Tekintsük már most azt az affin tükrözést, amelynek tengelye az súlyvonala, iránya pedig a egyenes. A és pont egymás tükörképei lévén, a és egyenesek egymás tükörképei. Általában, ha az egy tetszőleges pontja, akkor és egymás tükörképei. A és egyenesek metszéspontjának a tükörképe tehát a és egyenesek metszéspontjába kell, hogy essék. Tehát . Az -tengelyű és irányú affin tükrözés különös esete az általánosabb ,,-tengelyű és irányú'' általános affin leképezéseknek. Egy ilyen leképezésben a pont képe azáltal van meghatározva, hogy a) , b) adott arányban osztja a szakaszt. Egyenes képe ekkor is egyenes. Az affin tükrözést ezek közül az általánosabb affinitások közül kitünteti az a tulajdonsága, hogy bármely pont képének a képe egybeesik -vel. Haladó csoport: Az 1. feladatban az okoz nehézséget, hogy azok a számozások, amelyek a kocka elforgatásával azonos helyzetbe hozhatók, természetesen nem számíthatók különbözőnek. A versenyzők egy része azt számlálja meg, hány különböző helyzetbe lehet ugyanazt a dobókockát hozni, más részük közvetlenül a különböző dobókockákat számolja össze: I. megoldás: Egy a térben mereven rögzített kocka lapjaira féleképp írhatjuk fel a számokat. De mi azonosnak tekintjük mindazokat a felírásokat, melyek mozgatással fedésbe hozhatók. Ha tehát a kockát önmagával fedésbe hozó mozgatások száma (a helybenhagyás is egy mozgatás), akkor a kérdéses szám . Két egymás mellett fekvő és csúcs helyzete az elmozdítás után teljesen meghatározza a kocka helyzetét. Már most az csúcsot a rendelkezésre álló hely bármelyikébe átvihetjük. Ha helyét meghatározzuk, akkor még az -val szomszédos csúcs bármelyikébe juthat. Az összes lehetőség tehát és .
Megjegyzés: Ugyanígy pl. az ikozaéder lapjain az , , , számok féleképpen helyezhetők el. II. megoldás: Egy dobókocka különböző lehetséges helyzeteit megszámlálhatjuk így is: Az egyest mind a hat oldalra fordíthatjuk és mindegyik helyzetben ezen lap középpontja körül különböző helyzetbe forgatható a kocka, összesen tehát helyzetbe mozgatható el.
III. megoldás: Írjuk a kocka alsó lapjára pl. az -es számot. A többi számjegy -féleképpen helyezhető el. Ezek közül azonban 4‐4 eset azonos, csak helyzetileg különbözik egymástól. A megoldások száma tehát:
IV. megoldás: Ha pl. az -est mindig lefelé fordulva gondoljuk, akkor a fedőlapot tekintve eset lehetséges. Ragadjunk ki egy ilyent és vizsgáljuk a oldalsó szám szempontjából. Pl. jelölje és az alap és fedőlapot, akkor mondjuk a -mal szemben lehet a , az , vagy a , (ez eset) s mindegyik esetben a hátralévő két szám kétféleképpen helyezkedhetik el. Végeredményben tehát eset lehetséges.
Megoldották: Magyar Á. Szilveszter, Bognár János, Hosszú Miklós V. megoldás: Írjuk az -est az alsó lapra. A -est írhatjuk a szemközti lapra és valamelyik mellette lévő lapra (utóbbi esetben mellékes, melyikre.) A -ast első esetben lényegében csak egyféle helyzetben helyezhetjük el, míg utóbbi esetben mind a négy, még üres lap, lényegesen különböző esetre vezet. Mind az öt esetben a maradó szám az üres lapokra féleképpen írható. Megoldották: Dancziger E., Hosszú M., Kajtár M. és Kővári T. Elég jók: Szabó Á., Tamás I., Vincze P. A 2. feladatnál lényegében lehetséges esetet kell végigpróbálni, azonban kis ügyességgel a feladat kissé egyszerűsíthető és a szimmetriaviszonyok felhasználásával a próbálgatások száma csökkenthető. Megoldás: Ha egy keresett tulajdonságú polinom, akkor is. Elég tehát pl. , esetén) az alakú polinomokra szorítkozni. A két-két szélső tag nem tűnhet el, csak a -od fokútól a -ad fokúig terjedők. Ezek együtthatói: , , , , . Ha akár az első kettő, akár az utolsó kettő ezek közül eltűnik, mindig fennáll
Ha most az együtthatók közül négy eltűnik, akkor eltűnik valamelyik szélen mind a kettő, a másik szélről legalább az egyik, de akkor a másik is, mert teljesül (I) is, amiből könnyen következik állításunk, tekintve, hogy egyik együttható sem tűnhet el külön. Mindig teljesül tehát pl.: Így a keresett megoldások: , ; , . Mindegyik esetben , , tehát . Lényegében tehát megoldás van, valósak: Megoldotta: Magyar Á. Szilveszter Más megoldást adtak: Bakonyi Kornélia, Gaál E., Izsák I., Kajtár M., Károlyházi F., Kővári T., Lipták I., Loykó M., Róna P., Sós Vera, Szeleczky Sz. és Tamás I. Nem teljes megoldást adott: Ungár P., Bognár J., Hosszú M. Elég jók: Ember Gy., ifj. Huszka J., Szabó Á., Szűcs L., Boross R., Erdősi Gy., Madarász Z., Pál L., Tölgyesi L., Kovács G., Csák L. 3. feladat. I. megoldás: Feltehetjük, hogy pl. . Megoldották: Bakonyi Kornélia, Bognár J., Fülöp M., Gaál E., ifj. Gacsályi S., Hosszú M., Izsák I., Juhász E., Kajtár M., Károlyházi F., Lipták I., Lohonyai N., Szabó Á., Személyi J., Tamás I., Ungár P., Vörös M., Zility F. Elég jók: Reiner Éva, Sós Vera, Boda I., Herédi M., Szentmártony Z., Weninger O., Kovács G. II. megoldás: Bizonyítandó, hogy ha , Az elsőt fogjuk megmutatni, a második ugyanúgy bizonyítandó. -vel osztva és -et téve , átrendezve , ha , tehát monoton nő s így mindig fölött van.
(A jelentést Szőkefalvi Nagy Béla és Surányi János állította össze.) |