Cím: Ismerkedjünk a komplex számokkal 3.
Szerző(k):  Surányi János 
Füzet: 1948/szeptember, 131 - 144. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ismerkedjünk a komplex számokkal.1

(III. rész.)

 

Az első részben kitűzött feladatokat többen túl könnyünek tartották, mégis azok közül, akik komplex számokkal számolva oldották őket meg, többen eltévesztették. Épp azért kezdtük valóban könnyű kérdésekkel, hogy könnyen ellenőrizhessük magunkat, hogy helyes-e számolásunk. A legtöbben ehelyett jobbnak látták mindjárt az analitikus geometria nyelvére fordítani a kérdéseket.
 

1. Milyen hosszúak az 1-3i, 2i, -1-3i háromszög oldalai?
Megoldás: Jelöljük a komplex számokat A, B, C-vel. Az ABC▵ oldalai A-B=1-3i-2i=1-(2+3)i, B-C=2i+1+3i=1+(2+3)i, C-A=-1-3i-1+3i=-2, s így, mivel az oldalak hossza, továbbá valós és képzetes részük derékszögű háromszöget alkot, (A-B) hossza =(B-C) hossza = (-1)2+(2+3)2=8+43=22+3, (C-A) hossza pedig 2.
 

Gaál István (Szeged, ,,Dugonics András'' gimn. VII. o.)
 

Megoldotta: Findler M., Fried E., Gacsályi S., Gehér L., Gnóth M., Horváth Sz., Kővári T., Szépfalusy P., Szűcs L., Tarnóczi T., Vörös M.
 

2. Egy rombusz egyik oldala a z0+x0i vektor. Egyik átlója 45∘-os szöget zár be az X tengellyel. Írjuk fel a másik két csúcsát. Számítsuk ki őket, ha x0=3, y0=4.
Megoldás: (42. ábra.) Az X tengellyel 45∘-os szöget bezáró átló átmehet 0-n is, z0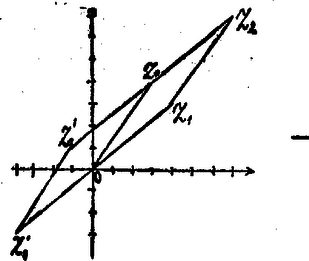-n is.
 
42. ábra
 

Utóbbi esetben a 0-án átmenő átló 135∘ szöget zár be a valós tengellyel. Az átló szimmetria-tengelye a rombusznak, de feladatunkban mindkét esetben a tengely-keresztnek is szimmetria-tengelye a 0-n átmenő átló. Első esetben az átlóra való tükrözésnél a valós és képzetes tengely pozitív fele cserélődik fel, a másodikban mindegyik tengely pozitív fele a másik negatív felével cserél helyet. Mindkét esetben z0 a vele átellenes z1 csúcsba megy át. Így első esetben z1=4+3i, általában z1=y0+x0i; másodikban z'1=-4-3i, általában z'1=-y0-x0i. A harmadik csúcs z2=z0+z1. Így a feltételnek a 0, x0+y0i, y0+x0i, (x0+y0)(1+i) és 0, x0+y0i, -y0-x0i, (x0-y0)(1-i) rombuszok, speciálisan a 0, 3+4i, 4+3i, 7+7i és a 0, 3+4i, -4-3i, -1+i rombuszok felelnek meg.
Megoldotta: Findler M., Gaál I., Gacsályi S., Gnóth M.
Csak az egyik rombuszt találta meg: Fried E., Gehér L., Horváth Sz., Kővári T., Szeghy I., Szépfalusy P., Szűcs L., Tarnóczi T., Vörös M.
 

3. Keressünk a 9⋅2-3⋅6i-hez olyan komplex számot, hogy összegük valós, különbségük képzetes legyen. Található-e ilyen bármely z=x+yi számhoz és melyik az? Geometriailag mi jellemzi ezt a számot?
 

Megoldás: Az adott számot z1-gyel, a keresettet z1-vel jelölve, a 0, z1, z1+z2, z2, parallelogramma átlói: z1+z2 és z1-z2, ha a feltétel teljesül, merőlegesek, tehát a négyszög rombusz és mivel ennek átlói a szögeket felezik, z2 csak z1-nek a valós tengelyre (a 0-n átmenő átlójára) vonatkozó tükörképe: z2=9⋅2+3⋅6i lehet és ez nyilvánvalóan meg is felel a feltételnek. Hasonlóan bármely z=x+yi számhoz van és pedig egyetlenegy ilyen szám a z=x-yi.
Gacsályi S., Gehér L., Szépfalusy P., Szűcs L. és Tarnóczi T. mutatta meg, azt is, hogy csak egyetlen ilyen szám van. Külön kapnak még 1-1 pontot.
Megoldotta még: Findler M., Fried E., Gnóth M., Horváth Sz., Kővári T., Paulik J.
Részben: Szeghy I., Vörös M.
 

4. A konjugált jelével írjuk fel egy komplex szám valós és képzetes részét. Jellemezzük a valós számokat.
Megoldás: Az előbbi feladat megoldásából látjuk, hogy ha z=x+yi, z+z¯=2x=2Re (z), z-z¯=Im (z)i, tehát
Re (z)=(z+z¯)2,Im (z)=z-z¯2i.(5)

A valós számokra Re (z)=z=z¯, Im (z)=0.
Megoldotta: Fried E., Gacsályi S., Gehér L., Gnóth M., Kővári T., Szűcs L., Tarnóczi T., Vörös M.
 

5. A z=x+yi komplex számhoz tartozó vektor hosszát a z komplex szám abszolút értékének nevezzük és |z|-vel jelöljük. Mutassuk meg, hogy ha z valós, akkor |z| a régi értelemben vett abszolút érték. Írjuk fel általában |z|-t x és y segítségével.
Megoldás: Már az 1. feladatban láttuk, hogy egy komplex számot ábrázoló vektor, továbbá valós és képzetes része derékszögű háromszöget alkot. Így |z|=x2+y2, ahol a négyzetgyök pozitív értéke értendő. Ha z valós, tehát y=0, akkor ez |x|-et adja.
Megoldotta: Findler M., Fried E., Gaál I., Gacsályi S., Gehér L., Gnóth M., Kővári T., Szépfalusy P., Sebes L., Tarnóczi T., Vörös M.
 

6. Az előbbi feladat jelöléseit használva, matassuk meg, hogy
|x|+|y|≥|z|≥|x|+|y|2.

Megoldás: Az egyenlőtlenség első fele a háromszög-egyenlőtlenség, alkalmazva az x, y, z oldalakból álló háromszögre. A második felében, miután pozitív számok szerepelnek, elég megmutatni, hogy a négyzetük közt fennáll az egyenlőtlenség:
x2+y2≥12(x2+y2+2|x||y|).Nullára redukálva, az
12(|x|-|y|)2≥0 helyes egyenlőtlenséghez jutunk, amiből következik, hogy az eredeti egyenlőtlenség is helyes. Az egyenlőtlenség első felében csak valós, vagy tiszta képzetes számoknál áll fenn egyenlőség, a második felében pedig csak ha |x|=|y|.
 

Kővári Tamás (Bp., Evangélikus gimn. VIII. o.)
 

Megoldotta: Findler M., Fried E., Gaál I, Gacsályi S., Gehér L., Szépfalusy P., Szűcs L., Tarnóczi T., Vörös M.
 

Megjegyzés: Az egyenlőtlenség második felét 2|z|≥|x|+|y| alakban írva, baloldalt az |z| átfogójú egyenlőszárú derékszögű háromszög befogóinak összege áll. Így azt mutattuk meg, hogy adott átfogó fölé írt derékszögű háromszögek közül az egyenlőszárúnak legnagyobb a kerülete. Keressetek erre a tételre elemi bizonyítást! (Lásd: 171. feladatot is.)
A II. rész ,,sürgős'' feladatai bizonyára több fejtőrést okoztak. Azt geometriailag legkönnyebb látni, hogy a műveletek alaptulajdonságai komplex számokra is érvényben maradnak.
Az összeadás kétféle sorrendje csak annyit jelent, hogy egy paralelogrammának egy csúcsából az átellenesbe a kerület egyik, vagy másik felén megyünk el. Az asszociatív tulajdonság pedig azt, hogy a három vektorból összerakott törtvonal-utat rövidítjük meg azzal, hogy az első két, ill. utolsó két szakasz helyett az egyik kezdőpontjától a másik végpontjához vezető utat járjuk meg.
A szorzásnál a Moivre formulákat használva, csak azt kell tudnunk, hogy külön az abszolút értékek szorzására, külön az irányszögek összeadása kommutatív, ill. asszociatív művelet. Ez pedig igaz, mert mindkét esetben valós számokról van már szó.
A disztributív tulajdonságnál: a(b+c)=ab+ac, ismét olvassuk le a két oldal geometriai értelmét, ha a, b, c komplex számok, b, c, b+c egy háromszöget alkotnak. Az ab, ac, a(b+c) vektorok ezekből úgy keletkeznek, hogy mindegyiket |a| arányban nyújtjuk és elforgatjuk a irányszögével mindegyiket. Ezek szerint nem csináltunk mást, mint az előbbi háromszöget nyújtottuk |a| arányban és a irányszögével elfordítottuk, tehát az utóbbi három vektor is háromszöget alkot és éppen ezt fejezi ki a vizsgált azonosság.
Most már vígan számolhatunk tovább komplex számokkal is, mint ahogy eddig számolni szoktunk, csak sohase felejtsük el, hogy i2=-1.
Szorozzunk össze két konjugált komplex számot. A szokásos jelöléseket használva, az ismert azonosság szerint
z⋅z¯=(x+yi)(x-yi)=x2-(yi)2=x2+y2=|z|2(6)

Ezzel egyszersmind találtunk egy módot, hogy komplex számok hányadosát közönséges komplex számmá alakítsuk. Legyen z1=x1+y1i, z2=x2+y2i, ,,i-tlenítsük'' a z1/z2 tört nevezőjét úgy, hogy a nevező konjugáltjával bővítjük a törtet:
z1z2=z1z2¯z2z2¯=(x1+y1i)(x2-y2i)x22+y22=x1x2+y1y2x22+y22+x2y1-x1y2x22+y22i.

Ismét többet mond azonban, ha a geometriai viszonyokat jobban feltüntető trigonometriai alakban írjuk fel a számokat: z1=r(cosφ+isinφ), z2=t(cosψ+isinψ). Ekkor olyan w=v(cosα+isinα) számot keresünk, melyet z2-vel szorozva, z1-et kapunk, tehát abszolút értékük szorzatából r-et, irányszögük összegéből pedig φ-t kapunk. Ennek egyetlen megoldása v=r/t, α=φ-ψ, vagyis
z1/z2=(r/t)[cos(φ-ψ)+isin(φ-ψ)](7)

Kezdetben még egy veszély ijesztett bennünket: vajon, ha az újfajta számokból akarunk négyzetgyököt vonni, arra nem kell-e majd még újabb számfajtát bevezetni? Van-e olyan komplex szám például, amelyre (x+yi)2=i?
A megoldandó egyenletet így írhatjuk: x2-y2+2xyi=i, ami csak úgy állhat, ha x2=y2 és 2xy=1. Itt x is, y is csak valós szám lehet. Ez esetben a második egyenletből következik, hogy x és y egyező előjelű, az elsőből pedig, ezt figyelembe véve, x=y kell, hogy legyen. Így a második egyenletből x2=1/2, tehát x=y=±1/2, tehát a keresett komplex szám 1+i2 és -1+i2 lehet és ez mind a kettő meg is felel a kívánt feltételnek.
Kevesebb írással is célhoz értünk volna, ha itt is a számok trigonometriai alakját használjuk és ebben az esetben nem is járt volna semmilyen hátránnyal. Általában azonban a számítás gyakorlati kivitelénél kényelmetlenebb trigonometriai táblákat használni, mint algebrai műveleteket végezni. Komplex szám négyzetgyökét pedig mindig ki lehet számítani úgy, hogy közben csak valós számokkal kell műveleteket végezni, még pedig alapműveleteken kívül csak négyzetgyökvonást, ha valamivel bonyolultabbak is lesznek a számítások a fentinél. Ennek keresztűlvitelét feladatul tűzzük ki.
A négyzetgyökvonás valóban nem vezet újabb nehézségekhez. Minden komplex számhoz találunk olyan komplex számot, ‐ egyébként kettőt, amelyek csak egy -1 szorzóban különböznek ‐ melynek a négyzete az adott komplex szám. Hogy egész nyugodtak lehessünk, nézzük meg, lehet-e magasabb gyököt is vonni komplex számokból anélkül, hogy tovább kellene bővítenünk számkörünket. Van-e pl. i-nek köbgyöke is a komplex számok közt? Válasszuk most a trigonometriai utat i=cos90∘+isin90∘. Köbgyöke (3) szerint (l. 98. o.) olyan komplex szám, melynek abszolút értékének harmadik hatványa 1, tehát |i3|=1, irányszögének háromszorosa pedig 90∘, vagyis
i3=cos30∘+isin30∘=3/2+i/2.

A számítás elvi része mindenesetre sokkal egyszerűbb, mint lett volna harmadfokú egyenletrendszer megoldása. Ezen az úton i négyzetgyökére azt kaptuk volna, hogy icos45∘+isin45∘=1/2+i/2. Igen ám, de hová sikkadt a másik megoldás? Írjuk át azt is trigonometriai alakra, -1/2-i/2=cos(180∘+45∘)+isin(180∘+45∘). Ennek négyzete valóban cos(360∘+90∘)+isin(360∘+90∘)=i mert a szöget 360∘-kal növelve, épp az eredeti irányba tértünk vissza. Innen ered hát a második megoldás. Két szög ugyanazt az irányt jelenti, ha azok 360∘-ban, vagy valamely egész többszörösében különböznek, de a felük már lényegesen különböző lehet.
Nézzük meg i3-re milyen más értéket kaphatunk hasonló módon?
(360∘+90∘)+isin(360∘+90∘)3==cos(120∘+30∘)+isin(120∘+30∘)=-3/2+i/2


és találunk egy harmadik megoldást is:
cos(720∘+90∘)+isin(720∘+90∘)3=cos270∘+isin270∘=-i.
Ha 3⋅360∘-kal növetjük az irányszöget, akkor már i3 első értékét kapjuk vissza és további 360∘-ok hozzáadásával is csak ezek az értékek ismétlődnek.
Így i3-re három különböző értéket kaptunk. Ezek irányszöge sorra 120∘-onkint növekszik, ami azt jelenti, hogy az elsőből a második és a harmadik megoldás ϱ1=cos120∘+isin120∘=-1/2+i3/2 és ϱ2=cos240∘+isin240∘=-1/2-i3/2-vel való szorzással adódik. Ezek maguk olyan számok, melyeknek harmadik hatványa 1. Épp ezen tulajdonságuk kapcsán találkoztunk már velük a 92. feladat megoldásában. Mint az 1 gyökeit, rövidebben harmadik egységgyököknek szokás nevezni őket.
Keressük meg most a hatodik egységgyököket, vagyis olyan komplex számokat, melyeknek hatodik hatványa 1. Az előbbi tapasztalatok után már előre ilyen alakba lesz jó az 1-et írni:
 


1=cos(k⋅360∘)+isin(k⋅360∘) és akkor 16 számára következő értékeket kapjuk: cos(k⋅60∘)+isin(k⋅60∘), ahol k tetszőleges egész szám. Elég azonban k-nak 0, 1, 2, 3, 4, 5 értékeket adni, hisz minden más (pozitív, vagy negatív) egész szám ezek valamelyikétől 6-nak, tehát a megfelelő szög 6⋅60∘=360∘-nak egy egész többszörösében különbözik. Így a hatodik egységgyökök
ε0=cos0∘+isin0∘=1,ε1=cos60∘+isin60∘=1/2+i3/2,ε2=cos120∘+isin120∘=-1/2+i3/2,ε3=cos180∘+isin180∘=-1,ε4=cos240∘+isin240∘=-1/2-i3/2ésε5=cos300∘+isin300∘=1/2-i3/2.



Ezek közt ott találjuk az előbbi harmadik egységgyököket is: ε2=ϱ1, ε4=ϱ2, -1-et meg ezzel a kifejezésmóddal második egységgyöknek nevezhetjük, 1 természetesen akárhanyadik kitevőnél mindig szerepel az egységgyökök közt. ε1 és ε5 azonban alacsonyabb kitevővel nem egységgyökök. A többi egységgyökök ε1-nek hatványai: εk=ε1k. De ugyanez a tulajdonsága megvan ε5-nek is, ennek a hatványai közt is előfordulnak az összes hatodik egységgyökök, csak épp fordított sorrendben, mert
ε5=cos(360∘-60∘)+isin(360∘-60∘),s ígyε5k=cos(k⋅360∘-k⋅60∘)+isin(k⋅360∘-k⋅60∘)==cos(360∘-k⋅60∘)+isin(360∘-k⋅60∘)==cos{(6-k)⋅60∘}+isin{(6-k)⋅60∘}=ε6-k.
Az ilyen egységgyököket, melyeknek hatványai sorra kiadják az összes ugyanannyiadik egységgyököt, primitív egységgyöknek nevezzük. Ehhez természetesen mindig meg kell mondani a gyökkitevőt is. ε2=ϱ1 pl. primitív harmadik egységgyök, mert ϱ12=ϱ2, ϱ13=1, (hasonlóan ϱ22=ϱ1), de nem primitív hatodik egységgyök, hisz hatványai csak három különböző értéket vetnek fel.
Az ε0, ε1, ε2, ε3, ε4, ε5 pontok 0-tól mind 1 távolságra vannak, vagyis a 0 körüli 1 sugárral rajzolt körön. Ezt a kört, miután sok szerepe van a komplex számok körében, röviden egységkör néven szokás emlegetni. Az egységkörön ezek az egységgyökök egymáshoz képest egyenlő 60∘-os szögekkel elforgatva helyezkednek el, vagyis egy szabályos hatszög csúcsait alkotják.
Most már az utolsó feltett kérdés sem okoz nehézséget. Legyen w=t(cosψ+isinψ) valamely komplex szám és n tetszőleges pozitív egész szám, keressük a zn=w egyenlet megoldásait, vagyis w n-edik gyökeit. Jelöljük t1n-nel t-nek a pozitív valós n-edik gyökét (amit eddig egy pozitív szám n-edik gyökén értettünk), akkor z=t1n[cos(ψ/n)+isin(ψ/n)], továbbá megfelelnek mindazok a számok, melyek irányszöge ettől 360∘/n-nek valamely egész többszörösében különbözik. Miután az irányszög növelése egy 1 abszolút értékű számmal való szorzással fejezhető ki, tehát megfelelnek a fenti szám εn(k)=cos(k⋅360∘/n)+isin(k⋅360∘/n)-szeresei is, (k=0, 1, 2, ..., n-1). Így
wn=t(cosψ+isinψ)n=t1n[cos(ψ/n+k⋅360∘/n)++isin(ψ/n+k⋅360∘/n)](k=0,1,2,...,n-1).(8)

εn(k) ‐ amit különben nyugodtan írhatnánk εnk hatványnak is, hisz εn(k)=εn(1)k ‐ az n-edik egységgyököket jelenti. Ha hozzájuk számítjuk az 1-et is, akkor ezek ismét egy az egységkörbe írt szabályos n-szög csúcsai. Ez a szabályos sokszög szimmetrikus a valós tengelyre, mert a szabályos sokszög egy csúcsán (+1) és középpontján (0) átmenő egyenes szimmetriatengely. Ez azt is jelenti, hogy a csúcsokat jellemző számok, tehát az egységgyökök összege valós szám 1+εn(1)+εn(2)+...+εn(n-1)=r valós. (pl. n=2, 3, 4, 6 esetben ez az összeg mindig 0-t ad). Próbáljuk meg kiszámítani r értékét az általános esetben. Azt kínálkozik itt felhasználni, hogy a többi csúcsokon át is húzhatók ilyen szimetriaegyenesek. Ha a sokszöget úgy forgatjuk el, hogy egy másik csúcs kerüljön a pozitív valós tengelyre, akkor újra valós, sőt ugyanaz lesz az ,,elforgatott'' összeg értéke is. Forgassuk a +1 helyébe, mondjuk az egyik vele szomszédos csúcsot. Ezt elérhetjük pl. εn(1)-gyel való szorzással:
εn(1)r=1+εn(1)+...+εn(n-1)=r.
Ha n>1, εn(1)≠1 s így r=0 kell legyen minden n-re.
Hogy az összeg εn(1)-gyel való szorzásnál önmagába megy át, az közvetlenül is látható, hisz minden tagból szorzás után az utána következő lesz, az utolsónak pedig az εn(1)-szerese +1, vagyis az első tag. Algebrailag azonban még gyorsabban is beláthatjuk ezt a tényt. Az egységgyökök a zn=1 egyenlet megoldásai. Válasszuk le ebből a z=1 gyököt, vagyis redukáljuk az egyenletet 0-ra és osszunk az 1-hez tartozó (z-1) gyöktényezővel (L. 126 ‐ 127 ‐ 128. feladat, 117 ‐ 121. old.) Kapjuk, hogy
1+z+z2+...+zn-1=0.
[ A balodali mértani sor összege valóban (zn-1)/(z-1).] A többi egységgyökök ennek az egyenletnek is eleget tesznek, többek közt eleget tesz εn(1) is. Mivel ennek magasabb hatványai a további egységgyökök, nyerjük ismét a fenti eredményt. Mivel az utóbbi egyenletnek ismerjük mind az n-1 gyökét (több az idézett feladatok értelmében nem is lehet), a baloldali összeget még egy egyszerű alakban is tudjuk írni: elsőfokú tényezők (gyöktényezők) szorzataként:
1+z+z2+...+zn-1=(z-εn(1))(z-εn(2))...(z-εn(n-1)),
amiből az előbbi összefüggés ismét következik, ha a szorzatot z hatványai szerint rendezzük és azután az elsőfokú tag együthatóit összehasonlítjuk. Ha meg z=0-t írunk, akkor azt nyerjük, hogy εn(1)εn(2)...εn(n-1)=(-1)n-1 ami geometriailag közvetlenül nyilván való. (Miért?) Könnyen találhatók még hasonló összefüggések egységgyökök közt, néhányat ki is tűzünk feladatul.
Láttuk az alapműveletek geometriai értelmét. További érdekes eredményeket kapunk, ha függvények geometriai jelentését vizsgáljuk, Nézzük először az elsőfokú függvényt: w=az+b (a és b adott komplex számok). Egy ilyen függvény a komplex számsík minden z pontjához hozzárendel egy másik pontot, w-t. Ábrázoljuk ezt a pontot is ugyanazon számsíkon. Ha a=1, akkor minden pontot eltoltunk a b vektorral. Zárjuk most ki az eltolást. Legyen tehát b=0. Ha a valós, akkor 0-ból, mint centrumból, kiinduló nyujtásról (vagy összehúzásról) van szó. Ha viszont a komplex, de |a|=1, (tehát a=cosφ+isinφ) akkor 0 körül φ szöggel való forgatást kapunk. Minden elsőfokú függvény ebből a három átatakításból tevődik össze. Ily módon az elsőfokú függvény például egy háromszöget egy újabb háromszögbe alakít át, mely az eredetihez mindig hasonló lesz, de általában hozzá képest még el is van tolva (ha b≠0) és elforgatva (ha a nem valós).
Hasonlóan minden más függvény is minden geometriai alakzatot átalakít valamilyen másikba, képet rajzol róla, mely azonban sokszor nem is hasonlít az eredetihez. Inkább karikatúrája annak: rá lehet azért belőle az eredetire ismerni, annak éppen egyes tulajdonságait külön kidomborítja. A geometriai átalakításokat szokás (latin szóval) transzformációnak, másképp leképezésnek, vagy ábrázolásnak nevezni.
Egy egyváltozós komplex függvény mindig egy transzformációt jelent. Vizsgáljunk most egy olyat, amelyik már torztükröt tart a geometriai alakzatok elé, a w=w(z)=1/z függvényt. Írjuk z-t és w-t trigonometriai alakba: z=r(cosφ+isinφ), w=ϱ(cosψ+isinψ). Ekkor ϱ=1r, ψ=-φ. Két olyan pont van, amelyik összeesik a képével: z=±1. A valós tengely is önmagába megy át, de ez már úgy, hogy az egyes pontjai azért helyet cserélnek, de csak egymásközt. Az egységkör belsejében levők képe kívül lesz és megfordítva. ‐ Általában a pontok páronkint felelnek meg egymásnak: ha P képe P', akkor P'-é viszont P, mert w[w(z)]=w(1/z)=1/(1/z)=z. ‐ De önmagukba mennek át más vonalak is, így azon pontok összessége, melyekre r=1, vagyis az egységkör is. Ha |z|=1, akkor 1/z=z¯, tehát az egységkört tükrözi a leképezés a valós tengelyre. Végül önmagába megy át a képzetes tengely is, de itt már kétszeres helycserével: a pozitív és negatív fél helyet cserél és mindegyiken, még az egységkörön belüli szakasz és a kívül lévő félegyenes is. A 0-nak magának nem jut kép és megfordítva, nem is képe egy pontnak sem. Egy 0-n átmenő egyenes pontjai, tehát melyekre φ állandó, a ‐ φ irányszöge, tehát a valós tengelyre tükörkép helyzetű, egyenesen feküsznek.
Egy P pont és P' képe közti kapcsolatot könnyebb a geometria nyelvén elmondani, ha segítségül vesszük P'-nek a valós tengelyre vonatkozó P1 tükörképét (43. ábra).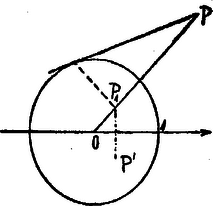
 
43. ábra
 

P és P1 ugyanazon a 0-n átmenő egyenesen fekszik és a 0-tól mért távolságaik szorzata 1. Egy ilyenfajta leképzés használatos a geometriában, körre vonatkozó tükrözés, vagy inverzió néven emlegetik. P-t és P1-et akkor nevezik egymás inverzeinek az O középpontú és r sugarú körre nézve, ha ugyanazon O-ból kiinduló félegyenesen feküsznek és OP⋅OP1=r2. Legyen P a körön kívül, akkor az inverz párját, P1-et úgy szerkeszthetjük meg (43. ábra), hogy egyrészt összekötjük P-t O-val, másrészt érintőt húzunk belőle a körhöz. Az érintési pont merőleges vetülete OP-re a P1 pont. P1 inverze viszont P.
A w=1/z leképzés minden P ponthoz az egységkörre vonatkozó inverzének a valós tengelyre vonatkozó tükörképét rendeli (egy 0 középpontú r sugarú körre vonatkozó hasonló leképezést a w=r2/z függvénnyel állíthatunk elő). Így ennek a függvénynek a vizsgálatából a körre vonatkozó inverziót is megismerjük. Az inverziónak legnevezetesebb tulajdonsága, hogy egyenest körbe visz át, ‐ kivéve a 0-n átmenő egyeneseket, melyek, mint az elmondottakból már tudjuk ‐ önmagukba mennek át. De körök képe is ismét kör, vagy egyenes. Ennek megmutatására jellemeznünk kell a köröket és egyeneseket. Legyen a komplex számsíkon a egy r sugarú kör középpontja, z a kör egy pontja, ekkor (z-a) a kör sugara, tehát (6) alapján, mivel különbség konjugáltja a a tagok konjugáltjainak különbségével egyenlő,
r2=|z-a|2=(z-a)(z-a¯)=(z-a)(z¯-a¯)=zz¯-a¯z-az¯+aa¯.

Hasonló egyenletet nyerhetünk az egyenesekre is a következő módon. (Hasonlóan, mint az analitikus geometriában a Hesse-féle normálegyenletet származtathatjuk.) Legyen a egy az egyenes irányára merőleges egységnyi hosszúságú vektor (44. ábra).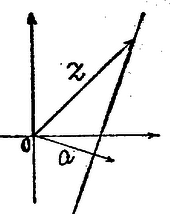
 
44. ábra
 

Az egyenes bármely z pontjához mutató vektornak az a-ra való vetülete (nagyság és irány szerint is) ugyanakkora. Ezt a vetületet úgy is megkaphatjuk, hogy elforgatjuk a z vektort a irányszögének negatívjával és aztán a valós tengelyre való vetületét vesszük, vagyis valós részét. Az elforgatást algebrailag a¯-val való szorzással fejezhetjük ki, így az egyenes egyenlete Re (a¯z)=d, ahol d valós szám (pozitív vagy negatív aszerint, hogy a 0-tól az egyenes felé, vagy ellenkező irányba mutat) jelentése a 0 pont távolsága az egyenestől. (Ha az egyenletben szereplő számokat valós és képzetes részre bontanánk, megkapnánk az analitikus geometriai normálegyenletet).
Itt csak az a lényeges, hogy a merőleges legyen az egyenesre, ha nem egységnyi hosszúságú, akkor d a 0-tól való távolság |a|-szorosát jelenti. (5) szerint és mivel könnyű látni (a bizonyítását feladatul adjuk), hogy szorzat konjugáltja a tényezők konjugáltjának szorzatával egyenlő (tehát a¯z¯=az¯), az egyenes egyenlete így írható: a¯z+az¯=2d. A körnek és egyenesnek az így nyert egyenlete könnyen egyesíthető, ha előbbit egy valós számmal végigszorozzuk. z és z¯ együtthatója most is, egymás konjugáltja lesz, a konstans tag pedig valós. Így 0-ra redukálva nyerjük a következő egyesített egyenletet:
αzz¯+β¯z+βz¯+γ=0,
ahol α és γ valós szám. Egyenes egyenletét kapjuk, ha α=0.
Most már nagyon könnyű látni, hogy a körök és egyenesek együttes serege önmagába megy át a w=1/z leképezésnél, vagyis a fenti egyenlet egy w-re vonatkozó hasonló szerkezetű egyenletbe transzformálódik. Ekkor ugyanis z=1/w és mivel könnyű látni, hogy 1/z¯=w, tehát z¯=1/w¯, ezeket az egyesített egyenletbe helyettesítve és megszorozva az egyenletet ww¯-tal nyerjük, hogy
γww¯+βw+β¯w¯+α=0.
Ez ismét kör vagy egyenes egyenlete. Ha egyenest képeztünk le, tehát α=0, akkor az új egyenletnek w=0 eleget tesz, tehát a kép egy 0-n átmenő kör, illetve ha γ=0, tehát az eredeti egyenes átment a 0-n, akkor a képe is 0-n átmenő egyenes. Akkor lesz viszont a kép egyenes, ha γ= volt, tehát a 0-n átmenő körök és egyenesek képei az egyenesek.
 

Megjegyezzük, hogy a 7. feladat kapcsán is végezhettük volna a bizonyítást (csak nem akartunk a feladat megoldásának elébe vágni). Ajánljuk olvasóinknak, hogy ha megoldották a feladatot, végezzék el annak segítségével a bizonyítást.
 

Az inverzió elmondott tulajdonsága segítségével sikerült egy Mohr nevű dán geométernek bebizonyítania, majd miután eredménye nem vált közismertté, egy évszázad mulva az olasz Mascheroninak (ejtsd Maszkeróni) újra rájönnie, hogy minden szerkesztés, ami körzövel és vonalzóval elvégezhető, elvégezhető, a vonalzót félretéve, csak körzővel is. Majd egyszer erről is elbeszélgetünk.
 

Egy másik érdekes összefüggésre vezet a w=(z+1/z) függvény. Írjuk z-t ismét trigonometrikus alakba: z=r(cosφ+isinφ) és vizsgáljuk milyen görbékbe mennek át a 0-n átmenő egyenesek és a 0 körüli koncentrikus körök. Utóbbiakat r= állandó, előbbieket φ= állandó jellemzi. Válasszuk szét w-t valós és képzetes részre: w=u+iv,  u=(r+1/r)cosφ  v=(r-1/r)sinφ. Ha r állandó és r≠1, akkor a két egyenletből φ-t kiküszöbölve u2(r+1/r)2+v2(r-1/r)2=1 ellipszisek egyenletét kapjuk. Tengelyeik élhossza r+1/r és |r-1/r|. Fókuszaik távolságát kiszámítva: c2=(r+1/r)2-(r-1/r)2=4, vagyis azt nyerjük, hogy az összes ellipszisek fókuszai közösek: a -2, 2 pontok.
Ha r=1, akkor v=0, u=2cosφ, tehát az egységkörön futó pont képe a (-2,2) szakaszt járja be, de oda-vissza, míg φ 0-tól 360∘-ig változik.
Legyen most φ állandó, ekkor r-et kell kiküszöbölni, ami ha φ≠0, 90∘, 180∘, 270∘, az előbbi számítás alapján úgy történhetik, hogy cosφ-vel, ill. sinφ-vel osztunk és a hányadosok négyzeteinek különbségét vesszük:
u2cos2φ-v2sin2φ=4
ezek tehát hiperbolák 2|cosφ| és 2|sinφ| féltengelyekkel. Számítsuk ki ismét a fókuszok fél távolságát, c-t:
c2=4cos2φ+4sin2φ=4,
a fókuszok tehát ismét a -2, +2 pontok. Ha φ=0, akkor v=0, u=r+1/r=(r2+1)/r=(r-1)2/r+2≥2. Ha φ=180∘, akkor v=0, u=-(r+1/r)≤-2, tehát a valós tengely képe saját maga lesz, de a (-2,2) szakasz kivételével és ismét kétszeresen (az r és 1/r pontok képe ugyanaz az u pont). Ha π=90∘, 270∘, u=0, v=±(r-1/r). A képzetes tengely pozitív és negatív felének külön-külön az egész képzetes tengely felel meg. Ezek a tengelyképek egy-egy elfajult hiperbolának tekinthetők.
 

Az ugyanazon két fókuszhoz tartozó összes ellipsziseket és hiperbolákat együtt konfokális kúpszeleteknek nevezzük. Egy ilyen ellipszis és egy hiperbola valamelyik metszéspontját véve, ahhoz húzott rádiusz vektorok közösek. Tudjuk azonban (105. és 106. feladat, 76‐77. o.), hogy az ellipszis érintője a rádiusz vektorok külső szögfelezője, a hiperboláé pedig a belső szögfelező. Ezek tehát (45. ábra) egymásra merőleges egyenesek.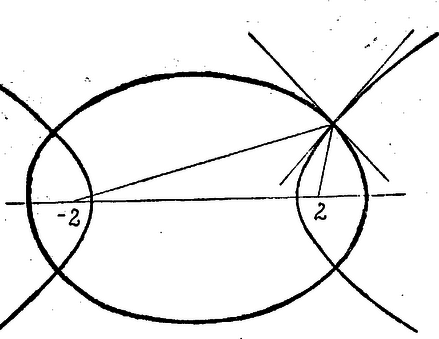
 
45. ábra
 

Ha két görbe metszi egymást, a metszéspontjukban húzott érintők szögét szokás röviden a két görbe hajlásszögének nevezni.
 

A konfokális kúpszeletek összes ellipszisei az összes hiperbolákat merőlegesen metszik át. Merőlegesen metszették egymást a 0-középpontú körök és a 0-n átmenő egyenesek is, amiknek a konfokális kúpszeletek a képei. Ez nem vétetlen, mert a komplex változás függvények egy nevezetes csoportjának megvan az a tulajdonsága, hogy úgy képezi le a síkot, hogy a leképzésnél a szögek irány és nagyság szerint ugyanakkorák maradnak, legfeljebb egyes pontokban bomolhat meg ez a szabályosság, mint föntebb a -2 és 2 pontokban. (Ez a tulajdonsága van azoknak a függvényeknek, amelyek differenciálhatók a komplex változó szerint. Ez sokkal nagyobb megszorítás, mint egy valós változós függvénynél, hogy differenciálható legyen. pl. z¯, vagy |z| ami valósban a 0 pont kivételével differenciálható, már nem differenciálható, sehol sem. Kivételesek ebben az esetben is azok a pontok, ahol a függvény differenciálhányadosa nulla.) Az ilyen leképezések, a konform ábrázolások tana egy igen érdekes és változatos ága a komplex változós függvények tanának.
 

Befejzőül ismét egy könnyebb, elemi geometriai kérdést tárgyalunk meg: az 1941. évi XLV. b. Eötvös Lóránd matematikai tanulmányverseny III. tétele így szólt: ,,Egy körbeírt ABCDEF hatszög AB, CD és EF oldalai egyenlők a kör sugarával. Bebizonyítandó, hogy a többi három oldal felezőpontjai szabályos háromszöget határoznak meg.''
 

Ennek a tételnek igen elegáns (természetesen nem a legegyszerűbb) bizonyítását nyerjük komplex számok segítségével. Válasszuk a kör középpontját a komplex számsík 0 pontjának, sugarát mértékegységnek.
 

Ekkor az A pont valamilyen 1 abszolút értékű α komplex számot ábrázol. A B ponthoz úgy jutunk, hogy 60∘-kal továbbfordítjuk A-t az egységkörön. Ez algebrailag az ε=cos60∘+isin60∘ számmal való szorzást jelenti. A B pontot tehát a β=εα szám képviseli, C-t valamely γ szám, D-t δ=εγ, E-t η, F-et ζ=εη. A BC oldalfelező pontja ekkor (εα+γ)/2, hasonlóan DE és FA felezőpontja (εγ+η)/2 és (εη+α)/2. A kérdéses háromszög oldalait irány és nagyság szerint az a=(εγ+η-εα-γ)/2, b=(εη+α-εγ-η)/2, c=(εα+γ-εη-α)/2 vektorok (46. ábra).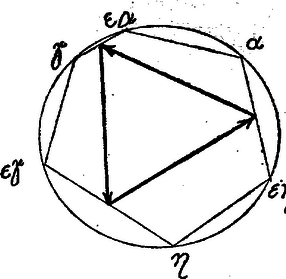
 
46. ábra
 

Azt kell megmutatnunk, ‐ mivel az oldalak irányítása a háromszög egy irányban való körbenjárásának felel meg, ‐ hogy valamely oldalát kezdőpontja körül 120∘-kal elforgatva a következő oldallal irány és nagyság szerint egyenlő vektort kapunk. A 120∘-os elforgatásnak ε2-tel való szorzás felel meg.
ε2a=ε2(εγ+η-εα-γ)/2=(ε2η-ε3α+(ε3-ε2)γ)/2.

Meg kell tehát vizsgálnunk még az ε hatványai közt lévő kapcsolatokat. ε3 irányszöge 180∘ és mivel abszolút értéke 1, ε3=-1, azaz ε3+1=(ε+1)(ε3-ε+1)=0. Mivel ε≠-1, kell, hogy ε2-ε+1=0 legyen. Innen ε2=ε-1, vagy ε-nal szorozva és átrendezve ε3-ε2=-ε. Ezeket felhasználva,
ε2a=[(ε-1)η+α-εγ]/2=b.

A háromszög tehát egyenlő szárú és a két szár közti szög 60∘ (a külső szöge 120∘), így kell, hogy egyenlő oldalú legyen.
Ismét ajánljuk, hogy keressétek a feladat elemi geometriai megoldását.
 

9. Bizonyítsuk be, hogy két komplex szám összegének, különbségének, szorzatának, ill. hányadosának konjugáltja egyenlő a két szám konjugáltjának összegével, különbségével, szorzatával, illetve hányadosával.
 

10. Számítsuk ki a 1/3-i4/3 komplex szám valós és képzetes részét algebrai úton (trigonometria felhasználása nélkül).
Elvégezhelő-e a négyzetgyökvonás bármely komplex számból algebrai úton, hogyan?
 

11. Bizonyítsuk be, hogy ha egy valós együtthatós algebrai egyenletnek egy komplex szám gyöke, akkor gyöke a konjugáltja is.
 

12. Számítsuk ki az n-edik egységgyökök négyzeteinek, köbeinek, ...n-1-edik hatványainak az összegét.
 

13. Jelöljük az 1-től különböző n-edik egységgyököket εn(1), εn(2), ...εn(n-1),-gyel. Számítsuk ki az
(εn(1)-1)(εn(2)-1)...(εn(n-1)-1)
szorzata értékét (a +1 csúcsból húzható átlók és oldalak szorzatát).
 

14. Hány 24-edik primitív egységgyök van? Jellemezzük geometriailag a 24-edik egységgyökök ábrázolásakor keletkező szabályos 24-szög azon csúcsait, melyek primitív egységgyököt ábrázolnak.
 

15. Legyen n adott egész szám és legyen ε egy primitív n-edik egységgyök, (tehát melynek n-edik hatványa 1 és melynek hatványai közt az összes n-edik egységgyök előfordul). Jellemezzük azokat a k hatványkitevőket, amik mellett εk szintén primitív n-edik egységgyök.
Vizsgáljuk meg a w=iz-iz+i leképezést a következő szempontokból:
 

16. Mi lesz ebben a leképezésben a valós tengely képe?
Van-e valami egyszerű kapcsolat két olyan pont képe közt, melyek az egységkörre vonatkozó inverziónál egymásba mennek át?
 

17. Mi lesz az egységkör képe, mi a vele koncentrikus köröké?
Hol feküsznek azon pontok képei, melyek a valós tengely fölötti félsíkban vannak. (Melyekre Im (z)>0)?
1Előző közleményünk megjelenése után értesültünk, hogy a komplex számok szorzásának ott követett bevezetési módját Rieger Richard már 23 éve alkalmazza középiskolai tanításában. Tőle származik a meggondolás eredményének következő megfogalmazása: a z=-2+i vektorból ép olyan lépésekkel jutunk a (-2+i)(3+2i) szorzatvektorhoz, mint amilyenekkel a z=1 vektorból a w=3+2i szorzó vektort megkapjuk.
Szele Tibor Riegertől függetlenül talált rá a szorzás ezen bevezetési módjára.