| Cím: | Ismerkedjünk a komplex számokkal 2. | ||
| Szerző(k): | Surányi János | ||
| Füzet: | 1948/május, 94 - 101. oldal |  PDF | MathML PDF | MathML |
|
| Témakör(ök): | Szakmai cikkek | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Bizonyára mind tudtok már ábrázolni bármilyen komplex számot a számsíkon s arra is rájöttetek, hogy a -től -höz mutató vektor (az a vektor, melyet -hez hozzáadva, -be jutunk); hogy a téglalap többi csúcsa: , , ; és hogy a hatszögé meg , , , , . A többi kérdésre még nem árulom el a választ, hátha van még, aki töri a fejét, az hadd gondolkodhasson tovább. Most már el is tudjuk valahogy képzelni a komplex számokat, össze is tudjuk adni őket, de szorozni még nem mindig. Ha tiszta képzetes számot szorzunk valóssal, pl. kell, hogy legyen az algebra szerint, de két képzetes számot is össze tudunk szorozni, ha továbbra is úgy számolunk, mint az algebrában eddig: , mert . Speciálisan ki tudjuk számítani további hatványait. Tudjuk, hogy -nek az a jellemző tulajdonsága, hogy . Ennélfogva , , , , és mondjuk pl. kell, hogy legyen. Hát ez elég furcsán hangzik. Mit lehet kiolvasni belőle? Összhangban van-e azzal, amiket előtte mondtunk a szorzásról? Két valós szám szorzatáról szól (2) is, ha és tényleg ekkor -t kapunk. Ha az egyik valós, a másik képzetes: , , vagy , ; végül, ha , két képzetes szám szorzatára -t ad (2). Idáig tehát minden rendben van, mégis jó lenne tudni, mit jelent ez a titokzatos formula. Első ránézésre ezt is nehéznek látszik kiolvasni belőle, de ha egy kicsit óvatosan indulunk neki, megkapjuk rá a választ. Az itt következő gondolatmenet Szele Tibor munkatársunktól származik. A szorzást úgy végeztük komplex számokkal, mint kéttagú algebrai kifejezések ,,beszorzását'' szoktuk, minden tagot mindegyikkel megszoroztuk. Először tehát most is azt vizsgáljuk meg, valós és képzetes számok közt mit jelent geometriailag a szorzás. A valós egység, az 1, arról nevezetes, hogy a számok közt ő az, aki ,,se nem oszt, se nem szoroz'', semmilyen szám nem változik meg, ha vele megszorozzuk. Egy valós szám -szerese már azt jelenti, hogy a számot változatlan nagyságban, de -tól épp ellentétes irányban kell felrajzolni. Más valós számmal, pl. 5-tel, szorozni egy valós számot, annyit jelent, hogy az őt ábrázoló távolságot ötszörösére megnyújtjuk. Ha a szorzó 1-nél kisebb, pl. , akkor, már kisebb távolsághoz jutunk, tehát helyesebb volna, ilyenkor összehúzásról beszélnünk, de az egyöntetűség kedvéért ezt is ,,-szorosára nyújtás''-nak fogjuk nevezni. Negatív számmal, pl. -vel való szorzatot is a távolság kétszerese ábrázolja, de ismét -tól a szorzandóval ellentétes irányban, (vagyis a szorzandó kétszeresének a -szerese). Hasonló a helyzet a képzetes tengelyen is: pozitív valós számmal való szorzás ismét egy, a szorzó arányában való nyújtást jelent, a -szerest a szorzandóval egyenlő távolság ábrázolja, de ellentétes oldalán, más negatív szorzónál pedig ismét a kettőt együtt kell csinálni: a szorzandót megnyújtva, az ellentétes oldalán kell ábrázolni. 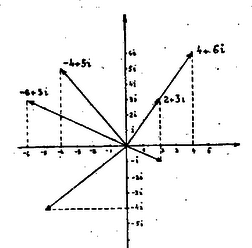 35. ábra Ha egy komplex számot szorzunk meg egy valós számmal, pl. , vagy (35. ábra), akkor a valós rész, a képzetes rész és a komplex számot ábrázoló vektor által bezárt derékszögű háromszög helyébe kapunk egy másikat, melynek befogói az eredetinek első esetben kétszerese, másodikban háromszorosa és -ból, illetve a valós tengelyről kiindulva, pozitív szorzó esetén az eredetiekkel egyező, negatív szorzónál velük ellentétes irányban párhuzamosak. Így valós számmal való szorzás geometriailag a komplex szám megnyújtását jelenti a szorzó abszolút értéke arányában, de negatív szorzó esetén az eredeti vektorral ellentétes irányban. Képzetes számmal szorozva, már a szorzat mindig más irányú, mint a szorzandó. Pl. 1 valós -szerese már a rá merőleges képzetes tengelyen fekszik. meg még -kal továbbfordulást jelent az óramutató járásával ellentétes irányban, ha a tengelyeket a szokott módon rajzoljuk. ‐ Ezt a forgásirányt röviden pozitív iránynak fogjuk nevezni tovább. és még 90‐90 fokkal továbbfordulást jelent. Ábrázoljuk most pl. -t (35. ábra). Rajzoljuk fel ismét a valós rész végpontjából a képzetes részt is. A keletkezett háromszöget pozitív irányában derékszöggel elfordítva, a mondottak szerint a valós és képzetes tengelyekkel párhuzamos befogói épp a szorzat valós, ill. képzetes részét ábrázolják. Így bármely vektor -szeresét az ugyanakkora, de pozitív irányban derékszöggel elforgatott vektor ábrázolja. Szorozzunk most már össze két komplex számot, pl. -t és -t. Ezt végezhetjük úgy, hogy -t szorozzuk meg 3-mal és -vel és a két kapott vektort összeadjuk. A szorzást ugyan (2)-vel értelmeztük és nem így, tehát 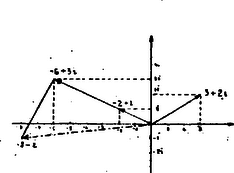 36. ábra A fenti szorzatot ebből a két vektorból téve össze (36. ábra), az egyik a irányába mutat, csak háromszor olyan hosszú; a másik vektor erre merőleges, mivel képzetes számmal szoroztunk, még pedig pozitív irányban és kétszer olyan hosszú, mint a vektor, ezt jelenti a szorzó. Így kaptunk egy derékszögű háromszöget: mintha csak a komplex számot ábrázoltuk volna, de úgy, hogy előbb a valós tengelyt a vektor irányába fordítottuk volna és új mértékegységet is választottunk volna: a vektor hosszát. Ezek szerint a szorzat-vektor iránya akkora szöggel van elfordítva a vektorhoz képest pozitív forgási irányban, mint amekkora szöget a vektor zár be a valós tengely pozitív felével; a hossza (abszolút értéke) pedig a szorzandó hosszaszor akkora, mint a szorzóé. Valóban Nevezzük általában azt a szöget, amelyet egy vektor a valós tengely pozitív felével bezár, a vektor irányszögének, jelölése . (Pl. , , , stb.) Ekkor a szorzat-vektor irányszöge a tényezők irányszögének összege; abszolút értéke pedig a két tényező abszolút értékének (a két vektor hosszának) szorzata. Az összeadás geometriai jelentését aránylag könnyű volt leolvasni, ha a számot valós és képzetes részével jellemeztük. A szorzat jellemzésére az irányszög és az abszolút érték bizonyult alkalmasnak. Ez is két olyan adat, mely egyértelműen meghatározza a vektort. Próbáljuk meg ezekkel kifejezni a komplex számot. Legyen egy komplex szám , abszolút értéke , irányszöge (37. ábra). Ekkor , és könnyű látni, hogy ez minden -re igaz, nemcsak hegyes szögekre. 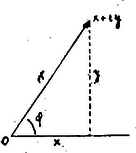 37. ábra Így . Most már a szorzás fenti geometriai értelmét is újra vissza tudjuk fordítani az algebra nyelvére. Legyen Itt a baloldalon kijelölt szorzást másképp is el tudjuk végezni: (2) szerint Így a trigonometriai függvények két jól ismert összefüggésének egy újabb levezetését is kaptuk mellékeredményül. 1 Speciálisan, ha , akkor nyerjük (2)-ből:
A (2) és (3) összefüggéseket Moivre-féle formuláknak nevezzük. Eddig nem esett szó az inverz műveletekről. A kivonáshoz nem is kell sok. Akár (2)-ből, de abból is, hogy egy szám negatívja az a szám, amelyet hozzáadva, 0-t kapunk, következik, hogy s így két komplex szám különbsége:
Nehezebb valamivel az osztás kérdése, de arra is megtalálhatjátok a választ. Ha így fogalmazzuk a feladatot: keressünk olyan komplex számot, amellyel egy adott komplex számot (pl. -t) megszorozva, egy másik adott komplex számot kapunk (pl. -t), akkor a szorzás geometriai jelentéséből könnyű megtalálni a választ. De az algebra is útbaigazít, csak az algebra nyelvén kell megfogalmazni a feladatot. Az osztást az algebrában törtekkel jelölhetjük ki: és akkor a kérdés az, át lehet-e ezt a törtet alakítani közönséges komplex számmá. Hasonló feladat, mint a gyöktelenítés, ha egy tört nevezőjében négyzetgyökös kifejezés is szerepelt. Olyan komplex számmal kellene ezt a törtet bővíteni, hogy a nevezőből valós szám legyen a bővítés után, tehát, hogy az első hatványát tartalmazó tag összevonás után ne maradjon. Ilyen van sok is. Egyet különösen könnyű megtalálni. Keressétek meg! Ha megtaláltátok, akkor meg is tanultatok számolni komplex számokkal és itt lesz az alkalom, hogy megpróbáljuk új tudományunkat a geometriában is értékesíteni. Egy kérdést azonban még tisztázni kell. Többször mondtuk azt, hogy valami igaz, ha az új számokkal is úgy lehet számolni, mint az algebrában szokás. Az új műveleteket minden esetre úgy értelmeztük, hogy azt mondtuk, számoljunk továbbra is úgy, mint az algebrában. Pl. szorozzunk két komplex számot úgy, ahogy kéttagú kifejezést kéttagúval szoktunk (de ne felejtsük el azután, hogy ). De az már nem biztos, hogy igaz ez akkor is, ha a kéttagúak tagjai nem vagy valós, vagy tiszta képzetes számok, hanem mindegyikük egy-egy tetszőleges komplex szám. Ez viszont kétségbeejtő, mert hiszen az algebrában annyi mindent csináltunk, hogy azt mind végigpróbálni, hogy igaz-e komplex számokra is, az kivihetetlen. Ilyenkor egy reményünk marad: hátha csak sok, de nem lényegesen másmilyen dolog az, amit csináltunk. A szorzás geometriai jelentését keresve, a kéttagú szorzását kéttagúval két lépésben végeztük el, ami az algebrában mindig megtehető, ilyenformán: Itt tehát csak azt kellett tudnunk, hogy kéttagú összeggel hogy szorzunk meg egy számot (tudniillik a összeadás eredményét), azután, hogy hogy szorzunk egy számmal kéttagú összeget (ezt kétszer is alkalmaztuk). Még ezek közül is elég az egyiket tudni, ha a másik helyett csak annyit tudunk, hogy a szorzat tényezői felcserélhetők. Azt is bizonyára legtöbben tudjátok, hogy többtagúak szorzását mindig szét lehet bontani kéttagúak szorzására. Pl. , stb. Nagyon sok számolást megpróbálhatnánk még szétboncolni ilyen egyszerűbb lépésekre, mindig azt találnánk, hogy visszavezethető az összeadás és szorzás következő öt tulajdonságára: (kommutatív műveletek), (asszociatív műveletek), végül (a szorzás az összeadással szemben disztributív művelet). Ajánlom, próbáljatok meg néhány algebrai számítást szételemezni ezekre a lépésekre. Lehet, nem mindre fogtok rátalálni, különösen az asszociatív törvényekre nem, de ne felejtsétek el, hogy többtagú összeget, ill. többtényezős szorzatot azért írhatunk zárójelek nélkül, mert úgyis mindegy a végeredmény szempontjából, melyik két tagnál, ill. tényezőnél kezdem a szorzást és hogy folytatom. (Persze, csak a végeredmény szempontjából mindegy, a részletösszegek és a részletszorzatok egészen mások lesznek.) Így több tagot, ill. több tényezőt zárójelek nélkül írni, az már az asszociatív törvény alkalmazása. Hogy ez nem magától értetődő, arra rávilágít a hatványozás példája. Ez már nem asszociatív művelet, pl. még nem is nagy szám, de már ; vagy egy 76 jegyű szám, két sorban még le lehet írni, , számjegyeivel viszont már egy 740 kötetes könyvtár is megtelnék 2. Így a feladat már egyáltalán nem ijesztő, magatok is utánaszámolhattok, hogy ez az öt tulajdonság igaz marad akkor is, ha , , komplex számokat jelentenek és a műveleteket köztük úgy végezzük, ahogy azokban megállapodtunk. Lássatok hát ismét munkához. Gyors válaszotokat várom a következőkre: Mi lesz két konjugált komplex szám szorzata? Mi a geometriai jelentése? Keressünk olyan komplex számot, mely két komplex szám hányadosával egyenlő. Mi az osztás geometriai jelentése? Hogy nyerhetjük a hányadost algebrai úton? Keressünk olyan komplex számot, melynek a négyzete . Hány ilyen szám van? Mely számok köbe ? Hát ilyen hány van? Melyek azok a számok, melyeknek hatodik hatványa 1? Hogy helyezkednek el ezek a számsíkban? Ha tetszőleges egész szám és egy tetszőleges komplex szám, keressünk olyan számot, melyre . Hány különböző ilyen számot találhatunk? A további kérdések már nem ilyen sürgősek, így azok már beleszámítanak a pontversenybe is. 7. Legyen , , a komplex számsík három pontja. Hol feküsznek azok a pontok, amelyekre: 8. Kiszámíthatjuk-e egy tetszőleges komplex szám négyzetgyökét úgy, hogy közben csak valós számokkal végzünk alapműveleteket, vagy gyökvonásokat? Ha igen, hogyan? 1Figyeljük meg azt is, hogy a szokásos meggondolások csak hegyes szögekre adják az eredményt és külön vizsgálják az érvényességét az egyes szögnegyedekben. Itt értelmezhetjük minden negyedre mindjárt a cosinus és sinus függvényeket úgy, hogy egy komplex szám valós, ill. képzetes része osztva az abszolút értékével. S ekkor levezetésünk egyszerre adja az összefüggést bármekkora szögekre. Ha ezeket az összefüggéseket felhasználtuk volna, akkor természetesen sokkal rövidebben célhoz értünk volna. Mégis ez a hosszadalmasabb út elemibb volt, hisz végigjárhatták velünk olyanok is, akik trigonometriáról még nem is hallottak és sokkal tanulságosabb is pl. éppen abban, hogy ezeket a goniometriai azonosságokat is közben újra bebizonyítottuk.2V. ö. Elemente der Mathematik. III. köt., 20. l. |