Kezdőlap


Cím:	Ismerkedjünk a komplex számokkal 1.
Szerző(k):	Surányi János
Füzet:	1948/február, 65 - 71. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Olvastátok-e a harmadfokú egyenlet megoldását, a 90., 91., 92. feladatokat? Biztos, sokan elszomorodtatok, különösen, ha a megjegyzést is elolvastátok utána. A harmadfokú egyenletet visszavezettük másodfokúra, azt azután megoldottuk, de egyáltalán nem törődtünk vele, hogy nem negatív-e az a szám, amiből gyököt vontunk, csak éppen ilyenkor új nevet adtunk az egyenlet megoldásának, komplex számokról beszéltünk. De ha a négyzetgyökvonást sikerült is elvégezni, akkor is még valami $ϱ_{2}$ meg $ϱ_{3}$ komplex számokat kevertünk bele a dologba, amiknek szintén 1 a harmadik hatványa, akárcsak az 1-nek magának. Ez még mindig nem lenne baj. Beérhetnénk azzal, hogy a másodfokú egyenletnek nem mindig van megoldása és ha a harmadfokú egyenlet megoldása közben nyert másodfokú egyenletnek van megoldása, akkor a harmadfokúnak egy megoldása van, ha meg nincs, akkor egy sem. Csakhogy ez nem igaz, mert a harmadfokú egyenletnek mindig van (valós) megoldása és a jegyzetben arra figyelmeztettünk, hogy éppen, ha a megoldás közben nyert másodfokú egyenletnek nincs valós gyöke, akkor van a harmadfokúnak három különböző valós gyöke. Sőt, még azt is elmondtuk, hogy ha három különböző valós gyök van, akkor nem is lehet elkerülni ezeket a titokzatos komplex számokat. Ha így van, akkor sem veszett el minden remény: próbáljunk megbarátkozni azokkal a komplex számokkal. Nem is olyan nehéz. Akinek van kedve, tartson velünk.

A valós számok ‐ hogy úgy mondjam ‐ itt élnek közöttünk. Alig van olyan osztozkodás, hogy törtek elő ne kerülnének, s ha mérünk, még az is véletlen, ha a mértékegység valamilyen tört része is, pontosan megvan a mérendőben, így sokkal gyakrabban jutunk irracionális számhoz, mint racinálishoz (persze a gyakorlatban megelégszünk azzal, hogy ,,pontosan'' lemérünk valamit, pl. centiméter, v. milliméter pontossággal egy távolságot, stb.; vagyis beérjük egy alkalmas racionális közelítő értékével a mértékszámnak).
Mégis, hogy találkoztunk velük össze? Hisz valamikor régen, gyerekkorunkban az volt az első matematikai élményünk, hogy az egymástól elválasztható tárgyakat meg tudtuk számlálni, s így az egész számok léteztek még csak számunkra. Hogy jutottunk el a többihez?
Például a negatív számokat akkor fedeztük fel, mikor valami számot keresve, olyan feladathoz jutottunk, ahol egy számból nagyobbat kellene kivonni. Még az is kiderül ilyenkor, hogy a fordított különbség megoldása a feladatnak, csak azt mondja, hogy valami, amit egy másik mennyiségnél nagyobbnak vártunk, valójában kisebb nála. Ha így rájöttünk, hogy az el nem végezhető kivonásnak is van valami értelme, akkor legegyszerűbb megoldásnak az bizonyult, hogy az ilyen különbségeket, mint újfajta számokat, negatív számokat, hozzávettük az ismertekhez. Negatív számokhoz igen gyakran jutunk egyenletek megoldásakor, ott pedig az ismeretlennel úgy számolunk, mielőtt még tudnánk, hogy mennyit jelent, amint azt az algebrában megszoktuk. Akkor van tehát csak jogunk a kapott negatív számokra azt mondani, hogy eleget tesznek a kérdéses egyenletnek, ha sikerül az alapműveleteket a negatív számokra is úgy terjeszteni ki, hogy az algebra számolási szabályai érvényben maradjanak. Ezt a kiterjesztést ebben az esetben annál könnyebb megtalálni, mert könnyű olyan gyakorlati feladatot találni, amiben negatív mennyiségek is szerepelnek és melyek ezért tanáccsal tudnak szolgálni.¹) Most is hasonló dologról van szó, arról, hogy egy bizonyos műveletet ‐ tudniillik a négyzetgyökvonást negatív számokból ‐ a valós számok körében nem tudunk elvégezni, hisz minden valós szám négyzete pozitív szám. Most is azért vezetünk be újfajta számokat, hogy ezt a műveletek is el tudjuk végezni. Természetesen az ezekkel kibővített számkörben is szeretnénk számolni, hiszen például a harmadfokú egyenlet megoldása közben is szükség van arra, hogy a régi és új számokat műveletekkel kapcsoljuk össze és a műveletek eredményeivel újabb műveleteket végezzünk. Első pillanatban még bizonytalanabbul érezzük magunkat, mint mikor a negatív számokkal kellett megbarátkoznunk és mondjuk, negatívot szoroznunk negatívval, mert hirtelen nem találunk olyan gyakorlati problémát, ami utat mutathatna. Egy útmutatónk azért marad: továbbra is az lesz a célunk, hogy úgy lehessen a kibővített számkörben is számolni, mint ahogy az algebrában megszoktuk: például összeg tagjait, szorzat tényezőit felcserélni, tagokat, illetőleg tényezőket egy összegen, illetőleg szorzaton belül, tetszés szerint és az éppen elérendő célnak megfelelően összefoglalni, zárójeleket felbontani, ,,beszorozni'' és ,,kiemelni'', stb.
Ezt persze meg lehet próbálni, de vajon érdemes-e? Nem kell-e majd folyton újra kezdeni a mesterséget, ha az újfajta számokból egyre magasabb gyököt akarunk vonni, úgy, hogy a végén már névvel sem bírjuk a sok számfajtát? Hát megnyugtatlak benneteket előre. Éppen ez az egyik szépsége a dolognak, hogy nem. De erről nem beszélek most többet, hisz aki velem jön erre a kis kirándulásra a számok birodalmába, maga fogja rövidesen bebizonyítani. Persze, előbb alapos ismerkedésre lesz szükség az ilyen csinált, képzeletünkből termett mennyiségekkel, hogy ne idegenkedjünk tőlük. De érdemes az ismerkedés kezdetén fellépő első elfogódottsággal szembenézni, mert ha túljuttok rajta, sok kellemes meglepetést tartogat az új ismerős tarsolyában. Bár látszólag csak algebrai kérdésekkel foglalkozunk, valójában sok geometriai érdekessége is lesz kirándulásunknak.
Tehát szeretnénk a valós számok körét olyan számokkal tovább bővíteni, amelyek a negatív számok négyzetgyökei lennének és azt akarjuk, hogy ezekkel is úgy lehessen számolni, mint az algebrában számolni szoktunk. Egy negatív számból való négyzetgyökvonást, ha az algebrában szokott módon számolunk, félig el is tudunk végezni, pl.

\sqrt[]{- 49} = \sqrt[]{49 \cdot (- 1)} = 7 \cdot \sqrt[]{- 1}

, vagy

\sqrt[]{- 57} = \sqrt[]{57 \cdot (- 1)} = \sqrt[]{57} \cdot \sqrt[]{- 1}

és így kiderül, hogy mindössze egy új számot kell bevezetni, a

\sqrt[]{- 1}

számára. Ezt a számot imaginárius (képzeletbeli) egységnek nevezték el, magyarra képzetesnek fordították,

i

-vel szokás jelölni. Őt tehát az jellemzi, hogy

i^{2} = - 1

. Mindjárt párja is akad, mert ha az algebra számolási szabályai érvényesek, akkor

{(- i)}^{2} = (- i) (- i) = i^{2} = - 1

i

-t összes valós többszöröseivel együtt, mint pl. a már szerepelt bővítést,

7 i

\sqrt[]{57 i}

, nevezzük képzetes számoknak. Annyit tudunk róluk, hogy a négyzetük negatív szám, így ők nem tartozhatnak semmiképp sem a valós számok közé, mert azoknak viszont pozitív a négyzetük. Egy valós szám azért közéjük lopódzott,

i

0-szorosán is természetesen 0-t értünk. Egyébként összeadhatjuk, kivonhatjuk őket nyugodtan egymás közt hasonlóan, mint a valós számokat. Úgy látszik, mintha rendben is volnánk. A szorzásnál nem lesz semmi nehézségünk, összeadni is tudunk már valósakat is, képzeteseket is. De mit értsünk egy valós, meg egy képzetes szám összegén? Érthetünk-e valós számot? Ha pl.

3 + 2 i = 4

volna, ez elsőfokú egyenlet

i

számára. Megoldva,

i = \frac{1}{2}

-et, tehát valós számot kapnánk. Arról pedig már meggyőződtünk, hogy ez lehetetlen, hiszen sem

\frac{1}{2}

-nek, sem más valós számnak négyzete nem lehet

- 1

. De ugyanígy nem lehet

3 + 2 i

képzetes sem. Ha pl.

3 + 2 i = 4 i

volna, ebből meg

i = \frac{3}{2}

következnék, ami éppúgy lehetetlen. Nincs más hátra, mint még nagyobbra méretezni a bővítést, a

3 + 2 i

-t is, meg minden olyan számot, amely egy valós, meg egy képzetes szám összeadásából keletkezik, új számként venni hozzá az eddigiekhez. Az ilyen számokat komplex számoknak nevezzük.
Hogy ki tudjuk magunkat ismerni a bővített számkörben, próbáljuk meg új számainkat geometriailag ábrázolni, mert a valós számokat is jobban el tudtuk képzelni, ha a számvonalon ábrázoltuk őket. Ez úgy történt, hogy kijelöltünk a számvonalon, vagy ahogy ezentúl nevezni fogjuk, a valós tengelyen egy

O

pontot ‐ ennek felelt meg a 0 szám ‐ és választottunk egy mértékegységet. Az

O

ponttól egyik irányban a pozitív számokat ábrázoltuk; mindegyiket azzal a ponttal, mely az

O

ponttól, a választott mértékegységgel mérve, olyan távolságra van, mint a kérdéses pozitív szám. Az ellenkező irányban pedig a negatív számokat ábrázoltuk, mindegyiket olyan messze az

O

ponttól, mint amekkora az abszolút értéke. A képzetes számokkal megtölthetünk egy másik számvonalat: a képzetes tengelyt. Ezt a másik tengelyt célszerű úgy választani, hogy az

O

pontban messe a valós tengelyt, hiszen az

O

-nak mindkét tengelyen rajta kell lennie. Az a szokás, hogy képzetes tengelynek az

O

pontban a valós tengelyre emelt merőlegest választjuk és azon is ugyanazt az egységet használjuk, mint a valós tengelyen; azaz azokat a képzetes számokat, amelyek az

i

-nek pozitív számmal való szorzásával keletkeztek, az egyik irányban, a többieket pedig az ellenkező irányban ábrázoljuk a képzetes tengelynek azzal a pontjával, amely az

O

ponttól, a választott egységgel mérve, olyan messze van, mint az

i

együtthatójának abszolút értéke a kérdéses számban. Ezek után a komplex számok ábrázolása sem okoz gondot. Kínálkozik például

3 + 2 i

számára az a pont (28. ábra), amelybe úgy jutunk, hogy a valós tengelyen 3 távolságra megyünk el és utána a képzetes tengely irányában 2 távolságra. (Persze, ha a két utat fordított sorrendben tesszük meg, akkor ugyanabba a pontba jutunk.)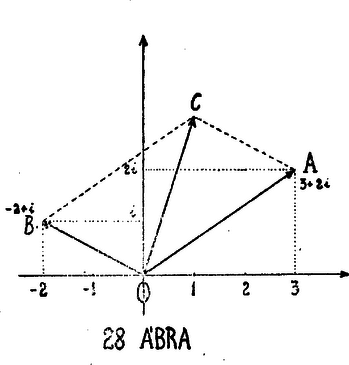

Hasonlóan ábrázolhatjuk a többi komplex számot is; együtt (a valós és képzetes számokat is beleértve) egy síkot töltenek ki, az u. n. számsíkot.
A komplex számban szereplő valós összeadandót, példánkban a 3-at, a komplex szám valós részének, a képzetes összeadandóban pedig

i

együtthatóját, példánkban a 2-t (

i

nélkül) a szám képzetes részének nevezzük. Ezek számára külön jelölést is használunk. Ha egy német

Re

-et (a reális szó kezdete), vagy

Im

-t (imaginárius) írunk a komplex szám elé, az a valós, illetőleg képzetes részét jelenti a számnak. Különösen akkor használjuk, ha a komplex szám egy betűvel van jelölve. Nevezzük el pl.

3 + 2 i

-t

z

-nek, akkor

Re (z) = 3

Im (z) = 2

. Ha

w

jelenti a

3 - 2 i

számot, akkor

Re (w) = 3

Im (w) = - 2

;

Re (i) = 0

Im = 1

.
A komplex számok közt persze speciális esetként ott szerepelnek a valósok is (olyan komplex számok, melyek képzetes része 0) és a képzetesek is (ezeknek meg a valós része 0).
Ha két komplex számot az algebra törvényei szerint összeadunk, pl.

\begin{matrix} (3 + 2 i) + (- 2 + i) = (3 - 2) + (2 i + i) = 1 + 3 i, \end{matrix}

akkor ismét egy komplex számot kapunk. Ha tehát azt akarjuk, hogy az algebra törvényei érvényben maradjanak, akkor komplex számokat mindig így kell összeadni, akármilyen számok is kerülnek a 3 és 2, meg a

- 2

és 1 helyére. Az összeg az a komplex szám lesz, amelynek a valós része a két összeadandó valós részének az összege, képzetes része meg a képzetes részek összege. Fogalmazzuk meg egyszer az algebra nyelvén is: jelképezze

z_{1} = x_{1} + y_{1} i

akármelyik komplex számot, meg

z_{2} = x_{2} + y_{2} i

is egy tetszőlegest, akkor:

\begin{matrix} z_{1} + z_{2} = (x_{1} + x_{2}) + (y_{1} + y_{2}) i \end{matrix}

(1)

Nézzük meg, mit jelent az összeadás geometriailag? Jelöljük a

3 + 2 i

- 2 + i

komplex számokat és az összegüket ábrázoló pontokat

A

B

C

-vel akkor az

A C

szakasz párhuzamos

O B

-vel.

O A C B

parallelogramma s így egyben

B C

is párhuzamos és egyenlő

O A

-val. Könnyebb lesz ezért kifejezni magunkat, ha a komplex számokat az

O

-tól a számot ábrázoló pontig húzott vonaldarabbal jellemezzük. Ilyen irányított vonaldarabokat jól lehet használni a geometriában (térben is); vektor-nak szokás nevezni. Egy komplex számot tehát hol egy ponttal, hol az

O

ponttól hozzá húzott vektorral fogjuk jelképezni. A kettő között lényeges különbség nincs, így nyugodtan használhatjuk mindig azt, amelyik kényelmesebb. Ne lepődjünk hát meg, ha ugyanazt egyszer, mint a

3 + 2 i

számot, egyszer, mint a

3 + 2 i

vektort, vagy a

3 + 2 i

pontot emlegetünk. Mindig ugyanarról van szó, csak különböző módon való szemléltetésre utalunk.
Az összeadást vektorokkal elmondva: ha az egyik szám vektorának a végpontjából rakjuk fel a másik szám vektorát irány és nagyság szerint, akkor az utóbbinak a végpontja (vagy, ha tetszik, a kezdőponttól hozzá húzott vektor) ábrázolja az összeget. Ez független a tagok sorrendjétől. Világos ez az (1) kifejezésből is. Geometriailag meg abból, hogy ha ellenkező sorrendben is felrajzoljuk a vektorokat egymásután, akkor egy parallelogrammát kapunk, hasonlóan, mint az 1. ábrán, amelynek az

O

-ból kiinduló átlója az összeg.
Most hagyjátok egy kicsit abba az olvasást, fogjatok papírt, ceruzát és gyakorlásul oldjátok meg a következő feladatokat. A sorszámmal ellátottakkal pontot is lehet szerezni. ‐ Ábrázoljátok a következő pontokat:

5 - 2 i

- 3 \frac{1}{2} - \frac{7}{6} i

2 \cdot 3 + 3 \cdot 2 i

- 11 + 6 \cdot 8 i

z_{1}

és

z_{2}

legyen a komplex számsík két különböző pontja. Írjuk fel a

\vec{z_{1} z_{2}}

vektorhoz tartozó komplex számot. (A fölé rajzolt nyíllal azt jelöljük, hogy a vektor

z_{1}

-től

z_{2}

-höz mutat.)
Egy téglalap középpontja az

O

pont, oldalai a tengelyekkel párhuzamosak és egyik csúcsa

z_{1} = - 5 + 2 i

, írjuk fel a többi csúcsát!
Egy szabályos hatszög középpontja

i

, egyik csúcsa

O

. Mik a többi csúcsai?
1. Milyen hosszúak az

1 - \sqrt[]{3} i

2 i

- 1 - \sqrt[]{3} i

háromszög oldalai?
2. Egy rombusz egyik oldala a

z_{0} = x_{0} + y_{0} i

vektor. Egyik átlója

45^{\circ}

-os szöget zár be az

x

tengellyel. Írjuk fel a másik két csúcsát. Számítsuk ki őket, ha

x_{0} = 3

y_{0} = 4

.
3. Keressünk a

9 \cdot 2 - 3 \cdot 6 i

-hez olyan komplex számot, hogy összegük valós, különbségük képzetes legyen. Található-e ilyen bármely

z = x + y i

számhoz és melyik az? Geometriailag mi jellemzi ezt a számot?
A

z

szám ilyen társát a hozzá konjugált komplex számnak, röviden

z

konjugáltjának szokás nevezni és külön jelet is vezettek be rá:

\bar{z}

. (Szokás néha

z^{*}

-gal is jelölni. Mi az előbbit fogjuk használni.) Egy komplex szám és a konjugáltja közötti viszony kölcsönös: mindegyiknek a másik a konjugáltja, ezért a két számot együtt, egymáshoz konjugált, vagy röviden konjugált komplex számoknak nevezzük.
4. A konjugált jelével írjuk fel egy komplex szám valós, képzetes részét; jellemezzük a valós számokat. 5. A

z = x + y i

komplex számokhoz tartozó vektor hosszát a

z

komplex szám abszolut értékének nevezzük és

| z |

-vel jelöljük. Mutassuk meg, hogy ha

z

valós, akkor

| z |

a régi értelemben vett abszolút érték. Írjuk fel általában

| z |

-t

x

és

y

segítségével.
6. Az előbbi feladat jelöléseit használva, mutassuk meg, hogy

\begin{matrix} | x | + | y | \geq | z | \geq \frac{| x | + | y |}{\sqrt[]{2}} \end{matrix}

¹Lásd pl. Péter Rózsa: Játék a végtelennel. II. rész, 9. fej., különösen 111‐114. oldal.