Cím:	A számok hatványainak összegéről 2.
Szerző(k):	Kalmár László
Füzet:	1947/december, 39 - 47. oldal	PDF  |  MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. IV.   Remélem, sokan megcsináltátok azóta a piramist kartonpapírból. Kicsit körülményes volt talán az összeragasztása, de annál nagyobb izgalommal vártátok, hogy kész legyen mind a három, mi lesz belőlük, ha összerakjátok. Egyet meghagytatok ,,rendes'' helyzetben, hogy vízszintes maradjon a négyzetes lapja. A másikat oldalra fektetve mellé raktátok, ahogy a 17. ábra mutatja, hogy a hegyén magában álló kocka az álló mellé kerüljön, a négyzetes lapja meg függőlegesen álljon. 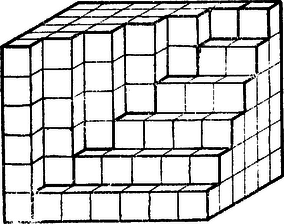    Hátul két fogazott lapból már téglalap lett. Az üres helyre megpróbáltátok beilleszteni a harmadik piramist, oldalra fektetve. Igen ám, de egy kis baj van, mert nem illett bele. Ha úgy állítottátok, hogy oldalt semmi ki ne álljon, akkor a tetején egyre mélyebb lyukak maradtak, ha meg összetoltátok, mint az ábrán is látható, akkor eltűntek a lyukak, de oldalt maradt egykockányi szélességű lépcső. 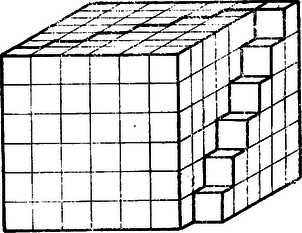    Még három piramis kell hát, hogy hiánytalan hasábot alkossunk; azokat is ugyanígy kéne összeraknunk, s az egészet felfordítva az előbbi idom mellé tennünk. 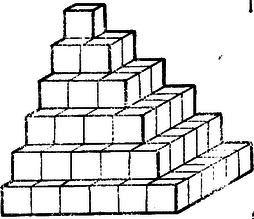    Nem tudom, hányótokat ihletett ez a meglátás arra, hogy még három piramist ragasszatok kartonpapírból; de akit vissza tartott a ragasztás nehézsége, az is jól el tudja képzelni, ugye, hogy hat piramisból olyan hasábot tudunk összerakni, amelynek magassága 6, szélessége 7, hossza meg 13 kockányi, azért 13, mert két 6‐6 kockányi réteg közé került a két lépcsőből összerótt 1 kockányi réteg. Ha nem $6\cdot 6$ kockából állna a piramis legalsó rétege, hanem $100\cdot 100$-ból, akkor 7 helyett 101 kockányi lenne a hat piramisból keletkező hasáb szélessége, 6 helyett 100 a magassága és 13 helyett $100+1+100=201$ a hossza; tehát $101\cdot 100\cdot 201$, vagyis $2030100$ kockából állana; ebből egy piramisra hatodrész annyi, $338350$ kocka esnék. Azaz $1^2+2^2+3^2+\text{...}+{100}^2=338350$ és azt a 6-ot, amely 100-at is jelképezhet, algebrai szokás szerint $n$-nel, azt a 7-et, amely 101 lesz, ha a 6 100-at jelképez, $\left(n+1\right)$-gyel, azt a 13-at meg, amely 201 lesz, ha a 6 100-at jelképez, s mindig kétszerannyi meg még egy, mint ami a 6 helyett áll, $\left(2n+1\right)$-gyel jelölve, $\begin{array}{c}{\displaystyle 1^2+2^2+3^2+\text{...}+n^2=\frac{n\left(n+1\right)\left(2n+1\right)}{6}\mathrm{.}}\end{array}$   V.   No de most, ha azt kérdezem, mennyi az első 100, az első $n$ szám köbének összege, mi lesz? A számok első hatványainak összegzése geometriai nyelvre lefordítva, síkbeli feladat lett; ott azonnal láttuk, mi lesz a fogazott háromszögből, ha megfordítva fölé teszünk még egy példányt belőle. A második hatványok összegzéséhez tér kellett; ott már nagyon meg kellett erőltetnünk fantáziánkat, vagy kartonpapír modellel segítenünk, hogy lássuk, mi lesz a piramisból, ha hármat összeteszünk belőle. A számok harmadik hatványának összegzéséhez talán csak nem a négydimenziós térbe kell mennünk? Ott aztán már teljesen vakok vagyunk; el sem tudjuk képzelni, milyen lehet egy négydimenziós tér, ha volna. Hát még, hogy milyen lenne benne a kocka megfelelőiből, az ,,oktatop''-okból összerakott négydimenziós térbeli gúla. Azt meg aztán még úgy sem, hogy négy ilyen gúlát hogyan kell összeraknunk, hogy négydimenziós térbeli hasábféle legyen belőle, meg hogy e hasábféle tetején micsoda fogazott cifraság fog megjelenni. Látjátok, az algebra nyelvének is megvan a maga előnye, a mértanénak is. A mértan nyelve szemléletes, ha mértani nyelven gondolkodunk, látjuk mit csinálunk valójában, mit miért csinálunk. De ez a szemléletesség csak három dimenzióig terjed, aztán egyszerre megszűnik. A négy és több dimenziós mértan nyelve eredetileg nem is tartozott hozzá a mértan nyelvéhez; valami nyelvújításfélével keletkezett, hogy olyan dolgokat is el lehessen mondani a mértan nyelvén, amiket addig nem lehetett. De minden nyelvújításnak megvan az a hátránya, hogy a szemléletesség rovására megy. Régi magyar nyelvünk is mennyivel szemléletesebb volt, mint a mostani, ha egy‐két elvont fogalomnak a kimondására kevésbé is volt talán alkalmas. Viszont az algebra nyelvén nem okoz semmi nehézséget a dimenziószám emelése: csak a hatványkitevők lesznek magasabbak. No de mi most még csak a problémánkat tudjuk elmondani algebrául, a megoldást csak geometriául tudjuk. Nem lehetne azt is visszafordítani most már, hogy megtanultuk, algebrára, hogy aztán könnyebben tudjunk általánosítani magasabb kitevőkre is? Vagy ha ezt a megoldást nem is, nem tudnánk más számlálósabb, s így algebrára könnyebben lefordítható megoldást találni? A matematikus szeret gondolkodni, de mindig csak új dolgokon. Amit egyszer már átgondolt, azt szereti magának elraktározni (hiszen erre valók pl. a képletek is), hogy ne kelljen mindig újra meg újra átgondolnia. Szeret a már átgondolt dolgok kész eredményére hivatkozni. Ha valami új feladat előtt áll, igyekszik azt valami régebbi, már átgondolt feladatra vissza vezetni, hogy annak kész végeredményére hivatkozhassék. Nem lustaságból nem gondolja végig újra, hanem azért, hogy több energiája jusson mindig újabb és újabb problémákon gondolkodni. Még anekdota is szól róla: persze üres fazékban a matematikus is úgy forral vizet, hogy vizet önt bele, azután felteszi a tűzre. Ha azonban vízzel teli fazék van előtte, akkor kiönti, hogy ezzel visszavezesse a feladatot arra, amit az előbb már megoldott. A mi piramisunkkal kapcsolatban is azt kérdezi a vérbeli matematikus: ha már egyszer nagy nehezen, így vagy úgy, átgondoltam, hogy lehet három gúlából hasábot csinálni, nem lehet-e elkerülni, hogy most ugyanezt átgondoljam a piramisokkal kapcsolatban is; nem lehet-e visszavezetni a piramis kockái számának (tehát köbtartalmának) kérdését a gúla köbtartalmára? Lássuk először a megfelelő kérdést a síkban. Ahelyett, hogy a fogazott háromszöggel ugyanazt csináltuk, mint a sima háromszöggel, t. i. hogy fordítva mellé tettük, nem lehetne-e visszavezetni a fogazott háromszög területének kérdését a sima háromszögére? Azonnal látjuk, hogy lehet. Kétféleképpen is. Vagy levágjuk a háromszög kiálló fogait szép simára, vagy úgy, mint a 18. ábra mutatja, hogy kitoldjuk kis háromszögekkel sima háromszöggé.     A földszintre is, minden emeletre is kell egy‐egy ilyen kis derékszögű háromszög, meg még tetőnek is egy, tehát eggyel több, mint ahány kis négyzetnyi magas a fogazott háromszög. A kis négyzetek oldalát választva egységnek, egy‐egy kis háromszög területe ${}^1{/}_2$, mert kettő tesz ki belőle egy‐egy kis négyzetet. Fogazott háromszögünk területe (ha egy‐egy befogója mentén $n$ kis négyzet van) $\left(n+1\right)$ ilyen kis félnégyzettel együtt $\frac{{\left(n+1\right)}^2}{2}$ lesz (mert alapja is, magassága is megnövekszik 1-gyel), tehát azok nélkül $\frac{{\left(n+1\right)}^2}{2}-\left(n+1\right)\cdot \frac{1}{2}=\frac{{\left(n+1\right)}^2-\left(n+1\right)}{2}=\frac{\left(n+1\right)\left(n+1-1\right)}{2}$, vagyis $\frac{\left(n+1\right)n}{2}$ a területe, ennyi tehát az első $n$ szám összege. (Akinek így, $n$-nel, nehéz, gondolja át 6-tal, aztán azt, hogyan módosul mindez, ha 6 helyett 10, vagy 100 kis négyzetnyi a fogazott háromszög szélessége és magassága, aztán rájön, hogy kell azt, amit tapasztalt, $n$-nel leírni.) Hasonlóan vissza vezethetjük piramisunk köbtartalom számítását is a gúláéra. Nézzétek meg újra a piramis ábráját; könnyen elképzelhetitek, hogyan lehet azt gúlává kiegészíteni. Tetejének teszünk egy kis gúlát, amelynek alapja épp a legfelső kis kocka fedőlapja, egyik oldaléle pedig ‐ a a piramis ábráján a bal hátsó ‐ merőleges rá s a hossza megegyezik a kocka élével; szóval olyan kis gúlát, amilyenből három egyforma tesz ki egy kis kockát. (19. ábra.) 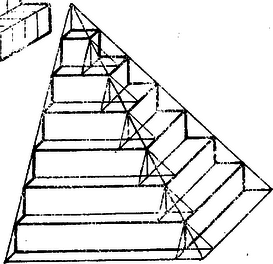    Ugyanilyen kis harmadkockányi gúlát teszünk minden egyes emeleten a sarokkocka tetejére s a földszinten is a sarokkocka mellé, úgy, hogy függőleges éle a sarokélre essék, függőleges lapjai meg a piramis földszinti kockáinak a sarokélbe összefutó lapjai meghosszabbítását alkossák. Még egy‐egy prizma hiányzik minden emeleten és a földszinten is, hogy gúla legyen a piramisból. A legfelső emeleten olyan prizmák hiányoznak, amelyek úgy keletkeznek a kis kockákból, hogy egy átlósíkja mentén kettévágjuk; az alatta levő emeleten két‐két ilyen félkockányi prizma kell a sarokra tett kis gúla mindkét oldalára, a még alatta levő emeleten három‐három félkockányi prizma, s. i. t. Így olyan gúla lesz a piramisból, amelynek alapéle is magassága is eggyel nagyobb, mint a piramisé; ábránkon 7, általában, ha $n^2$ kis kockából állt a piramis legalsó rétege, $\left(n+1\right)$. Eszerint a kapott gúla alapterülete ${\left(n+1\right)}^2$ kockalap, s így a gúla köbtartalma $\frac{{\left(n+1\right)}^2\left(n+1\right)}{3}=\frac{{\left(n+1\right)}^3}{3}$ kis kocka. A piramis köbtartalmát megkapjuk, ha elvesszük belőle a kis gúlákat és a prizmákat, amiket hozzátettünk. Kis gúla $\left(n+1\right)$ van: tetőnek is egy, minden emeletre is egy, s a földszintre is egy jutott; köbtartalmuk együtt $\frac{n+1}{3}$. A tető kivételével mindegyik kis gúla két oldalára jutottak prizmák; ha ezeket összetesszük, a legfelső emeleten 1, az alatta levőn 2, a még alatta levőn 3 kis kocka lesz belőlük s. i. t., a földszinten meg $n$, így összesen $1+2+3+\text{...}+n=\frac{n\left(n+1\right)}{2}$ kis kocka a köbtartalmuk. A nagy gúla köbtartalmából kivonva a kis gúlákét is, a prizmákét is, megkapjuk a piramis köbtartalmát: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{{\left(n+1\right)}^3}{3}-\frac{n+1}{3}-\frac{n\left(n+1\right)}{2}=\frac{2{\left(n+1\right)}^3-2\left(n+1\right)-3n\left(n+1\right)}{6}=}\hfill \\ \hfill {\displaystyle =\frac{\left(n+1\right)\left[2{\left(n+1\right)}^2-2-3n\right]}{6}=\frac{\left(n+1\right)\left(2n^2+n\right)}{6}=\frac{\left(n+1\right)n\left(2n+1\right)}{6}\mathrm{.}}\hfill \end{array}}$ Ennyi hát az első $n$ négyzetszám összege.   VI.   Szép, szép, mondjátok, ez is egy levezetés a már más módon megkapott képletre, könnyebben is el lehet képzelni a piramis kiegészítését gúlára, mint a három különböző helyzetű piramis összerakását; de mivel jutottunk közelebb a köbszámok összegezéséhez? Miért lehetne ezt a kiegészítéses geometriai meggondolást könnyebben lefordítani az algebrára, mint az összerakásokat? Megmondom őszintén: az összerakásokat is le lehet fordítani algebrára. A piramis forgatásának az felel meg, hogy más sorrendben számláljuk meg a kockákat s ennek valami olyasmi, hogy egy bizonyos összeg tagjait más sorrendben adjuk össze. De azt, hogy milyen sorrendben, megint csak geometriailag lehet áttekinthetően megmondani; s emiatt az így kapható algebrai bizonyítás sem alkalmazható akármilyen kitevőjű hatványok összegezésére. A kiegészítéses bizonyításban ezzel szemben a piramis helyzete marad a régiben, tehát a tagok sorrendjét nem változtatjuk, csak minden emeleten, algebrai nyelven: minden tagban végzünk valamilyen átalakítást. Lássuk, milyet. Nézzük először az egyszerűbbik esetet a fogazott háromszög kiegészítését simára. Itt is beszélhetünk emeletekről; számozzuk őket a szokástól eltérőleg felülről lefelé. Az első emeleten hát egy négyzet van, a másodikon kettő stb.; a tetőt, ha tetszik, 0-dik emeletnek nevezhetjük. Nos nézzük meg általában, mi történt a $k$-adik emeleten, ahol $k$ lehet 0, 1, 2, $\text{...}$, egészen $n$-ig. Itt volt $k$ kis négyzet, hozzátettünk egy kis háromszöget, lett belőle egy trapéz; s a $k$ kis négyzetet megkapjuk, ha a trapézból levonjuk a kis háromszöget. A trapéz alapja $\left(k+1\right)$, teteje $k$, magassága 1 egységnyi, ha megint a kis négyzet oldalát választjuk egységnek. A trapéz területe tehát: $\frac{k+1+k}{2}$. A $k$-adik emeleten történt átalakításnak tehát a $\frac{k+1+k}{2}-\frac{1}{2}=k$ azonosság felelne meg algebrai nyelven.   Nem egészen jó a fordítás. Az ábráról világos, hogy a különböző emeleteken levő trapézok (meg a 0-adik emeleten levő kis háromszög) együttvéve a nagy háromszöget adják. Az ellenben nem világos, hogy ha $\frac{k+1+k}{2}$-ben $k$ helyébe a 0, 1, 2, $\text{...}$, $n$ értékeket tesszük és összegezünk, a nagy háromszög területét $\frac{{\left(n+1\right)}^2}{2}$-t kapjuk. Úgy látszik, megint szó szerint fordítottunk. Pedig az a jó fordítás, amely ugyanolyan világosan mutatja az összefüggéseket, mint az eredeti.   Így hát a trapézt nem trapéznak fogjuk fordítani, hanem ,,csonka háromszögnek''. Annál jobb ez, mert hiszen a piramis $k$-adik emeletén is csonka gúla van, abból meg négyzetes hasáb lesz, ha elvesszük belőle a kis gúlát, meg a két prizmát. Csonka háromszög: nagy háromszög, elvéve belőle egy kisebb, hasonló háromszöget. A $k$-adik emeleten s a fölötte levő emeleteken együtt olyan háromszög van, amelynek alapja is, magassága is $\left(k+1\right)$ egységnyi, hiszen ennyi volt a trapéz alapja, s a 0-adiktól a $k$-adikig $\left(k+1\right)$ emelet van, mindegyik egységnyi magas. Ugyanígy a $k$-adik emelet fölötti emeleteken együtt olyan háromszög van, amelynek alapja is, magassága is $k$ egységnyi. A trapéz, azaz a csonka háromszög helyes fordítása tehát: $\frac{{\left(k+1\right)}^2}{2}-\frac{k^2}{2}$, s azé az átalakításé, ami a $k$-adik emeleten történt, a következő azonosság: $\begin{array}{c}{\displaystyle k=\frac{{\left(k+1\right)}^2}{2}-\frac{k^2}{2}-\frac{1}{2}\mathrm{.}}\end{array}$ Ezt az azonosságot persze minden geometria nélkül, algebrailag is igazolhatjuk, pl. úgy, hogy a ${\left(k+1\right)}^2=k^2+2k+1$ egyenletből kifejezzük a vastag betűvel nyomott $k$-t. Nos, most már megy a fordítás, mint a karikacsapás. Tegyünk ebbe az azonosságba $k$ helyébe 0-t, 1-et, 2-t, 3-at, 4-et, 5-öt és 6-ot, akkor felírtuk algebrai nyelven, mi történt sorra a 0-adik, első, második, harmadik, negyedik, ötödik, és hatodik emeleten (most a hatodik emeletnek a földszintet neveztük): ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 0}& {\displaystyle =\frac{1^2}{2}-\phantom{mmii}\frac{1}{2}\mathrm{,}}\hfill \\ \hfill {\displaystyle 1}& {\displaystyle =\frac{2^2}{2}-\frac{1^2}{2}-\frac{1}{2}\mathrm{,}}\hfill \\ \hfill {\displaystyle 2}& {\displaystyle =\frac{3^2}{2}-\frac{2^2}{2}-\frac{1}{2}\mathrm{,}}\hfill \\ \hfill {\displaystyle 3}& {\displaystyle =\frac{4^2}{2}-\frac{3^2}{2}-\frac{1}{2}\mathrm{,}}\hfill \\ \hfill {\displaystyle 4}& {\displaystyle =\frac{5^2}{2}-\frac{4^2}{2}-\frac{1}{2}\mathrm{,}}\hfill \\ \hfill {\displaystyle 5}& {\displaystyle =\frac{6^2}{2}-\frac{5^2}{2}-\frac{1}{2}\mathrm{,}}\hfill \\ \hfill {\displaystyle 6}& {\displaystyle =\frac{7^2}{2}-\frac{6^2}{2}-\frac{1}{2}\mathrm{.}}\hfill \end{array}}$ Az egyes emeletek egymás fölött vannak; ennek algebrai nyelven az felel meg, hogy ennek a hét egyenlőségnek bal- és jobb oldalát összeadjuk. A baloldalon $1+2+3+4+5+6$-ot kapunk, a jobboldalon $1^2/2$, $2^2/2$, $3^2/2$, $4^2/2$, $5^2/2$ és $6^2/2$ mind kiesnek, csak $7^2/2$ marad meg (a nagy háromszög területe!), kivonva belőle 7-szer $1/2$-et (a hét kis háromszög területét!). Ha nem 6-ig, hanem $n$-ig mentünk volna a $k$ helyébe való helyettesítésben, akkor a $7^2/2$ helyett ${\left(n+1\right)}^2/2$ maradt volna meg s nem 7-szer, hanem $\left(n+1\right)$-szer $1/2$-et kellett volna levonnunk belőle, s azt kaptuk volna, hogy $\begin{array}{c}{\displaystyle 1+2+3+\text{...}+n=\frac{{\left(n+1\right)}^2}{2}-\frac{n+1}{2}=\frac{\left(n+1\right)n}{2}\mathrm{.}}\end{array}$ Nos, ugyanígy lefordíthatjuk algebrai nyelvre azt a geometriai okoskodást is, amikor a piramist egészítettük ki gúlára. Nézzük, mi történt ott a (felülről számított) $k$-adik emeleten? A $k$ alapélű, 1 magasságú négyzetes hasábot két, egyenként $k$ félkockából álló prizmával és egy harmadkockányi gúlával kiegészítettük olyan csonka gúlává, amelynek alapja $\left(k+1\right)$ oldalhosszú, fedele $k$ oldalhosszú négyzet, magassága pedig 1. E csonka gúla köbtartalmát megint ne a szokott köbtartalom képlettel fordítsuk le algebrai nyelvre, mert akkor megint nem látszik, hogy a csonka gúlák együtt gúlát adnak, hanem úgy fogjuk fel a csonka gúlát, hogy a $\left(k+1\right)$ alapélű, $\left(k+1\right)$ magasságú gúlából keletkezett, ha elhagytuk belőle a $k$ alapélű, $k$ magasságú gúlát. A $k$-adik emeleten levő csonka gúla köbtartalma tehát $\frac{{\left(k+1\right)}^3}{3}-\frac{k^3}{3}$, s annak, hogy az eredeti $k$ alapélű, 1 magasságú négyzetes hasábot úgy kapjuk meg, hogy ebből elvesszük a $2k$ félkockányi prizmát, meg a harmadkockányi kis gúlát, algebrai fordítása a $\begin{array}{c}{\displaystyle k^2=\frac{{\left(k+1\right)}^3}{3}-\frac{k^3}{3}-k-\frac{1}{3}}\end{array}$ azonosság. Ha ebben $k$ helyébe sorra 0-t, 1-et, 2-t, 3-at, 4-et, 5-öt és 6-ot teszünk, leírtuk algebrai nyelven, mi történt az egyes emeleteken: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 0^2}& {\displaystyle =\frac{1^3}{3}\phantom{mmmmii}-\frac{1}{3}\mathrm{,}}\hfill \\ \hfill {\displaystyle 1^2}& {\displaystyle =\frac{2^3}{3}-\frac{1^3}{3}-1-\frac{1}{3}\mathrm{,}}\hfill \\ \hfill {\displaystyle 2^2}& {\displaystyle =\frac{3^3}{3}-\frac{2^3}{3}-2-\frac{1}{3}\mathrm{,}}\hfill \\ \hfill {\displaystyle 3^2}& {\displaystyle =\frac{4^3}{3}-\frac{3^3}{3}-3-\frac{1}{3}\mathrm{,}}\hfill \\ \hfill {\displaystyle 4^2}& {\displaystyle =\frac{5^3}{3}-\frac{4^3}{3}-4-\frac{1}{3}\mathrm{,}}\hfill \\ \hfill {\displaystyle 5^2}& {\displaystyle =\frac{6^3}{3}-\frac{5^3}{3}-5-\frac{1}{3}\mathrm{,}}\hfill \\ \hfill {\displaystyle 6^2}& {\displaystyle =\frac{7^3}{3}-\frac{6^3}{3}-6-\frac{1}{3}\mathrm{,}}\hfill \end{array}}$ s ha mindezt összeadjuk, lefordítottuk algebrára, hogy a piramis nem más, mint a nagy gúla, elvéve belőle az egyes emeleteken hozzátett prizmákat és kis gúlákat: $\begin{array}{c}{\displaystyle 1^2+2^2+3^2+4^2+5^2+6^2=\frac{7^3}{3}-\left(1+2+3+4+5+6\right)-\frac{7}{3}\mathrm{,}}\end{array}$ s a jelképes 6-ot $n$-nel, a 7-et $\left(n+1\right)$-gyel pótolva, $\begin{array}{c}{\displaystyle 1^2+2^2+3^2+\text{...}+n^2=\frac{{\left(n+1\right)}^3}{3}-\left(1+2+3+\text{...}+n\right)-\frac{n+1}{3}\mathrm{,}}\end{array}$ amiből már egyszer kiszámítottuk, hogy jön ki az $\frac{n\left(n+1\right)\left(2n+1\right)}{6}$. Persze, ha az egész számítás kulcsát, a $k^2=\frac{{\left(k+1\right)}^3}{3}-\frac{k^3}{3}-k-\frac{1}{3}$ azonosságot, másképpen nem kaphatnánk meg, minthogy geometriából fordítjuk le algebrára, akkor megint nem sokat érnénk az egésszel. De szerencsére az ilyen fajta azonosságokat, amelyekben csak a négy alapművelettel összetett kifejezések vannak kétoldalt, amennyiben igazak, algebrailag is lehet igazolni. De könnyű rájönni is a fenti azonosságokra, úgy, hogy a jól ismert $\begin{array}{c}{\displaystyle {\left(k+1\right)}^3=k^3+3k^2+3k+1}\end{array}$ azonosságot megoldjuk $k^2$-re nézve. Ezek után, azt hiszem, senkinek sem okoz nehézséget az első 100 vagy $n$ természetes szám köbének, vagy negyedik hatványának összegzése sem. Hiszen a ${\left(k+1\right)}^2=k^2+2k+1$, ${\left(k+1\right)}^3=k^3+3k^2+3k+1$ azonosságoknak megvan a megfelelőjük minden kitevőre. Persze a régi görögök módján, ahogyan az ${\left(a+b\right)}^2=a^2+2ab+b^2$ képletet átgondoltuk, csak az ${\left(a+b\right)}^3$ képletére tudnánk még geometriai nyelven rájönni: de mi szerencsére tudunk algebrát is, és így tudjuk, nem kell mást csinálnunk, mint $\left(a+b\right)$-vel ill. $\left(k+1\right)$-gyel ,,beszoroznunk'' s megkapjuk a következő szükséges azonosságot. Nos, akinek sikerül ezekután az első $n$ szám köbének, negyedik, ötödik, hatványának összegére olyan képletet kapni, amelynek segítségével könnyűszerrel ki tudja számítani az első 100 szám köbének, negyedik, ötödik hatványának összegét, írja meg nekem. Az is, aki más úton is meg tudja kapni ezeket a képleteket, legalábbis egyikét‐másikát. Szeretném, ha a következőkön is gondolkodnátok és megírnátok nekem, mire jutottatok. 1. Hogyan lehet a számok négyzetgyökének azt a kiszámítását lefordítani algebrai nyelvre, amely azon alapult, hogy a hat piramist összeraktuk hasábbá? 2. Persze abból is kijön a számok négyzetösszege, hogy három piramist össze lehet rakni olyan hasábbá, amelynek az oldalán van még az a már említett cifraság. Hogyan? Hát ez a geometriai okoskodás hogyan szól algebrául? 3. Hát abból, hogy a három piramist olyan négyzetes hasábbá is össze lehet rakni, amelynek a tetején különböző mélységű lyukak vannak, hogyan jön ki a számok négyzetösszege? Hát ezt a geometriai meggondolást hogyan fordítanátok le algebrára? 4. Ki tudnátok-e hozni legalábbis a számok köbei összegének képletét az e fordítások útján keletkező algebrai okoskodások valamelyikének megfelelőjével? Minél több választ szeretnék kapni!