Cím: A számok hatványainak összegéről 1.
Szerző(k):  Kalmár László 
Füzet: 1947/november, 5 - 10. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I.
 

Ha megkérdezném tőletek, mennyi az első 100 (pozitív egész) szám összege, biztosan sokan mondanátok: ,,Ez igazán könnyű feladat! Számtani sor, Sn=n(a1+an)2=100(1+100)2=50⋅101=5050.'' De én ravasz ember vagyok. Úgy szoktam kipróbálni, megértette-e valaki a másodfokú egyenlet megoldásának gondolatát, hogy olyan harmadfokú egyenletet adok neki, amit ugyanazzal a gondolattal lehet megoldani. Most is zavarba hozom azt, aki csak a képletét tudja a számtani sor összegének, pl. megkérdezem tőle, ki tudná-e számítani az első 100 szám négyzetének összegét.
Szinte hallom, hogy félbeszakíttok: ,,Ismerjük mi a számtani sor összegének gondolatát is. Nem kell nekünk a képlet. Leírjuk az első száz szám összegét előre is, hátrafelé is.
S=001+92+93+...+98+99+100,S=100+99+98+...+93+92+001;
összeadjuk: 1+100 1+100=101, 2+99=101, 3+98=101, ..., 98+3=101, 99+2=101, 100+1=101, 100-szor lesz  101  tehát
2S=101+101+101+...+101+101+101=100⋅101=10100,
2S=101+101+101+ S=10100:2=5050.''
Ez még mindig nem a számtani sor összegének gondolata, gyerekek, csak az összegképlet levezetése. A gondolat, tudjátok, az a valami, ami a matematikus lelkivilágában felvillanik, amikor rájön, hogy úgy lesz jó az összeget kiszámítani, hogy kétszer is felírjuk, oda-vissza. No lássam, értitek-e ezt a gondolatot? Ki tudná kiszámítani az első 100 szám négyzetének összegét?
Ezt aztán hiába írjátok fel kétféleképpen, oda-vissza:
S=00001+9814+9609+...+9604+9801+10000,S=10000+9801+9604+...+9609+9804+00001,
mert 1+10000=10001, de 4+9801=9805, nem 10001, 9+9604 meg megint más. Aki meg csak a képletre emlékszik, s azt alkalmazza, az rossz eredményt kap.
,,Persze ‐ mondjátok ‐ hiszen ez nem számtani sor.'' Nem is az, mint ahogy a harmadfokú egyenlet sem másodfokú. Mégis, ez a feladat alkalmas annak a megállapítására, megértettétek-e a gondolatot, mert aki megértette, az ettől a nehezebb feladattól sem jön zavarba.
Tudjátok, gyerekek, kétféle rossz diák van. Az egyik azt magolja be, hogy ,,ixegyenlő mínuszbépluszmínusznégyzetgyökbénégyzetmínusznégyácéperkétá'', a másik meg azt, hogy ,,áixnégyzetpluszbéixpluszcé egyenlő nulla, tehát négyánégyzetixnégyzetplusznégyábéixplusznégyácé egyenlő nulla, tehát négyánégyzetixnégyzetplusznégyábéixpluszbénégyzet egyenlő bénégyzetmínusznégyácé, tehát kétáixpluszbé a négyzeten egyenlő bénégyzetmínusznégyácé, tehát ixegyenlő mínuszbépluszmínusznégyzetgyökbénégyzetmínusznégyácéperkétá.'' Lehet, hogy ez az utóbbi egyest kap algebrából, de ez sem jobb, mint a másik. Ez is képletet magolt be, ha logikai képletet is. Ez is csak végeredményt magolt be: annak a gondolkodási folyamatnak a végeredményét, amely a másodfokú egyenlet megoldásának ,,levezetéséhez'' juttatta el azt a matematikust, aki rájött. Nem a képletek, nem is a levezetések érdekesek a matematikában, hanem a gondolatok. Ezeket érdemes megfigyelni, ezek tanítják meg az embert gondolkozni. Ezek nélkül meg üres, unalmas, száraz favágás a matematika.
No hát keressük meg közösen a számtani sor összegezésének gondolatát!
 

II.
 

Azon kezdem, hogy a gondolat benne van a levezetésben, nem fölötte lebeg valahol láthatatlanul; csak azért nehéz ráismerni, mert el van rejtve benne. Talán úgy ismerünk rá legkönnyebben, ha más olyan bizonyítást is keresünk, amiben ugyanaz a gondolat van, csak más köntösbe burkolva. Ami a közös bennük, az a gondolat.
Nos, ki tudna nekem olyan kérdést mondani, amit ugyanezzel a gondolattal oldottunk meg? Hol fordult elő máshol, hogy valamit úgy számoltunk ki, hogy kétszer is vesszük, egyszer egyenesen, egyszer meg fordítva, a kettőt együtt kiszámítjuk, aztán elosztjuk kettővel? Nem arra a gyerekre gondolok, aki állítólag úgy számította ki, hány csirke szaladgál az udvaron, hogy megszámlálta, hány lábuk van, aztán elosztotta kettővel. Az csak tréfa. Meg különben is, hiányzik belőle a lényeges, az, hogy egyszer egyenesen, egyszer meg fordítva. Ugye, már rájöttetek, hogy a háromszög területére gondolok. Azt számítottuk ki úgy, hogy odarajzoljuk fölé, vagy ha tetszik, hogy hasonlóbb legyen a számtani sorhoz, alá, mégegyszer, fordítva. A kettő együtt parallelogrammát ad, annak könnyebb kiszámítani a területét s azt megint elfelezzük, hogy megkapjuk a háromszögét. (Rajzoljátok le! Én nem akarok nagyon sok ábrát rajzolni, mert azt nehezebb kinyomtatni, mint a szöveget.)
No de mi köze a számtani sornak a háromszöghöz? Honnét lehet tudni, hogy a számtani sornál is valami olyasmit kell csinálni, mint a háromszögnél? Hiszen az egyik algebra, a másik meg geometria!
Ez tévedés, gyerekek. Az algebra, meg a geometria nem két tudomány, csak két nyelv, amiken nagyjából ugyanazokat a dolgokat lehet elmondani. Algebrából geometriára éppúgy lehet fordítani, mint franciából magyarra.
A régi görögök még nem nagyon tudtak algebrául, ők sok mindent geometriául mondtak, amit mi algebrául tanulunk. Pl. az (a+b)2=a2+2ab+b2 képletet így mondták: ha egy négyzetnek mind a két oldalát ugyanannyival növeljük meg, területe két olyan téglalap területével növekszik meg, amelyeknek a hosszúsága az eredeti négyzet oldala, szélessége meg annyi, amennyivel megnöveltük a négyzet oldalát, meg még egy olyan négyzet területével, amelynek akkora az oldala, amennyivel az eredeti négyzet oldalát megnöveltük. (1. ábra) Az egyes négyzetekbe és téglalapokba beleírtam a ,,puskát'' is, amelynek segítségével lefordíthatjuk ezt a geometriai tételt algebrai tételre.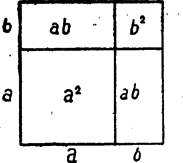
 
 
1. ábra
 

Az első 100 szám összeadásának feladatát biztosan így mondták volna el a régi görögök: van egy négyzet (olyan, mint a kockás füzetben; mondjátok csak nyugodtan kockás füzetnek, én nem haragszom érte); mellette két négyzet (vagy mondjak én is kockát? Jó!) mellette három kocka, mellette négy, s. í. t., egészen, míg 100 kockáig el nem jutunk; hány kocka van összesen?
Száz kockáig nem tudom iderajzolni; hát csak tízig rajzolom (2. ábra). Azon éppúgy látni fogjuk a gondolatot. Nem attól lesz egy matematikai meggondolás általános, hogy n-el írjuk fel; épp olyan jó, ha 10-zel mondjuk el, de úgy, hogy ne használjuk ki, hogy a 10 éppen 10, lehessen helyébe akár 100-at is írni.
 
 
2. ábra
 

Ugye, most már háromszögre hasonlít az ábra? Mégpedig derékszögűre. Szinte kínálkozik, hogy rajzoljuk fölé fordítva. Már oda is rajzoltam, pontozva. Látjátok, téglalap lett belőle. Mindenütt 11 kockányi magas, 10-szer van egymás mellett ilyen 11 kockából álló oszlop, az összesen 110 kocka; a fogazott háromszögben csak feleennyi, 55 kocka volt. Ha 10 helyett 100 kockáig mentem volna, 11 helyett 101 kockából állt volna minden oszlop és 100 ilyen oszlop lenne egymás mellett, az összesen 100⋅101=10100 kocka lenne, a lépcsős háromszögben feleennyi, 5050 kocka. Írjunk ahelyett a 10 helyett, ami akár 100 is lehet, algebrai szokás szerint n-et, ahelyett a 11 helyett meg, ami 101 lesz, ha a 10 nem 10-et, hanem 100-at jelképez, (n+1)-et, akkor megkapjuk a kérdés általános megoldását:
1+2+3+...+(n-1)+n=n(n+1)2.

Látjátok azt is, ugye, hogy nemcsak hasonlít a háromszög területéhez a számtani sor összege, hanem különbözik is tőle valamiben. Abban, hogy a háromszög egy pontban végződik, annak pedig nincs kiterjedése, nem lesz semmivel sem magasabb, ha föléje rajzoljuk megfordítva; ezzel szemben a számtani sor (akarom mondani, a lépcsős háromszög) egy kockával kezdődik, ezért lesz eggyel magasabb, ha fordítva fölérajzoljuk. Ezért lett n+1 kocka a belőle keletkezett téglalap magassága. Még inkább hasonlít hát a lépcsős háromszögünk egy derékszögű trapézre. Annak, ha fordítva fölérajzoljuk, akkora lesz a magassága, mint a trapéz két párhuzamos oldalának összege, alapja meg akkora marad, mint a trapéz két párhuzamos oldalának összege, alapja meg akkora marad, mint a két párhuzamos oldal távolsága, ezért lesz a trapéz területe m(a+b)2. (Nemcsak a derékszögűé; ennek persze az az oka, hogy a ferde parallelogramma területe ugyanakkora, mint a vele közös alapú és magasságú téglalapé.) Ilyen trapézhoz aztán minden számtani sor hasonlít (rajzoljátok meg pl. az 5+8+11+14+... számtani sor első 10 tagjának összegét a kockás füzetben!). Látjátok már, hogy az Sn=n(a1+an)2 és a T=m(a+b)2 képletek édes testvérek? Hát persze, hiszen egy gondolatból születtek.
 

III.
 

Szép, szép, mondjátok, de hogy lesz ebből az első 100 szám négyzetösszege? Ebből sehogy; de hátha sikerül ezt is ügyesen lefordítani geometriára! Rajzoljunk le megint ‐ gondoljátok ‐ 1 kockát, mellé 4 kockát, egymás fölé, melléjük 9 kockát egymás fölé, melléjük 16 kockát, s. í. t., ahogy a négyzetszámok következnek egymás után. Mit kapunk akkor? Ezt a lépcsőt már meg se lehet mászni, egyre magasabbak lesznek a fokai. Nem hasonlít ez sem háromszögre, sem trapézra. Nem is esnek egy egyenesre a lépcsőfokok csúcsai.
Megsúgom, parabolára esnek. Akkor hát valami olyan gondolat kell a négyzetszámok összegezéséhez, mint az olyan háromszög területének kiszámításához, amelynek egyik oldala parabola? Elárulom azt is, hogy épp fordítva, a parabolaszelet területét szokták a négyzetszámok összegezésére visszavezetni.
No de nem csak szóról szóra lehet fordítani! Latinból magyarra is úgy jó fordítani, hogy szép magyar mondatok kerekedjenek ki belőle. Próbáljuk hát most is úgy végezni a fordítást, hogy szép geometriai probléma legyen a négyzetszámok összegezéséből.
Hogy lehet azt? Nagyon egyszerű: igazi, térbeli kockának fordítsuk az 1-et. A 4-et pedig 4 ilyen kockának, négyzetes hasábbá összerakva, hogy ezzel is kifejezzük, azért 4 az összeg második tagja, mert 22. Rakjuk ezeket úgy össze, hogy a kocka alapjának egyik derékszöge a négyzetes hasáb fedőlapjának egyik derékszögére essék. A 9-et 9, négyzetes hasábbá összerakott, kockává fordítsuk le (alapélei 3‐3, magassága 1 kockaélnyi), a 9 előtt levő +-jelet meg úgy fordítsuk le, hogy ezt a négyzetes hasábot hasonlóképpen tegyük a 4 kockából álló négyzetes hasáb alá, ahogy azt tettük az egy kocka alá. És így tovább, amíg 1002 kockáig el nem jutunk. Olyanféle piramist kapunk, mint amilyent a fáraók emeltettek a maguk emlékezetére sok ezer rabszolga szenvedése árán. A 3. ábra ilyen piramist ábrázol, csak kisebbet; 6 jelképezi benne a 100-at. Hány kis kockából áll?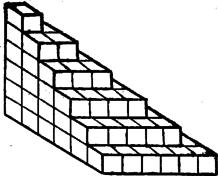
 
 
3. ábra
 

Ahogy a lépcsős háromszög az igazi háromszögre emlékeztet bennünket, a piramisról hasonlóképpen a gúla jut eszünkbe. Valóban, szokás a gúlát is piramisnak hívni, pedig az egyiptomi piramisok inkább a mi kockapiramisunkra hasonlítanak, mint a gúlára. Valami olyan gondolat kellhet hát a négyzetszámok összegezéséhez, mint a gúla köbtartalmának kiszámításához.
De hiszen ez borzasztó, mondjátok. Gúlából hármat kell összerakni, hogy hasáb legyen belőle, méghozzá nem is egybevágót, külön kell bebizonyítani, hogy mégis egyenlő a köbtartalmuk; ráadásul ezt is csak háromoldalú gúlával lehet megcsinálni, a négyoldalút előbb szét kell vágni két háromoldalúra. Talán bizony azzal fogjunk hozzá a piramishoz, hogy szétfűrészeljük négyzetes alapjának átlója mentén? Vagy még csak ne is az átló mentén, hanem valahogyan lépcsőzetesen ?
Ja persze, gyerekek, nem tudjátok, hogy van olyan gúla is, amelynek három példányából könnyebben is lehet hasábot készíteni. S éppen az a gúla ilyen, amelyhez a mi piramisunk hasonlít. Az, amelyiknek négyzet az alapja, az egyik oldaléle merőleges az alapra s éppen olyan magas, mint az alapjának egyik oldala. Három ilyen egybevágó gúlából kocka lesz, ha úgy forgatjuk őket, hogy a csúcsuk essék egybe és a leghosszabb élük. Maradjon például az egyiknek vízszintes az alapja, a másik kettőnek egy-egy egyenlőszárú derékszögű háromszög-oldallapja legyen vízszintes, de felülre kerüljenek. Akkor alapjuk lesz a kocka három egy csúcsba összefutó lapja, a másik három lapja pedig két-két oldallapból lesz. Próbáljátok csak ki, kartonpapírból összeragasztott gúlákkal!
No, most már tudjátok, ugye, azt is, mit csináljatok piramisunkkal, ha meg akarjátok tudni, hány kockából áll. Azt is három példányban kell elkészíteni, s úgy forgatni, hogy négyzetes lapuk közül az egyiké vízszintes legyen, a másiké függőleges, velünk szemben álljon, a harmadiké meg oldalt; s az egykockás csúcsuk találkozzék. No igen, csak az a baj megint, hogy kockában végződnek, nem pontban, mint a gúla. Így aztán nem is kocka lesz belőlük, hanem valami más. Jó térszemlélete legyen annak, aki el tudja képzelni, hogy fér el a három csúcs-kocka egymás mellett s hogy mi lesz az egészből. Melyik mérete növekszik 1-gyel, melyik nem. Azt hiszem, kevesen találtátok ki, mi lesz a három piramisból, ha így összerakjátok; s legtöbbeteknek meglepetést tartogat. Csináljátok meg hát a piramist kartonpapírból három példányban (nem nehéz kisütni, hogy milyen a hálója) és rakjátok össze. Akkor aztán magatok is kitalálhatjátok, mit kell csinálni, hogy, ha nem is kockát, de legalább is hasábot kapjatok belőle.
Rajta hát, csináljátok meg minél előbb és írjátok meg nekem, mennyi az első 100, mennyi az első n szám négyzetének összege?