Cím:	1938. A XLII. Eötvös Loránd matematikai tanulóverseny tételei - 2.
Füzet:	1939/január, 109 - 112. oldal	PDF  |  MathML
Témakör(ök):	Kürschák József (korábban Eötvös Loránd)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Megoldások   a) A XLII. Eötvös Loránd Matemetikai tanulóverseny tételei. 1938. okt. 15   I.   Bebizonyítandó, hogy egy egész szám akkor és csak akkor négyzetösszege két egész számnak, ha kétszerese ily tulajdonságú.   Megoldás. Jelöljön $x$ egy egész számot. Ki kell mutatnunk, hogy ha $x$ két egész szám négyzetösszege, akkor $2x$ is ilyen tulajdonságú; ha pedig $2x$ két egész szám négyzetösszege, akkor $x$ is ilyen tulajdonságú.   $1^0$. Legyen tehát  $x=a^2+b^2$.   Ekkor  $2x=2a^2+2b^2={\left(a+b\right)}^2+{\left(a-b\right)}^2$.   $2^0$. Legyen  $2x=u^2+v^2$.   Kell, hogy $u$ és $v$ egyidőben párosak vagy páratlan számok legyenek; minthogy így $\frac{u+v}{2}$ és $\frac{u-v}{2}$ egész számok, $\begin{array}{c}{\displaystyle x={\left(\frac{u+v}{2}\right)}^2+{\left(\frac{u-v}{2}\right)}^2\mathrm{.}}\end{array}$  Freud Géza (Berzsenyi Dániel g. VII. o. Bp. V.)   Jegyzet. A megoldások egy része nem juttatja kifejezésre a $2^0$. részben, hogy $\frac{u+v}{2}$ és $\frac{u-v}{2}$ egész számok. Egy másik rész pedig csak az $1^0$. részt igazolja.   II.   Bebizonyítandó, hogy minden $1$-nél nagyobb $n$ egész szám $\begin{array}{c}{\displaystyle \frac{1}{n}+\frac{1}{n+1}+\frac{1}{n+2}+\text{...}+\frac{1}{n^2-1}+\frac{1}{n^2}>1.}\end{array}$ I. Megoldás. Ha $n>1$ és a baloldali összegben, $\frac{1}{n+1}$-től kezdve minden nevező helyébe a nála nagyobb $n^2$-t tesszük, akkor mindegyik tört értéke kisebb lesz és így $\begin{array}{c}{\displaystyle f\left(n\right)\equiv \frac{1}{n}+\frac{1}{n+1}+\frac{1}{n+2}+\text{...}+\frac{1}{n^2-1}+\frac{1}{n^2}>\frac{1}{n}+\frac{1}{n^2}+\frac{1}{n^2}+\text{...}+\frac{1}{n^2}\mathrm{.}}\end{array}$ Minthogy az $\frac{1}{n}$-t követő tagok száma $n^2-n$, ${\displaystyle \begin{array}{c}\hfill {\displaystyle f\left(n\right)>\frac{1}{n}+\frac{n^2-n}{n^2}=\frac{1}{n}+1-\frac{1}{n}\mathrm{,}}\hfill \\ \hfill {\displaystyle f\left(n\right)>1.}\hfill \end{array}}$  Gantner Jenő (Szent-István g. VII. o. Bp. XIV.).   II. Megoldás. $f\left(2\right)=\frac{1}{2}+\frac{1}{3}+\frac{1}{4}>1$, mert $\frac{1}{3}>\frac{1}{4}$. ${\displaystyle \begin{array}{cc}\hfill {\displaystyle }& {\displaystyle f\left(3\right)=\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\text{...}+\frac{1}{9}>\frac{1}{3}+\frac{1}{4}+\frac{1}{9}+\frac{1}{9}+\text{...}+\frac{1}{9}}\hfill \\ \hfill {\displaystyle }& {\displaystyle f\left(3\right)>\frac{1}{3}+\frac{1}{4}+\frac{5}{9}>\frac{1}{3}+\frac{1}{4}+\frac{1}{2}}\hfill \end{array}}$ azaz   $f\left(3\right)>f\left(2\right)$.   Kimutatjuk általában, hogy $f\left(n+1\right)>f\left(n\right)$. Ugyanis  $f\left(n\right)=\frac{1}{n}+\frac{1}{n+1}+\frac{1}{n+2}+\text{...}+\frac{1}{n^2}$ ${\displaystyle \begin{array}{c}\hfill {\displaystyle f\left(n+1\right)=\left(\frac{1}{n+1}+\frac{1}{n+2}+\text{...}+\frac{1}{n^2}\right)+\left[\frac{1}{n^2+1}+\text{...}+\frac{1}{{\left(n+1\right)}^2}\right]=}\hfill \\ \hfill {\displaystyle =f\left(n\right)-\frac{1}{n}+\left[\frac{1}{n^2+1}+\text{...}+\frac{1}{{\left(n+1\right)}^2}\right]\mathrm{.}}\hfill \end{array}}$ A szögletes zárójelben foglalt összeget kisebbítjük, ha minden tagjában a legnagyobb nevezőt, ${\left(n+1\right)}^2$-t vesszük; a tagok száma pedig ${\left(n+1\right)}^2-n^2$. Eszerint $\begin{array}{c}{\displaystyle \frac{1}{n^2+1}+\frac{1}{n^2+2}+\text{...}+\frac{1}{{\left(n+1\right)}^2}>\frac{{\left(n+1\right)}^2-n^2}{{\left(n+1\right)}^2}=\frac{2n+1}{{\left(n+1\right)}^2}\mathrm{.}}\end{array}$ Ezen kisebbítéssel azonban még mindig $\frac{1}{n}$-nél többet kapunk, ha $n>1$. T. i. $\begin{array}{c}{\displaystyle \frac{2n+1}{{\left(n+1\right)}^2}>\frac{1}{n}\mathrm{,}\text{ill.}2n^2+n>n^2+2n+\mathrm{1,}\text{mert}n\left(n-1\right)>\mathrm{1,}}\end{array}$ ha $n>1$.Tehát $\begin{array}{c}{\displaystyle f\left(n+1\right)>f\left(n\right)-\frac{1}{n}+\frac{1}{n}\mathrm{,}\text{azaz}f\left(n+1\right)>f\left(n\right)\mathrm{.}}\end{array}$ Kimondhatjuk tehát, hogy $f\left(n\right)$ az $n$-nel monoton növekedő; mivel $f\left(2\right)>1$, egyszersmind $f\left(n\right)>1$.    Taksony György (Ág. ev. g. VIII. o. Bp.)   III. Megoldás. Bontsuk az $f\left(n\right)$ összeg azon részét, mely $\frac{1}{n}$-t követi, részletösszegekre; ezek mindegyikét kisebbítjük, ha mindegyik helyébe a legkisebbiket (utolsót) vesszük. Ezen részletösszegek mindegyikében a tagok száma $n$, Tehát: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle }& {\displaystyle \frac{1}{n+1}+\frac{1}{n+2}+\text{...}+\frac{1}{2n-1}+\frac{1}{2n}>n\frac{1}{2n}=\frac{1}{2}}\hfill \\ \hfill {\displaystyle }& {\displaystyle \frac{1}{2n+1}+\frac{1}{2n+2}+\text{...}+\frac{1}{3n-1}+\frac{1}{3n}>n\frac{1}{3n}=\frac{1}{3}}\hfill \\ \hfill {\displaystyle }& {\displaystyle \frac{1}{3n+1}+\frac{1}{3n+2}+\text{...}+\frac{1}{4n-1}+\frac{1}{4n}>n\frac{1}{4n}=\frac{1}{4}}\hfill \\ \hfill {\displaystyle }& {\displaystyle \cdots \cdots }\hfill \\ \hfill {\displaystyle }& {\displaystyle \frac{1}{\left(n-1\right)n+1}+\frac{1}{\left(n-1\right)n+2}+\text{...}+\frac{1}{n^2-1}+\frac{1}{n^2}>n\frac{1}{n^2}=\frac{1}{n}\mathrm{.}}\hfill \end{array}}$ Eszerint $\begin{array}{c}{\displaystyle f\left(n\right)>\frac{1}{n}+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\text{...}+\frac{1}{n}>n\frac{1}{n}=1.}\end{array}$  Haraszthy András (Szent László g. VI. o. Bp. X.)   III.   Nevezzünk egy háromszög transzverzálisának minden oly egyenesdarabot, mely a háromszög egy csúcsát a szembenfekvő oldalnak (vagy meghosszabbításának) egy pontjával köt össze. Bebizonyítandó, hogy minden hegyesszögű háromszöghöz létezik a térnek oly pontja, ahonnan a háromszög valamennyi transzverzálisa derékszög alatt látszik.   Megoldás. Az $ABC△$ $A$ csúcsából kiinduló $A{A}_i$ transzverzális derékszög alatt látszik a transzverzális, mint átmérő fölé írt gömbfelület minden pontjából (és csakis ezekből). Ezen gömb keresztülmegy az $A$ ponton és az $A$ pontból húzott magasság $A\text{'}$ talppontján, mert $AA\text{'}{A}_i\sphericalangle ={90}^{\circ }$. A gömb középpontja az $AA\text{'}$ magasságot merőlegesen felező egyenesen fekszik. Ebből következik, hogy valamennyi ilyen gömb átmegy az $AA\text{'}$, mint átmérő fölött, a háromszög síkjára merőleges ${\Sigma }_1$ síkban rajzolt körön. 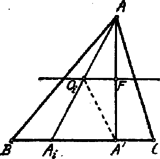    Ha ezen kör egy pontja $P$, az $A{A}_i$-hez tartozó gömb középpontja $O_i$, és $AA\text{'}$ magasság felező pontja, a szóbanforgó kör középpontja $F$, akkor $O_{i}FP△\cong O_{i}FA△\left(\cong O_{i}FA\text{'}△\right)$. T. i. $O_{i}F=O_{i}F$, $FP-FA\left(=FA\text{'}\right)$ és $OF\perp {\Sigma }_1$, azaz $O_{i}FP\sphericalangle =O_{i}FA\sphericalangle \left(=O_{i}FA\text{'}\sphericalangle \right)={90}^{\circ }$. Ebből következik, hogy $O_{i}P=O_{i}A\left(=O_{i}A\text{'}\right)$, tehát a ${\Sigma }_1$ síkban fekvő kör minden pontja az $O_i$ középpont körül $O_{i}A\left(=\frac{1}{2}A{A}_i\right)$ sugárral leírt gömb felületen fekszik. Eszerint az $AA\text{'}$ magasság, mint átmérő fölött a ${\Sigma }_1$ síkban leírt $k_a$ kör bármely pontjából bármely $A{A}_i$ transzverzális derékszög alatt látszik. Hasonlóan a $B{B}_j$ transzverzálisok a $BB\text{'}$ magasság, mint átmérő fölött, az $ABC△$ síkjára merőleges ${\Sigma }_2$ síkban leírt $k_b$ kör, a $C{C}_l$ transzverzálisok a $CC\text{'}$ magasság, mint átmérő fölött, az $ABC△$ síkjára merőleges ${\Sigma }_3$ síkban leírt $k_c$ kör pontjaiból látszanak derékszög alatt. Ha az $ABC△$ hegyesszögű, akkor a háromszög $H$ magassági pontja a háromszögön belül fekszik. Kimutatjuk, hogy ebben az esetben a $k_a$, $k_b$, $k_c$ körök az $ABC$ sík fölött (vagy alatt) egy $S$ pontban metszik egymást. 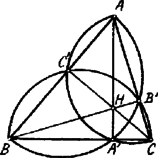    A $H$ pontban az $ABC△$ síkjára emelt $HZ$ merőleges a ${\Sigma }_1$, ${\Sigma }_2$, ${\Sigma }_3$ síkok közös egyenese. $HZ$ egyenes a $k_a$, $k_b$, $k_c$ kört messe rendre a $P_a$, $P_b$, $P_c$ pontban. Minthogy $A{P}_{a}A\text{'}$, $B{P}_{b}B\text{'}$, $C{P}_{c}C\text{'}$ háromszögek a $P_a$, $P_b$, $P_c$ csúcsoknál derékszögűek és ezekben $H{P}_a$, $H{P}_b$, $H{P}_c$ az átfogóhoz tartozó magasságok, $\begin{array}{c}{\displaystyle {\overline{HP}}_a^2=\overline{AH}\cdot \overline{HA\text{'}}\mathrm{,}{\overline{HP}}_b^2=\overline{BH}\cdot \overline{HB\text{'}}\mathrm{,}{\overline{HP}}_c^2=\overline{CH}\cdot \overline{HC\text{'}}}\end{array}$ Azonban az $ABC△$ síkjában az $AB$, $BC$, $CA$ oldalak, mint átmérők fölött írt körök párjainak hatványvonalai a magasságok és így a magassági pont hatványa mindegyik körére nézve ugyanakkora, azaz $\begin{array}{c}{\displaystyle AH\cdot HA\text{'}=\overline{BH}\cdot \overline{HB\text{'}}=\overline{CH}\cdot \overline{HC\text{'}}}\end{array}$ és így $\begin{array}{c}{\displaystyle H{P}_a=H{P}_b=H{P}_c\mathrm{,}\text{ill.}{P}_a\equiv P_b\equiv P_c\equiv S\mathrm{.}}\end{array}$ Ebből az $S$ pontból az $ABC△$ bármely transzverzálisa derékszög alatt látszik. 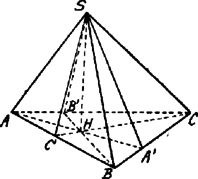    Ha a háromszög derékszögű, pl. $A$-nál, akkor a $k_a$, $k_b$, $k_c$ körök az $A$ pontban érintik egymást. Az $A$ csúcsból a $B{B}_j$ és $C{C}_l$ transzverzálisok derékszög alatt látszanak, míg az $A{A}_i$ transzverzálisok $0^0$-ú szög alatt. Ha $ABC△$ tompaszögű, pl. $A$-nál, akkor a $k_a$ kör az $ABC△$-et belül hasítja, a $k_b$ és $k_c$ körök a háromszögön kívül hasítják a háromszög síkját, tehát közös pontjuk nem lehet.    Volena-Koczor Imre (Révai Miklós g. VII. o. Győr).