Kezdőlap


Cím:	A parabola néhány metrikus tulajdonságáról
Szerző(k):	Dr. Kárteszi Ferenc
Füzet:	1939/május, 197 - 202. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A koordinátarendszer alkalmas választása esetén $y = x^{2}$ a parabola egyenlete. Ez esetben $(t, t^{2})$ pontok ‐ röviden $t$ pontok ‐ képezik a parabolát.
A parabola $| t_{1} t_{2} |$ -húrjának irányhatározója: $(t_{1}^{2} - t_{2}^{2}) : (t_{1} - t_{2}) = t_{1} + t_{2}$ és így az egyenlete:

\begin{matrix} y - t_{1}^{2} = (t_{1} + t_{2}) (x - t_{1}) . \end{matrix}

Ezen az alapon bármely

t

parabolapontban tüstént felírható az érintő és a normális egyenlete is:

\begin{matrix} y - t^{2} = 2 t (x - t) \end{matrix}

ill.

\begin{matrix} y - t^{2} = - \frac{1}{2 t} (x - t) . \end{matrix}

Vagy ha a

t

paraméter hatványai szerint rendezzük a két egyenletet:

\begin{matrix} t^{2} - 2 x t + y = 0 ... \end{matrix}

(1)

ill.

\begin{matrix} t^{3} + \frac{1 - 2 y}{2} t - \frac{x}{2} = 0 ... \end{matrix}

(2)

Röviden csak

t

érintőről, ill.

t

normálisról beszélünk.

I. Egy pontból a parabolához két érintőt húzhatunk.
Adva van az

(x_{0}, y_{0})

, keresendő belőle a parabolához sugárzó érintő

t

paramétere! Az 1. szerint

\begin{matrix} t^{2} - 2 x_{0} t + y_{0} = 0. \end{matrix}

Keresendő tehát e

t

-ben másodfokú egyenlet két gyöke:

t_{1}, t_{2}

. Ez a két gyök két érintőt jelent (valós gyökök esetén):

\begin{matrix} t_{i}^{2} - 2 x_{0} t_{i} + y_{0} = 0 ahol i = 1, 2. \end{matrix}

A gyökök és együtthatók ismert összefüggése alapján

\begin{matrix} t_{1} + t_{2} = 2 x_{0} & s innen & x_{0} = \frac{t_{1} + t_{2}}{2} \\ t_{1} t_{2} = y_{0} & ezért & y_{0} = {(t_{1}^{2} \cdot t_{2}^{2})}^{\frac{1}{2}} . \end{matrix}

Eszerint

x_{0}

az érintési pontok abscissainak számtani, az

y_{0}

pedig az ordináták mértani középarányosa. ¹ Az

(x_{0}, y_{0})

pontot

| t_{1} t_{2} |

húr pólusának nevezzük.

II. Egy pontból három normális húzható a parabolához.
Az előbbi mintára megkeressük az adott

(x_{0}, y_{0})

pontból kisugárzó normális

t

paraméterét. Ez a

\begin{matrix} t^{3} + \frac{1 - 2 y_{0}}{2} t - \frac{x_{0}}{2} = 0 \end{matrix}

harmadfokú egyenlet gyöke. Az egyenlet harmadfokú, tehát három gyöke van,

t_{1}, t_{2}, t_{3}

és mindegyikhez tartozik egy normális ²:

\begin{matrix} t_{i}^{3} + \frac{1 - 2 y_{0}}{2} t_{i} - \frac{x_{0}}{2} = 0 ahol i = 1, 2, 3. \end{matrix}

Az egyenletből hiányzik a

t^{2}

-es tag. Ezért s a gyökök és együtthatók ismert összefüggése alapján:

\begin{matrix} t_{1} + t_{2} + t_{3} = 0, t_{1} t_{2} + t_{2} t_{3} + t_{3} t_{1} = \frac{1 - 2 y_{0}}{2}, t_{1} t_{2} t_{3} = \frac{x_{0}}{2} . \end{matrix}

Írhatjuk ezeket a következő alakban is

\begin{matrix} t_{1} + t_{2} + t_{3} = 0 ... & (3) \\ {\begin{matrix} x_{0} = 2 t_{1} t_{2} t_{3} \\ y_{0} = \frac{1 - 2 (t_{1} t_{2} + t_{2} t_{3} + t_{3} t_{1})}{2} \end{matrix}} ... & (4) \end{matrix}

Megfordítva: ha felvesszük a 3. egyenletnek eleget tevő három pontot a parabolán, akkor azok normálisai a 4. egyenlet segítségével szerkesztett

(x_{0}, y_{0})

pontban találkoznak.

III. A parabola görbületi köre, sugara és középpontja.
Legyen

t_{1}

a parabolának egyik szilárd pontja. Messük el e ponthoz tartozó normálist a tetszőleges

t_{2}

normálisával. A metszéspont határhelyzet felé tart az első normálison, mialatt

t_{2}

t_{1}

felé tart. Származtatása folytán e metszéspont határhelyzetéből, mint középpontból

t_{1} = t_{2}

ponton átvezetett kör két végtelenül közelfekvő pontban érinti a parabolát. E kör középpontjából a fentiek szerint ‐ még egy

t_{3}

normális sugárzik a parabolához. Feltételünkből

(t_{1} = t_{2})

és a 3. alapján

t_{3} = - 2 t_{1}

, tehát elhagyhatók az indexek s a szilárd

t_{1}

pont paraméterét szerepeltetjük index nélkül. Így 4. alapján a szóbanforgó kör középpontjának a koordinátái:

\begin{matrix} {\begin{matrix} x = - 4 t^{3} \\ y = \frac{1 + 6 t^{2}}{2} ... \end{matrix} \end{matrix}

(5)

Ezt a kört a parabola

t

pontjához tartozó görbületi körnek, középpontját ill. sugarát görbületi középpontnak ill. görbületi sugárnak, a sugár reciprok értékét görbületnek nevezzük.
A kör általános helyzetben

{(x - a)}^{2} + {(y - b)}^{2} - ϱ^{2} = 0

egyenletnek felel meg. Ez alapon a görbületi kör egyenlete:

\begin{matrix} {(x + 4 t^{3})}^{2} + {(y - \frac{1 + 6 t^{2}}{2})}^{2} - ϱ^{2} = 0 \end{matrix}

s mivel átmegy e kör a

(t, t^{2})

ponton:

\begin{matrix} {(t + 4 t^{3})}^{2} + {(t^{2} + \frac{1 + 6 t^{2}}{2})}^{2} - ϱ^{2} = 0. \end{matrix}

Innen rövid számítással mind a görbületi sugár, mind a köregyenlet kiadódik:

\begin{matrix} ϱ^{2} = 16 t^{6} + 12 t^{4} + 3 t^{2} + \frac{1}{2} ... & (6) \\ x^{2} + y^{2} + 8 t^{3} x - (1 + 6 t^{2}) y - 3 t^{4} = 0 & (7) \end{matrix}

IV. A parabola evolutája.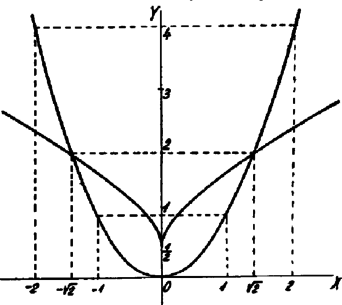

Minthogy a parabola minden pontjához más és más görbületi-kör tartozik, felmerül a kérdés: mi a középpontjuknak a mértani helye? A görbületi középpontok mértani helyét a parabola evolutájának nevezzük. Paraméteres egyenletrendszerét már ismerjük is: az 5. egyenletrendszer az, ha a

t

változó. Fejezzük ki belőle

t

parameter harmadik, illetőleg második hatványát. Ezután

t^{3}

-ét négyzetre,

t^{2}

-ét köbre emeljük s ezáltal a

t

paraméter kiküszöbölhető. Ily módon megkapjuk a parabola evolutájának egyenletét:

\begin{matrix} \frac{27}{2} x^{2} = {(2 y - 1)}^{3} ... \end{matrix}

(8)

Definiálhattuk volna az evolutát úgy is, mint a parabola normálisai által burkolt görbét. Ezt a továbbiak folyamán be fogjuk igazolni. Kimutatjuk ugyanis, hogy a 8. egyenlettel jellemzett görbe érintői azonosak a parabola normálisaival.

a) A parabola evolutája harmadrendű görbe. ³
Hány pontban metszi az általános helyzetű ⁴

\begin{matrix} u x + v y + 1 = 0 \end{matrix}

egyenes az evolutát, vagyis hány görbületi középpont van az egyenesen? Evégből az 5. egyenlet értékeit helyettesítjük egyenesünk egyenletébe és ezt még

t

hatványai szerint rendezzük:

\begin{matrix} t^{3} - \frac{6 v}{8 u} t^{2} - \frac{2 + v}{8 u} = 0 ... \end{matrix}

(9)

Az egyenlet

t

-ben harmadfokú, tehát három gyöke van:

t_{1}, t_{2}, t_{3}

. Tekintve, hogy az egyenlet elsőfokú tagja hiányzik, a gyökök és együtthatók összefüggése alapján:

\begin{matrix} t_{1} + t_{2} + t_{3} = \frac{6 v}{8 u}, t_{1} t_{2} + t_{2} t_{3} + t_{3} t_{1} = 0, t_{1} t_{2} t_{3} = \frac{2 + v}{8 u} . \end{matrix}

Ezeket még a következő alakban is írhatjuk:

\begin{matrix} t_{1} t_{2} + t_{2} t_{3} + t_{3} t_{1} = 0 ... & (10) \\ {\begin{matrix} u = \frac{3}{12 t_{1} t_{2} t_{3} - 2 (t_{1} + t_{2} + t_{3})} \\ v = \frac{4 (t_{1} + t_{2} + t_{3})}{12 t_{1} t_{2} t_{3} - 2 (t_{1} + t_{2} + t_{3})} \end{matrix} & (11) \end{matrix}

Megfordítva: ha felveszünk a parabolán a 10. egyenletet kielégítő három pontot, akkor a 11. egyenlettel meghatározott

u x + v y + 1 = 0

egyenes tartalmazza a három ponthoz tartozó görbületi középpontot.
Bármely

t

paraméterhez egy evoluta pontot rendel az 5. képlet, tehát röviden csak az evoluta

t

pontja kifejezést használjuk. Láttuk, hogy az evolutát tetszőleges egyenes három pontban metszi és e metszéspontok paraméterei között 10. fejezi ki a determináló kapcsolatot.

b) A parabola evolutája harmadosztályú görbe.
Az evoluta két végtelenül közelfekvő

t_{1} = t_{2}

pontját összekötő egyenes az evoluta érintője; az előbbiek szerint még egy

t_{3}

pontban metszi az evolutát. A tizedik egyenlet szerint és a

t_{1} = t_{2}

feltétel folytán:

t_{3} = - \frac{t_{1}}{2}

. Tehát az indexezés fölösleges és így a 11. alapján írható

\begin{matrix} u = - \frac{1}{2 t^{3} + t}, v = - \frac{2 t}{2 t^{3} + t} \end{matrix}

együtthatók értelmezik az érintő egyenest. Innen az egyenlete

\begin{matrix} - x - 2 t y + (2 t^{3} + t) = 0, \end{matrix}

vagy még

\begin{matrix} t^{3} + \frac{1 - 2 y}{2} t - \frac{x}{2} = 0 ... \end{matrix}

(2')

alakban is írható. Az evoluta

t

pontjához tartozó érintő, (röviden csak

t

érintő) azonos tehát a parabola

t

normálisával ‐ amint már előre is jeleztük. Ezen az alapon mondhatjuk, hogy egy pontból három érintő húzható az evolutához, amelyeknek paramétereit a 3. egyenlet rendeli egymás mellé.

V. A parabola és görbületi köreinek közös húrjai egy újabb parabola érintői.
A parabolának görbületi-köreivel képezett metszéspontjait úgy határozzuk meg, hogy ez utóbbi egyenletébe (7.)

x = τ, y = τ^{2}

paramétereket helyettesítjük; ez által a

\begin{matrix} τ^{4} - 6 t^{2} τ^{2} + 8 t^{3} τ - 3 t^{4} = 0 ... \end{matrix}

(12)

τ

-ban negyedfokú egyenletre jutunk. Látható azonban, hogy a baloldal négy tényezőre bontható:

\begin{matrix} {(τ - t)}^{3} (τ + 3 t) = τ^{4} - 6 t^{2} τ^{2} + 8 t^{3} τ - 3 t^{4} ... \end{matrix}

(13)

Ez azt jelenti, hogy

t

a 12. egyenletnek háromszoros,

- 3 t

pedig egyszeres gyöke. Tehát a

t

ponthoz tartozó görbületi kör három végtelenül közel fekvő pontban (

t

-ben) metszi a parabolát és egy ezeken kívüli (

- 3 t

) negyedik pontban is. E szerint a görbületi- és simuló-kör azonos fogalmak. ⁵
Írjuk fel most a

t

és

- 3 t

pontokat összekötő húr egyenletét:

\begin{matrix} y - t^{2} = (- 3 t + t) (x - t) = - 2 t (x - t) . \end{matrix}

Ezután vegyük szemügyre az

x^{2} = - 3 y

parabola érintőjét az

(x_{1}, y_{1})

pontban, az

\begin{matrix} y - y_{1} = - \frac{2}{3} x_{1} (x - x_{1}) \end{matrix}

egyenest. Ezt az új parabolát az

x_{1} = 3 t, y_{1} = - 3 t^{2}

kielégíti és ebben a pontban

y + 3 t^{2} = - 2 t (x - 3 t)

az érintője. Azonban rögtön látható, hogy ez azonos az

y - t^{2} = - 2 t (x - t)

húrral. Tehát

y = x^{2}

parabolának görbületi köreivel képezett közös húrjai az

y = - \frac{1}{3} x^{2}

parabolát burkolják.

VI. A parabola bármely talpponti-háromszögének súlypontja a parabola tengelyén van.
Fentebb már megmutattuk, hogy egy tetszőleges

(x_{0}, y_{0})

pontból az evolutához húzott érintők, vagyis a vezérlő parabola normálisai különös ‐ a 3. egyenletet kielégítő ‐ három pontot indukálnak a parabolán. Ezeket a pontokat a normálisok talppontjainak szokás nevezni és így e három pont képezte háromszöget a parabola valamely talpponti-háromszögének,

(x_{0}, y_{0})

pontot e háromszög generátorának nevezzük.
A talpponti háromszög súlypontjának rendezői:

\begin{matrix} \frac{t_{1} + t_{2} + t_{3}}{3}, \frac{t_{1}^{2} + t_{2}^{2} + t_{3}^{2}}{3}; \end{matrix}

ezek közül a 3. egyenlet miatt az elsőnek az értéke

= 0

. Ez azt jelenti, hogy a talpponti-háromszög súlypontja az

Y

tengelyen van.
Évfolyamunk 1. számában kimutattuk, hogy a talpponti-háromszögnek

y = x^{3}

parabolára való (

Y

tengellyel párhuzamos) vetülete egy egyenesbe eső három pont. Ugyancsak az ott tárgyaltakból látható: a talpponti-háromszög köré írt kör átmegy a parabola csúcspontján is. ⁶

VII. A parabola simulóponti-háromoldalának súlypontja a csúcsérintőn van.
Amint mondottuk már, görbületi- vagy simuló-kör aequivalens fogalmak. Tetszőleges

(u, v)

egyenes három pontban metszi az evolutát, miáltal három ‐ a 10. egyenletnek eleget tevő ‐ pontot indukál a parabolán. E három pont három coaxiális simuló kör simuló pontja, azért e három ponthoz tartozó parabola érintők képezte három oldalt a parabola simulóponti-háromoldalának nevezzük. E háromoldal csúcsainak koordinátái az I.-részben mondottak szerint:

\begin{matrix} (\frac{t_{1} + t_{2}}{2}, t_{1} t_{2}), (\frac{t_{2} + t_{3}}{2}, t_{2} t_{3}), (\frac{t_{3} + t_{1}}{2}, t_{3} t_{1}) \end{matrix}

alakban írhatók. Ez alapon a háromoldal súlypontjának koordinátái:

\begin{matrix} \frac{t_{1} + t_{2} + t_{3}}{3}, \frac{t_{1} t_{2} + t_{2} t_{3} + t_{3} t_{1}}{3} . \end{matrix}

Ezek közül a második

= 0

(a 10. egyenlet folytán), tehát a súlypont csakugyan az

Y

koordináta tengelyen van.

VIII. Keressük meg az

y^{2} = x^{3}

görbének és a

y = m x + b

általános helyzetű egyenesnek a metszéspontjait. A görbe nem más, mint a

(t^{2}, t^{3})

pontok összessége. Keressük meg tehát a

\begin{matrix} t^{3} - m t^{2} - b = 0 \end{matrix}

harmadfokú egyenlet gyökeit. A három

(t_{1}, t_{2}, t_{3})

gyökre most is fennállanak a

\begin{matrix} t_{1} t_{2} + t_{2} t_{3} + t_{3} t_{1} = 0 \\ m = t_{1} + t_{2} + t_{3} \\ b = t_{1} t_{2} t_{3} \end{matrix}

összefüggések. Ezeket a 10. és 11. egyenletekkel vessük össze. Kimondhatjuk, hogy az

u x + v y + 1 = 0

egyenes által indukált simulóponti-háromoldal csúcsainak ‐

Y

-tengellyel párhuzamos ‐ vetületei az

y^{2} = x^{3}

görbén egy

y = m x + b

egyenesbe esnek, ahol

\begin{matrix} m = \frac{6 v}{8 u}, b = \frac{2 + v}{8 u} . \end{matrix}

Befejezésül három szép tétel bebizonyítását tűzöm ki az olvasónak.
I. Valamely talpponti háromszög oldalaira polárháromszögének megfelelő csúcsaiból bocsájtott merőlegesek egy pontban találkoznak. E pont és a háromszög generátor pontja közé eső távolságot a t. p. h. köré írt kör középpontja felezi.
II. Talpponti háromszög csúcsaihoz tartozó simuló körök még egy talpponti háromszöget metszenek ki a parabolából. Simulóponti háromoldal simuló pontjaihoz tartozó simuló körök még egy s. p. h. o. simulópontjait metszik ki a parabolából.
III. A parabola tetszőlegesen adott érintőjét három simuló-kör érinti még, amelyeknek simuló érintője az adottal egy újabb kör köré írt négyszög.
(Ez a tétel Laguerre-től ered.)

Győrött, 1938. nov. 2. Dr. Kárteszi Ferenc
áll. gimn. tanár

¹V. ö. az 1446. feladattal. (Ezen évfolyam 3 számában, ‐ 1938/11 70. old .)

²Valós gyököket tételezünk fel. L. IV. évfolyamunkban a 285. feladatot.

³Harmadrendű egy görbe, ha tetszőleges egyenes három pontban metszi. Harmadosztályú, ha egy pontból három érintő sugárzik hozzá.

⁴ $A x + B y + C = 0$ egyenesnél $u = \frac{A}{C}, v = \frac{B}{C}$ .

⁵V. ö. XI. évf. 9‐10 sz. Dr. Kárteszi: Az ellipszis.

⁶V.ö. XV. évf. 1. sz. 13‐14. old. L. még a 262. feladatot IV. évf. 1. számában.