Kezdőlap


Cím:	Megjegyzések a tanulóverseny II. feladatához
Szerző(k):	Faragó Andor
Füzet:	1938/január, 132 - 134. oldal	PDF \| MathML
Témakör(ök):	OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

a) Egyik-másik megoldásban felmerült azon állítás, hogy az érintkező $k_{1}$ és $k_{2}$ körök köré írt gömb $ω$ középpontja a két kör síkjának szögét felező síkban fekszik. Két sík szögét felező sík bármely pontja a két kör síkjától egyenlő távolságban van, azaz eszerint $O_{1} ω = O_{2} ω$ lenne, ami nyilván csakis azon esetben lehet igaz, ha az $O_{1}$ és $O_{2}$ körök sugarai egyenlők.
Az előbbi ‐ téves ‐ felfogás szerint $ω$ oly gömb középpontja is lenne, mely a $P$ $(A B C)$ triéder lapjait (belülről) érinti. Általában azonban csakis azon gömb középpontja, mely a triéder éleit az $A$ , $B$ , $C$ pontokban érinti.
Ugyanis, amint a megoldásban láttuk, az $ω$ gömb keresztülmegy az $A$ , $B$ , $C$ pontokon. Láttuk továbbá, hogy az $A P$ egyenes merőleges $Σ_{3}$ síkra, tehát $A P ⊥ ω A$ ; ez annyit jelent, hogy $A P$ az $ω$ gömböt az $A$ pontban érinti. Hasonlóan $B P ⊥ ω B$ és $C P ⊥ ω C$ : a $P$ $(A B C)$ triéder élei az $ω$ gömböt az $A$ , $B$ , $C$ pontban érintik.
Mivel pedig $ω A = ω B = ω C$ és $P A = P B = P C$ ,^{$^{*}$} a $P ω$ egyenes merőleges az $A B C$ síkra és ezt az $A B C △$ köré írt kör középpontjában döfi. Azt is mondhatjuk, hogy az $ω$ gömb oly kúpfelületet érint az $A B C △$ köré írt kör mentén, melynek tengelye $P$ -ből az $A B C △$ síkjára állított merőleges és a $P (A B C)$ triéder élei alkotói. Ha $P$ a végtelenbe kerül, akkor a kúpból henger lesz, melyet az $ω$ gömb az $A B C △$ köré írt kör mentén érint: ezen kör az $ω$ gömb legnagyobb köre lesz.
b) III. évfolyamunkban (119. o.) a 200. feladatban a következő kérdéssel foglalkoztunk: mi a feltétele annak, hagy két kör a térben ugyanazon gömbön feküdjék.^{$^{*}$}
Legyen a két kör $(O_{1})$ és $(O_{2})$ ; síkjuk metszésvonala $R S$ . Ha $(O_{2})$ -t $R S$ körül az $(O_{1})$ síkjában forgatjuk, kapjuk az $(O'_{2})$ kört. Hogy $(O_{1})$ és $(O_{2})$ ugyanazon gömbön feküdjék, annak szükséges és elégséges feltétele, hogy $R S$ az $(O_{1})$ és $(O'_{2})$ körök hatványvonala legyen.
Ezen feltétel kielégítése ugyanis magában foglalja azon követelmény kielégítését, hogy ha a két kör síkjára az $O_{1}$ ill. $O_{2}$ középpontban merőlegeseket emelünk, ezek (egy síkban feküdve) valóban messék egymást, mégpedig egy olyan $ω$ pontban, mely az $(O_{1})$ és $(O_{2})$ körök minden pontjától egyenlő távolságban van.
Ha az $(O_{1})$ és $(O_{2})$ körök valóban egy gömbön feküsznek, melynek középpontja $ω$ , akkor $ω O_{1} ⊥ (O_{1})$ és $ω O_{2} ⊥ (O_{2})$ , tehát az $O_{1} ω O_{2}$ sík merőleges az $(O_{1})$ és $(O_{2})$ síkok mindegyikére és így e két sík $R S$ metszővonala merőleges az $O_{1} ω O_{2}$ síkra. Ha ezen síkot $R S$ az $M$ pontban metszi, $R S ⊥ M O_{1}$ , és $R S ⊥ M O_{2}$ . Forgassuk az $O_{2}$ síkját az $O_{1}$ síkjába: akkor ezen forgásnál $M O_{2}$ állandóan merőleges marad $R S$ -re és így az $[O_{1}]$ síkban $M O_{1}$ egyenessel esik össze, azaz $R S$ merőleges a két kör centrálisára, $O_{1} O_{2}$ -re. Azonban $M$ pontnak úgy az $(O_{1})$ , mint az $(O_{2})$ körre vonatkozó hatványa megegyezik az $M$ pontnak az $ω$ gömbre vonatkozó halványával: kell, hogy $R S$ az $O_{1}$ és $O'_{2}$ körök hatványvonala legyen. Ezen feltétel tehát szükséges!
Megfordítva: ha az $[O_{1}]$ és $[O_{2}]$ metszővonala, $R S$ , hatványvonala az $(O_{1})$ és $(O'_{2})$ köröknek úgy, hogy e két kör centrálisa $R S$ -t az $M$ pontban metszi, akkor $O_{1} M ⊥ R S$ és $O_{2} M ⊥ R S$ , tehát az $O_{1} M O_{2}$ sík is $⊥ R S$ . Az $O_{1} M O_{2}$ síkban állítsunk $O_{1}$ -ben $O_{1} M$ -re, $O_{2}$ -ben $O_{2} M$ -re merőlegest: ezen két merőleges metszőpontja legyen $ω$ . Ekkor $ω O_{1} ⊥ [O_{1}]$ , mert merőleges az $[O_{1}]$ sík két egyenesére, t. i. $O_{1} M$ -re és $R S$ -re. Hasonlóan $ω O_{2} ⊥ [O_{2}]$ . Ebből következik: hogy $ω$ az $(O_{1})$ , ill. $(O_{2})$ minden pontjától egyenlő távolságban van. Most még csak azt kell kimutatnunk, hogy $ω$ távolsága az $(O_{1})$ pontjaitól megegyezik az $(O_{2})$ pontjaitól való távolságával.

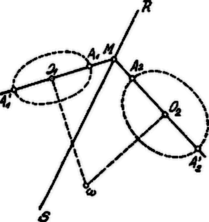
Feltettük azonban, hogy

R S

(O_{1})

és

(O'_{2})

körök hatványvonala. Ha

M O_{1}

(O_{1})

kört az

A_{1}

és

A'_{1}

M O_{2}

(O_{2})

kört az

A_{2}

és

A'_{2}

(diametrálisan szembenfekvő) pontokban metszi, akkor

\begin{matrix} \bar{M A_{1}} \cdot \bar{M A'_{1}} = \bar{M A_{2}} \cdot \bar{M A_{2}'}, \end{matrix}

azaz az

A_{1}

A'_{1}

A_{2}

A_{2}'

pontok egy körön feküsznek, melynek középpontja nyilván

ω

, tehát

\begin{matrix} ω A_{1} = ω A'_{1} = ω A_{2} = ω A'_{2} = R, \end{matrix}

ahol

R

a gömb sugara, és az

A

pontokon átmenő kör a gömb egyik legnagyobb köre.
c) Már most felvethetjük a kérdést: mi a feltétele annak, hogy három, különböző síkban fekvő kör egy gömbön feküdjék? A három kör síkjai egy triéder lapjai. A triéder élei

e_{1}

e_{2}

e_{3}

. Ezeknek a b) alatti feltételt kell kielégíteniük, azaz

e_{1}

hatványvonala legyen a

k_{2}

és

k'_{3}

^{$^{*}$}
(vagy

k_{3}

és

k'_{2}

) körök.
Ha

e_{1}

hatványvonala a

k_{2}

és

k'_{3}

köröknek,

k_{2}

és

k_{3}

egy gömbön feküsznek, melynek középpontja

ω

, az

O_{2}

-ben a

k_{2}

síkjára és az

O_{3}

-ban a

k_{2}

síkjára állított

f_{2}

és

f_{3}

merőlegesek metszőpontja. Azonban

e_{2}

hatványvonala a

k_{3}

és

k'_{1}

köröknek;

k_{3}

és

k_{1}

oly gömbön feküsznek, melynek középpontja közös pontja az

O_{1}

-ben a

k_{1}

síkjára állított

f_{1}

merőlegesnek és

f_{3}

-nak. Továbbá

e_{3}

k_{1}

és

k'_{2}

körök hatványvonala:

k_{1}

és

k_{2}

oly gömbön feküsznek, mely az

f_{1}

és

f_{2}

metszőpontja. Eszerint a nem egy síkban fekvő

f_{1}

f_{2}

és

f_{3}

egyenesek páronként metszik egymást, kell tehát, hogy

f_{1}

f_{2}

és

f_{3}

egyenesek egy ponton menjenek keresztül és ezen pont

ω

, a szóbanforgó gömb középpontja.

(Forgassuk a

k_{2}

-t

e_{3}

körül

k_{1}

síkjába,

k'_{2}

helyzetébe, a

k_{3}

-t

e_{2}

körül ugyancsak

k_{1}

síkjába

k'_{3}

helyzetébe. Ekkor

e_{3} ⊥ O_{1} O'_{2}

és

e_{2} ⊥ O_{1} O'_{3}

. Ezen forgatásoknál az

e_{1}

az első esetben

e'_{1}

, a második esetben

e''_{1}

helyzetbe kerül.

O'_{2}

-ből az

e'_{1}

-re ill. az

O'_{3}

-ből az

e''_{1}

-re állított merőleges talppontja

M'_{1}

ill.

M''_{1}

; ezekre nézve

P M'_{1} = P M''_{1}

. Az

e'_{1}

pontjainak

k'_{2}

körre vonatkozó hatványa megegyezik az

e''_{1}

megfelelő pontjainak a

k'_{3}

körre vonatkozó hatványával. A

P

pontnak mind a három körre vonatkozó hatványa egyenlő: a

P

pontból egyenlő hosszúságú érintődarabokat húzhatunk a három körhöz.)
A II. versenytételben megadott helyzet ezen általánosabb helyzetnek különös esete. Ha ugyanis a három kör páronként érintkezik, akkor két-két kör közös érintője ‐ t. i. a két kör síkjának metszésvonala ‐ a két körnek hatványvonala lesz, ha az egyik kör síkját ezen vonal körül ‐ a másik kör síkjába forgatjuk.

^{$^{*}$}

ω A P △ =_{}^{\infty} ω B P △ =_{}^{\infty} ω C P △

, mert

ω A = ω B = ω C = R

ω P

közös és

ω P

-vel szemben fekvő szög derékszög.

^{$^{*}$}A körök síkjai nem párhuzamosak!

^{$^{*}$} $\begin{matrix} Ha & k_{3}-t & e_{1} & körül & k_{2} & síkjába & forgatjuk, & keletkezik & k'_{2}, \\ Ha & k_{2}-t & e_{1} & ,, & k_{3} & ,, & ,, & ,, & k'_{2}.-nek s. í. t. \end{matrix}$