Kezdőlap


Cím:	A tetraéderről 2. (1938. március)
Szerző(k):	Dr. Egerváry Jenő
Füzet:	1938/március, 193 - 196. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Előző közleményünkben (l. ezen évf. 2. számában) a tetraédernek a köréírt gömbbel kapcsolatos tulajdonságait tárgyaltuk; a következőkben a tetraédernek éleit, illetve lapjait érintő gömbre vonatkozó néhány jellegzetes tételt fogunk ismertetni.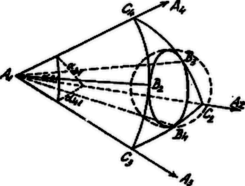
Először a lapokat érintő, azaz beírt ¹ gömbbel foglalkozunk. A tetraéder belső lapszögeit felező hat síknak mindig van közös pontja és ezen közös pont mindegyik tetraéderlaptól egyenlő távolságra van, tehát beírt gömb mindig létezik.
A beírt gömb egyik jellemző tulajdonsága a következő: Kössük össze a tetraéder egyik háromszöglapjának csúcsait a beírt gömbnek rajtalevő érintési pontjával; az összekötő egyenesek (transzverzálisok) ² által alkotott szögek legyenek $σ'$ , $σ''$ , $σ'''$ . Akkor a többi lapokon is, az érintési pont körül hasonló módon ugyanakkora $σ'$ , $σ''$ , $σ'''$ szögek keletkeznek. (Bang tétele.) A $σ'$ , $σ''$ , $σ'''$ szögek egyenlők a tetraéder-élekből alakakítható torznégyszögek fél szögösszegével.

Jelöljük az

A_{1} A_{2} A_{3} A_{4}

tetraéderbe írt gömb érintéspontjait

B_{1}

B_{2}

B_{3}

B_{4}

-gyel, továbbá az

i

-dik lapban a

k

-ik csúcsnál fekvő élszöget

α_{i k}

-val (általában

α_{i k} \neq α_{i k}

) és tekintsük először a tetraéder egyik, például

A_{1}

csúcsnál lévő triéderét. Az

A_{1}

csúcsból az

\bar{A_{1} A_{2}}

\bar{A_{1} A_{3}}

\bar{A_{1} A_{4}}

élek és az

\bar{A_{1} B_{2}}

\bar{A_{1} B_{3}}

\bar{A_{1} B_{4}}

transzverzálisok indulnak ki. Szerkesszünk

A_{1}

köré gömböt, mely a tőle egyelő távolságra lévő ³

B_{2}

B_{3}

B_{4}

érintéspontokon átmegy. Ez a gömb a triédert egy gömbháromszögben, a tetraéderbe írt gömböt pedig körben metszi, mely kör nyilván az előbbi gömbháromszög oldalait érinti, tehát

\begin{matrix} \hat{B_{3} A_{1} A_{2}} & = \hat{B_{4} A_{1} A_{2}}^{4} & \hat{B_{2} A_{1} A_{3}} + \hat{B_{2} A_{1} A_{4}} = α_{21} \\ egyrészt \hat{B_{4} A_{1} A_{3}} & = \hat{B_{2} A_{1} A_{3}} másrészt & \hat{B_{3} A_{1} A_{4}} + \hat{B_{3} A_{1} A_{2}} = α_{31} \\ \hat{B_{2} A_{1} A_{4}} & = \hat{B_{3} A_{1} A_{4}} & \hat{B_{4} A_{1} A_{2}} + \hat{B_{4} A_{1} A_{3}} = α_{41} \end{matrix}

⁴ következésképpen

\begin{matrix} \hat{B_{3} A_{1} A_{2}} & = \hat{B_{4} A_{1} A_{2}} = \frac{\hat{A_{2} A_{1} A_{3}} + \hat{A_{2} A_{1} A_{4}} - \hat{A_{3} A_{1} A_{4}}}{2} = \frac{α_{31} + α_{41} - α_{21}}{2} \\ \hat{B_{4} A_{1} A_{3}} & = \hat{B_{2} A_{1} A_{3}} = \frac{\hat{A_{3} A_{1} A_{4}} + \hat{A_{3} A_{1} A_{2}} - \hat{A_{4} A_{1} A_{2}}}{2} = \frac{α_{41} + α_{21} - α_{31}}{2} & (1) \\ \hat{B_{2} A_{1} A_{4}} & = \hat{B_{3} A_{1} A_{4}} = \frac{\hat{A_{4} A_{1} A_{2}} + \hat{A_{4} A_{1} A_{3}} - \hat{A_{2} A_{1} A_{3}}}{2} = \frac{α_{21} + α_{31} - α_{41}}{2} . \end{matrix}

Ugyanilyen összefüggések állapíthatók meg a többi csúcsok körüli élszögekre, ill. ezek részeire is.
Ezen összefüggések alapján közvetlenül kitejezhetjük a

B_{i}

érintéspontokból húzott transzverzálisok által bezárt szögeket a tetraéder élszögei segélyével:

\begin{matrix} \hat{A_{1} B_{4} A_{2}} = \hat{A_{1} B_{3} A_{2}} = 180^{\circ} - (\hat{B_{3} A_{1} A_{2}} + \hat{B_{3} A_{2} A_{1}}) = \\ = 180^{\circ} - \frac{α_{31} + α_{32} + α_{41} + α_{42} - α_{21} - α_{12}}{2} = \frac{α_{34} + α_{43} + α_{21} + α_{12}}{2} \end{matrix}

eszerint

\begin{matrix} \hat{A_{3} B_{2} A_{4}} & = \hat{A_{3} B_{1} A_{4}} = \hat{A_{1} B_{4} A_{2}} = \hat{A_{1} B_{3} A_{2}} = \frac{α_{34} + α_{43} + α_{12} + α_{21}}{2} = σ' \\ \hat{A_{2} B_{3} A_{4}} & = \hat{A_{2} B_{1} A_{4}} = \hat{A_{1} B_{2} A_{3}} = \hat{A_{1} B_{4} A_{3}} = \frac{α_{24} + α_{42} + α_{13} + α_{31}}{2} = σ'' & (2) \\ \hat{A_{1} B_{2} A_{4}} & = \hat{A_{1} B_{3} A_{4}} = \hat{A_{2} B_{1} A_{3}} = \hat{A_{2} B_{4} A_{3}} = \frac{α_{14} + α_{41} + α_{23} + α_{32}}{2} = σ''' \end{matrix}

azaz: a tetraéder

\bar{A_{i} A_{k}}

és

\bar{A_{l} A_{m}}

szemközti élei a (szomszédos) érintéspontokból

\begin{matrix} \frac{α_{i k} + α_{k i} + α_{l m} + α_{m l}}{2} \end{matrix}

szög alatt látszanak. Az így nyert eredménynek nyilvánvaló következménye a említett Bang-féle tétel: A tetraéderlapokon levő

B_{i}

érintéspontokból a csúcsokhoz húzott transzverzálisok mind a négy lapon ugyanazon

σ'

σ''

σ'''

szögeket alkotják.
A

σ'

σ''

σ'''

szögek (2) alapján a következőképpen is jellemezhetők: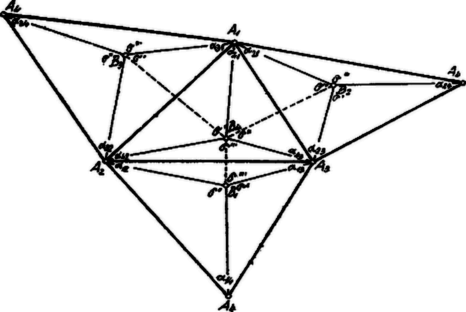

Ha a tetraéder éleiből minden lehető módon elhagyunk egy-egy szemközti élpárt, úgy három torznégyszöget nyerünk. A

σ'

σ''

σ'''

szögek ezen torznégyszögek fél szögösszegeivel egyenlők. A fenti eredményt ezek szerint a háromszög-geometriából ismeretes szög-koordináták felhasználásával még a következőként fogalmazhatjuk: ⁵
A beírt gömb érintéspontjainak a szögkoordinátái mind a négy tetraéderlapon ugyanazok, éspedig egyenlők a tetraéderélekből alkotható három torznégyszög fél szögösszegével.
Izogónikusnak nevezzük az olyan tetraédert, melynek összes élei a beírt gömb (szomszédos) érintéspontjaiból a

120^{\circ}

alatt látszanak. A fentiek szerint egy tetraéder nyilván akkor és csak akkor izogónikus, ha az élekből alkotható három torznégyszög mindegyikének szögösszege

240^{\circ}

. ⁶

Ha egy triéder élszögeit felezzük és a felező egyeneseken át a megfelelő triéderlapokra merőleges síkokat állítunk, akkor ez a három felező merőleges sík egymást egy egyenesben metszi. ⁷ Az így nyert egyenes a triéder köré írt körkúp tengelye, vagyis azon pontok mértani helye, melyek a három triéderéltől egyenlő távolságra vannak.
Ha egy tetraéder mindegyik triéderéhez megszerkesztjük a körülírt körkúpot, a négy kúp tengelyei általában nem találkoznak egy pontban, tehát általában nincs olyan pont, mely egy tetraéder összes éleitől egyenlő távolságra van, nincs tehát olyan gömb sem, mely a tetraéder összes éleit érinti. Ilyen ,,élérintő'' gömb létezésekor a tetraéder alkatrészei közt bizonyos feltételek állnak fenn, melyek mint látni fogjuk, teljesen analógok a kör köré írt négyszög alkatrészei közt fennálló feltételekhez.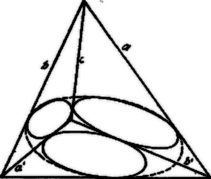

Ha ugyanis a tetraéder

a

b

c

a'

b'

c'

élei (l. ábra) egy gömböt érintenek, úgy nyilván azon három torznégyszög oldalai közt, melyek két-két szemközti él elhagyásával keletkeznek, ugyanazon feltételeknek kell fennállaniok, mint egy kör köré írt négyszög oldalai közt, azaz

\begin{matrix} a + a' = b + b' = c + c' \end{matrix}

(3)

Ki fogjuk mutatni, hogy ezen szükséges feltételek egyúttal elegendők is, azaz: Egy tetraédernek akkor és csak akkor van (belső) élérintő gömbje, ha a szembenlevő élek hosszúságösszegei egyenlők.

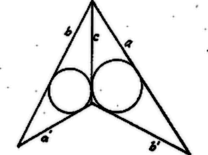Szerkesszünk mindegyik tetraéderlapba érintő kört. Az

(a b' c)

, illetve

(a' b c)

lapba írt kör érintéspontjainak az

(a b c)

csúcstól való távolsága

\begin{matrix} \frac{a + c - b'}{2}, ill. \frac{b + c - a'}{2}, \end{matrix}

ezen távolságok azonban a (3) relációk alapján egyenlők, tehát az

(a' b' c)

és

(a' b c)

lapokba írt körök érintik egymást. Miután az előbbi meggondolás mindegyik lappárra érvényes, tehát következik, hogy a tetraéderlapokba írt körök a (3) feltételek fennállása esetén egymást páronként érintik és pedig úgy, hogy az összes érintéspontok különbözők. Ekkor pedig a négy tetraéderlapba írt kör (l. ezen évf. 5. számában az 1364. feladatot) egy gömbön fekszik és az így meghatározott gömb a tetraéder élérintő gömbje. Az így nyert eredményt még a következőképpen fogalmazhatjuk: A belső élérintőgömb létezésének szükséges és elegendő feltétele az, hogy a tetraéderlapokba írt körök egymást páronként érintsék.
Hasonlóképen kimutatható, hogy egy tetraédernek akkor és csak akkor van külső élérintő gömbje (azaz olyan, mely egyes éleknek a meghosszabbításait érinti) ha a tetraéder élek közt a

\begin{matrix} a - a' = b - b' = c - c' \end{matrix}

feltételek állnak fenn.

Egerváry Jenő

¹Tehát azzal a gömbbel, mely a tetraéderlapokat egy-egy belső pontban érinti. Tudvalevőleg hét olyan érintő gömb létezik, mely egyes tetraéderlapok meghosszabbításait érinti.

²,,Transzverzális'' rendesen a háromszög csúcsát a szembenfekvő oldal valamely pontjával összekötő távolságot jelenti. Itt ezen kifejezést tágabb értelemben, a rövidebb fogalmazás kedvéért használjuk az egyes tetraédercsúcsokat a szomszédos érintési pontokkal összekötő távolságokra is.

³Ha a gömbhöz egy kívülfekvő pontból tetszőleges számú érintőt húzunk, az érintéspontok az érintők közös pontjától egyenlő távolságra vannak.

⁴A $B_{2} B_{3} B_{4}$ gömbi kör a $C_{2} C_{3} C_{4}$ gömbháromszögbe írt érintő kör. A $C_{i}$ csúcs egyenlő gömbi távolságban van a $B_{k}$ , $B_{l}$ érintési pontoktól. Tehát pl. $\hat{C_{3} B_{4}} = \hat{C_{3} B_{2}}$ és így, $\hat{B_{4} A_{1} A_{3}}$ és $\hat{B_{2} A_{1} A_{3}}$ mint kongruens körívekhez tartozó középponti szögek egyenlők.
Egyszersmind utalunk arra, hogy az (1) alatti formulák ugyanolyan szerkezetűek, mint amelyek a síkháromszögbe írt kör érintési pontjának a szomszédos csúcsoktól való távolságát fejezik ki.

⁵A háromszög geometriában a sík valamely pontjának a háromszöghöz viszonyított szögkoordinátái: a pontot a háromszög csúcsaival összekötő transzverzálisok által alkotott szögek. A háromszög belső pontjaira nézve ezen szögkoordináták összege nyilván $360^{\circ}$ .

⁶Az $n$ oldalú torzsokszög szögeinek összege kisebb, mint az $n$ oldalú konvex síksokszög szögeinek összege! (L. III. évf. 85. o. 187. feladatban.)

⁷A bizonyítás azon alapul, hogy ha egy szög felezőjén át a szög síkjára merőleges síkot fektetünk, akkor ezen sík bármely pontja a szög vagy csúcsszögének száraitól egyenlő távolságban van.