Kezdőlap


Cím:	A tetraéderről 1. (1937. október)
Szerző(k):	Dr. Egerváry Jenő
Füzet:	1937/október, 33 - 37. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A tetraéder a legegyszerűbb síklapú test, melyet négy háromszöglap határol. Ámbár ugyanaz a szerepe a térmértanban, mint a háromszögnek a síkmértanban, általános tulajdonságai és osztályozása nem oly közismertek, mint a háromszögnél. Ennek oka nem csupán az, hogy a tetraéder több és többféle alkatrésszel bír mint a háromszög és így bonyolultabb alakzat, hanem az is, hogy a tetraédernek ‐ mint általában minden testnek ‐ az ábrázolása szemléletesség szempontjából tökéletlen, különösen akkor, ha a tetraéder bizonyos kitüntetett fajait ábrázoljuk.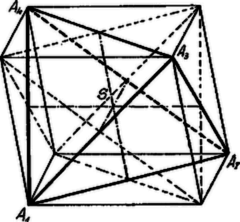
Ilyen kitüntetett fajok az egyenlőlapú és a magasságponttal bíró tetraéder. Mindkettő figyelemreméltó módon mutatja, hogy a tetraéder és a háromszög között nem teljes az analógia.
Egyenlőoldalú háromszög csak egyféle van, t. i. a szabályos háromszög, melynek összes alkatrészei (oldalai, szögei) egyenlők. Ezzel szemben egyenlőlapú tetraéder számtalan sokféle van, a lapok területeinek egyenlősége nem vonja maga után az alkatrészek (élek, élszögek, lapszögek) egyenlőségét.
Másrészt viszont közismert, hogy bármely háromszög magasságai egy pontban találkoznak. Ezzel szemben a tetraéder magasságai általában nem metszik egymást, még páronként sem.

Jelen sorokban a tetraédernek néhány általános tulajdonságát, elsősorban pedig a most említett fajait fogjuk ismertetni. Ezen ismertetésnél hasznos segédeszköznek fog bizonyulni a körülírt parallelepipedon, amely nem csupán a tárgyalásnak fog bizonyos szemléletességet adni, hanem a tetraéder-alkatrészek közti összefüggések levezetését is jelentékenyen megkönnyíti.

Fektessünk a tetraéder minden egyes élén át a szembenfekvő éllel párhuzamos síkot. Az így nyert hat sík közül kettő-kettő nyilván párhuzamos, tehát parallelepipedont alkotnak. A parallelepipedon bármely lapjának átlói a tetraédernek két szembenfekvő élével egyenlők és párhuzamosak. A tetraéder két szemközti élének felezőpontjait összekötő távolságokat nevezzük Klug Lipót nyomán röviden éltengelynek. Egy éltengely nyilván a parallelepipedon szembenfekvő lapjainak középpontjait köti össze, tehát az éltengelyek a körülírt parallelepipedon megfelelő éleivel egyenlők és párhuzamosak és egymást egy pontban, a közös felező pontjukban metszik.¹ Ezen pont egyszersmind a tetraéder súlypontja.
Ki fogjuk mutatni, hogy a fent említett tetraéderfajok a körülírt parallelepipedon segélyével a következő módon jellemezhetők.
I. Egy tetraéder akkor és csak akkor egyenlőlapú, ha a körülírt parallelepipedon derékszögű.
II. Egy tetraédernek akkor és csak akkor van magasságpontja, ha a körülírt parallelepipedon egyenlő élű.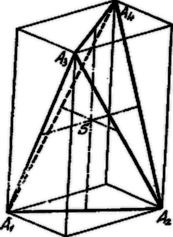

I. Ha az

A_{1} A_{2} A_{3} A_{4}

tetraédernek pl. az

A_{1} A_{2} A_{3}

és

A_{1} A_{2} A_{4}

lapjai egyenlő területűek, úgy az

A_{3}

és

A_{4}

csúcsok az

\bar{A_{1} A_{2}}

éltől egyenlő távol vannak, tehát az

\bar{A_{1} A_{2}}

és

\bar{A_{3} A_{4}}

élek normális transzverzálisa az

\bar{A_{3} A_{4}}

élt felezi². Ha a tetraéder egyenlő lapú, azaz mind a négy lap ugyanakkora területű, úgy az előbbi meggondolásból következik, hogy mindegyik szemben levő élpár normális transzverzálisa felezi az éleket. Más szóval az éltengelyek egybeesnek a normális transzverzálisokkal, a körülírt parallelepipedonnak az éltengelyekkel párhuzamos élei merőlegesek a szemközti tetraéder élekkel párhuzamos parallelepipedonlapokra, azaz a körülírt parallelepipedon derékszögű.
Minthogy pedig a derékszögű parallelepipedont határoló téglalapok átlói egyenlők, tehát az egyenlőlapú tetraéder szemben levő élei egyenlők és ennek következtében a lapjai egybevágók.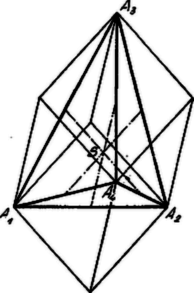

II. Ha az

A_{1} A_{2} A_{3} A_{4}

tetraédernek, pl. az

\bar{A_{1} H_{1}}

és

\bar{A_{2} H_{2}}

magasságai metszik egymást egy

H

pontban, úgy

\begin{matrix} \bar{A_{1} H_{1}} ⊥ A_{2} A_{3} A_{4} és \bar{A_{2} H_{2}} ⊥ A_{1} A_{3} A_{4} . \end{matrix}

Tehát az

\bar{A_{3} A_{4}}

él merőleges a két magasságot tartalmazó

A_{1} A_{2} H

síkra, kővetkezésképp az abban fekvő

\bar{A_{1} A_{2}}

élre is. Ha mind a négy magasság a

H

pontban találkozik, úgy az előbbi meggondolásból következik, hogy a szemben levő élpárok egymásra merőlegesek. E szerint a körülirt parallelepipedon lapátlói, melyek a tetraéder szembenfekvő élpárjaival párhuzamosak, szintén merőlegesek egymásra, tehát a lapok rombusok, azaz a körülirt parallelepipedon egyenlőélű.
A tétel megfordítását, miszerint ez egyenlőélű parallelepipedonba írt tetraéder magasságai egy pontban találkoznak, a következő, a tetraéderrel kapcsolatos gömböket tárgyaló fejezetben fogjuk közvetlenül bizonyítani.
A következőkben egymással szembeállítjuk az egyenlőlapú és a magasságponttal bíró tetraéderek nevezetesebb tulajdonságait a kettő közt fennálló reciprocitás kihangsúlyozása céljából.

\begin{matrix} Az egyenlőlapú tetraédernél a körül- & A magasságponttal bíró tetraédernél a \\ írt parallelepipedon derékszögű tehát: & körülírt parallelepipedon egyenlőélű, tehát: \\ az éltengelyek egymásra merőlegesek; & az éltengelyek egyenlő hosszúak, \\ az éltengelyek merőlegesek a szemben- & a szembenfevő élpárok négyzetösszegei \\ fekvő élpárokra, & egyenlők egymással és az éltengely négy- \\ a szembenfevő élek egyenlő hosszúak, & zetének négyszeresével, \\ a magasságok egyenlő hosszúak. & a szembenfekvő élek egymásra merőlegesek. \end{matrix}

Tudvalevőleg minden háromszöghöz tartozik egy beírt és egy körülírt kör, hasonlóképp minden tetraédernek van körülírt és beirt gömbje. Egyenlőlapú tetraédernél az éltengelyek metszéspontja (azaz a súlypont), egyenlő távolságban van a körülírt derékszögű parallelepipedon valamennyi csúcsától: ezek között vannak a tetraéder csúcsai is. Tehát a tetraéder súlypontja egyszersmind a körülírt gömb középpontja. Minthogy pedig a magasságok egyenlők, a súlypont egyenlő távolságban van a tetraéder lapjaitól és így a beírt gömbnek is középpontja.
A háromszög Feuerbach-féle körének azonban csak a magassági ponttal bíró tetraédernél van analogonja.
³
Fentebb kimutattuk, hogy a magasságponttal bíró tetraéder éltengelyei egyenlők. Ha tehát ezek közös felezési pontja körül, közös hosszuk felével, mint sugárral, gömböt szerkesztünk, ez a gömb átmegy mind a hat él felezőpontján, tehát tartalmazza a tetraéderlapok Feuerbach-féle köreit és így természetesen a lapmagasságok talppontjait is.
A tetraéderhez tartozó további gömbök tárgyalása céljából először levezetjük a következő tételt:
Egyenlőélű parallelepipedonba írt tetraéder magasságai egy pontban találkoznak és ez a magasságpont a körülírt gömb középpontjának a súlypontra vonatkozó tükörképe.
Jelöljük az egyenlő élű parallelepipedonnak a beírt tetraéderhez tartozó csúcsait

A_{1}, A_{2}, A_{3}, A_{4}

, a többit

B_{1}, B_{2}, B_{3}, B_{4}

-gyel. Ekkor a tetraéderhez nem tartozó bármelyik, pl. a

B_{1}

csúcsból a megfelelő

A_{2} A_{3} A_{4}

lapra bocsátott merőleges

U_{1}

talppontja a három egybevágó

B_{1} U_{1} A_{2}

B_{1} U_{1} A_{3}

B_{1} U_{1} A_{4}

derékszögű háromszöget határozza meg, úgy hogy

U_{1} A_{2} = U_{1} A_{3} = U_{1} A_{4}

, tehát a

B_{i}

csúcsokból a megfelelő tetraéderlapra bocsátott merőlegesek a tetraéderlapok köré írt körök

U_{i}

középpontjain mennek át, vagyis egymást a körülírt gömb

U

középpontjában metszik. Ennélfogva a

B_{i}

pontokkal az

S

súlypontra vonatkozólag szimmetrikusan fekvő

A_{i}

tetraéder csúcsokból a megfelelő tetraéderlapokra bocsátott merőlegesek: a magasságok, szintén egy

H

pontban találkoznak. A beirt tetraédernek tehát van magasságpontja és ez a

H

magasságpont nyilván

U

-nak

S

-re vonatkozó tükörképe.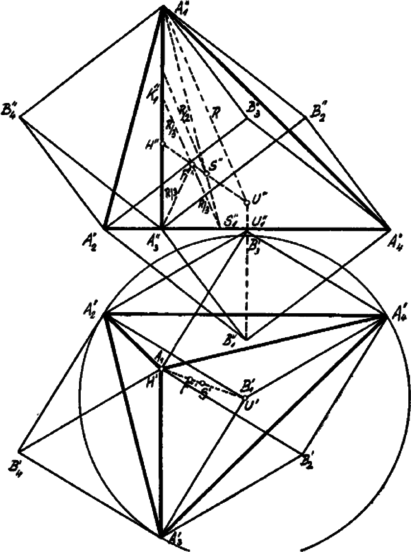

Ebből az ábra szerint azonnal következik, hogy

S

körül

R / 2

sugárral leírt gömb a felső magasságmetszetek középpontjain megy át. Itt

R

a tetraéder köré írt gömb sugarát jelenti.
Ha a tetraéder mindegyik csúcsába egy, a magasságpontba két tömegegységet helyezünk, az így nyert tömegrendszer súlypontja a

H S

távolság azon

F

pontja, melyre

\bar{S F} : \bar{F H} = 2 : 4

.
Ha továbbá a fenti tömegekből a két egyenlő tömegű

(A_{1}) + (H) + (H)

és

(A_{2}) + (A_{3}) + (A_{4})

csoportot alkotjuk, úgy

(A_{2}) + (A_{3}) + (A_{4})

súlypontja az

A_{2} A_{3} A_{4}

tetraéderlap

S_{1}

súlypontja,

(A_{1}) + (H) + (H)

súlypontja a

\bar{A_{1} H}

felső magasságmetszet egyharmadában levő

K_{1}

pont,⁴ a közös

F

súlypont felezi az

S_{1} K_{1}

távolságot tehát

S_{1}

,-től és

K_{1}

-tól, valamint nyilván a

S_{1} K_{1} H_{1}

derékszögű háromszög

H_{1}

csúcsától is

R / 3

távolságra van,⁵ azaz:
A magasságponttal bíró tetraédernél a súlypont és magasságpont közti távolságot

1 : 2

arányban osztó

F

pont körül

R / 3

sugárral leírt gömb átmegy a lapok súlypontjain, a magassági talppontokon és a felső magasságmetszetek harmadában levő osztáspontokon.
Budapest, 1937.

Egerváry Jenő

¹L. folyóiratunk II. évf. 101., 130., 161. o. (Kárteszi F.: A tetraéderről.) (Lásd 1925/12. 101. old, 1926/1. 130. old., 1926/2. 161. old. ‐A szerk.

²Ha az $e$ egyenes a vele nem párhuzamos $f$ egyenesnek $A$ és $B$ pontjaitól egyenlő távolságra van, úgy az $e$ és $f$ normális transzverzálisa az $A B$ távolságot felezi.

³Az éltengely két szembenfekvő él felezési pontjait, azaz az egyenlőélű parallelepipedon két párhuzamos lapjának középpontjait köti össze. Ezért az éltengely a parallelepipedon élével, vagyis egy rombus oldalával egyenlő, míg a szembenfekvő élek ezen rombus átlóival egyenlők. (L. a 393. feladatot, V. évf. 54. o. ‐ 1928/10. 54.old.)

⁴ $H K_{1} = \frac{1}{3} H A_{1}$ .

⁵Ugyanis $H F = \frac{2}{3} H S = \frac{2}{3} \cdot \frac{1}{2} H U = \frac{1}{3} H U$ és $H K_{1} = \frac{1}{3} H A_{1}$ ; tehát $F K_{1} = \frac{1}{3} U A_{1} = \frac{1}{3} R$ .