|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Folyóiratunk XIII. évfolyamának 8. számában a ,,Sokszögekre vonatkozó szélsőérték feladatokról'' című közlemény bizonyos ‐ zárt konvex görbékkel kapcsolatos ‐ szélsőérték tulajdonságú sokszögekkel foglalkozik.
Bebizonyítja, hogy:
1. A zárt konvex görbébe írható maximális területű -szögre fennáll, hogy a görbéhez bármelyik csúcspontjában húzott érintő párhuzamos a két szomszédos csúcsponton átfektetett szelővel.
2. A zárt konvex görbe körül írható minimális területű -szög bármely oldalát az érintési pont felezi.
3. A zárt konvex görbét területileg legjobban megközelítő -szög minden oldalát saját felezőpontja és a görbével való két metszéspontja négy egyenlő részre osztja.
Ezen háromféle extrém sokszöget azonban a fenti egy-egy tulajdonságuk nem határozza meg, azaz a fenti feltételek tetszésszerinti zárt konvex görbe esetén szükségesek, de nem elégségesek. Azonban kör esetében elégségesek is.
A következőkben bebizonyítjuk, hogy ezen szükséges feltételek ellipszis esetén is elégségesek.
A) Meghatározandó az ellipszisbe írható legnagyobb területű -szög.
Először megrajzoljuk a főkört és megszerkesztjük a főkörbe írható szabályos -szöget. Ezen -szög affin megfelelője lesz az ellipszisbe írható legnagyobb területű szög. (Az affinitásról részletesen I. XI. évfolyamunk 241. o.) Ilyen szög azonban végtelen sok van. Ugyanis a körbe írt szabályos -szög elforgatható és minden helyzetében megszerkeszthetjük az affin megfelelőjét.
a) Ezen -szögek és csakis ezek mindegyike tesz eleget az 1. szükséges feltételnek. Ugyanis a körbe írt szabályos sokszög egyik csúcsában húzott érintő, az egyenes párhuzamos a szomszédos csúcsokat összekötő egyenessel (1. ábra); tehát és , az affin megfelelőjük is párhozamosak.
b) Ezen -szögek területe egyenlő és nagyobb területű -szög nem írható az ellipszisbe.
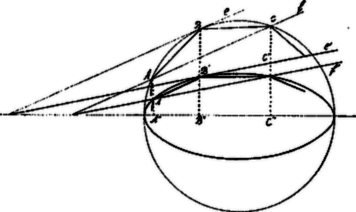 1. ábra
Bontsunk ugyanis fel egy ilyen -szöget trapézekre az 1. ábrán látható módon.(A körbe írható szabályos -szög csúcspontjaiból bocsássunk merőlegest a nagy tengelyre). Akkor bármely két megfelelő trapéz területének viszonya, pl.: | |
ahol az ellipszis fél nagy tengelyét, a fél kis tengelyét jelenti.
Ezért a trapézek összegére, azaz az és -szögre is fennáll, hogy:
ahol a körbe írt -szög, pedig ez ellipszisbe írható megfelelő -szög területét jelenti. Mivel és állandók, tehát: szintén állandó.
Nagyobb területű -szög nem írható az ellipszisbe, mert különben az I. alapján a körbe is lehetne a szabályos -szögnél nagyobb területű n szöget írni, már pedig a körbe írható -szögek közül a szabályos -szög területe a legnagyobb.
Az 1. szükséges feltétel ellipszis esetén tehát elégséges is.
B) Meghatározandó az ellipszis köré írható legkisebb területű -szög.
Az ellipszis köré írható legkisebb területű szög a főkör köré írt szabályos -szög affin megfelelője.
a) Csakis ezekre nézve áll fenn, hogy az érintési pont az oldalakat felezi. Ugyanis kör esetén ilyen tulajdonsággal csak a köré írható szabályos -szög rendelkezik. Tehát csak ennek affin megfelelője rendelkezik szintén ilyen tulajdonsággal. (L. a 2. ábrán).
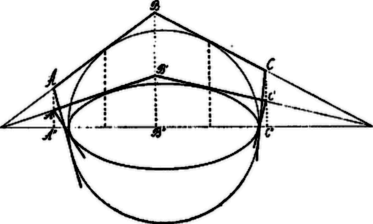 2. ábra
b) Ilyen -szög, a kör köré írható szabályos szög helyzete szerint, az ellipszisnél is végtelen sok van. Ezek területe azonban egyenlő és ezeknél kisebb területű -szög nem írható az ellipszis köré. Ugyanis az előbbi esetben analóg módon látható, hogy: ahol és most az ellipszis, illetve a kör köré írható -szögek területét jelenti. Mivel a jobboldal állandó, a baloldal is az. Ha az ellipszis köré lehetne ezeknél kisebb területű -szöget is írni, akkor a kör köré is lehetne. Kör esetén azonban a 2. tulajdonságuk csak a köré írható szabályos szögeknek van meg. Ezekből következik, hogy a 2. feltétel ellipszis esetén is elégséges.
C) Az ellipszist területileg legjobban approximáló -szög.
Most is először a főkört területileg legjobban approximáló -szöget szerkesztjük meg. Ez úgy történik, hogy előbb megszerkesztjük a körbe írható szabályos -szöget és ennek minden oldalát négy egyenlő részre osztjuk. Azután a két szélső osztó pontot projiciáljuk a kör középpontjából a körre. (3. ábra.) Az így nyert pontokat összekötjük. A keletkezett -szög lesz a keresett extrém tulajdonságú -szög körre nézve.
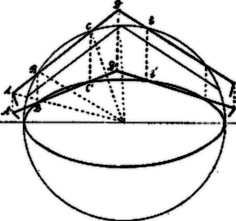 3. ábra
Ennek affin megfelelője lesz az ellipszist területileg legjobban approximáló sokszög.
Ilyen szög szintén végtelen sok van, azonban:
a) Ezek mindegyike eleget tesz a 3. feltételnek.
b) Az ellipszist területileg egyenlően approximálják. Ugyanis a kör és az sokszög oldalai által határolt terület úgy aránylik az ellipszis kerülete és a megfelelő sokszög által határolt területhez, mint .
Tehát ha az ellipszisnek lenne ezen -szögeknél területileg jobban approximáló -szöge, akkor a körnek is lenne a fenti módon szerkesztett -szögnél jobban approximáló -szöge, ez azonban feltevésünkkel ellenkezik. Tehát a 3. feltétel ellipszis esetén is elégséges.
Budapest
Adler Ernő
gyakorlóiskolai tanárjelölt
Olyan -szög, amely a körre nézve a 3) feltételt kielégíti, csak egy van és ez a leírt módon szerkesztett -szög. Szerkesszünk ugyanis egy olyan oldalt, amely a 3. feltételnek megfelel; legyen ez pl. (3. ábra). A végpontból húzzunk szelőket; ezek között a -n kívül még csak egynek lesz meg az a tulajdonsága, ami -nak megvan (t. i. a -nek) és ezen szelő szeleteinek hossza megegyezik a szeleteivel. Hogy az így keletkező szabályos -szög területileg valóban legjobban közelíti meg a körét, annak bizonyításával itt nem foglalkozunk. |
 PDF | MathML
PDF | MathML