Kezdőlap


Cím:	A XII. évfolyam 9-10. számában kitűzött pályatételek megoldása
Szerző(k):	Csizmás L. , Harsányi János , Komlós János , Nagy Elemér
Füzet:	1937/február, 161 - 166. oldal	PDF \| MathML
Témakör(ök):	Egyéb (KöMaL pontverseny is)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Található-e olyan

c

szám, amely mellett az

\begin{matrix} x^{3} - 6 x^{2} - 271 x + c = 0 \end{matrix}

egyenletnek mindegyik gyöke (valós és) egész szám?
Telkes

Megoldás. A számítás egyszerűsítése végett alakítsuk át az egyenletet

y^{3} + p y + q = 0

alakra. Legyen

x = y + a

. Ekkor

\begin{matrix} {(y + a)}^{3} - 6 {(y + a)}^{2} - 271 (y + a) + c = 0, \end{matrix}

és

y

hatványai szerint rendezve

\begin{matrix} y^{3} (3 a - 6) y^{2} + ({3 a}^{2} - 12 a - 271) y + (a^{3} - 6 a^{2} - 271 a + c) = 0. \end{matrix}

y^{2}

együtthatója zérus, ha

3 a - 6 = 0

, vagyis ha

a = 2

. Ekkor az egyenlet alakja

\begin{matrix} y^{3} - 283 y + (c - 558) = 0 ... \end{matrix}

(1)

Vizsgáljuk, hogy az (1) egyenletnek

c

mely értékénél van három valós egész számú gyöke? (Ez esetben lesz az eredeti egyenletnek is).

Írjuk fel az egyenletet

\begin{matrix} y (b^{2} - 283) = - (c - 558) ... \end{matrix}

(2)

alakban. Innen minden egész számú

y

érték mellett kapunk egy egész számú

c

értéket. Azt kell megállapítanunk, hogy mely

c

(ill.

y_{1}

) értéknél kapunk még két egész számú megoldást. Ha az egyenlet gyökei

y_{1}

y_{2}

és

y_{3}

, akkor az (1) egyenlet együtthatói szerint

\begin{matrix} y_{1} + y_{2} + y_{3} = 0, vagyis - (y_{2} + y_{3}) = y_{1}, ezenkívül y_{1} y_{2} y_{3} = - (c - 258) \end{matrix}

és figyelembe véve a (2) egyenletet is

\begin{matrix} y_{1} (y_{1}^{2} - 283) = y_{1} y_{2} y_{3}, tehát y_{2} y_{3} = y_{1}^{2} - 283. \end{matrix}

Eszerint az egyenlet két gyökét meghatározza a

\begin{matrix} z^{2} + y_{1} z + (y_{1}^{2} - 283) = 0 \end{matrix}

egyenlet, ahol

y_{1}

valós egész szám. ¹ Az egyenlet két gyöke is ilyen, ha az egyenlet diszkriminánsa pozitív és teljes négyzet:

\begin{matrix} D \equiv y_{1}^{2} - 4 (y_{1}^{2} - 283) = 1132 - 3 y_{1}^{2} . \end{matrix}

D > 0

, ha

y_{1}^{2} < \frac{1132}{3}

, ill.

| y_{1} | < 20

. Ha zérus és

20

között megvizsgáljuk az egész számokat, mint

y_{1}

abszolút értékeit, azt látjuk, hogy

| y_{1} | = 19

13

és

6

esetében teljes négyzet a diszkrimináns. Ezek közül

- 19

+ 13

és

+ 6

mellett a (2) egyenlet szerint

c - 558 = 1482

, vagyis

c = 2040

, továbbá

+ 19

- 13

és

6

esetében

c - 558 = 1482

, vagyis

c = - 924

. Miután három-három

y

érték mellett ugyanazon

c

értékeket kapjuk, azért ez a két értékcsoport egy-egy harmadfokú egyenletnek a három gyöke. Ezért az eredeti egyenlet keresett alakja

\begin{matrix} x^{3} - 6 x^{2} - 271 x + 2040 = 0, ill. x^{3} - 6 x^{2} - 271 x - 924 = 0. \end{matrix}

Az egyenletek gyökei

x - y + 2

szerint

x_{1} = 17

x_{2} = 15

és

x_{3} = 8

, ill.

x'_{1} = 21

x'_{2} = 11

és

x'_{3} = - 4

Komlós János (áll. gr.Széchenyi István gyak. r. VII. o. Pécs)

II.

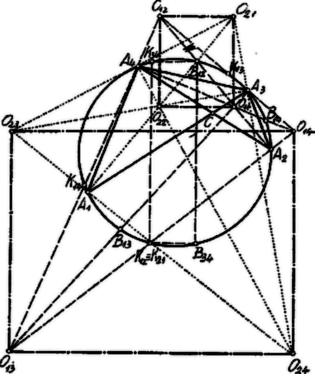
Tekintsük az

A_{1} A_{2} A_{3} A_{4}

húrnégyszög egyenesei által meghatározott

A_{1} A_{2} A_{3}

A_{1} A_{2} A_{4}

A_{1} A_{3} A_{4}

és

A_{2} A_{3} A_{4}

háromszögeket. Bizonyítsuk be, hogy ezen háromszögekbe beírt és hozzáírt körök középpontjai ‐ számszerint

4 \times 4 = 16

‐ négyesével az

A_{1} A_{3}

és

A_{3} A_{4}

átlók szögeinek egymásra merőleges felezőivel párhuzamos

4‐4

egyenesen helyezkednek el.
Bakos Tibor

Megoldás. Az

A_{2} A_{3} A_{4}

háromszög be- és hozzáírt köreinek középpontjai legyenek rendre

O_{11}

O_{12}

O_{13}

O_{14}

(

O_{12}

O_{13}

O_{14}

A_{2}

A_{3}

A_{4}

-ból kiinduló belső szögfelezőn). Az ezeket meghatározó belső és külső szögfelezők minden csúcsban merőlegesek egymásra és így a belső szögfelezők magasságvonalai,

O_{11}

pedig magasságpontja a külső szögfelezők alkotta

O_{12} O_{13} O_{14}

háromszögnek. Megfordítva, ehhez az utóbbihoz az eredeti háromszög mint talpponti háromszög, az eredeti kör (a húrnégyszög körülírt köre) pedig mint ennek körülírt köre, tehát mint Feuerbach-kör tartozik hozzá. Ezért a körnek a belső és külső szögfelezőkkel való második metszéspontjai,

B_{12}

B_{13}

B_{14}

és

K_{12}

K_{13}

K_{14}

mint a Feuerbach-körnek a magasságokkal, illetőleg oldalakkal közös pontjai, felezik a

4

érintőkör középpontja közötti

6

távolságot. Ugyanezek a pontok, mint egy-egy kerületi szög felezőjének a körrel való metszéspontjai, még az illető szög szárai közé eső körívet is felezik ‐ pl.

B_{12}

és

K_{1}

A_{3} A_{1}

íveket ‐ és így az összetartozó párok a háromszög egy-egy oldalára merőleges átmérő végpontjai. Pl.

\bar{B_{12} K_{12}}

A_{3} A_{4}

oldalra merőleges,

B_{12}

A_{2}

-t nem tartalmazó

A_{3} A_{4}

íven van, ez, mint a belső szögfelező metszése, a belső ívfelezőpont,

K_{12}

pedig a külső. A

B_{12}

pont mint az

O_{11} O_{12} A_{3}

és

O_{11} O_{12} A_{4}

derékszögű háromszögek közös átfogójának felezőpontja, mindkét háromszög körülírt körének középpontja, tehát

\begin{matrix} \bar{O_{11} O_{12}} = 2 \cdot \bar{A_{3} B_{12}} = 2 \cdot \bar{A_{4} B_{12}} ... \end{matrix}

(1a)

Hasonlóan

K_{12}

és az

O_{13} O_{14} A_{3}

és

O_{13} O_{14} A_{4}

derékszögű háromszögek révén

\begin{matrix} \bar{O_{13} O_{14}} = 2 \cdot \bar{A_{3} K_{12}} = 2 \cdot \bar{A_{4} K_{12}} ... \end{matrix}

(1b)

Tekintsük most az

A_{2} A_{3} A_{4}

háromszöget. Az előzőkhöz hasonlóan és azonos jelölésmóddal ,,1" és ,,2'' indexeket felcserélve

\begin{matrix} \bar{O_{22} O_{21}} = 2 \cdot \bar{A_{3} B_{21}} = 2 \cdot \bar{A_{4} B_{21}} valamint\bar{O_{23} O_{24}}= 2\cdotA_{3}K_{21}= 2\cdot\bar{A_{4} K_{21}}. \end{matrix}

Mivel azonban

A_{1}

ugyanazon az

A_{3} A_{4}

íven van, mint

A_{2}

, számára belső és külső ívfelezőpont ugyanaz, mint

A_{2}

-nél, azért a

B_{21}

és

B_{12}

, valamint

K_{21}

és

K_{12}

pontok azonosak és így

\begin{matrix} \bar{O_{22} O_{21}} = 2 \cdot \bar{A_{3} B_{12}} = 2 \cdot \bar{A_{1} B_{12}} ... és & (2a) \\ \bar{O_{23} O_{24}} = 2 \cdot A_{3} K_{12} = 2 \cdot \bar{A_{4} K_{12}} ... & (2b) \end{matrix}

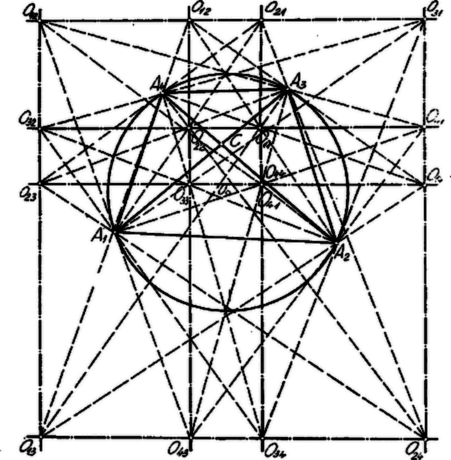
(1a) és (2a), valamint (1b) és (2b) szerint az

\bar{O_{11} O_{12}}

és

\bar{O_{22} O_{21}}

, valamint

\bar{O_{13} O_{14}}

és

\bar{O_{23} O_{24}}

távolságok egyenlők és felezik egymást (ugyanis felezőpontjaik

B_{12}

és

K_{12}

azonosak) és így végpontjaik egy-egy derékszögű egyenlő közű négyszög csúcsai.
Állapítsuk meg ezekben a téglalapokban az oldalak irányait az eredeti húrnégyszöghöz viszonyítva! Felhasználjuk azt, hogy téglalap oldalai párhuzamosak átlóinak szögfelezőivel, továbbá azt, hogy, ha

e_{1} ⊥ f_{1}

, és

e_{2} ⊥ f_{2}

, akkor az

e_{1}

e_{2}

, valamint

f_{1}

f_{2}

egyenespárok alkotta szögek felezői is párhuzamosak, illetve merőlegesek.
Téglalapjaink átlóinak egyik-egyik szöge szerkesztés folytán az

A_{1} A_{2}

ívek valamelyikén nyugvó kerületi szög, felezőik eszerint átmennek ezeknek az íveknek

B_{34}

illetőleg

K_{34}

felezőpontjain és így az

O_{11} O_{12} O_{22} O_{21}

, téglalap oldalai egyirányúak

\bar{B_{12} B_{34}}

és

\bar{B_{12} K_{34}}

, az

O_{13} O_{24} O_{14} O_{23}

pedig

K_{12} B_{34}

és

\bar{K_{12} K_{34}}

-gyel. Sőt mivel az itt szereplő négy pont alkotta négyszög átlói átmérők, az maga is téglalap, ezért eredeti téglalapjaink oldalai egymással is és a

B_{12} B_{34} K_{12} K_{34}

téglalap oldalaival, és így átlóinak szögfelezőivel is párhuzamosak. Ezek az átlók viszont a korábbiak szerint merőlegesek a húrnégyszög szembenfekvő

A_{1} A_{2}

és

A_{3} A_{4}

oldalaira, és így a keresett irányok az előre idézett segédtételnél fogva párhuzamosak azoknak a szögeknek a felezőivel, amelyeket az említett oldalak meghosszabbításai alkotnak és az 1214. feladat szerint az átlók szögfelezőivel is.^{$^{*}$}

Az átlók metszéspontját

C

-vel, az

A_{1} C A_{2}

és

A_{2} C A_{3}

szögek felezőit pedig

f_{1}

és

f_{2}

-vel jelölve eddigi eredményünk így írható:

\begin{matrix} \bar{O_{11} O_{21}}, \bar{O_{12} O_{22}}, \bar{O_{13} O_{23}}, \bar{O_{14} O_{24}} párhuzamosak f_{1} -gyel , \end{matrix}

\begin{matrix} \bar{O_{11} O_{22}}, \bar{O_{12} O_{21}}, \bar{O_{13} O_{24}}, \bar{O_{14} O_{23}} párhuzamosak f_{2} -vel \end{matrix}

Ezekből az indexek ciklikus permutációjával még a következők adódnak:

\begin{matrix} \bar{O_{22} O_{33}}, \bar{O_{23} O_{32}}, \bar{O_{24} O_{31}}, \bar{O_{21} O_{34}}, \bar{O_{33} O_{43}}, \bar{O_{34} O_{44}}, \bar{O_{31} O_{41}}, \bar{O_{32} O_{42}}, \bar{O_{44} O_{11}}, \bar{O_{41} O_{14}}, \bar{O_{42} O_{13}}, \bar{O_{43} O_{12}} \end{matrix}

párhuzamosak

f_{1}

-gyel,

\begin{matrix} \bar{O_{22} O_{32}}, \bar{O_{23} O_{33}}, \bar{O_{24} O_{34}}, \bar{O_{21} O_{31}}, \bar{O_{33} O_{44}}, \bar{O_{34} O_{43}}, \bar{O_{31} O_{42}}, \bar{O_{32} O_{41}}, \bar{O_{44} O_{14}}, \bar{O_{41} O_{11}}, \bar{O_{42} O_{12}}, \bar{O_{43} O_{13}}, \end{matrix}

párhuzamosak

f_{2}

-vel,
Ebben a felsorolásban minden középpont négyszer lép fel és pedig a két egymásra merőleges irány mindegyike mentén kétszer-kétszer. A

16 - 16

egyirányú távolság négyes csoportokra osztható úgy, hogy egy-egy csoport távolságait ugyanaz a négy pont határolja, amiből nyilvánvaló, hogy az illető négy pont egy egyenesen fekszik. Így pl. mivel

\bar{O_{13} O_{23}}

\bar{O_{23} O_{32}}

\bar{O_{32} O_{42}}

és

\bar{O_{42} O_{13}}

mind párhuzamosak

f_{1}

-gyel és így egymással is, azért

O_{13}

O_{23}

O_{32}

és

O_{42}

egy az

f_{1}

-gyel párhuzamos egyenes pontjai.

B. T.

III.

Igazoljuk, hogy ha egy derékszögű parallelepipedonnak,

P

-nek, négy nem ugyanegy síkban fekvő csúcsa négy koncentrikus gömbön mozog, akkor annak a többi négy csúcsa is amazokkal közös középpontú gömbön mozog, még akkor is, ha

P

-nek alakja változik. E nyolc gömb közül több egybe eshetik, és pedig, ha

P

-nek:
a) egy élen levő két csúcsa ugyan egy gömbön mozog, akkor ez éllel parallel három élen levő két-két csúcs szintén egy-egy gömbön mozog;
b) egy lapján levő három csúcsa ugyanegy gömbön mozog, akkor e lapon levő negyedik csúcs is e gömbön marad, míg a többi 4 csúcs egy másik gömbön lesz;
c) három csúcsa, melyek közül kettő szemben fekvő, ugyanegy gömbön mozog, akkor a harmadik csúccsal szemben fekvő csúcs is e gömbön marad, míg a többi négy csúcs páronként két másik gömbön mozog;
d) három olyan csúcsa, melynek síkjában a

P

-nek nincs több csúcsa, egy gömbön mozog, akkor

P

-nek ezzel szemben fekvő három csúcsa egy másik gömbön mozog, míg a hátralevő szembenfekvő két csúcs egy-egy gömböt ír le;
e) a négy mozgó csúcsa ugyanegy gömbön marad, akkor ugyanegy gömbön marad

P

-nek többi négy csúcsa is.

Klug

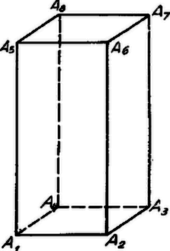
Megoldás. Legyen a gömbök középpontja

O

, és

P

-nek négy nem egy síkban fekvő csúcsa

A_{1}

A_{2}

A_{3}

, és

A_{6}

. Az

O

pontból

P

-nek tetszés szerinti helyzetében a

A_{1}

A_{2}

A_{3}

síkra bocsátott merőleges talppontját jelölje

M

. Ha az

A_{1} A_{2} A_{3}

, síkban fekvő negyedik csúcs

A_{4}

, akkor mint ismeretes,^{$^{*}$} a síkban fekvő bármely pontra, és így

M

-re nézve is fennáll:

{\bar{M A}}_{1}^{2} + {\bar{M A}}_{3}^{2} = M A_{2}^{2} + M A_{4}^{2}

(ha

A_{1}

és

A_{3}

a téglalap szembenfekvő csúcsai).
Ezenkívül pedig

\begin{matrix} {\bar{O A}}_{1}^{2} + {\bar{O A}}_{3}^{2} = ({\bar{M A}}_{1}^{2} + {\bar{O M}}^{2}) + ({\bar{M A}}_{3}^{2} + {\bar{O M}}^{2}) = {\bar{M A}}_{1}^{2} + {M A}_{3}^{2} + 2 \cdot {\bar{O M}}^{2} és \\ {\bar{O A}}_{2}^{2} + {\bar{O A}}_{4}^{2} = ({\bar{M A}}_{2}^{2} + {\bar{O M}}^{2}) + ({\bar{M A}}_{4}^{2} + {\bar{O M}}^{2}) = = {\bar{M A}}_{2}^{2} + {\bar{M A}}_{4}^{2} + 2 \cdot {O M}^{2} . \end{matrix}

Az egyenletek szerint

\begin{matrix} {\bar{O A}}_{1}^{2} + {\bar{O A}}_{3}^{2} = {O A}_{2}^{2} + {\bar{O A}}_{4}^{2} \end{matrix}

^{$^{*}$}
ami azt fejezi ki, hogy ha

O A_{1}

és

O A_{2}

és

O A_{3}

állandó távolságok, akkor állandó

O A_{4}

is. E szerint az

A_{4}

csúcs is egy

O

középpontú gömbön mozog. Hasonlóképpen, ha az

A_{1} A_{2} A_{6}

síkban fekvő negyedik csúcs

A_{5}

, mivel

O A_{1}

O A_{2}

, és

O A_{6}

állandó, nem változik az

O A_{5}

távolság sem. Ugyancsak ez a helyzet az

A_{2} A_{3} A_{6}

síkban fekvő

A_{7}

pontnál is. Mivel most már tudjuk, hogy

O A_{5}

O A_{6}

és

O A_{7}

is állandó távolságok, bizonyítva van, hogy

O A_{8}

is állandó. Látjuk tehát, hogy a nyolc pont általában nyolc koncentrikus gömbön mozog.
Különös esetek:
a) Az

A_{1}

és

A_{2}

csúcs egy gömbön mozog, azaz

O A_{1} = O A_{2}

. Láttuk, hogy

\begin{matrix} {\bar{O A}}_{1}^{2} + {\bar{O A}}_{3}^{2} = {\bar{O A}}_{2}^{2} + {\bar{O A}}_{4}^{2}, tehát O A_{3} = O A_{4}, \\ {\bar{O A}}_{1}^{2} + {\bar{O A}}_{6}^{2} = {\bar{O A}}_{2}^{2} + {\bar{O A}}_{5}^{2}, tehát O A_{5} = O A_{6}, \\ {\bar{O A}}_{1}^{2} + {\bar{O A}}_{7}^{2} + {\bar{O A}}_{2}^{2} + {\bar{O A}}_{8}^{2}, tehát O A_{7} = O A_{8}, \end{matrix}

vagyis:

A_{3}

és

A_{4}

A_{5}

és

A_{6}

A_{7}

, és

A_{8}

egy-egy gömbön maradnak.
b) Az

A_{1}

A_{2}

és

A_{3}

csúcsok egy gömbön maradnak. Az a) eset szerint, ha

O A_{1} = O A_{2}

akkor

O A_{3} = O A_{4}

vagyis az egy lapon lévő négy csúcs egy gömbön mozog. Ugyancsak az a) esetből következik, hogy

O A_{5} = O A_{6}

és

O A_{7} = O A_{8}

, de mivel

O A_{6} = O A_{7}

, azért a másik lapon fekvő négy csúcshoz is egyenlő sugarak tartoznak.
c)

A_{1}

és

A_{7}

szembenfekvő csúcsok, továbbá

A_{2}

is egy gömbön mozog. Mivel az

A_{1} A_{2}

éllel párhuzamos

A_{7} A_{8}

, azért az

A_{8}

csúcs is a három említett csúccsal egy gömbön van, míg

A_{3}

és

A_{4}

továbbá

A_{5}

és

A_{6}

egy gömbön mozog.
d)

A_{1}

A_{3}

és

A_{6}

egy gömbén mozog. Az első esettel megegyező módon bebizonyíthatjuk azt is, hogy ha valamelyik lap átlóján lévő két csúcs egy gömbön mozog, akkor az ezzel párhuzamos átlón levő két csúcs is egy gömbön marad. Eszerint egy gömbön van

A_{5}

és

A_{7}

A_{4}

és

A_{5}

, továbbá

A_{4}

és

A_{7}

ill. egy gömbön mozog

A_{4}

A_{5}

és

A_{7}

. Az

A_{2}

és

A_{8}

ha egyéb feltétel nincs, külön gömbökön mozognak.
e) Az

A_{1}

A_{2}

A_{3}

és

A_{6}

csúcs mozogjon egy gömbön. Az a esetben bizonyítottakat figyelembe véve

A_{1}

csúccsal azonos gömbön van

A_{4}

és

A_{5}

, az

A_{6}

csúccsal

A_{7}

. Így

A_{5}

és

A_{8}

is ugyanazon gömbön mozog. Ezeket összevetve azt kapjuk, hogy mind a nyolc csúcs ugyanazon a gömbön mozog. (Csak négy nem egy síkban fekvő esetében áll fenn.)

Komlós János (áll. gr. Széchenyi István gyak. r. VII. o. Pécs)

Jegyzet. Négy nem egy síkban fekvő csúcspontot úgy is kiszemelhetünk, hogy kettőt az alapsíkról, kettőt a fedőlap síkjáról, mint két kitérő átló végpontjait vesszük. Pl.

A_{1}

A_{3}

A_{8}

A_{6}

.
Ebben az esetben is ugyanazon eredményre jutunk. T. i. az

\begin{matrix} {\bar{O A}}_{1}^{2} + {\bar{O A}}_{3}^{2} = {\bar{O A}}_{2}^{2} + {\bar{O A}}_{4}^{2} és {\bar{O A}}_{2}^{2} + {\bar{O A}}_{8}^{2} = {\bar{O A}}_{6}^{2} + {\bar{O A}}_{4}^{2} \end{matrix}

egyenletekből következik, hogy ha

O A_{1}

O A_{3}

A O_{6}

A O_{8}

állandó távolságok, akkor

O A_{2}

és

O A_{4}

is azok. Hasonlóan mutatható ki, hogy

O A_{5}

és

O A_{7}

is állandó értékek.

.......................

Közlésünkből kitűnik, hogy mindhárom tételt ketten oldották meg: Komlós János és Nagy Elemér (ciszterci Szent Imre reálgimn. VII. o. Bp.)
Tekintettel arra, hogy Komlós János különösen az I. tételt oldotta meg rövidebben és ügyesebben, neki ítéljük első díj gyanánt KÜRSCHÁK "Matemetikai versenytételek" c. művét. Mint második díjat, folyóiratunk II. évfolyamát Nagy Elemérnek adjuk.
A II. tétel megoldásaként a kitűzőét közöltük.
Szerk

¹Ezen egyenletben

y_{1}

helyett írható

y_{2}

, ill.

y_{3}

. Ebből következik, hogy ezek abszolút értékei

19

13

6

. Minthogy

\begin{matrix} y_{1} + y_{2} + y_{3} = 0, vagy -19+13+6=0 vagy 19-13-6=0. \end{matrix}

^{$^{*}$}I. XII. évf. 261.o. (1936/5 ‐ a szerk.)

^{$^{*}$}L: 1003 gyakorlat (XII. évf. 2.szám ‐1935/10. 42. old.)

^{$^{*}$}Ilyen összefüggés érvényes bármely $4$ olyan szögpontra, amelyek egy téglalap csúcsai, tehát pl. az $A_{1}$ , $A_{2}$ , $A_{7}$ , $A_{8}$ szögpontokra is.