Cím: 1936. A XL. Eötvös Loránd matematikai tanulóverseny tételei - 2.
Füzet: 1937/január, 129 - 135. oldal  PDF  |  MathML 
Témakör(ök): Kürschák József (korábban Eötvös Loránd)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

a) A XL. Eötvös Loránd matematikai tanuló-verseny tételei

 
I.

 
Bebizonyítandó, hogy
11⋅2+13⋅4+15⋅6+...+2(2n-1)2n=1n+1+1n+2+1n+3+...+12n.

I. Megoldás.
 
Ha  n=1,11⋅2=1-12=12.
n=2mellett11⋅2+13⋅4=12+13-14-12+13+14-12=13+14.

n=3esetében11⋅2+13⋅4+15⋅6=13+14+15-16=13+14+15+16-13=
=14+15+16.

Tegyük fel, hogy a tétel igaz n-re, azaz
Sn≡11⋅2+13⋅4+15⋅6+...+1(2n-1)2n=1n+1+1n+2+1n+3+...+12n.
Kimutatjuk, hogy a tétel igaz n+1-re is. Ugyanis
Sn+1≡Sn+1(2n+1)(2n+2)==1n+1+1n+2+1n+3+...+12n+(12n+1-12n+2).



Azonban12n+1-12n+2=12n+1+12n+2-1n+1.

Ennek tekintetbe vételével, az egyenlet jobboldalán elmarad 1n+1
és ígySn+1=1n+2+1n+3+...+12n+12n+1+12n+2,

azaz Sn+1 képezésének törvénye megegyezik Sn törvényével.
Minthogy a tétel igaz, ha n=1,2,3, igaz az n bármely értéke mellett.
 
Almássy György (Kegyesrendi g. VIII. o. Veszprém).

 
II. Megoldás. Minthogy (az előbbiek szerint)
1(2x-1)2x=12x-1-12x=12x-1+12x-1x,
a bebizonyítandó egyenlőség baloldala
∑1n(12x-1+12x)-∑1n1x
alakban írható. Azonban
∑1n(12x-1+12x)=∑12n1x,
mert ∑1n12x-1 a 2n-nél kisebb páratlan számok reciprok értékeinek és
∑1n12x 2n-nél nem nagyobb páros számok reciprok értékeinek összege és így a két összeg együttesen az 1-től 2n-ig haladó összes egész számok reciprok értékeinek összege. Eszerint a szóbanforgó összeg valóban
∑12n1x-∑1n1x=∑n+12n1x=1n+1+...+12n.Harsányi János, (Ág. ev. g. VIII. o. Bp).

 

II.

 

 

Legyen az ABCΔ-ön belül választott S pont oly tulajdonságú, hogy az ABS, BCS, CAS háromszögek megegyező területűek. Bebizonyítandó, hogy S az ABCΔ súlypontja.
 

I. Megoldás. A háromszög S súlypontja az AA1, BB1, CC1, oldalfelező transzverzálisoknak (súlyvonalak) közös pontja.
Az AA1 súlyvonal az ABCΔ-et és a BCSΔ-et is két egyenlő területű részre osztja.
Az ABCΔ két része: ACA1 és ABA1 területre egyenlők, mert alapjuk egyenlő: A1C=A1B és ehhez tartozó magasságuk, AH, közös.
A BCSΔ két része: BSA1 és CSA1 területre egyenlők, mert alapjuk egye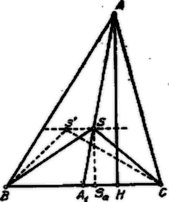nlő: A1C=A1B és ehhez tartozó magasságuk, SSa közös.
 
 

Ebből következik, hogy az ABA1 és BSA1 háromszögek területének különbsége egyenlő az ACA1 és CSA1 háromszög területének különbségével, azaz
tABS=tCAS.

Hasonlóan következik, a BB1 súlyvonal segítségével, hogy
tABS=tBCS.

Eszerint a háromszög S súlypontja oly tulajdonságú, hogy
tABS=tBCS=tCAS=13tABC.

Tegyük fel, hogy volna még egy S-től különböző S' pont, amely ugyanolyan tulajdonságú, mint S, azaz
tABS'=tBCS'=tCAS'=13tABC.

Ebben az esetben tABS'=tABS; ez csak úgy lehetséges, hogy mivel e két háromszögnek közös alapja van, ha a magasságuk is egyenlő, vagyis SS'∥AB.
Ugyanígy tBCS'=tBCS'; ebből pedig SS∥BC.
Azonban SS'∥AB és SS'∥BC ellentmondás.
Tehát más pont, mint az S súlypont, nem bírhat a szóbanforgó tulajdonsággal.
 

II. Megoldás. Az S súlypont tulajdonságát előbb bebizonyítottuk.
Tegyük fel, hogy az S-től különböző S' pont ugyanolyan tulajdonságú, mint az S súlypont. Ezen S' pont akkor beleesik pl. az ABSΔ-be (ill. ennek AS vagy BS oldalára). Ekkor pedig
tABS'<tABSazaztABS'<13tABC.

Kell tehát, hogy tBCS', vagy tCAS' nagyobb legyen, mint 13tABC, azaz: S' nem bonthatja fel az ABCΔ-et három egyenlő területű részre.
 

Kemény György (áll. Szent István rg. VII. o. Bp. XIV.)

Oroszhegyi Szabó Lajos (Kegyesrendi g. VIII. o. Bp. IV.)

 

III. Megoldás. Ha a BCS és ABS háromszögek területe egyenlő, akkor, mivel BS-t közös alapnak tekinthetjük, kell, hogy az ehhez tartozó magasságok is egyenlők legyenek: AK=CL. Ebből azonban következik, hogy ha BS az AC-t a B1-ben metszi, AB1KΔC∞B1LΔ. Ugyanis K∢=L∢=90∘, továbbá az AK és CL befogókkal szembenfekvő szögek, mint csúcsszögek, egyenlők.
Ebből következik: AB1=CB1 azaz az S pont a BB1 oldalfelezőn (súlyvonalon) fekszik.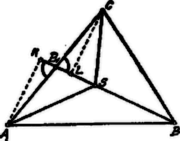
 
 

Hasonló meggondolással következik, hogy S az AA1 ill. CC1 oldalfelezőkön is rajta fekszik, tehát S a háromszög súlypontja.
 

Sebestyén Gyula (Fazekas Mihály r. VII. o. Debrecen).

 

IV. Megoldás. Legyen az S pont olyan tulajdonságú, hogy
tABS=tBCS=tCAS=13tABC.

Az ABS és ABC háromszögeknek közös alapja AB; az elsőnek magassága SSc, a másodiké CD=mc. Mint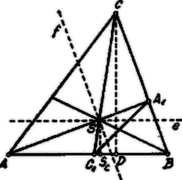hogy
tABS=13tABC,kell, hogySSc=13CD=13mclegyen.

 

Eszerint kell, hogy S az AB oldallal párhuzamos e egyenesen feküdjék, melynek távolsága AB-től 13mc.1
Hasonlóan S a BC oldallal párhuzamos f egyenesen is fekszik, melynek távolsága BC-től 13ma.
e és f egyenesek meghatározzák az S pontot. Azt kell még kimutatnunk ‐ és ez elegendő is ‐ hogy AS és CS súlyvonalak.
Húzzuk meg az AS egyenest, mely BC-t az A1, továbbá a CS egyenest, mely AB-t a C1 pontban metszi.
Nyilván
SA1=13AA1ésSC1=13CC1
ill.
AS:SA1=2:1ésCS:SC1=2:1,azazAS:SA1=CS:SC1.

Ebből következik, hogy ASCΔ∼A1S1CΔ, mert: az S csúcsnál egyenlő szögük van és ezen szöget bezáró oldalak aránya egyenlő. Kimondhatjuk tehát, hogy SA1C1∢=SAC∢,
ill.
A1C1∥ACésA1C1=12AC.

Ez azonban azt jelenti, hogy A1 a BC, C1 az AB oldal felezőpontja: AA1 és CC1 súlyvonalak és így S az ABCΔ súlypontja.
 

Kádár Géza (Dobó István r. VII. o. Eger)

 

V. Megoldás. Derékszögű koordinátarendszerünk kezdőpontját helyezzük abba az S pontba, amelyre nézve
tABS=tBCS=tCAS...(1)

 
 

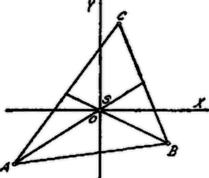Az A, B, C csúcsok a pozitív forgás irányában következnek egymás után, (x1,y1), (x2,y2), (x3,y3) koordinátákkal. Így az 1) feltétel
x1y2-x2y1=x2y3-y2x3=x3y1-x1y3...(2)
alakban írható és innen
(x1+x3)y2=(y1+y3)x2...(2a)
ill.
(x2+x1)y3=(y2+y1)x3...(2b)
vagy még
(x3+x2)y1=(y3+y2)x1...(2c)

Már most ezen összefüggések azonosak a következőkkel:

(x1+x2+x3)y2=(y1+y2+y3)x2azazy2x2=y1+y2+y3x1+x2+x3...(3a)(x1+x2+x3)y3=(y1+y2+y3)x3a,,zy3x3=y1+y2+y3x1+x2+x3...,(3b)(x1+x2+x3)y1=(y1+y2+y3)x1a,,zy1x1=y1+y2+y3x1+x2+x3....(3c)

A (3a), (3b), (3c) egyenletek azonban azt fejezik ki, hogy az SB, SC, SA egyenesek keresztül mennek a háromszög súlypontján, mert
x1+x2+x33,y1+y2+y33.
a háromszög súlypontjának koordinátái. Tehát S pont a háromszög súlypontja.
 

Jegyzet. A felsorolt megoldásokon kívül még számos dolgozat érkezett, különösen a IV. megoldásra, amelyek nem voltak figyelembe vehetők. Ugyanis ezen dolgozatok éppen azt mellőzik, amit bizonyítanunk kell. Nem szabad egyszerűen azt állítani, hogy mivel az S pontra nézve SSc=31mc s. í. t., ez az S pont nem lehet más, mint a súlypont.
Ugyancsak nem voltak figyelembe vehetők az analitikai módszerrel dolgozók közül azok, amelyek a szóbanforgó területek egyenlőségének felírása után kijelentik, hogy az egyenletrendszer megoldása
x1+x2+x33,y1+y2+y33.

Valóban ezen megoldás sok és kényelmetlen számítással járna. Ebből csak az a tanulság, hogy kerüljük az ilyen eljárásokat. Helyesen jártak el azok, akik a koordinátarendszer kezdőpontját a háromszög egyik csúcsába, az egyik tengelyen pedig a háromszög egyik oldalát helyezték el.
 

III.

 

Legyen ,,a'' egy tetszőlegesen adott pozitív egész szám. Bebizonyítandó, hogy mindig van egy és pedig csakis egy pozitív egész x, y számokból álló (x,y) számpár, amelyre
x+(x+y-1)(x+y-2)2=a.

I. Megoldás. Legyen
x+y-1=k,tehátx+y-2=k-1...(1)
és vizsgáljuk az adott a számnak a
k(k-1)2...(2)
alakú egész számok sorához viszonyított helyzetét.1
Két eset lehetséges: a vagy előfordul ezen számok sorában, vagy a számsor két tagja között van.
Az első esetben a k poz. egész szám megállapítható úgy, hogy
a=(k+1)k2,azazx=(k+1)k2-k(k-1)2=k
és ekkor, mivel x+y-1=k, x=k mellett y=1, tehát egyenletünket a (k,1) számpár kielégíti.
A második esetben k meghatározható úgy, hogy
k(k-1)2<a<(k+1)k2,...(3)
és ekkor
0<x<k,t. i.x=a-k(k-1)2=α,
azaz létezik egy x=α poz. egész szám úgy, hogy 1≤α<k,


és így
y=k+1-α>0,
egyenletünket tehát az (a,k+1-α¯) számpár elégíti ki.
A két eset egybefoglalásával mondhatjuk: 1≤α≤k.
Már most azt kell kimutatnunk, hogy egyenletünket több pozitív egész számokból álló számpár nem elégítheti ki. Nézzük tehát az a számnak a 2) sorozat azon tagjaihoz való helyzetét, melyek k(k-1)2-t megelőzik!1 Így
a=k(k-1)2+α=(k-1)(k-2)2+k-1+α,
azaz most
x=k-1+α>0;
azonban, mivel
x+y-1=k-1,y=k-x=k-(k-1+α)=1-α≤0,


tehát már nem kapunk pozitív y-t.
Általában, mivel
a=k(k-1)2+α=(k-i)(k-i-1)2+α+(k-1)+(k-2)+...+(k-i)ési<k,


azért
x=α+ik-i(i+1)2>0.
Azonban most
x+y-1=k-i,
tehát
y=1+(k-i)-x=1+(k-i)-α-ik+i(i+1)2,y=1-α-(i-1)(k-i2)<0.

 

II. Megoldás. Ha be tudjuk bizonyítani, hogy a pozitív egész x, y számokból (x,y) számpár összes lehető változatainak megfelelő rendezésével
f(x,y)≡x+(x+y-1)(x+y-2)2
kifejezés a pozitív számsor összes egész számait adja, 1-től kezdődőleg, egyszer és csak egyszer, akkor bebizonyítottuk, hogy mindig van egy és csakis egy pozitív egész (x,y) számokból álló (x,y,) számpár, amely a követelménynek megfelel. Legyen ugyanis x+y=c, állandó, akkor f(x,y)=a csak az x-től függ úgy, hogy amint x növekedik egy-egy egységgel, úgy növekedik a is egy-egy egységgel. Tehát az (x,y) számpár ama változataihoz, melyek az x+y=c feltételnek megfelelnek, a pozitív egész számsor egymásután következő tagjainak egy bizonyos része felel meg egyszer és csak egyszer.1
Ha bebizonyítjuk, hogy az (x,y) számpár változatainak következő csoportjához, amelyre nézve x+y=c+1, a pozitív egész számsornak az előbbieket közvetlenül követő csoportja felel meg, akkor beláthatjuk, hogy ha az (x,y) számpár változatait így rendszerezve helyettesítjük f(x,y) kifejezésbe, akkor valóban a pozitív egész számok teljes sorát kapjuk, egymásután, egyszer és csak egyszer, 1-től kezdődőleg. Ugyanis, ha x=1, y=1, akkor a=1.
Az x+y=c csoport utolsó számpárja az x=1, 2, ...c-1 sorrendben haladva (c-1¯,1). x>c nem lehet, mert akkor y≤0. A következő x+y=c+1 csoport első számpárja 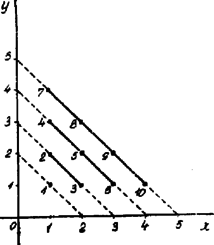(1,c).
A(c-1,¯1)számpárral
f(x,y)=c-1+(c-1)(c-2)2,azaza1=c2-c2.
Az (1,c) számpárral
f(x,y)=1+c(c-1)2azaza2=1+c2-c2
tehát
a2=a1+1.

 
 

Látjuk ebből, hogy az x+y=c csoport utolsó számpárjának megfelelő egész szám a1 és az utána következő egész szám, a2, tényleg a következő csoport első (x,y) számpárjához tartozó szám.
Ezzel tehát állításunkat bebizonyítottuk. Minthogy x+y=c oly egyenesnek egyenlete, mely a tengelyekről c darabot vág le, ezen egyenesek mentén feküsznek az (x,y) számpárokhoz tartozó a egész számok. A kezdő szám a=1 az x+y=2 egyenesen fekszik. Az x+y=c egyenesnek a tengelyeken fekvő pontjai már nem határoznak meg a számot.
 

Weisz Alfréd (Bolyai r. VII. o. Bp. V.)
1Ilyen egyenes kettő van: azt kell vennünk, mely az AB azon oldalán fekszik, amelyen a C csúcs.

1E sorozat tagjai:  0,  1,1 3,  6,  10,  15,  21,  28  ... 
másodrendű számtani haladványt alkotnak, az egymásután következő tagok különbségei 1,  2,  3,  4,  5,  ...elsőrendű számtani haladványt.

1Ha azokat tekintjük, amelyek k(k-1)2 után következnek, akkor már x<0.

1Ezen tagok száma: c-1, mert, ha x+y=c, akkor x=1, 2, ... c-1