Kezdőlap


Cím:	A Stewart-tétel és alkalmazása
Szerző(k):	Dr. Kresznerics Károly
Füzet:	1937/március, 193 - 196. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A Stewart¹-tétel és alkalmazása.

A B C

háromszögnek

A B

oldalán fekvő tetszőleges

X

pontot kössük össze a szembenfekvő

C

csúcsponttal, akkor a Pythagoras-tétel értelmében: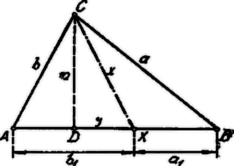

\begin{matrix} a^{2} = m^{2} + {(a_{1} + y)}^{2}, \\ b^{2} = m^{2} + {(b_{1} - y)}^{2}, \\ x^{2} = m^{2} + y^{2} . \end{matrix}

E három egyenletből

m

és

y

kiküszöbölésével előállítunk egy egyenletet, amelyből

x

értéke kiszámítható. Evégből a harmadik egyenletből

m^{2} = x^{2} - y^{2}

értékét az első és második egyenletbe helyettesítjük:

\begin{matrix} a^{2} = x^{2} + a_{1}^{2} + 2 a_{1} y, b^{2} = x^{2} + b_{1}^{2} - 2 b_{1} y . \end{matrix}

Szorozzuk meg az első egyenletet

b_{1}

-gyel, a másodikat

a_{1}

-gyel, ezután adjuk össze őket és vegyük figyelembe, hogy

a_{1} + b_{1} = c

, akkor kapjuk Stewart-tételét:

\begin{matrix} (x^{2} + a_{1} b_{1}) c = a^{2} b_{1} + b^{2} a_{1} . \end{matrix}

Szavakkal kifejezve: ha valamely háromszög egyik oldalának tetszőleges pontját összekötjük a szembenfekvő csúcsponttal, akkor az összekötő távolság négyzetéből és az oldal két szeletének szorzatából alkotott összeg szorozva az illető oldallal, egyenlő a második két oldal négyzetének összegével, mindegyik összeadandó szorozva az első oldalon fekvő nem szomszédos szelettel.²
Ezután alkalmazzuk a tételt néhány egyszerű esetben.

1. A súlyvonal hossza.
Ekkor az 1. ábrában

a_{1} = b_{1} = \frac{c}{2}

és

x = s_{c}

, így Stewart tétele értelmében:

\begin{matrix} (s_{c}^{2} + \frac{c^{2}}{4}) c = a^{2} \frac{c}{2} + b^{2} \frac{c}{2}, \end{matrix}

amiből

\begin{matrix} s_{c} = \frac{1}{2} \sqrt[]{2 (a^{2} + b^{2}) - c^{2}} . \end{matrix}

2. A szögfelezők hossza.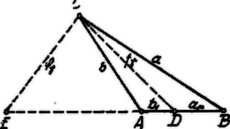

Ismeretes, hogy a belső szögfelező a szöggel szembenfekvő oldalt, a külső szögfelező pedig a szöggel szembenfekvő oldal meghosszabbítását a szöget befogó oldalak arányában osztja. Ebből a két arányból kapjuk:

\begin{matrix} A D = \frac{b c}{a + b}, B D = \frac{a c}{a + b}, \\ E A = \frac{b c}{a - b}, E B = \frac{a c}{a - b} ... \end{matrix}

(I.)

A B C

háromszögben a Stewart-tétel értelmében:

\begin{matrix} (C D^{2} + A D \cdot B D) \cdot A B = A C^{2} \cdot B D + B C^{2} \cdot A D, \end{matrix}

vagyis ha

C D = f_{γ}

, akkor I. figyelembevételével:

\begin{matrix} (f_{γ}^{2} + \frac{b c}{a + b} \cdot \frac{a c}{a + b}) c = b^{2} \frac{a c}{a + b} + a^{2} \frac{b c}{a + b}; \end{matrix}

ebből

\begin{matrix} {(a + b)}^{2} f_{γ}^{2} = a b [{(a + b)}^{2} - c^{2}] ... \end{matrix}

(II.)

azaz

\begin{matrix} f_{γ}^{2} = a b - a b c \frac{c}{{(a + b)}^{2}} . \end{matrix}

Más alakját kapjuk a szögfelező képletének, ha a Heron-féle jelöléseket alkalmazzuk. A II.-ből:

\begin{matrix} {(a + b)}^{2} f_{γ}^{2} = a b (a + b + c) (a + b - c) . \end{matrix}

Ebből a belső szögfelező hossza, ha

a + b + c = 2 s

és

a + b - c = 2 (s - c

)-t helyettesítünk:

\begin{matrix} f_{γ} = \frac{2}{a + b} \sqrt[]{s (s - c) a b} . \end{matrix}

Hasonlóképpen kapjuk a külső szögfelező hosszát. Evégből felírjuk az

E B C

háromszög

A C

szelőjére a Stewart-tételt:

\begin{matrix} (A C^{2} + E A \cdot A B) \cdot E B = E C^{2} \cdot A B + B C^{2} \cdot E A, \end{matrix}

vagyis, ha

E C = φ_{γ}

és I.-re tekintettel vagyunk:

\begin{matrix} (b^{2} + \frac{b c}{a - b} c) \frac{a c}{a - b} = φ_{γ}^{2} c + a^{2} \frac{b c}{a - b} . \end{matrix}

Ebből az előbbihez hasonló átalakítással:

\begin{matrix} φ_{γ}^{2} = a b c \frac{c}{{(a - b)}^{2}} - a b, \end{matrix}

vagy

\begin{matrix} φ_{γ} = \frac{2}{a - b} \sqrt[]{(s - a) (s - b) a b} . \end{matrix}

3. Egy parallelogramma-tétel és megfordítása.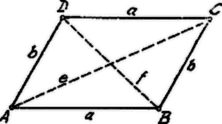

A B D

háromszögben a Stewart-tétel értelmében:

\begin{matrix} (\frac{e^{2}}{4} + \frac{f^{2}}{4}) f = a^{2} \frac{f}{2} + b^{2} \frac{f}{2}, \end{matrix}

ahol

e

és

f

az átlókat jelentik.
Ebből 4-gyel szorzás és az

f

tényezővel való osztás után keletkezik:

\begin{matrix} 2 a^{2} + 2 b^{2} = e^{2} + f^{2} . \end{matrix}

Tehát minden parallelogrammában az oldalak négyzetének összege egyenlő az átlók négyzetének összegével.
A tétel meg is fordítható: ha egy négyszögben az oldalak négyzetének összege egyenlő az átlók négyzetének összegével, akkor a négyszög parallelogramma.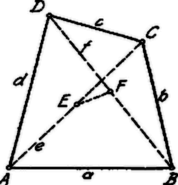

A megfordítást úgy igazoljuk, hogy az adott

A B C D

négyszögben az átlók

E, F

felezőpontjainak egymástól való

E F

távolságát számítjuk ki. A Stewart-tételt három háromszögre alkalmazzuk:

\begin{matrix} A B C Δ : (E B^{2} + \frac{e^{2}}{4}) e = a^{2} \frac{e}{2} + b^{2} \frac{e}{2}, \\ A C D Δ : (E D^{2} + \frac{e^{2}}{4}) e = c^{2} \frac{e}{2} + d^{2} \frac{e}{2}, \\ B E D Δ : (E F^{2} + \frac{f^{2}}{4}) f = E B^{2} \frac{f}{2} + E D^{2} \frac{f}{2} . \end{matrix}

A törtek eltávolítása és egyszerűsítés után lesz:

\begin{matrix} 4 \cdot E B^{2} + e^{2} = 2 a^{2} + 2 b^{2}, \\ 4 \cdot E D^{2} + e^{2} = 2 c^{2} + 2 d^{2}, \\ 8 \cdot E F^{2} + 2 f^{2} = 4 \cdot E B^{2} + 4 \cdot E D^{2} . \end{matrix}

E három egyenlet megfelelő tagjait összeadjuk:

\begin{matrix} 8 \cdot E F^{2} + 2 e^{2} + 2 f^{2} = 2 a^{2} + 2 b^{2} + 2 c^{2} + 2 d^{2}, \end{matrix}

ill.

\begin{matrix} 4 \cdot E F^{2} + e^{2} + f^{2} = a^{2} + b^{2} + c^{2} + d^{2} ... \end{matrix}

(III.)

Ámde a feltétel értelmében

\begin{matrix} e^{2} + f^{2} = a^{2} + b^{2} + c^{2} + d^{2}, \end{matrix}

így III.-ból

E F = 0

, de akkor a két felezőpont egybeesik. Azonban az olyan négyszög, amelynek átlói felezik egymást, parallelogramma, ennélfogva

A B C D

parallelogramma.
4. A Ptolemäus-tétel bizonyítása.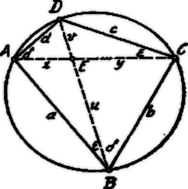

Jelöljük

A B C D

húrnégyszög átlóit:

A C = x + y = e

és

B D = u + v = f

, akkor

A B C Δ

-ben a Stewart-tétel értelmében:

\begin{matrix} (u^{2} + x y) e = a^{2} y + b^{2} x ... \end{matrix}

(IV.)

Azonban:

\begin{matrix} A B E Δ \sim D C E Δ : x y = u v, a y = u c; \\ A D E Δ \sim B C E Δ : b x = d u . \end{matrix}

Ezeket figyelembe véve IV.-ből lesz:

\begin{matrix} (u^{2} + u v) e = a u c + b d u . \end{matrix}

Osszunk

u

-val és helyettesítsünk

u + v = f

, akkor megkapjuk a Ptolemäus-tételt:

\begin{matrix} e f = a c + b d . \end{matrix}

A Ptolemäus tételnek ez a levezetése főleg azért előnyös, mert egyetlen egy segédvonalat sem kell megrajzolnunk.³

dr. Kresznerics Károly
Budapest

¹Matthew Stewart (olv. Sztyuört) (1717‐1785) skót matematikus, akinek tétele ,,Some general theorems of considerable use in the higher parts of Mafhematics'' c. munkájában, 1746-ban jelent meg.

²A tétel trigonometriai levezetését megtaláljuk Weber ‐ Wellstein: Encyklopädie der Elementar‐Mathematik II. k. 331. old.

³A Stewart-tétel sok alkalmazását találjuk M. C. Thiry: Applications remarquables du Théoréme de Stewart el Théorie du Barycentre 1891, továbbá a ,,Bulletin de mathématiques élémentaires'' 1895‐96. évf. (113‐118. old.) és 1903-4. évf. (50. old.).