Kezdőlap


Cím:	Sokszögekre vonatkozó szélső érték feladatokról
Szerző(k):	Fejes László (1936) [0-0]
Füzet:	1937/április, 229 - 232. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Jelentsen $K$ az alábbiakban egy csúcspontnélküli zárt konvex síkgörbét. Tekintsük a $K$ -ba írható legnagyobb területű háromszöget.^{$^{*}$} Ez a háromszög legjobban közelíti meg $K$ területét oly értelemben, hogy az eltérés $K$ és a háromszög területe között erre a legkisebb az összes $K$ -ba írható háromszögek közül.
Kérdés mármost, hogy ez a legjobban approximáló ‐ vagy mint mondani szokás extrém ‐ háromszög milyen tulajdonsággal bír?
Nem egyszerű feladat mindazon tulajdonságot megadni, amelyek egyértelműen meghatározzák a háromszöget; másszóval: megadni a szükséges és elégséges feltételét annak, hogy valamely $K$ -ba írt háromszög maximális területű legyen. Könnyű ezzel szemben erre egy igen jellemző, de pusztán szükséges feltételt találni, amelyet általánosabb alakban adunk meg:
A $K$ -ba írható legnagyobb területű $n$ -szög bármely csúcspontjában a $K$ -hoz húzott érintő párhuzamos a két szomszédos csúcsponton át fektetett szelővel.
Tegyük fel u. i., hogy valamely $K$ -ba írt $n$ -szög nem bír ezzel a tulajdonsággal. Hagyjuk ekkor változatlanul az $n$ -szög $n - 1$ csúcspontját, az $n$ -ediket azonban hozzuk a fent megjelölt helyzetbe. A sokszög területe ezzel nyílván növekedett.
Az alábbiakban hasonlóan fogunk eljárni. Jellemezni fogjuk az extrém sokszöget bizonyos tulajdonsággal. Nem vizsgáljuk azonban, hogy valamely polygon, mely ilyen tulajdonsággal bír, vajon extrém sokszög-e?
2. A $K$ köré írható legkisebb területű $n$ -szög minden oldalát a $K$ -val való érintési pontja felezi.
Ennek, valamint az ezt követő tételnek a bizonyításánál felhasználunk egy, az analízisben gyakran szereplő segédtételt:
Legyenek $φ (x)$ és $ψ (x)$ $x_{0}$ környezetében folytonos függvények. Ha most $φ {(x)}_{0} < ψ (x_{0})$ , akkor megadható egy pozitív $h$ szám, úgy, hogy $φ (x) < ψ (x)$ , valahányszor $| x - x_{0} | < h$ .

\begin{matrix} 1. ábra \end{matrix}

Vegyünk ezután tekintetbe egy polygont, melynek egyik

A B

oldalát az

O

érintési pont nem felezi:

\bar{A O} > \bar{O B}

. (1. ábra.) Válasszunk

A O

-on egy

C

pontot

O

-hoz oly közel, hogy

A C > C B

. A

C

-ből húzott érintőnek a szomszédos oldallal ill. annak meghosszabbításával való metszéspontja legyen

A'

ill.

B'

. Mivel

\bar{A' C}

ill.

\bar{C B'}

\bar{O C}

távolsággal folytonosan változik, választhatjuk segédtételünk alapján

C

-t úgy, hogy

\bar{A' C} > \bar{C B'}

legyen. Ekkor azonban területüket illetőleg:

C B B' Δ < C A A' Δ

.
Ha tehát

A B

-t a többi oldal érintési pontjainak változatlanul hagyása mellett

A' B'

-vel helyettesítjük, akkor az így előálló sokszög területe az eredetivel szemben csökken. U. i. az új sokszög területéből

C A A' Δ

kiesik, ellenben hozzájárul a

C B B' Δ

; a kiesés nagyobb, mint a növekedés.

\begin{matrix} 2. ábra \end{matrix}

1

.-ben a

K

-ba,

2

.-ben a

K

köré írt

n

-szögek közül vizsgáltuk azt, melyre a polygon és

K

közt lévő terület minimális. Most a polygonra semmi kikötést nem téve, fogjuk jellemezni azt az

n

-szöget, melyre ez a ,,területi eltérés'' (2. ábrán a vonalkázott síkrész területe) a lehető legkisebb.
A

K

-t terület szempontjából legjobban megközelítő

n

-szög minden oldalát saját felezőpontja és

K

-val való két metszéspontja négy egyenlő részre osztja.
Könnyen belátható, hogy az extrém polygon

K

-t, tételünknek megfelelően, valóban kétszer metszi. Tegyük tel pl., hogy valamelyik oldal teljes egészében

K

-n kívül van. Ezt az oldalt a vele párhuzamos érintővel helyettesítve, az eltérés csökken. Hasonlóan csökkenthető az eltérés, ha valamely oldal végpontjaival együtt

K

belsejében van. Nézzük most azt az esetet, amidőn valamely oldal egyik végpontja

K

-n kívül, a másik

K

-n belül van. Forgassuk el ezt az oldalt

K

-val való metszéspontja körül addig, amíg a belső végpont

K

-ra nem ér. Az eltérés ezáltal ismét csökkent.
Az az eset azonban, melynél valamely oldal

K

-t érinti, vagy végpontja

K

-n van, határesete annak, amelynél két metszéspont van. Erre (lényegtelen módosítással) az alábbi bizonyítást alkalmazhatjuk.

\begin{matrix} 3. ábra \end{matrix}

Legyen tehát

A B

valamely

n

-szög egyik oldala, melyre ‐ feltevésünkkel ellentétben ‐ pl.

\bar{A C} + \bar{D B} < \bar{C D}

, hol

C

és

D

A B

-nek

K

-val való metszéspontjai. (3. ábra.) Toljuk el ekkor

A B

-t magával párhuzamosan

h

távolsággal

A' B'

-be. Az új metszéspontok legyenek

C'

, ill.

D'

. Mivel

\bar{A' C'}

\bar{C' D'}

, valamint

\bar{D' B'}

h

-nak folytonos függvénye, választhatom

h

-t úgy, hogy

h > 0

, és

\bar{A' C'} + \bar{D' B'} < \bar{C' D'}

. Ezért:

\begin{matrix} \bar{A C} + \bar{D B} + \bar{A' C'} + \bar{D' B'} < \bar{C D} + \bar{C' D'} \end{matrix}

tehát

\begin{matrix} \frac{\bar{A C} + \bar{A' C'}}{2} h + \frac{\bar{D B} + \bar{D' B'}}{2} h < \frac{\bar{C D} + \bar{C' D'}}{2} h . \end{matrix}

Ha most az egyenesvonalú trapézek helyett a megfelelő vegyes vonalú trapézek területét vesszük, még inkább áll:

\begin{matrix} A C A' C' + D B B' D' < C D D' C' . \end{matrix}

Az eltolást alkalmas irányban végezve

A C A' C' + D B B' D'

a területi eltérés növekedését,

C D D' C'

a csökkenését jelenti. Ha tehát

\bar{A C} + \bar{D B} \neq \bar{C D}

, akkor az eltérés csökkenthető.

\begin{matrix} 4. ábra \end{matrix}

Tegyük fel mármost, hogy

\bar{A C} + \bar{D B} = \bar{C D}

, de ‐ a feltétellel ugyancsak ellentétben ‐ pl.

\bar{A C} < \bar{D B}

(4. ábra.). Az eltérést ebben az esetben

A B

-nek alkalmasan választott

O

pontja körüli elforgatásával kisebbíthetjük. Válasszuk

O

-t

A B

-n úgy, hogy

O A' A Δ = O B' B Δ

. A

K

görbe és a polygon közötti eltérés ezáltal egyrészt növekszik, másrészt csökken. Az elforgatást az ábrán megjelölt irányban végezve, a növekedés:

O D D' + A C A' C'

; a csökkenés:

O C' C + D B' B D

A' B'

-nek

A B

-hez elég közel való választásával az

O

pont tetszésszerinti közel juthat

A B

felezési pontjához. Választhatjuk tehát

O

-t úgy, hogy

O D < O C

, sőt ‐ ismét a folytonosságra hivatkozva ‐ úgy, hogy

O D D' < O C' C

. Ekkor azonban:

\begin{matrix} C' A' A C + O D D' < D' B' B D + O C C' \end{matrix}

ami éppen az eltérés kisebbedését jelenti. Az

\bar{A C} + \bar{D B} = \bar{C D}

és

\bar{A C} = \bar{D B}

feltételek viszont a tételben kimondott feltétellel ekvivalensek.
4. Nézzük ezután a kerület szempontjából legjobban approximáló polygonokat.
A

K

-ba írt legnagyobb kerületű

n

-szög bármelyik két szomszédos oldala közül egyik a másikának a szögpontjukban

K

-hoz húzott érintőre vonatkozó tükörképe.

\begin{matrix} 5. ábra \end{matrix}

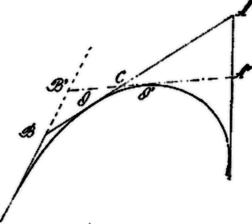
Legyen u. i.

A

B

C

rendre valamely

n

-szög három egymásután következő csúcspontja. (5. ábra.) Vegyük tekintetbe azt az ellipszist, melynek fókuszai

A

és

C

, és amely

K

-t az

\hat{A C}

íven érinti. Legyen az érintési pont

B'

A B'

és

B' C

egymással (az ellipszisre vonatkozó ismert tétel alapján) a fent megjelölt viszonyban vannak. Feltéve, hogy

B

nincs valamely érintési pontban (amikor is

B

az ellipszis belső pontja):

\begin{matrix} A B + B C < A B' + B' C, \end{matrix}

amivel állításunkat igazoltuk.
5. Foglalkozzunk végül a

K

köré írható legkisebb kerületű

n

-szöggel. Rajzoljuk meg az

n

-szög bármely oldalához azt az érintőkört, mely

K

-n kívül fekszik és amely egyúttal a két szomszédos oldal meghosszabbítását is érinti. Az extrém polygonnál ez a kör

K

-t érinti.

\begin{matrix} 6. ábra \end{matrix}

Világos mindenekelőtt, hogy az extrém polygon minden oldala érinti

K

-t. Ha azonban feltételünk valamely

P

polygonra nincs kielégítve, akkor könnyen szerkeszthető

P

-vel egyenlő kerületű polygon, melynek viszont nem minden oldala érinti

K

-t, jelöljük a tételben szereplő körnek az

A B

oldallal szomszédos oldalak meghosszabbításával való érintési pontjait

C

ill.

D

-vel (6. ábra). Ezen oldalak

K

-val való

E

és

F

érintési pontjait változatlanul hagyva, helyettesítjük

A B

-t a körnek oly

A' B'

érintőjével, mely

K

-t nem érinti. Nyilvánvaló, hogy ezáltal a polygon kerülete nem változott, mert

\begin{matrix} \bar{E A} + \bar{A B} + \bar{B F} = \bar{E A'} + \bar{A' B'} + \bar{B' F}; \end{matrix}

u. i. az egyenlőség mindkét oldala

= \bar{E C} + \bar{D F}

.
Ismételjük, hogy az itt tárgyalt feltételek nem elegendők az extrém polygonok meghatározására. Érdekes probléma azonban annak eldöntése, hogy e feltételek milyen speciális esetben definiálják egyértelműen az extrém sokszöget és hogy ebben az esetben az ,,eltérést'' a bizonyításban leírt módon állandóan csökkentve, az így előálló polygonsorozat konvergál-e? Ezáltal lehetséges volna u. i. az extrém polygont tetszés szerinti pontossággal megszerkeszteni.

Budapest, 1936.
Fejes László
IV. é. bölcsészhallgató

^{$^{*}$}A szélső érték exisztenciája ebben az esetben ‐ valamint a következőkben ‐ Weierstrassnak egy nevezetes tételéből folyik.